基于模型的非凸聚类算法

钟卓辉,陈黎飞,3

(1.福建师范大学计算机与网络空间安全学院,福建 福州 350117;2.数字福建环境监测物联网实验室,福建 福州 350117;3.福建省应用数学中心,福建 福州 350117)

1 引言

将一组数据划分成若干子集(每个子集为一个簇)的任务归为聚类的范畴,要求不同簇中的数据尽可能相异,而同一簇中的数据尽可能相似[1,2]。迄今,研究人员已提出多种聚类算法。这些聚类算法可粗略地划分为层次聚类、基于划分聚类、基于密度聚类、基于模型聚类以及其他聚类算法[1]。然而,在譬如医疗诊断等的许多科学领域,簇结构往往呈现非对称多峰等非凸特性,多数算法依赖于范数距离最小等原则,往往导致生成的簇倾向于具有凸状结构。因此,大多数传统的聚类算法在这类非凸簇或被称为非规则簇的聚类问题时功能受限[3]。针对该类挑战,研究人员提出了多种解决方法。现有的非凸聚类方法大致分为基于原始空间的方法[4-6]和基于空间变换[7-9]的方法。

第1类方法直接在原始空间内定义聚类算法,适用于非凸簇结构的问题。具有代表性的方法是基于密度的聚类,其原理是在原始欧氏空间中找到被空的或稀疏的区域分隔开的集中区域。譬如DBSCAN(Density-Based Spatial Clustering of Applications with Noise)[5],其以每个样本为中心在原始局部线性空间中,在事先指定邻域阈值参数ε的欧氏距离半径内计算样本的个数作为密度,基于密度可达距离的概念将样本点相连成簇。另外,Mean Shift[6,10]及其变体考虑一种更为鲁棒的连续性密度,通过核密度估计方法计算样本的密度。最新研究表明,密度峰值聚类DPC(Density Peak Clustering)[4]是Mean Shift的一种变步长的特殊变种[11]。

在这类方法中,随着维度d的增加,数据点在空间的分布变得越来越稀疏,此时基于一些常用的距离度量方法,如欧氏距离,数据点之间的距离将趋于相等,从而导致所谓的“差距趋零”现象。这种空间对象的稀疏分布特性同样会影响到譬如邻域阈值ε的概念,不适用于较高维的数据[12,13]。

第2类方法将原始空间中的数据进行空间变换,使得簇在原始空间中可能具有的非凸形状在新空间中接近于球形,然后在这个新空间中使用传统的K-Means[14]算法或其他经典算法进行聚类。代表算法包括谱聚类[7]、核聚类[8]和子空间聚类[9]等。Kernel-K-means[15]算法以核函数为桥梁进行空间映射,以黑盒方式对原始空间中样本的特征进行组合,放大数据之间的差异,使样本分布在新空间中变得规则。子空间聚类的基本思想是：使用一个随机的变换矩阵将原始数据的每个列向量投影到一个单位向量长度的低维空间,达到维度约简目的的同时可使簇的形状接近于规则的球形[16]。

另一方面,聚类分析作为一种描述性数据挖掘方法,数据聚类的目的应不仅限于揭示数据中潜在的簇结构,还需提供理解和产生这种簇结构的潜在机制[1,17],比如簇类的描述性模型。基于这种描述性模型的算法称为基于模型的聚类算法[18-20]。从统计学的角度,谱聚类和K-means[14]等都可以视作一种基于模型的方法。比如K-means所学习的模型实际上就是以方差等参数为常数的一类简化高斯混合模型[20]。

然而,这些方法都没有显式地构造数据背后的描述性统计模型。而这种描述性建模过程有利于充分发挥聚类分析的潜力,挖掘数据中重要信息。比如,可以应用一些统计方法,如最大似然估计等分析数据的分组,对生成的簇进行显式的统计刻画,为每个分量提供概率分布描述每个样本,提供关于样本-簇划分的概率向量等。另外,这样的模型还可用于聚类有效性问题的研究[12]。

当前,基于模型的方法应用于非凸簇聚类存在的困难有2个方面。首先,该方法本质上是将样本空间划分成K个Voronoi区域,决定了划分结果中的K个簇一定是凸集(球形或椭球)。其次,由于高维数据分布本质上是稀疏的,在这种情况下,这些源自多元高斯分布的样本在其“中心”附近的占比将迅速下降到0,产生所谓的“空空间现象”[21]。

本文提出一种基于模型的非凸聚类算法MNCC(Model-based method for Non-Convex Clustering),以弥补上述方法存在的缺陷。MNCC从不同密度极大值的覆盖区域导出簇的划分准则,从模型建立和优化2个方面实现基于模型的非凸聚类且无需事先给定簇的数目。本文主要工作有：

(1)提出了一个模型来描述非凸结构的簇。以非参数估计方法替代参数化分布,避免对总体分布的假定,直接以所有样本实例的函数定义总体数据混合形式的密度,并定义了样本权重和特征权重用于衡量样本和特征对密度函数的重要程度,以此建立模型。

(2)基于模型以最大化样本似然为目标推导优化目标函数,并提出一个期望最大化EM(Expectation Maximization)类型求解密度函数密度极大值的优化算法。通过概率描述簇,可以应用最大似然估计等统计方法推导模型参数的计算公式,用于优化目标函数。此外,簇的数目不需人为设定,而是在优化模型参数后根据密度极大值确定。

2 基于模型的非凸聚类

本节介绍一种非凸聚类的模型和聚类目标优化函数,并提出一种求解该目标函数的算法。给定数据集X={x1,x2,…,xi,…,xN},其中,N为数据样本点数目,任一D维数据样本点表示为xi=(xi1,xi2,…,xid,…,xiD)。给定N个对象,聚类算法将其划分为K个不相交的非空子集C1,…,Ck,…,CK,每个子集为一个簇,第k个簇Ck包含的样本点数记为nk。

2.1 高斯核密度混合模型

高斯混合是许多基于模型的聚类算法对数据分布模型做出的基本假设[22]。在这种情况下,数据点被认为来自各种(有限个)各自特定的高斯分布。采用这种有限混合模型的聚类需要一个假设,即每个簇对应于其簇内数据的概率密度函数都是单峰分布,使得每个混合成分能够捕获一个单独的峰值[23]。然而,在非凸聚类问题中,簇形状往往呈现多峰特性,这违背了传统有限混合模型的假设,无法有效地刻画非凸簇的形状。除此之外,由于维度灾难[11,21],高斯混合分布模型常用于描述低维空间中的簇类,并不适用于高维空间。一种与之不同的思路是,通过高斯核密度估计方法对数据进行非参数估计建模[24],借助众数概念将簇定义为总体概率密度函数的密度极大值所覆盖的区域[25]。首先给出基于高斯核密度估计的总体密度函数,如式(1)所示：

(1)

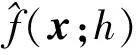
(2)

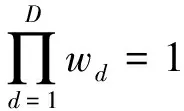
(3)

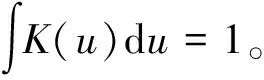
(4)

(5)

将式(1)与式(5)相比可知,后者借助核函数K(·)对原始数据进行“核化”,在非线性概率空间中考虑了特征之间的联系,且在映射后的概率空间中通过权重wd进行了特征选择,同时还以参数αj考虑了不同样本点对总体密度函数的贡献程度。这种概率空间的映射与核聚类或谱聚类方法是不同的,其能够通过显式模型进行描述。当αj=1/N,j=1,2,…,N且wd=1/D,d=1,2,…,D时,式(5)退化为一般的核密度估计式。显然,式(1)是所提概率模型的一种特殊情况。

2.2 聚类准测

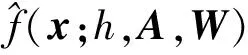
(6)

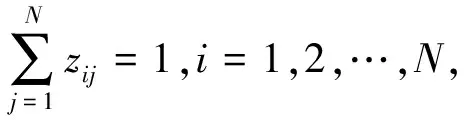
(7)

由Jensen不等式[1]可知：

(8)

(9)

可以看到,式(8)的右边是一个带约束的非线性优化问题。记上述关于wd,aj,zij的约束条件分别如式(10)～式(12)所示：

(10)

(11)

(12)

应用拉格朗日乘子法,结合上述定义,则优化目标如式(13)所示：

J(X,h,Θ,Z)≥J1(X,h,Θ,Z)

(13)

J1(X,h,Θ,Z)=

(14)

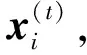
(15)

h(t+1),Θ(t+1),X(t+1)=

(16)

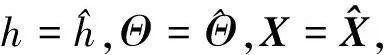
(17)

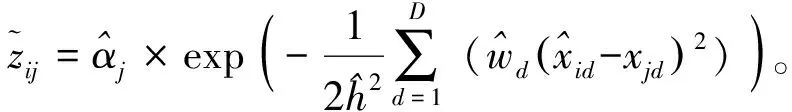
证明当F(x,x,h,αj,W)/zij为常数β时有式(18)：

(18)

式(18)同时乘以zij并关于j进行求和有：

(19)

将式(19)代入式(18)有：

(20)

联立式(20)和式(9)进行约简后得式(17)。

当zij满足式(17)时,F(xi,xj,h,αj,W)/zij为常数,此时关于式(13)的等号成立,对目标函数J1(·)的优化即是对原始对数似然的优化。下面证明式(16)为J1(·)关于隐变量Z的局部最优解。根据式(16),可以定义N个独立的子优化目标函数,如式(21)所示：

Ji(zi,ξi)=

(21)

(22)

联立式(22)和式(9)可得式(17)。

□

3 MCNN聚类算法

本节给出MCNN算法的具体描述。所提算法的优化步骤分别对应E-step和M-step 2个局部优化问题,对目标函数的每组参数进行局部优化。第2节已经给出了E-step关于Z的局部优化问题的具体细节。在M-step步骤中将式(16)的最优化问题分解为3个分别关于样本点集合X、带宽h和权重参数集合Θ的局部优化问题,具体依据是以下3个定理。

(23)

(24)

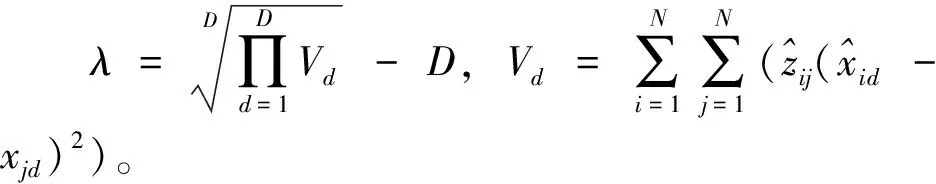
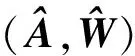
(25)

(26)

联立式(25)和式(26),可分别得到式(23)和式(24)。

□

(27)

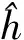
(28)

□

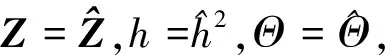
(29)

(30)

联立式(29)与式(12)可得式(30)。

□

根据上述参数的求解方法,当任意样本点不再改变时,所有样本点收敛于某个局部区域的极大值。从收敛后的所有数据点中提取不相同的数据点作为密度极大值的集合M={mk|k=1,2,…,K},这样簇的数量也同时能够自动确定,即为集合M的长度K,即密度极大值的数目。样本点关于簇的划分遵循如式(31)所示的规则：

(31)

在实际训练过程中,需要给定一个阈值ε,当一对样本间的距离小于这个阈值时,认为其属于同一个密度极大值点。综上所述,MCNN算法具体过程如算法1所示。

算法1 MNCC输入：X,并记为X(0)。输出：聚类划分{C1,C2,…,Ck}。初始化： 令t为迭代次数,初始化t=0; 令Z={zij=1/N|i,j=1,2,…,N},并记为Z(0); 令W={wd=1/D|d=1,2,…,D},并记为W(0);repeat： 根据式(26)更新带宽h并记为h(t+1); 根据式(22)和式(23)更新权重向量W和先验A,并记其集合为Θ(t+1); 根据式(17)更新隐变量Z并记为Z(t+1); 根据式(28)更新样本点X并记为X(t+1); 更新迭代次数t：t=t+1;Until X(t+1)-X(t)<10e-5 从X(t+1)中提取密度极大值的集合M。遍历X,根据式(30)将样本xi划分至Ck中。

从算法结构可知每一次迭代过程的时间复杂度为O(N2D),假设算法迭代次数为T,则该算法时间复杂度为O(N2DT)。算法在每一次迭代过程中提高目标函数值,又因为似然函数有界,因此在有限的迭代次数下算法是收敛的。关于该算法的严格收敛性证明可参照关于EM算法的收敛性证明[27]。

4 实验与结果分析

本节评估了所提出的MCNN聚类算法在人工数据集和实际数据集上的性能,并通过实验将 MCNN与一些经典的或最新的聚类算法进行比较。

4.1 实验设置

实验选择了5种聚类算法进行对比,包括DBSCAN[5]、DPC[4]、Kernel-K-means[15]、SCSM (Spectral Clustering for Single and Multi-view data)[28]和GMCM(Gaussian Mixture Copula Models)[29]。其中,DBSCAN以样本点的密度可达概念划分不同的簇,为邻域密度聚类中最具代表的算法之一;DPC利用数据的局部密度以及相对距离属性快速确定聚类中心,已经成为密度聚类的研究热点之一;Kernel-K-means在K-means的基础上引入了核函数,实现原始数据空间非线性映射;SCSM是一种最近提出的谱聚类算法,通过提出的自适应密度感知内核增强共享共同最近邻居的点之间的相似性,并以此构造相似矩阵。Kernel-K-means与SCSM代表了基于空间变换的2种非凸聚类主流算法。实验还选择了最近提出的GMCM算法,其使用高斯混合 Copula-meta 模型进行聚类,与本文算法的相似点在于二者都是基于模型的聚类算法。所有对比算法都需要人为设置参数值。在本文实验中,对这些参数使用了最常见的设置或推荐值。不同算法的参数设置情况如下所示。

对于DBSCAN的密集区域所需最小点个数MinPts和邻域半径ε,根据文献的推荐设置MinPts的搜索范围为MP={mp|D+1≤mp≤2D,mp∈N};对于给定的mp,以关于该mp的k-distance图的值域作为ε的搜索范围。DPC算法通过计算特定距离矩阵的距离截止值dc(即截断距离),使平均相邻率(距离截止值内的点数)落在提供的范围之内。需要的截断距离参数dc由所有点的邻居数量的平均值占数据点总量的百分比nr确定。根据文献推荐,nr的取值为0.2%,0.4%,0.6%,1%,2%,4%,6%,8%,因此本文以0.1%为步长在[0.2%,8%]进行搜索。对于Kernel-K-means,其核函数的参数σ设置搜索范围为[0,1],搜索的步长设置为0.01。对于SCSM中特征分解近邻数等参数及GMCM的参数,使用原文献中推荐的默认值。此外,Kernel-K-means和GMCM算法需要设置簇数K,实验中使用真实簇数目作为输入。

为了验证MCNN聚类算法的性能,实验采用人工数据集和真实数据集进行测试。由于已知各数据集类别标签,本文选择外部聚类评价指标：规范化互信息熵NMI(Normalized Mutual Information)[30]和F-Score[20]评估算法的聚类性能,其计算公式分别如式(32)和式(33)所示：

(32)

(33)

其中,nl为数据集第l类的样本数,Rk,l为聚类结果中簇ck与第l类匹配的样本数,Rel,k和Pel,k分别为第l类与聚类结果中簇ck相比较的准确率和召回率。NMI和F-Score的值越大,表示聚类结果质量越好。

各对比算法均通过设置参数组进行多次实验获取参数最优值,以取得NMI值最大的参数作为最优参数。对于具有随机性的算法,随机初始化参数后进行50次实验,并选择获得NMI值最大的参数作为最优参数。为了实验的公平性,所有非随机性的算法均取其最优参数下的聚类结果。具有随机性的算法取其最优参数下100次实验中对应最大NMI值的聚类结果。

4.2 人工数据集实验

为了测试MNCC算法的可行性,本节在4个著名的非凸簇人工数据集上进行测试,包括Jain、Aggregation、D31和Four-lines,数据维度均为二维,这有助于对聚类结果进行可视化展示。表1给出了各数据集的具体信息。

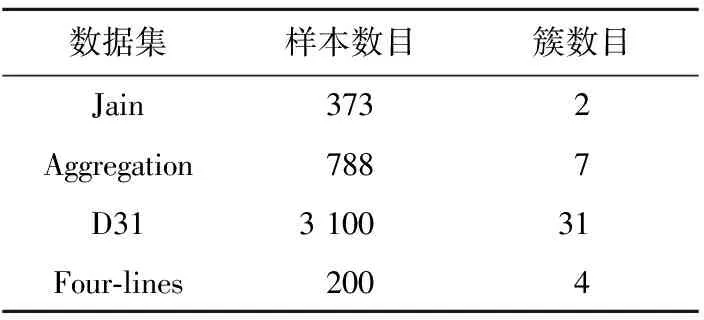
Table 1 Information of artificial datasets

图1给出了4个数据集的初始样本分布情况,其中Jain(图1a)数据集包含了2类密度差较大的非凸状簇,在原始数据空间中无法线性可分,呈现月牙状分布;Aggregation(图1b)包含了7个形状大小不一的簇,其密度较为均匀,但簇间存在各种异常点和干扰点;D31(图1c)包含了31个紧密相连的簇,且簇间有明显的重叠现象;Four-lines(图1d)包含了4个呈现条状的簇,且簇的大小和密度不一。

Figure 1 Initial distribution of samples in four artificial datasets图1 4个人工数据集的样本初始分布情况

图2展示了本文提出的MNCC聚类算法在4个人工数据集上的聚类可视化结果。可以看出,MNCC算法在上述4个不同类型的人工数据集上表现优异,其中在Jain和Four-lines上聚类结果完全正确;在Aggregation和D31数据集上聚类结果几乎完全正确。部分对比算法的最优参数如表2所示。各对比算法与MNCC算法的聚类性能对比情况如表3所示,表内粗体数字为各数据集上最高的指标值。

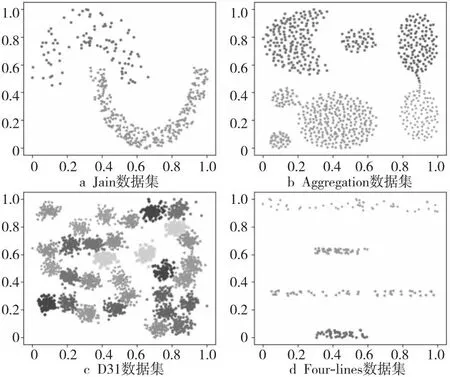
Figure 2 Clustering results of MNCC algorithm on four artificial datasets图2 MNCC算法在4个人工数据集上的聚类结果

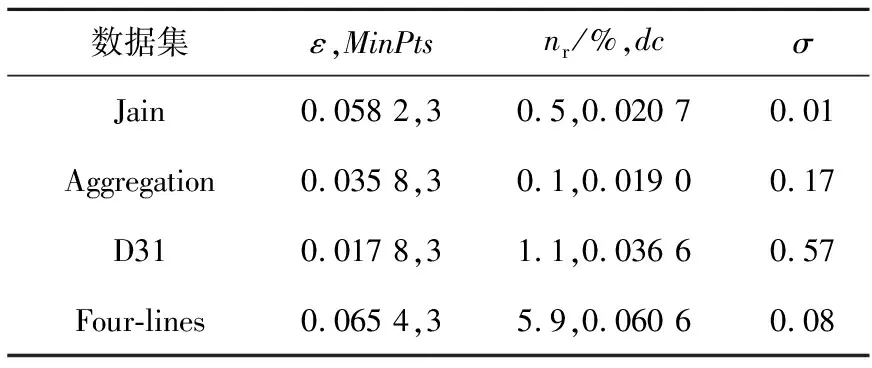
Table 2 Optimal parameters of some comparative algorithms on four artificial datasets

Table 3 Performance comparison of six algorithms on four artificial datasets

总体而言,MNCC在4个数据集上获得了相对于对比算法更高的聚类质量,表明本文算法在处理非凸聚类问题时具有很高的可行性。除此之外,GMCM在Jain和Four-lines数据集上的NMI值最低,侧面反映了传统的基于模型的聚类方法无法胜任非凸聚类问题。

4.3 真实数据集实验

为进一步测试 MCNN 算法的聚类性能,本节还在真实数据集上进行测试。实验采用来自加州大学欧文分校UCI(University of California Irvine)数据库(http：//Archiveics.uci.edu/ml/datasets.html)的6个真实数据集,其详细信息如表4所示。

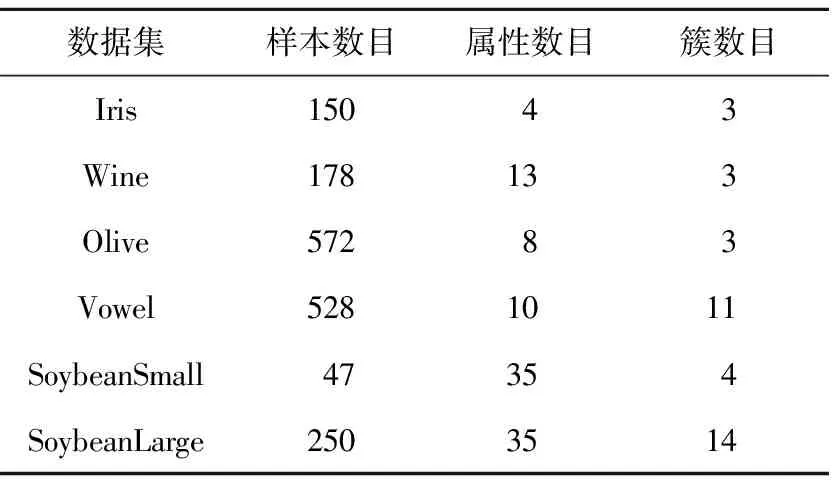
Table 4 Information of six UCI real-world datasets

表5展示了部分对比算法的最优参数,表6给出了各算法在真实数据集上的聚类性能对比情况。

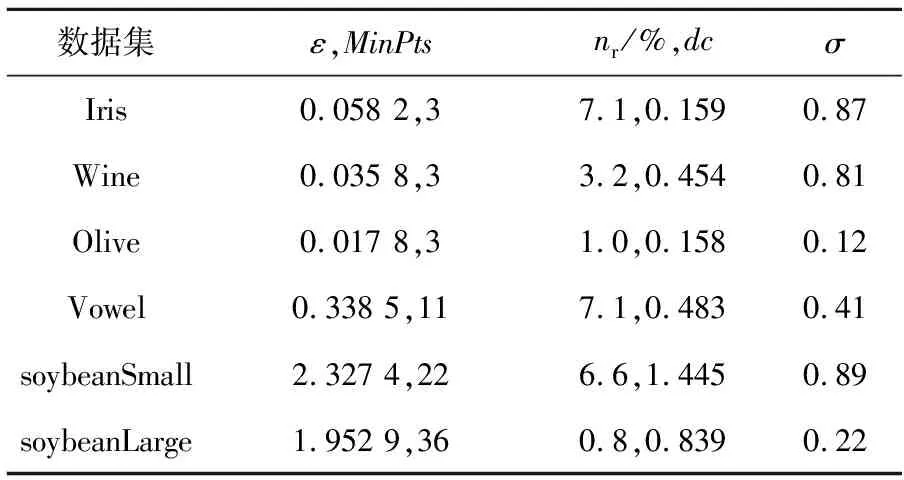
Table 5 Optimal parameters of some algorithms on 6 real-world datasets

Table 6 Performance comparison of six algorithms on six real datasets

从表6可知,与对比算法相比,MCNN算法在除Wine外的其余真实数据集上均获得了NMI最大的聚类性能,特别是在Soybean-Small和Olive数据集上聚类结果完全正确。值得注意的是,在类别数较高和相对高维的SoybeanLarge数据集上,MNCC的NMI和F-Score值高于其他对比算法的甚多,说明了所提算法具有良好的适应性。

Figure 3 Feature weight distribution obtained by MNCC on five real datasets图3 MNCC获得的5个真实数据集上的特征权重分布

以SoybeanSmall数据集为例,从MCNN算法的一次聚类结果中提取特征权重信息作进一步分析。图4给出了数据空间中特征权重的对数尺度直方图,其中y轴上的值是权重在特定范围内的对数。权重小于0.1的属性数量为27,这表明只有8个属性(A2,A12,A23,A24,A26,A27,A28,A35)对聚类效果有较大贡献,因此以0.1为阈值提取原始特征集合的子集,通过新构造的特征子集(soybean_8)测试MCNN算法和5种对比算法的性能。表7给出了有关算法的最优参数,表8给出了算法在SoybeanSmall上的原始特征集合和新特征子集上的聚类对比情况。

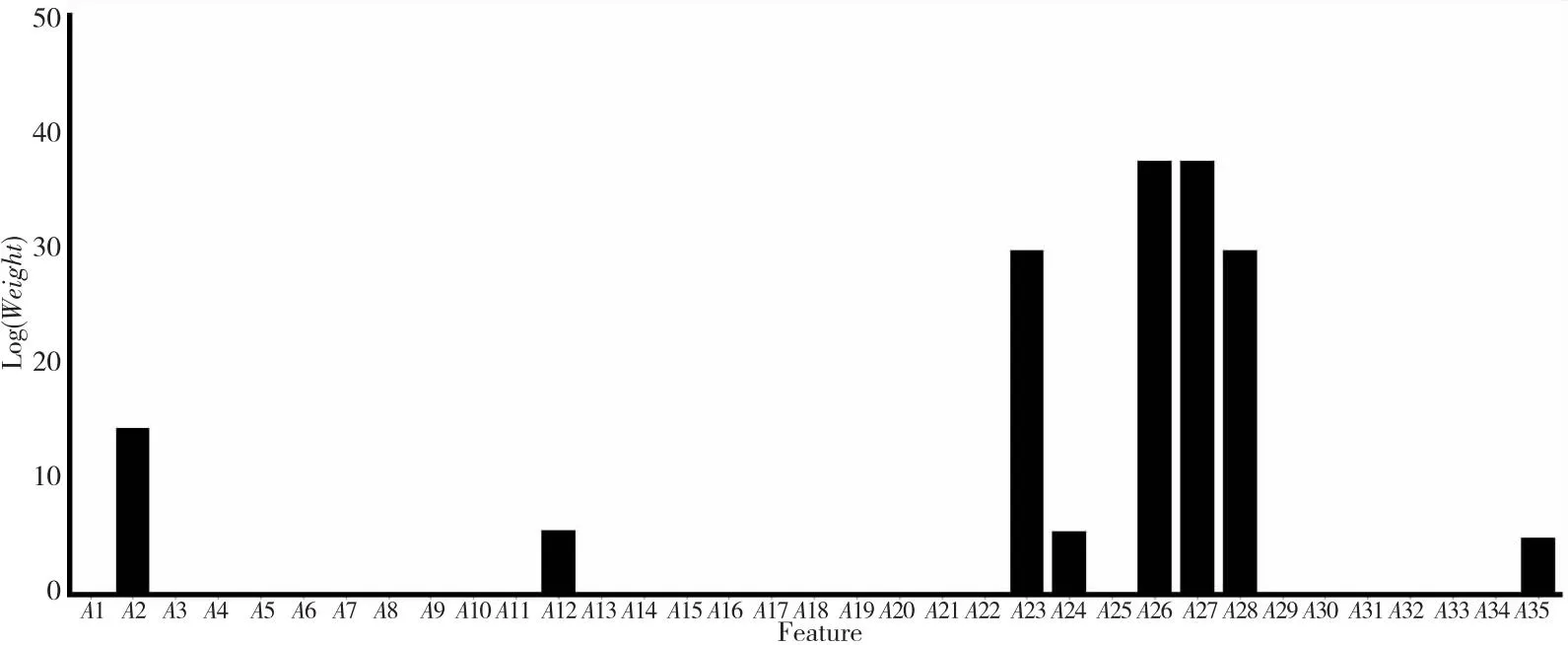
Figure 4 Feature weight distribution obtained by MCNN on Soybeansmall dataset图4 MCNN获得的Soybeansmall数据集上的特征权重分布

Table 7 Optimal parameters of some algorithms on soybean_8

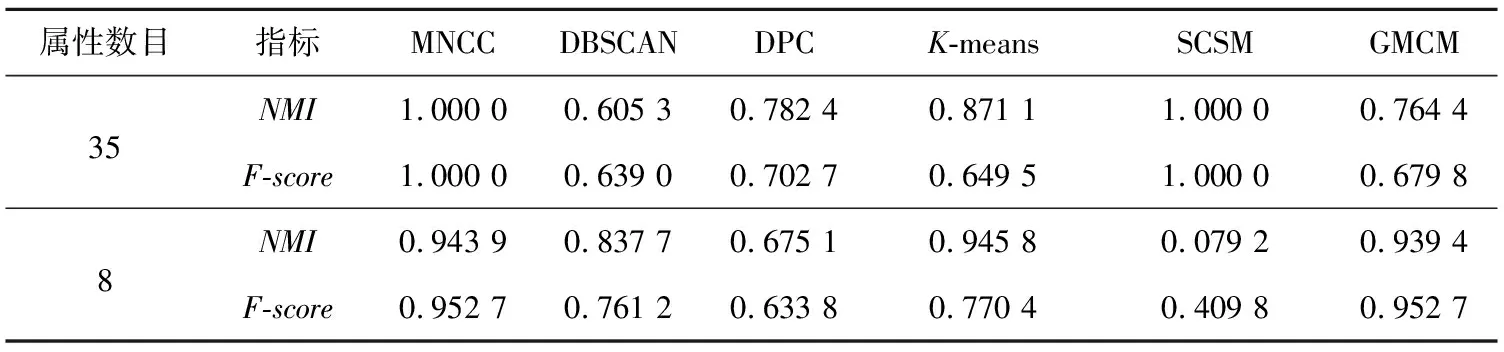
Table 8 Performance comparison of six algorithms on Soybean and its feature subsets

表8的聚类结果表明,大多数算法基于MCNN挖掘的特征子集能够有效提高聚类性能,从而提高了高维数据上非凸聚类问题的聚类性能。

5 结束语

针对非规则簇的聚类问题,本文提出了一种基于模型的非凸聚类算法MNCC。所提算法在概率框架下进行,给出了一种簇类的描述性模型,这是其他非凸聚类算法所不具备的。所提算法基于高斯核密度估计,构造了一种基于核密度估计的混合模型,在非线性概率空间中挖掘属性间关系,同时进行属性重要程度的估计,然后基于上述模型,提出了一种期望最大化的爬山优化方法,进而提出了新的聚类算法MNCC。在人工数据集和真实数据集上的实验结果表明,与现有的其他非凸聚类算法相比,MNCC算法有效提高了聚类质量。