面向Stacking算法的差分隐私保护研究

董燕灵,张淑芬,4,徐精诚,王豪石

(1.华北理工大学理学院,河北 唐山 063210;2.河北省数据科学与应用重点实验室,河北 唐山 063210;3.唐山市数据科学重点实验室,河北 唐山 063210;4.唐山市大数据安全与智能计算重点实验室,河北 唐山 063210)

1 引言

随着科技的发展,从互联网到移动设备,从社交媒体到物联网,产生了越来越多信息和数据。许多机构和企业使用集成学习技术对收集到的信息进行分析,以获取有用的知识来便利人们的生活。但是,隐私泄露和隐私侵犯的问题也随之而来,人们对隐私保护问题越来越关注。为了保护个人隐私,越来越多的研究人员开始研究关于隐私保护的理论和技术,并且提出了一系列的解决方案。

当前应用于集成学习的隐私保护技术主要有加密和扰动2种。加密常通过同态加密[1,2]、哈希技术[3,4]等来对训练数据进行加密,以阻止他人窃取敏感信息。扰动通常使用差分隐私技术[5-7]来实现,采用拉普拉斯机制[8]、指数机制[9]或高斯机制[10]对数据添加噪声,防止包括攻击者在内的第三方从发布的数据集中提取有价值的信息。相较于传统的加密技术,差分隐私不需要对数据进行额外的加密处理,且支持对多种不同类型的数据进行隐私保护,如数值型数据、文本型数据和图像型数据等,还具有高度的可伸缩性,可以根据实际需要添加额外的隐私约束,从而更好地保护数据。

差分隐私技术已经被扩展应用于许多集成学习算法,如随机森林[11-14]、Adaboost[15-18]和提升树[19,20]等,但单一同质的集成学习算法可能很难满足同时达到有效隐私保护和较好预测性能的要求。因此,本文提出将异质Stacking算法与差分隐私技术相结合的算法。Stacking算法是一种强大的集成学习算法,被广泛应用于文本分类[21]、图像分类[22]、生物医学[23]等各种重要领域,与单一的同质集成学习算法相比,其组合了多个不同的弱学习器预测结果来提高模型的精度。当前将差分隐私技术与Stacking算法结合起来的相关研究较少。Salem等人[24]提出了一种基于模型泛化的Model Stacking方法来进行隐私保护。Yao等人[25]提出了一种通过Stacking算法来增强隐私保护逻辑回归PLR(Privacy-preserving Logistic Regression) 的方法。李帅等人[26]提出了一种DPC-Stacking(Differential Privacy protected Clustering of Stacking)算法来解决单一聚类算法在差分隐私保护下准确性和安全性不足的问题。在这些已有的将差分隐私技术与Stacking算法相结合的研究中,主要有2个缺陷：一是隐私预算分配方案不具有广泛的应用性,不能适用于由任意学习器构成的Stacking算法;二是对训练集重复添加差分隐私保护,使得数据的可用性降低。

基于此,本文设计了一种基于Stacking元学习器的隐私预算分配方案,将此方案与Stacking算法结合,提出一种基于差分隐私的DPStacking(Differential Privacy of Stacking)算法,只需对训练集添加一次差分隐私保护,提高数据集的可用性,在保证算法准确率的同时,提高Stacking算法在模型训练过程中的安全性。具体来说,本文的主要工作如下所示：

(1)为有效解决单一同质集成学习算法对噪声敏感的问题,提出一种基于差分隐私保护的DPStacking算法,在保护数据隐私的同时,兼顾模型的可用性及分类结果的准确性。

(2)对于元学习器输入的不同构成体,分别通过皮尔逊相关系数和差分隐私并行组合的特性设计不同的隐私预算分配方案。

(3)通过理论分析证明了DPStacking算法满足ε-差分隐私保护,并在真实数据集上进行实验,将DPStacking算法与其他隐私保护集成学习算法进行对比,评估DPStacking算法的有效性。

2 差分隐私保护技术

差分隐私保护技术是一种通过在数据之间添加一定数量噪声来掩盖数据的真实信息,使攻击者无法通过差分攻击来获得有效信息,从而达到保护数据隐私效果的技术。

2.1 差分隐私的定义及相关概念

定义1(差分隐私[5-7]) 设有随机算法W,PW为W所有可能的输出构成的集合。对于任意2个具有相同属性结构,只存在一条记录差的数据集D和D′以及PW的任何子集SW,若式(1)成立,则称算法W提供了ε-差分隐私保护。

Pr[W(D)∈SW]≤eεPr[W(D′)∈SW]

(1)

其中,参数ε为隐私保护预算,表示数据隐私的保护程度,ε越小,隐私保护能力越强;Pr[·]表示发生某一事件的概率。

定义2(全局敏感度[8]) 对于2个具有相同属性结构,只存在一条记录差的数据集D和D′,查询函数f(·)最大的变化为全局敏感度Δf。Δf的计算如式(2)所示：

Δf=maxD,D′‖f(D)-f(D′)‖1

(2)

定义3(并行组合[8]) 给定任意n个互不相交的数据集Di,1≤i≤n,假设有n个随机算法Ki满足εi-差分隐私,则由{Ki(Di)}(1≤i≤n)组合后的算法满足max(εi)-差分隐私。

2.2 实现机制

拉普拉斯机制是差分隐私保护技术中的一种实现机制,其核心思想是在释放数据的同时,向每个数据添加一个有噪声的随机偏移量,添加的随机噪声服从拉普拉斯分布。设尺度参数为λ,位置参数为0,则该拉普拉斯分布为Laplace(λ),其概率密度函数如式(3)所示：

(3)

定义4(拉普拉斯机制[8]) 给定数据集D和隐私预算ε,设有查询函数f(D),其敏感度为Δf,那么随机算法W(D)=f(D)+Y提供ε-差分隐私保护。其中Y～Laplace(Δf/ε)为随机噪声,服从尺度参数为Δf/ε的拉普拉斯分布。拉普拉斯机制的整体思想是以一定的概率输出异常值。

3 基于差分隐私的DPStacking算法

本文提出一种DPStacking算法,通过将差分隐私应用于Stacking算法中,在保证模型精度的前提下,降低模型训练过程中数据泄露的风险.

本文使用的主要符号如表1所示。

Table 1 Primary symbols

Table 2 Information of experimental datasets

3.1 Stacking算法

Stacking算法是一种利用K-折交叉验证的集成学习算法,它将多个基学习器的结果进行组合,以期得到更好的预测性能。该算法通过将训练集分成K个不同的子集,每次只使用其中一个子集作为测试集,其余K-1个子集作为训练集,这样可以获得K个不同的基学习器模型。然后,将这K个基学习器模型的输出作为新的特征,以此建立新的预测模型,实现最终的预测。基于K-Fold交叉验证的Stacking生成算法如算法1所示。图1为2个基学习器的3-折交叉验证Stacking模型。

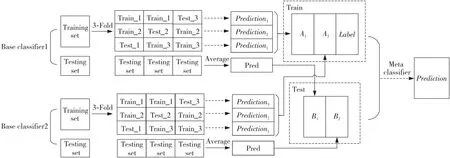
Figure 1 3-Fold verify Stacking model图1 3-折交叉验证Stacking模型

3.2 DPStacking算法

在Stacking算法的实际应用过程中,隐私泄露的风险主要来自于第1层模型的训练,当第1层模型中的数据包含敏感信息时,如果其中单个学习器在集成过程中泄漏了个人隐私,那么第2层模型的训练集和测试集就可能受到影响,从而暴露个人隐私。本文提出为第2层模型的训练集和测试集添加差分隐私保护的方法。具体来说,针对元学习器的训练集和测试集,分别设计了2种不同的隐私预算分配方案,并引入拉普拉斯机制来进行扰动。

由于元学习器训练集A是由基学习器的预测结果At和训练集D的标签值yi组成,因此本文根据At与yi的相关性,提出一种基于皮尔逊相关系数的隐私预算分配方式。

定义5(皮尔逊相关系数[27,28]) 皮尔逊相关系数是一种统计指标,用来量化2个变量之间的线性相关性。2个变量间的皮尔逊相关系数ρx,y的计算如式(4)所示：

(4)

其中,cov(x,y)表示协方差,E(x)表示x的期望值,σx表示x的标准差。ρx,y∈[-1,1],ρx,y越接近1,表示2个变量越正相关;越接近-1,表示2个变量越负相关;而越接近0,表示2个变量间没有显著的线性关系。式(4)为2个变量间的总体相关系数,那么2个样本的皮尔逊相关系数rx,y的计算如式(5)所示：

(5)

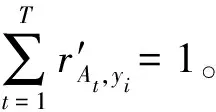
(6)

由于At与yi互不相交,根据差分隐私并行组合的特点,分配给yi的隐私预算即为元学习器训练集的隐私预算,向yi添加拉普拉斯噪声,如式(7)所示：

(7)

基于元学习器训练集的隐私预算分配算法如算法2所示。

算法2 基于元学习器训练集的隐私预算分配算法输入：元学习器的训练集A,隐私预算ε。输出：A。 步骤1 计算At与yi间的皮尔逊相关系数rAt,yi;步骤2 对rAt,yi进行归一化,r′At,yi=rAt,yi∑Tt=1rAt,yi;步骤3 计算分配给At的隐私预算;步骤4 for t=1 to T：步骤5 为At添加拉普拉斯噪声,得到At;步骤6 end for步骤7 为yi添加拉普拉斯噪声,得到yi;步骤8 A={ai1,ai2,…,aiT,yi}ni=1。

对于元学习器测试集B={B1,B2,…,BT},它是由互不相交的子集Bt组成。假设元学习测试集的总隐私预算为ε,则分配给Bt的隐私预算无需再平均分配,而是直接同等于测试集B的隐私预算,因此向Bt添加拉普拉斯噪声,如式(8)所示：

(8)

基于元学习器测试集的隐私预算分配算法和DPStacking生成算法分别如算法3和算法4所示。

算法3 基于元学习器测试集的隐私预算分配算法输入：元学习器的测试集B={B1,B2,…,BT},隐私预算ε。输出：B。 步骤1 for t=1 to T：步骤2 为Bt添加拉普拉斯噪声,得到Bt;步骤3 end for步骤4 B={B1,B2,…,BT}。

3.3 算法分析

3.3.1 时间复杂度分析

假设训练集样本个数n,特征数量为d,折叠数为K,基学习器个数为T,算法2和算法3的时间复杂度为：O(Tdn),算法4的时间复杂度为：O(TKdn)。

3.3.2 隐私性分析

定理1算法2和算法3满足ε-差分隐私。

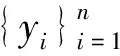
max(εr′A1,yi,εr′A2,yi,…,εr′AT,yi)≤

max(εr′At,yi,ε)≤ε

(9)

设算法3中总的隐私预算为ε,分配给Bt的隐私预算为ε。由于元学习器测试集B={B1,B2,…,BT}是由互不相交的子集Bt组成,于是根据差分隐私并行组合的特点,式(10)可满足：

max(ε)=ε

(10)

因此,算法2和算法3满足ε-差分隐私。

□

定理2算法4满足ε-差分隐私。

证明设算法4中总的隐私预算为ε,有相邻数据集D和D′,W(D)和W(D′)表示数据集D和D′执行算法1的输出结果,f(D)和f(D′)表示数据集D和D′执行算法4的输出结果,f(D)=W(D)+Y,f(D′)=W(D′)+Y,其中Y～Laplace(Δf/ε)服从尺度参数为Δf/ε的拉普拉斯分布,则式(11)满足：

(11)

因此,算法4满足ε-差分隐私。

□

4 实验及结果分析

4.1 实验数据

实验所选数据集来源于公开的 UCI(University of California Irvine)机器学习数据库中的Adult数据集和Bank Marketing数据集,具体信息如表 2 所示。

通过对Adult数据集进行分析发现,属性native-country为非美国籍的样本数仅占总样本数的 16%,因此剔除非美国籍的样本,仅选取美国籍的样本记录进行训练和测试。此外,属性fnlwgt的值是通过对和当前样本具有相似人口特征的人进行加权统计而得出的人口总数,该属性对本文的分析价值较低,也将该属性删除。本文选取数据集的 70%作为训练集,30%作为测试集,在2个数据集上分别进行实验。

4.2 实验结果与分析

在相同参数下,每组实验重复运行50次后取平均值作为算法的平均分类准确率。其中基学习器选择RF(Random Forest)算法、Adaboost算法和XGBoost算法。由于Stacking算法在采用K-Fold交叉验证的方式将基学习器的输出用于元学习器的训练时,已经使用了复杂的非线性变换,Stacking为了防止过拟合,通常选取简单的学习器作为它的元学习器。本文的元学习器选择逻辑回归算法,折叠数K=5,ε=0.1,0.3,0.5,0.7,1,3,5。

从表3可以发现,在不添加差分隐私保护时,异质集成Stacking算法的分类准确率比RF算法、Adaboost算法和XGBoost算法的高,这说明Stacking算法可以改善模型的泛化能力,使其具有更好的预测能力和较高的可用性。

Table 3 Classification accuracies of Stacking and other integrated learning algorithms

本文将DPStacking算法与DiffRFs(Random Forest under Differential privacy)算法[13]、DP-AdaBoost(Differential Privacy of AdaBoost)算法[17]、DPXGB(Differential Privacy XGBoost)算法[19]进行对比,实验结果如图2所示。从图2可以看出,DPStacking算法和DP-AdaBoost算法在ε≤0.5时分类准确率较其他算法的偏低。这是因为DiffRFs算法和DPXGB算法采用往基决策树内部加噪的方式,而DPStacking算法和DP- AdaBoost算法采用对数据集加噪声的方式。具体来说,DPStacking算法通过对元学习器的训练集和测试集加噪声,DP-AdaBoost算法通过对基学习器的预测结果类标签加噪声,当ε较小时,添加的噪声对数据集的破坏较大,数据可用性较差,因此DPStacking算法和DP-AdaBoost算法的分类准确率较低;而当ε变大时,噪声对数据集的影响逐渐减小,数据集的可用性提高,因此DPStacking算法和DP-AdaBoost算法在ε≤0.5时,随着ε的变大,分类准确率上升幅度较大。此外,当ε>0.5时,DPStacking算法的分类准确率比其他差分隐私集成学习算法的高,这符合Stacking算法异质集成的预测能力优于同质集成算法的特点。

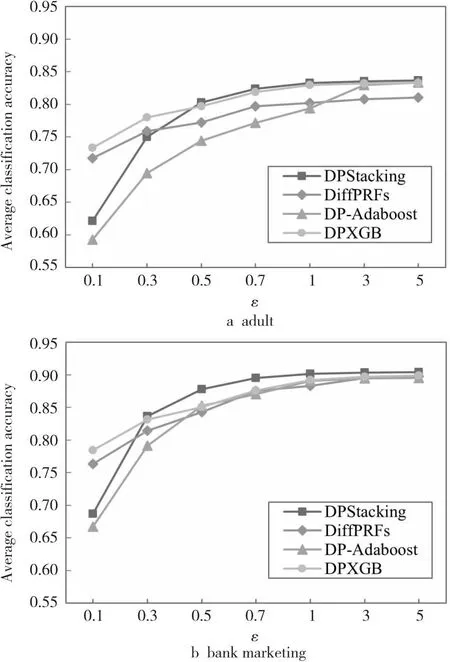
Figure 2 Classification accuracies comparison of DPStacking algorithm and other differential privacy integrated learning algorithms图2 DPStacking算法与其他差分隐私集成学习算法的分类准确率比较

计算当ε=1时DPStacking与其他差分隐私集成学习算法的精确度PR(Precision Rate)、召回率RR(Recall Rate)和F1-score,结果如图3所示。其中,精确度指模型预测为正的样本中实际为正的样本所占的比例;召回率为实际为正的样本中被模型预测为正的比例;F1-score表示精确率和召回率的调和平均,可以综合表现模型的性能。从图3可知,DPStacking算法的平均精确度、平均召回率、平均F1-score均高于其他差分隐私集成算法的,这说明DPStacking算法在保护隐私的前提下具有更优的性能。

Figure 3 Results comparison of each index图3 各指标比较结果

本文还对ε=1时DPStacking算法每次分类结果的准确率进行了记录,结果如图4所示。对于Adult数据集而言,平均分类准确率为83.37%;第21次的运行结果最低,对应的分类准确率为83.1%;第19次的运行最高,对应的分类准确率为83.92%。Bank数据集上的平均分类准确率为90.18%;第3次的运行结果最低,对应的分类准确率为89.98%;第40次的运行最高,对应的分类准确率为90.38%;并且不难发现50次运行的结果都不相同,这是由于拉普拉斯噪声是随机的,它以一定的概率输出异常值来扰乱数据。

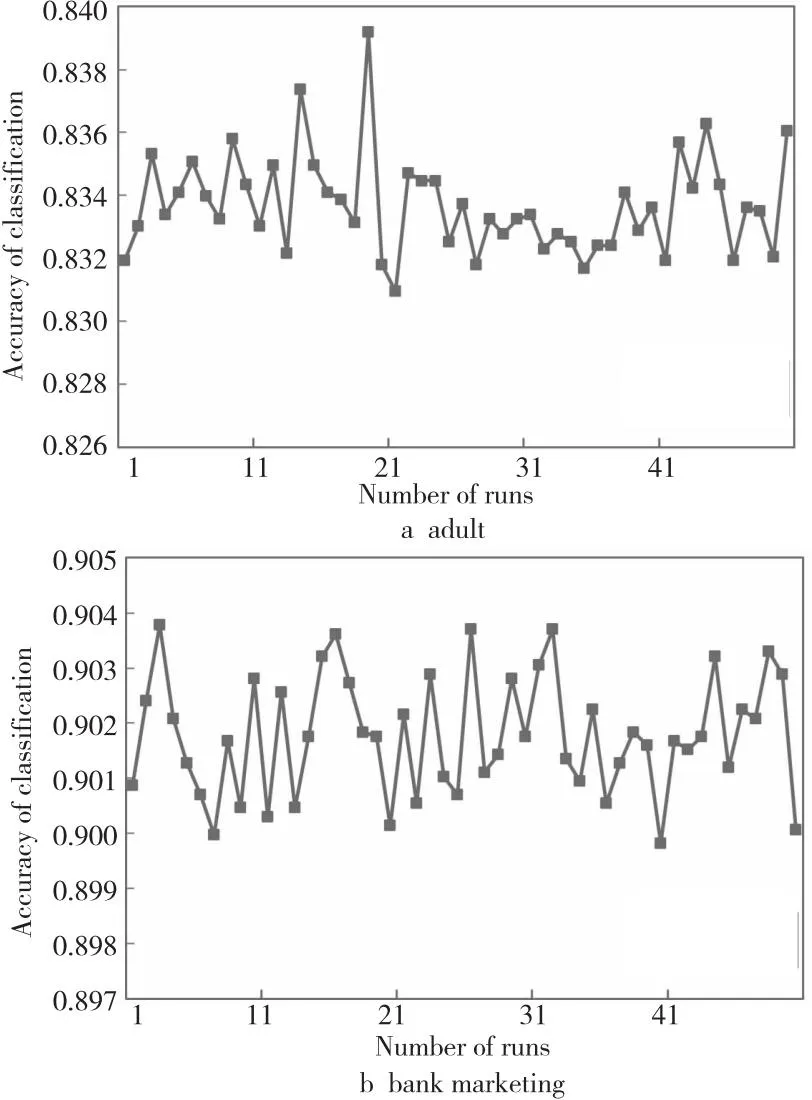
Figure 4 Classification accuracies of DPStacking algorithm when ε=1图4 ε=1时DPStacking算法分类准确率

综上,DPStacking算法与其他差分隐私集成学习算法相比,DPStacking算法具有显著的优势,尤其是在隐私预算较高的情况下,它的各项指标均高于其他差分隐私集成算法的,在保证模型可用性的基础上对数据信息进行了隐私保护,模型预测精度也明显提高。

5 结束语

本文提出了一种基于差分隐私的DPStacking算法,与现有的差分隐私集成学习相比,本文所提算法具有以下优势：

(1)针对Stacking算法中基学习器的输出用于元学习器训练的特点,对元学习器输入构成体设计了不同的隐私预算分配方案。通过计算元学习器训练集内不同子集间的皮尔逊相关系数,为元学习器训练集内的不同子集分配不同的隐私预算,根据差分隐私并行组合的特性为元学习器测试集内的子集分配隐私预算。

(2)提出的隐私预算分配方案具有较强的应用性和灵活性,能够应用于多种不同的基学习器和元学习器构成的Stacking算法。

(3)用理论证明了DPStacking算法符合ε-差分隐私保护,用实验验证了该算法相较于同质差分隐私集成学习算法,在拥有更好的预测性能的同时,仍能有效保护用户隐私,并较好地解决了单一同质集成学习算法对噪声较敏感的问题,具有较高的实用价值。

下一步,将考虑如何在隐私保护和数据可用性之间找到最佳平衡。