辛体系下含对称破缺因素动力学系统的近似守恒律

胡伟鹏, 林志华, 邓子辰

(1.西安理工大学 土木建筑工程学院,西安 710048;2.香港城市大学 建筑学及土木工程学系,香港 999077;3.西北工业大学 力学与土木建筑学院,西安 710072)

1 引 言

冯康先生[1]在1984年双微国际会议上针对有限维Hamilton系统提出的辛算法,打破了提高数值精度作为数值分析方法研究的唯一目标这一局限性,开启了计算数学的另一扇大门,冯康先生也因此荣获1997年国家自然科学一等奖,并被菲尔兹奖得主丘成桐先生誉为“中国数学的三驾马车”之一。此后,各种构造Hamilton系统辛离散格式的途径相继报道[2],极大地促进了辛几何算法在计算数学领域的应用。

将辛体系引入弹性力学分析[3,4],并发展经典力学的辛求解体系[5,6],是钟万勰先生团队在计算力学领域开创性的研究工作之一。为了更好地表述连续变形系统(无限维系统)的辛结构,以及在动力学演化过程中的局部能量/动量随时间的演化和在空间的流动规律,文献[7,8]分别从变分原理和Legendre变换出发,发现了无限维Hamilton系统的时空联合辛结构,即多辛结构,并在多辛几何框架下,给出了无限维Hamilton系统局部能量和局部动量守恒律的显式数学表述,这些守恒律在无限维Hamilton系统数值分析中的重要性[9,10]已经逐渐得到学术界认可。

辛/多辛结构源自于理想数学物理模型的对称性[11],在其数值解的几何结构分析中扮演着重要角色。然而,完美的辛/多辛结构在实际的力学系统中不存在,因为工程师设计的力学系统是需要与外界交换能量的,即需要对外做功或者接受外界对其做功,无论系统中的非保守广义力是确定性的还是随机的。同时,力学系统本身也存在各种各样的不对称性,如结构不对称和载荷不对称等。随着现代力学的发展,力学系统参数可能不再是恒定的,具体体现在结构构型可变及材料参数时变等方面。上述动力学对称破缺的出现,破坏了理想数学物理模型的对称性,也破坏了系统大量的守恒律。针对无限维弱耗散Hamilton动力学系统,Hu等[12-15]基于多辛几何理论,发展了广义多辛分析方法,并在此基础上建立了动力学对称破缺因素与系统局部能量耗散之间的映射关系[16,17]。

本文在上述研究成果基础上,在辛体系下讨论含对称破缺的动力学系统的近似守恒律,为辛方法应用于非保守动力学系统的数值分析奠定数学基础。

2 有限维随机激励Hamilton系统的近似守恒律

一切忽略耗散效应的有限维动力学系统,均可以表述为下述Hamilton正则形式

(1)

式中q∈Rn为描述质点运动的广义坐标列向量,p∈Rn为对应的对偶向量,H(q,p)为系统总能量,即Hamilton函数。若令z=(q,p)T为系统的状态向量,则Hamilton正则形式(1)可进一步写成紧凑形式为

(2)

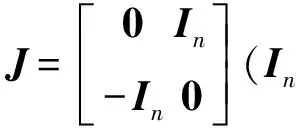
(3)

此外,Hamilton函数的全微分为

(4)

式(4)表明,有限维Hamilton系统的总能量不随时间演化,为一个严格的守恒量。

对于n维非线性随机动力学系统的柯西问题[18]

P(t0)=p

Q(t0)=q

(5)

若采用随机平均法,固然可以得到随机动力学系统(5)的一些特殊的近似解析解,但是并不能得到其诸如辛结构和修正的能量守恒律等本质属性。其中,wr(t)为相互独立的维纳过程,∘为Stratonovich积。

基于辛几何理论,系统(5)的辛结构可表述为

dP∧dQ=dp∧dq

(6)

也就是说,对于随机激励有限维Hamilton系统,辛结构依然存在。

3 含对称破缺因素的无限维动力学系统的近似守恒律

在Bridges[7]建立的多辛几何框架体系下,对于依赖于时间、空间n维的保守Hamilton连续系统,可以写成多辛对称形式为

(z∈Rd)

(7)

式中M,Ki∈Rd×d(i=1,2,…,n)为反对称常数矩阵,S∶Rd→R为光滑的Hamilton函数,z=z(t,x1,x2,…xn)为状态向量。

并且已经证明,多辛对称形式(7)必然精确满足如下三种守恒律。

(1) 多辛守恒律

(8)

式中ω=dz∧Mdz,κi=dz∧Kidz(i=1,2,…,n)。

(2) 局部能量守恒律

(9)

(3)xm(m=1,2,…,n)方向的局部动量守恒律

(10)

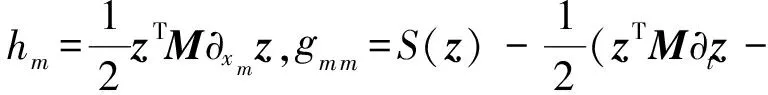
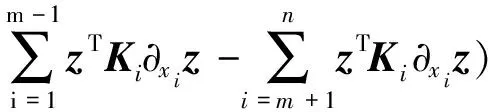
如前所述,实际工程中并不存在保守的Hamilton系统,即动力学对称破缺因素必定存在于力学系统中,如阻尼耗散、外部激励、结构/材料参数可变和系统参数随机或激励随机等。因此,本文分别讨论几种含对称破缺因素的无限维动力学系统的(近似)守恒律。

3.1 无限维耗散动力学系统的近似守恒律

对于含有阻尼耗散的无限维动力学系统,亦可通过多辛降阶方法将其写成近似对称形式为

(z∈Rd)

(11)

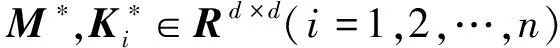
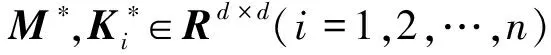
(12)

定义反对称矩阵M和Ki

(13)

(14)

则近似对称形式(11)可以改写为

(z∈Rd)

(15)

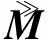
(16)

依照Bridges[7]建立的多辛积分理论,定义修正的能量密度为

(17)

和修正的能量通量为

(i=1,2,…,n)

(18)

则有

(19)

即得到近似对称形式(15)的修正局部能量守恒律

(20)

即近似对称形式(15)的局部能量误差为

同理,定义

(i=1,2,…,n)

(21)

(22)

同样得到近似对称形式(15)的修正局部动量守恒律

(23)

即近似对称形式(15)的局部动量误差为

对于下述几种对称破缺情况,本文只讨论其局部能量误差(即局部能量耗散)。

3.2 无限维变参数动力学系统的局部能量耗散

如果在多辛对称形式(7)中,矩阵方程的系数矩阵显式依赖于空间坐标和(或)时间坐标,

M=M(x1,x2,…,xn,t)=-[M(x1,x2,…,xn,t)]T

Ki=Ki(x1,x2,…,xn,t)=-[Ki(x1,x2,…,xn,t)]T

则修正的能量密度为

修正的能量通量为

能量通量的偏微分计算如下

(24)

则无限维变参数动力学系统的局部能量耗散表述为

〈∂t[Ki(x1,x2,…,xn,t)]∂xiz,z〉}

(25)

3.3 Hamilton函数显式时空依赖的无限维动力学系统的局部能量耗散

无论是施加于力学系统的外界激励还是控制,大都显式依赖于空间坐标和时间坐标,在这种情形下,无限维动力学系统(7)的Hamilton函数将显式依赖于时间坐标和空间坐标,即S=S(z,x1,x2,…,xn,t)。

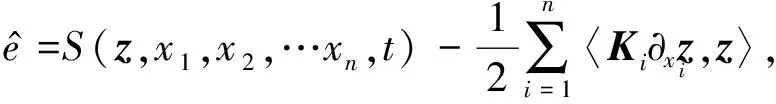
Δe=∂tS(z,x1,x2,…xn,t)/∂t+

(26)

3.4 无限维随机激励动力学系统的局部能量耗散

与已有针对白噪声激励下的无限维动力学系统不同,本节考虑受一般随机激励的无限维动力学系统,其一般矩阵形式可以表述为

(z∈Rd)

(27)

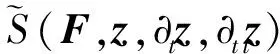
(28)

(29)

(30)

对于随机位移作用于结构边界的情形,系统局部能量耗散取决于结构边界性质。当边界条件不允许沿着随机位移方向的位移时,随机位移不会引起局部能量耗散。否则,随机位移就会引起局部能量耗散。限于随机位移的一般性,在此无法给出统一的局部能量耗散表达式。

4 算 例

为了说明上述结果在动力学系统分析中的应用,本节以柔性阻尼梁振动问题为例,说明阻尼耗散这一对称破缺因素对柔性梁振动系统的多辛结构残差和局部动量耗散的影响。

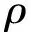
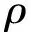
(31)

∂xz=zS(z)

(32)

式(32)的广义多辛守恒律为

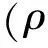
-cd(∂tu)∧du

(33)

定义式(33)的右端项为多辛结构残差,即Δ=-cd(∂tu)∧du。

式(32)的局部动量耗散为

(34)

采用Preissmann离散方法离散一阶近似对称形式(32)并消去中间变量,同时离散多辛结构残差和局部动量耗散,得到与Preissmann离散格式等价的广义多辛格式,以及每一时间步的最大绝对多辛结构残差和最大绝对局部动量耗散值

(35)

(36)

(37)

式中 Δt和Δx分别为时间步长和空间步长,式(36)的外积∧运算展开为

u(0,t)=u(l,t)=0

(38)

采用差分格式(35)模拟柔性梁的振动过程,记录梁振动过程中每一时间步最大绝对多辛结构残差和最大绝对局部动量耗散值如图1所示。

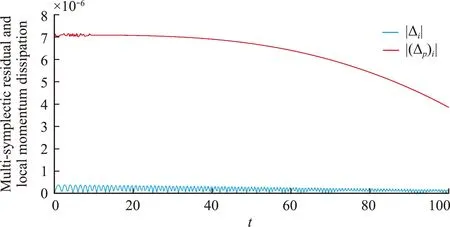
图1 最大绝对多辛结构残差与局部动量耗散

上述算例仅用以说明在实际问题中,如何采用保结构数值算法再现第3节给出的动力学对称破缺因素与系统近似守恒律之间的映射关系。因此,柔性梁振动过程的数值结果不再在本部分给出。

5 结 论

物理力学系统的对称性与守恒律存在一一映射关系,受这一结论启发,本文在辛体系下讨论含有动力学对称破缺因素动力学系统的近似守恒律。针对随机激励下的有限维Hamilton系统,得到了其辛结构;分别针对无限维耗散动力学系统、无限维变参数动力学系统、Hamilton函数显式时空依赖的无限维动力学系统和无限维随机激励动力学系统,详细讨论了对称破缺因素引起的局部动量耗散问题,为含有对称破缺因素的动力学系统的保辛算法设计提供理论依据。