电驱动海洋绞车自动排缆控制系统建模与仿真

2024-02-27刘晓进赵延明敬明洋

机械工程师 2024年2期

刘晓进，赵延明，敬明洋

（湖南科技大学信息与电气工程学院，湖南湘潭 411201）

0 引言

随着不可再生资源的不断消耗，世界各国纷纷聚焦深地深海来缓解资源供需矛盾[1-2]，海洋绞车是海洋资源勘探与开发装备布放、回收的关键船舶甲板设备[3]，但是，在复杂多变海况、工况条件等影响下，绞车时常出现乱缆（空槽、咬缆、背缆）、夹缆现象[4-5]，从而导致海洋装备收放作业停顿，甚至失败；而且乱缆、夹缆引发相互挤压容易引起缆绳磨损，甚至断裂[6-7]，致使海洋装备丢失。因此，如何解决绞车排缆故障，提高排缆质量，对确保海洋装备收放作业安全可靠至关重要。

绞车自动排缆是实现绞车安全可靠收放的关键技术，引起了国内外学者广泛关注，并在排缆机构结构、排缆方式及排缆控制方法等方面展开了大量的研究。张明松等[8]设计一种新型绞车滚筒钢丝绳自动强排装置，采用双向牙嵌式离合器结合纯机械结构驱动丝杆正反转动实现自动往复排绳功能。刘继芳等[9]利用机械传动控制机构使自动排线绞车实现绞线速率自动调节、绞线盘带动动力电缆上升下降。邓智勇等[10]采用纯机械式独立自动排缆装置实现绞车中脐带缆的整机排布及换层，实现了脐带缆绞车的自动排缆与作业装备的安全收放。上述文献采取的机械式强排缆方式，由于工作过程中机构之间摩擦磨损，机械传动比随之改变，而在排缆过程中排缆机构本身不能进行自动调节，随着工作时间的推移，其排缆效果会越来越差。为了克服机械式强排缆的不足，黄良沛等[11]运用矢量控制和SVPWM调制原理建立排缆控制系统模型，并设计基于模糊PID控制器的海洋绞车排缆系统，克服了PID控制抗干扰能力较差的弱点，分析了不同海浪工况下排缆响应，一定程度降低了受负载扰动、系统参数变化等不确定因素对排缆的影响。Kang等[12]针对不同缆径推导出丝杆速度与卷筒速度关系，进行绞车排缆速度控制系统建模，并运用智能PID算法进行排缆控制，确保了不同缆径的缆绳在卷筒上有序排列。孔繁增[13]采用两个绝对式编码器检测储缆卷筒、排缆丝杠的转速，并将储缆卷筒与排缆机构间的匹配关系转化为两个编码器所产生的脉冲总数间的匹配关系，比较两个脉冲总数来调节丝杠电动机的转速，实现自动排缆。

上述文献采取的电控式排缆方式, 通过卷筒转速与丝杠转速的关系表达式，匹配卷筒与丝杆的运动实现自动排缆，但由于海洋环境恶劣、检测存在干扰及系统滞后性等原因，很难实现自动精确排缆。为了克服运用卷筒转速与丝杆转速的关系自动排缆的不足，陈琦等[14]在缆绳进入导向轮的入口处安装偏角检测装置，通过检测缆绳偏角，设计自动排缆增量PID控制器，根据缆绳偏角控制液压马达驱动器实现自动排缆，保证缆绳在收放过程中与导向轮保持零偏角。

综上所述，无论是机械式强排缆方式，还是电控式排缆方式，实质上均是通过匹配卷筒与排缆丝杆的运动实现自动排缆。海洋绞车运行过程中受复杂多变海况、工况条件等影响，机械式强排缆方式以固定的传动比来匹配，无法消除外部干扰，易出现乱缆、夹缆现象；而电控式排缆方式没有综合考虑外部干扰因素并建立排缆机构数学模型，而是采取适当控制算法来提高系统抗干扰和响应能力，在浅海作业放出缆绳较短的情况下能取得一定排缆效果，但很难保证深海作业时的排缆质量。因此，本文以电驱动海洋绞车排缆系统为研究对象，综合考虑海浪、负载、缆绳、摩擦等因素，通过缆绳张力引入外部干扰，建立起电驱动海洋绞车自动排缆控制系统数学模型，仿真分析各因素对丝杆转速的影响，为电驱动海洋绞车自动排缆同步控制提供理论基础。

1 电驱动海洋绞车排缆系统结构与工作原理

电驱动海洋绞车自动排缆系统由伺服电动机、伺服驱动器、减速器、丝杆、导缆轮、行程开关、丝杆编码器组成，如图1所示，伺服驱动器驱动伺服电动机正反转，通过减速器带动丝杆旋转，实现导缆轮在丝杆上往返运动，运动到卷筒两端（即排满/收回一层缆）触发行程开关换向，丝杆每旋转一圈，导缆轮相应平移一个丝杆导程。采用6台交流变频电动机通过减速箱驱动卷筒旋转，卷筒正转实现作业装备布放，反转实现作业装备回收，卷筒每旋转一圈，放出/缠绕一股缆绳。采用“卷筒旋转一圈导缆轮沿卷筒轴向方向平移一个缆径位移量”原理匹配卷筒与丝杆的转速，实现有序排缆。

2 电驱动海洋绞车排缆控制系统建模

为了厘清海洋作业环境下各因素对电驱动海洋绞车排缆的影响，综合考虑海浪、负载、缆绳、摩擦等因素，对电驱动海洋绞车排缆系统进行建模，其框架图如图2所示，由于海浪和海流引起母船上下起伏运动，且作业装备与海水耦合，致使缆绳张力变化，并通过缆绳作用至导缆轮上，引起导缆轮与丝杆之间螺纹的正压力变化，从而改变导缆轮对丝杆的阻力矩，将引起绞车排缆系统数学模型参数变化。因此，将外部干扰引入到绞车排缆系统数学模型中，能更真实反映出各因素对丝杆转速的影响。排缆控制系统具体建模如下。

图2 电驱动海洋绞车排缆系统框架图

2.1 丝杆给定转速数学模型

海洋绞车匀速布放/回收作业装备，卷筒旋转不断放出/缠绕缆绳，丝杆旋转带动导缆轮沿卷筒轴向平移运动，当卷筒旋转一圈，导缆轮平移一个缆径位移量，就可实现有序排缆，当卷筒放出/缠绕满一层缆绳，丝杆将换向旋转，带动导缆轮反向平移，进行下一层排缆。因此，丝杆给定转速与作业装备收放速度之间存在图3所示的关系，设作业装备收放速度为v0，则卷筒给定转速n0为

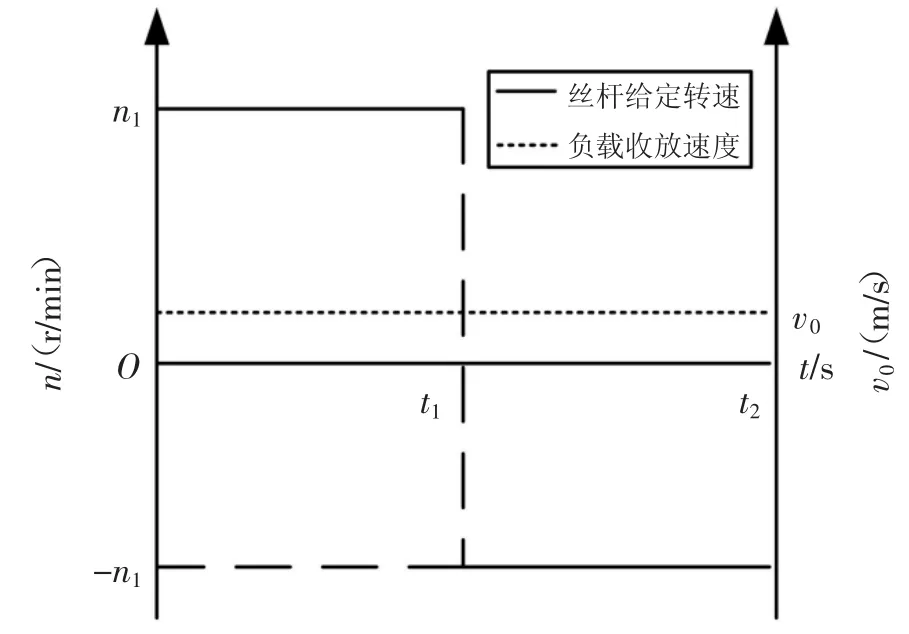
图3 丝杆给定转速与作业装备收放速度关系

式中，r为卷筒等效半径。

丝杆给定转速n1为

式中：D为缆绳直径，S为丝杆导程。

2.2 丝杆给定转速转换系数

在控制程序中，将丝杆给定转速转换成伺服驱动器控制电压信号Un，其转换系数Kn1为

2.3 排缆伺服驱动系统数学模型

排缆伺服驱动系统采用速度闭环反馈控制，通过比较丝杆转速与丝杆给定转速，控制伺服驱动器驱动伺服电动机，经减速器带动丝杆旋转，致使导缆轮沿卷筒轴向平移，实现与卷筒同步运动进行有序排缆，其系统结构图如图4所示。

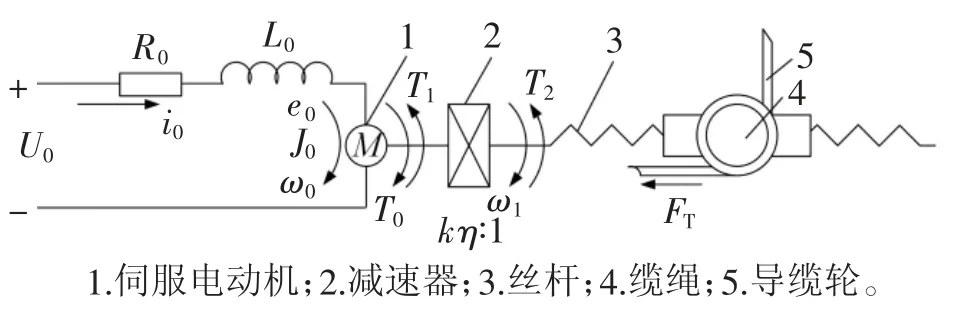
图4 排缆伺服驱动系统结构图

2.3.1 伺服驱动器数学模型

将伺服驱动器视为比例放大环节，其比例系数KU为

式中：U0为伺服电动机输入电压；Uk为伺服驱动器输入电压，Uk=Un-U2；U2为丝杆编码器输出电压信号。

2.3.2 伺服电动机数学模型

根据基尔霍夫定律，伺服电动机电枢回路的电势平衡的微分方程为

式中：R0为电枢回路电阻，L0为电枢回路电感，i0为电枢电流，e0为伺服电动机反电动势。

根据楞次定律，反电动势应当满足以下关系式：

式中：k0为丝杆伺服电动机的反电动势常数，ω0为伺服电动机轴的角速度。

根据安培定律，电枢电流i0与驱动力矩T0的关系式为

式中：k1为丝杆伺服电动机的转矩常数。

根据牛顿第二定律，丝杆伺服电动机轴上的转矩平衡方程方程为

式中：J0为伺服电动机转子转动惯量，μ0为伺服电动机轴承摩擦因数，T0为伺服电动机的电磁转矩，T1为伺服电动机的阻力矩。

2.3.3 减速器数学模型

伺服电动机轴通过减速器与丝杆轴进行连接，可以将减速器的传递函数看成是一个比例环节，减速器传动比k为

式中：ω1为丝杆旋转的角速度，rad/s；η为减速器的传动效率。

丝杆转速n2为

伺服电动机的阻力矩T1与丝杆驱动力矩T2之间关系为

2.3.4 丝杆运动数学模型

根据牛顿第二定律，丝杆轴上的转矩平衡方程方程为

式中：J1为丝杆转动惯量，T3为导缆轮对丝杆的阻力矩。

丝杆与导缆轮之间通过螺纹连接，丝杆在转动过程中驱动导缆轮平移运动，缆绳穿过导缆轮实现排缆，运行过程中缆绳张力通过导缆轮作用于丝杆与导缆轮之间的螺纹接触面上，其阻力矩为[15]

式中：FT为缆绳张力，D4为丝杆直径，μ1为丝杆与导缆轮之间螺纹摩擦因数。

而缆绳张力为

式中：m为负载等效质量，m1为作业装备质量，m2为放出缆绳质量，y¨为作业装备加速度。

2.4 丝杆编码器数学模型

丝杆编码器用来测量丝杆转速并将丝杆转速信号转换成电压信号，可以将其等效成比例环节，其比例系数Kn2为

式中：U2为丝杆编码器输出电压，n2为丝杆转速。

结合卷筒系统已有数学模型[16]，并对式（1）～式（15）进行相应的拉普拉斯变换，建立电驱动海洋绞车排缆系统数学模型，其框图如图5所示。

图5 电驱动海洋绞车排缆系统数学模型框图

图5中，根据参考文献[16]，母船升沉位移的数学模型为

式中：λ为海浪升沉位移与波高的比值，H为波高，T为海洋升沉运动周期。

变频电动机到卷筒的传递函数为

式中：p为电动机极对数，R2为转子绕组的相电阻，S′为转差率，N为线圈匝数，Kw为绕组系数，Φm为每极磁通量，R1为定子绕组的相电阻，X1为定子每相绕组的漏电抗，X2为转子每相绕组的漏电抗，J为转动部分折算到电动机轴上的总转动惯量，m为等效负载质量，r为卷筒半径，i为传动箱传动比。

作业装备运动位移到卷筒转角传递函数为

式中：C为海水阻尼系数，K为缆绳弹性刚度系数。

作业装备运动位移到母船升沉运动位移的传递函数为

3 仿真与分析

以某台海洋绞车为算例，运用建立的数学模型，分析不同参数对丝杆转速特性的影响。现给出绞车设计参数、排缆机构相关参数分别如表1、表2所示。

表2 排缆机构参数表

为了分析电驱动绞车排缆系统各参数对丝杆转速的影响，更有效实现海洋绞车自动排缆同步控制，针对图5所示建立的排缆系统数学模型，进行仿真分析，相关参数如表1、表2所示，现取作业装备质量为3000 kg，其回收速度为2 m/s，缆绳直径为32 mm，缆绳回收长度为3500 m，海浪等级为4级中浪，伺服电动机轴承摩擦因数（以下简称轴承摩擦因数）为0.04，丝杆与导缆轮之间螺纹摩擦因数（以下简称螺纹摩擦因数）为0.08，并在Simulink环境中建立电驱动绞车排缆系统仿真模型，对应仿真结果如图6所示。

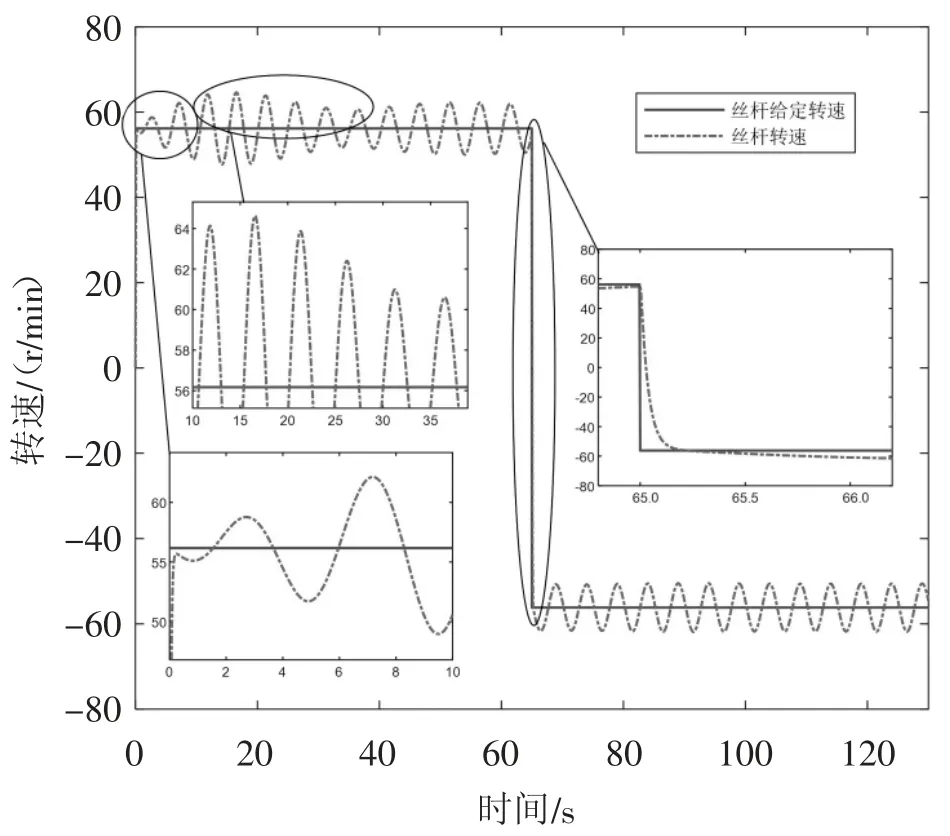
图6 电驱动海洋绞车排缆系统仿真结果

从图7可知，在前几个周期内丝杆转速幅度由小变大，然后趋于恒定，这主要是由于海洋绞车在回收作业装备过程中，作业装备在深海作业，受到母船升沉运动影响，还受到海水对作业装备浮力作用，其缆绳张力较小，由式（13）可知，丝杆所受阻力矩较小，因此在前2个周期内丝杆转速幅值较小，此时卷筒处于启动阶段；然后随着作业装备继续往上运动，卷筒进入缠绕阶段，缆绳张力增大，同时因母船升沉受到海水耦合作用力增大，丝杆所受阻力矩随之增大，因此在接着的3个周期内，丝杆转速幅值增大；当作业装备达到给定速度后，缆绳伸长量逐渐减小，缆绳张力减小，丝杆所受阻力矩略有减小并变化趋于稳定，丝杆转速幅值略有减少，其变化趋于稳定；直至回收一层缆绳，卷筒进入换层阶段，丝杆转速反向进入下一层缆绳，但作业装备仍往回收，卷筒转速方向不变，装备仅受到海水耦合作用力，丝杆所受阻力矩变化趋于稳定，但在丝杆转速反向这一过程中，丝杆转速幅值有所变化，随后丝杆转速变化趋于稳定。