基于动力学的搬运机器人运动规划控制算法与仿真

满文镖，李艳杰，卜春光，高英丽，郎智明，眭晋

（1.沈阳理工大学机械工程学院，沈阳 110016; 2.中国科学院沈阳自动化研究所，沈阳 110016）

0 引言

面向危楼伤员救援需要，基于移动操作协调技术路线，我团队研制出伤员搬运机器人和运载机器人。搬运机器人负责将伤员从地面抬起并在合适的位置、高度移交给运载机器人，搬运机器人本体由2自由度履带式移动机构、5自由度机械臂和伤员搬运工具构成，机器人运动自由度数总计为7个，运动自由度存在冗余。机器人搬运对象为伤员，为了提高搬运过程伤员的安全性、舒适性，如何规划机器人搬运运动，确定自由度冗余情况下搬运机器人运动学逆解，控制机器人保持伤员、机器人重心稳定，避免倾翻危险，是搬运机器人需要解决的关键核心问题。

关于冗余自由度机器人不同需求运动规划的应用，通过动力学模型的建立，文献[1]、[2]分别提出时间最优和能耗最优的轨迹规划方法；为实现实时轨迹规划，文献[3]基于雅可比矩阵提出了人工势场轨迹规划方法，文献[4]利用虚拟排斥速度场和机械臂自运动特性实现了避障的运动规划；文献[5]考虑避障环境为封闭类管道下进行零件喷涂，提出基于碰撞反馈的冗余机械臂避障算法；文献[6]通过改进麻雀搜索法对超冗余机械臂进行轨迹规划；针对双足多自由度机器人，文献[7]实现18自由度双足机器人的全身运动规划，文献[8]、[9]考虑倾斜地面，针对多自由度双足机器人行走的最优轨迹进行运动规划。

针对倾翻问题，文献[10]针对两足机器人的运动稳定性进行分析，文献[11]针对两足机器人接触点的平衡稳定性进行研究，文献[12]针对两足类人生物在不平坦和倾斜地面的动态稳定行走控制进行研究；文献[13]针对履带式移动机器人越障问题，使用质心投影法和ZMP对静态稳定性和动态稳定性分析，得出其越障范围。

通过国内外现状分析，具有自由度冗余的机器人运动规划方法，主要采用优化思想；针对考虑安全、防止倾翻的机器人运动控制，主要通过对机器人动力学稳定性进行优化来实现。本文研究的搬运机器人，机构自由度冗余，搬运对象为伤员，需要避免倾翻、确保稳定安全，因此，现提出一种在保证安全性、稳定性的前提下搬运机器人搬运伤员的运动规划方法，使得伤员的安全得到保证，有效地提高机器人的救援效率。

1 算法思路

本文采用基于动力学稳定性优化实现搬运伤员运动规划和控制的方法。该方法重点保证3个目标：1）搬运过程保持机械臂末端承载伤员的搬运工具运动稳定；2）搬运过程保持机器人关节空间运动平滑稳定；3）保证机器人重心稳定，避免倾翻。思路如图1所示。

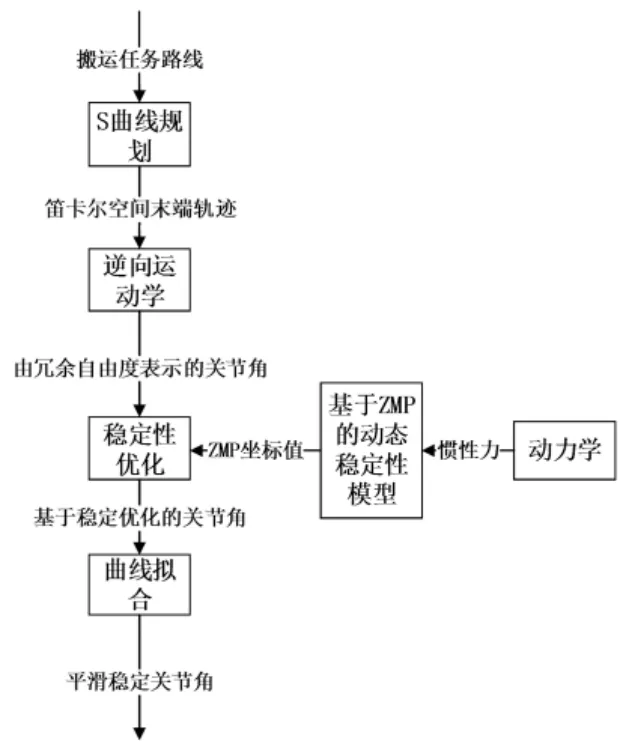
图1 算法思路

2 搬运机器人运动学建模

运动学建模包括正运动学和逆运动学两部分，本文重点在于逆运动学，正运动学是为了进行逆运动学的准备。

2.1 搬运机器人正向运动学

机器人三维模型及坐标系定义如图2所示。

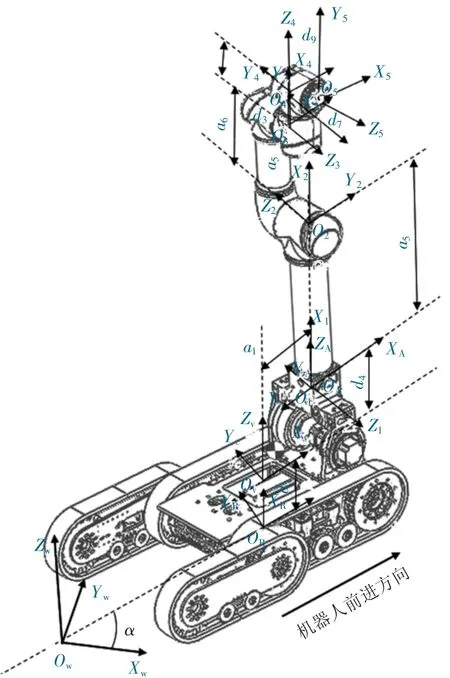
图2 搬运机器人坐标系

图2中：OW为世界坐标系；OR为机器人坐标系；OV为车体坐标系；OA为机械臂坐标系；O1、O2、O3、O4、O5分别为机械臂关节一、二、三、四、五坐标系。

本文采用改进DH法进行搬运机器人运动学建模。基于坐标系定义，改进D-H参数确定如表1所示。

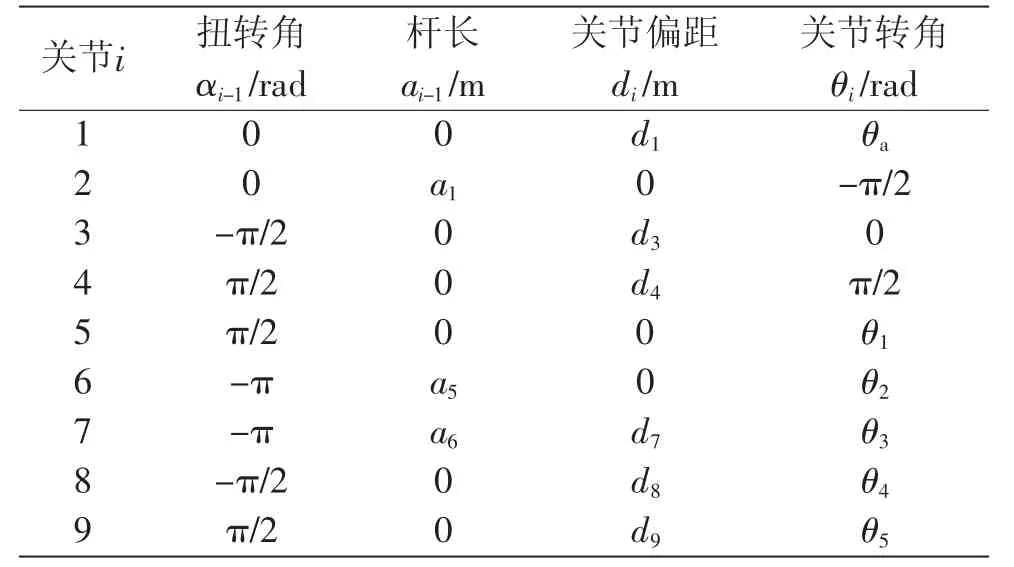
表1 机器人连杆改进D-H参数表

其中，关节1和3对应车体旋转和移动，关节5～关节9对应五自由度机械臂。为满足MATLAB建模需要，引入虚拟关节2和关节4。

根据改进D-H表，末端坐标在世界坐标系中的矩阵迹表达式为

正向运动学通过MATLAB 仿真试验得到验证。仿真试验模型及验证试验关节角和机械臂末端笛卡尔坐标如图3所示。

图3 MATLAB机器人正向运动学仿真验证截图

2.2 搬运机器人逆向运动学

假设：机械臂末端坐标系在世界坐标系下的表示为

得

解得：

求得关节八的角度为

求得关节九的角度为

令：

求得关节六的角度为

令：

求得关节五的角度为

根据式（10）得出关节七的角度为

根据作业过程机械臂时间最短筛选确定关节角唯一解。

结合正向运动学，利用双向计算方法基于MATLAB验证了逆向运动学的有效性。

3 搬运机器人稳定性建模

搬运机器人整体稳定性分析包括两部分：一是动力学建模；二是动态稳定性建模。

3.1 动力学建模

考虑搬运机器人移动操作机构复杂性，本文采用拉格朗日法推导搬运机器人动力学方程。

3.1.1 求动能K

为求解机器人的动能K，需要确定连杆的线速度和角速度，为此，需要确定雅可比矩阵，具体包括线速度雅可比矩阵和角速度雅可比矩阵。

为获得线速度雅可比矩阵，计算各连杆i的质心在世界坐标系下的表达为

进而线速度雅可比矩阵计算公式为

连杆质心线速度为

对于角速度雅可比矩阵计算，旋转关节用旋转轴向量表示，移动关节用0向量表示，故搬运机器人角速度的雅可比矩阵为

则连杆质心角速度为

基于上述公式推导可得动能方程为

机器人的质量矩阵为

3.1.2 求势能U

根据式（18），求得搬运机器人单个关节的势能：

根据式（25），求得搬运机器人的整体的势能为

3.1.3 求动力学方程

将动能和势能代入拉格朗日函数为

最后得到机器人系统的动力学模型为

3.1.4 正逆动力学

对于式（28），通过正动力学求解，已知各关节驱动力矩τ、连杆质心规划姿态θ、连杆质心规划速度θ˙，求解各连杆质心的惯性力（即加速度），进行稳定性分析。

3.2 搬运机器人稳定性分析

本文结合动力学分析机器人整体动态稳定性。动态稳定性指机器人移动操作过程系统平衡特性，与机器人运动学模型和动力学模型有关，本文采用零力矩点（ZMP）方法进行动态稳定性分析。ZMP指某一时刻机器人在支撑面上所有主动力矩之和为0的点，对于整体系统该点只有垂直方向的地面反作用力。搬运机器人保持平衡的一个必要条件是运动过程中ZMP始终落在稳定区域内[14]。

通过动力学计算关节转矩和连杆运动关系，根据式（28）可得各部位惯性力为

本文研究运动规划问题，不考虑不可预知的外力和外力矩作用；考虑伤员搬运安全性，速度不能过高，为此ZMP简化为

式中：g为重力加速度，xi、zi为连杆i质心z、x方向坐标，为连杆i质心沿参考坐标系z、x方向的加速度。

为满足系统稳定性，ZMP点必须在稳定区域之内，因此稳定性的判定依据为

式中：Xmin为机器人稳定区域的极限最小值，Xmax为机器人稳定区域的极限最大值。

4 S形轨迹规划

针对机械臂末端点对点的运动规划，将伤员从地面移交给运载机器人。常用的速度规划方法有S形轨迹规划、梯形轨迹规划，对于伤员搬运过程，其主要需求在于速度、加速度的连续，与梯型轨迹规划方法相比，S形轨迹规划时间会增大，但运动更加平稳，可保证速度、加速度的连续性，实现末端伤员的安全移动。

为进行S形轨迹规划，计算其末端最大速度、最大加速度。根据雅可比矩阵，建立关节额定速度q˙和末端速度的关系为：

根据能量守恒，能量不因坐标系不同而改变，结合式（32）可以得到末端加速度a和关节额定力矩τ之间的关系为

通常S形轨迹规划分为7段，分别是加加速段、匀加速段、加减速段、匀速段、减减速段、匀减速段、减加速段，每段都有对应的运动学参数，vti、ati、sti对应i段对应的速度、加速度、位移，加加速度为j。

在加加速段有：

在匀加速段有：

在加减速段有：

在匀速段有：

在减加速段有：

在匀减速段有：

在减减速段有：

总距离计算公式为

对于S形曲线，按照是否有匀速段、匀变速段可以分为3种情况，上述公式是有匀速段和有匀变速段，另外两种情况下，计算时需要保证加速度连续。

5 基于稳定性优化的冗余自由度机器人逆运动学解确定

S形轨迹规划得到机器人末端运动轨迹，这里利用稳定性优化确定冗余变量机器人移动自由度，进而求解其他关节变量。

计算机器人的动态稳定性，根据式（18）、式（29）得到连杆质心坐标xi、zi，以及连杆所受惯性力。

最后，将机器人各部位质心坐标和惯性力代入式（30），得到零力矩点在惯性坐标系的表达式，计算ZMP的坐标值。

对于搬运机器人，支撑面是指车体与地面接触点构成的接触面积。根据ZMP的坐标值与稳定裕度的关系可以得到最优稳定性判据为：

搬运机器人稳定性优化解析法模型为非线性高耦合方程，为此本文使用数值解法，计算搬运机器人的最优稳定性。

图4表示稳定性最优时机械臂关节一的角度变化过程。由图4 可以看出，机器人关节运动出现明显不平滑，突变剧烈。

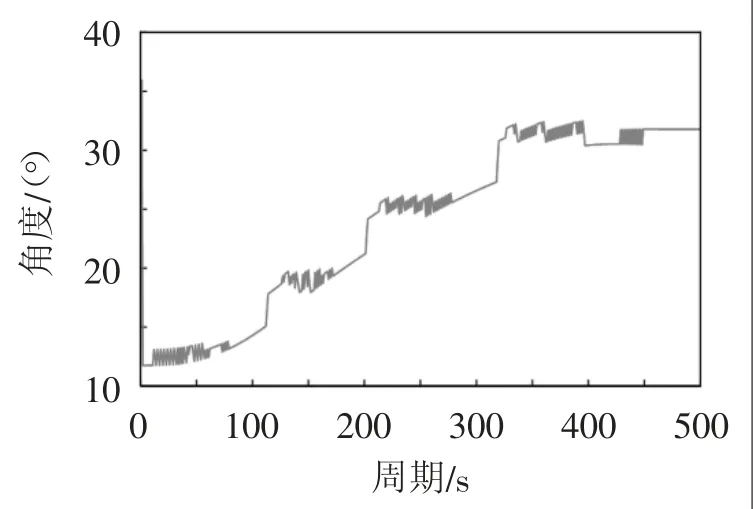
图4 机械臂关节一的角度

对于搬运任务，关节出现加速度突变会导致震颤，会导致伤员脱离搬运装置，或者二次受伤，使伤员安全受到威胁。而且，对于电动机来说，持续的加速度突变会导致关节的使用寿命大幅度缩减，并且会在执行救援任务时，因为机械臂本身能力不足以支持长时间工作而发生失控现象。为了避免出现这种现象，需要对于关节运动进行平滑处理。

本文采用零相位滤波中的巴特沃斯滤波对稳定性优化结果进行平滑处理。

首先针对稳定性优化的车体移动动态轨迹进行拟合平滑处理，然后利用冗余自由度逆运动学确定其他关节运动轨迹。

6 仿真验证

本文针对搬运机器人将伤员搬运移交到运载机器人担架上的过程，设计末端点的位置坐标，结合目标伤员搬运机器人在SolidWorks中的自身物理参数及关节数据，计算稳定性对应最优数值解，最后求解轨迹中关节角度的数值，并采用巴特沃斯滤波进行平滑处理；利用MATLAB仿真，通过稳定性的范围和运动加速度的平滑性验证算法有效性。仿真中图像的周期与时间的转化为T=0.2465 s。

6.1 仿真输入数据（如表2～表6）

表2 路线对应的始末点坐标值m

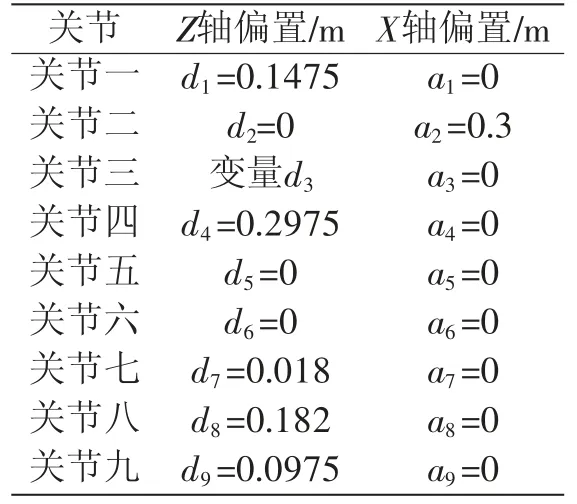
表3 运动学参数

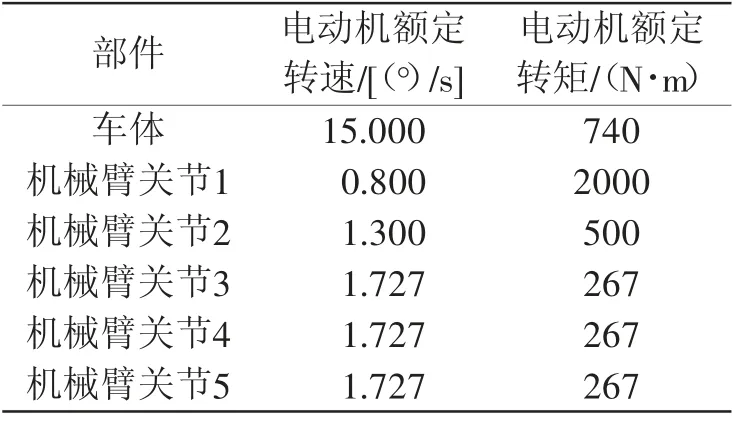
表4 关节参数

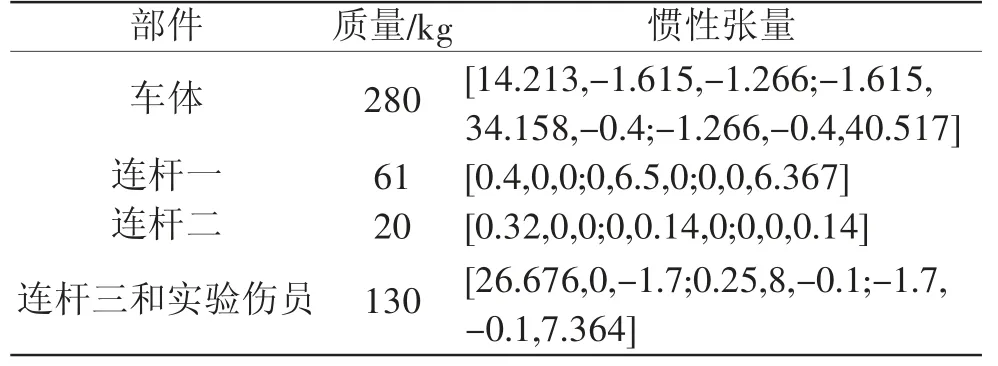
表5 质量参数表

表6 Z MP稳定区域坐标值m

表7 巴特沃斯滤波参数表

6.2 仿真结果

1）S形轨迹规划仿真。机器人末端沿着世界坐标系z轴方向轨迹规划的位移、速度、加速度如图5～图7所示。从图5中可以看出，在z方向上末端按照表2的起始点运动到终点；图6中速度和图7中的速度、加速度曲线连续，无突变点，符合S形轨迹规划，满足末端安全需求。

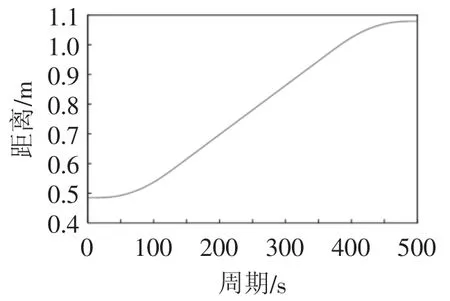
图5 末端Z方向移动

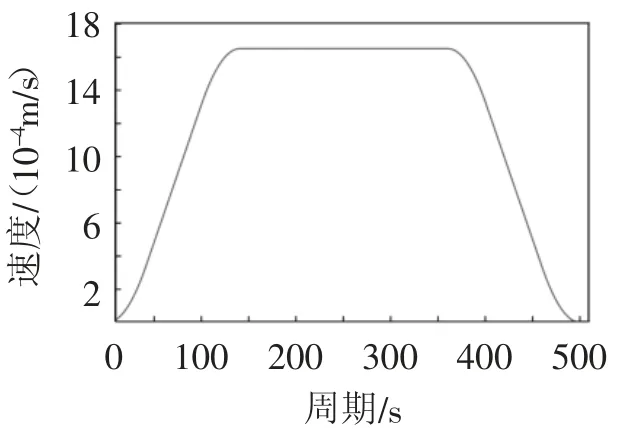
图6 末端Z方向移动速度

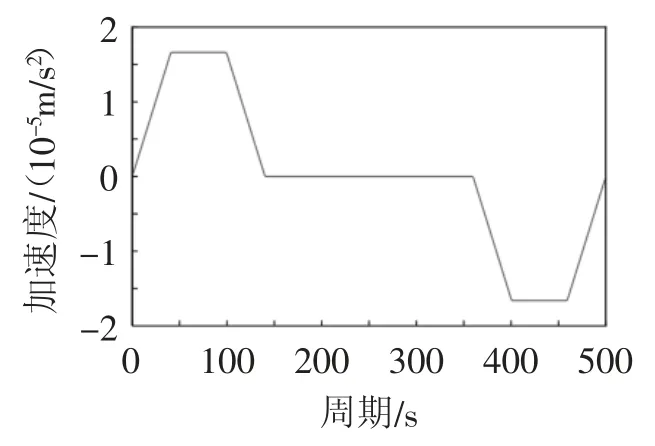
图7 末端Z方向移动加速度

2）稳定性仿真。机器人整个运动过程中的xzmp如图8所示，表示机器人自身的稳定性，运动过程中，xzmp的数值为-0.4～0.1 m ，由表6得知，其x方向稳定区域的范围为-0.7～0.5 m，xzmp的数值在稳定区域内。

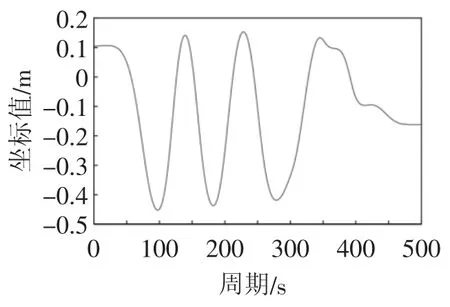
图8 xzmp

3）关节变化图像。根据冗余自由度逆解得到的平滑拟合后的6个关节角度、角速度、角加速度，如图9～图20所示，因为末端需要保持人体姿态不变及移动作业要求，过程中车体旋转和机械臂关节四、关节五角度处于相对静止。

图9 车体移动距离

图10 车体移动速度

通过对图4和图12进行比较，平滑拟合后的关节角度、速度平滑，减少了关节角度的频繁突变。通过图9～图20说明平滑拟合后的所有关节满足机器人关节连续运动的要求。

图12 机械臂一关节角度

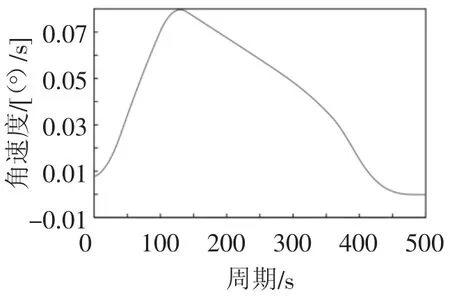
图13 机械臂一关节角速度

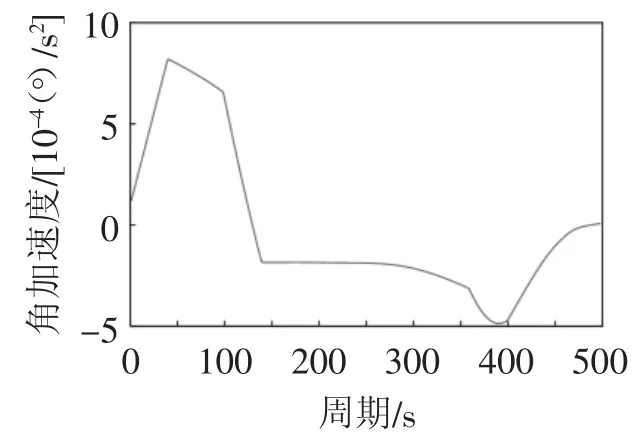
图14 机械臂一关节角加速度

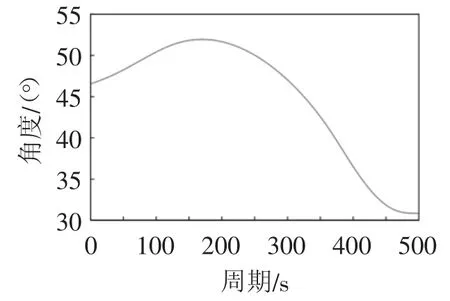
图15 机械臂二关节角度

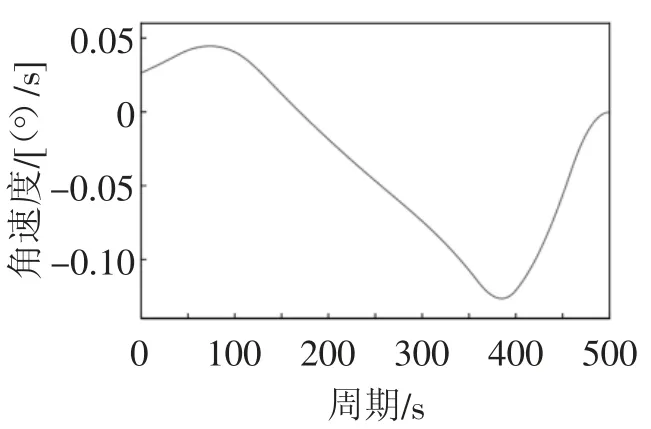
图16 机械臂二关节角速度

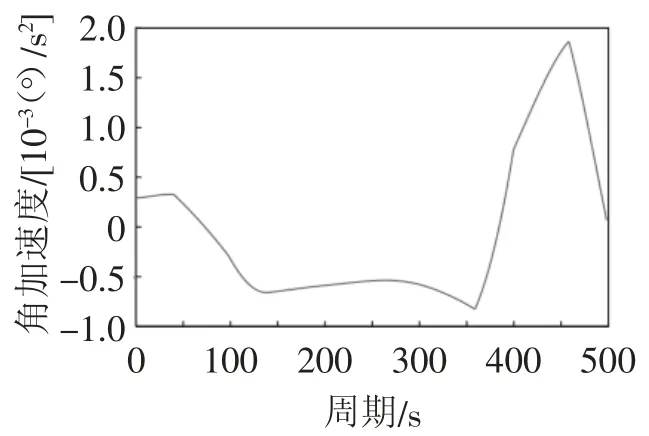
图17 机械臂二关节角加速度

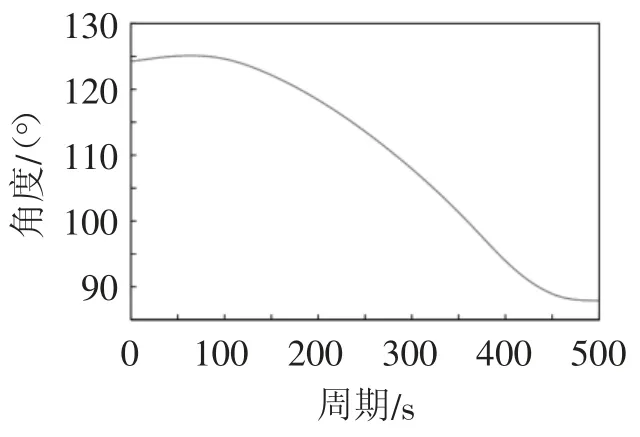
图18 机械臂三关节角度

图19 机械臂三关节角速度

图20 机械臂三关节角加速度

7 结论

本文针对自由度冗余搬运机器人搬运伤员过程稳定性要求，提出对于基于动力学稳定性分析的机器人轨迹规划和控制方法，并进行了仿真验证，主要结论如下：1）针对自由度冗余搬运机器人，推导出机器人运动学和动力学方程；2）结合S形轨迹规划、动态稳定性、求解最优解、关节角平滑处理，实现了伤员、机器人、关节稳定的机器人运动规划和控制；3）仿真结果表明，针对搬运机器人，该算法可以完成搬运任务，并能满足实际任务安全性、稳定性的需求。