基于响应面法的刚性太阳翼可靠性分析

文洋，咸奎成，倪啸枫，吕箴，智鹏鹏

（1.电子科技大学机械与电气工程学院,成都 611731; 2.上海宇航系统工程研究所, 上海 201109）

0 引言

随着航天器的不断更新换代，其功能和性能要求不断提高，进而对空间大型柔性结构的可靠性要求也随之增加。刚性太阳翼作为典型的空间大型柔性结构，其可靠性对卫星系统安全运行至关重要。然而，刚性太阳翼在工作过程中经常受到不确定性因素影响，如几何尺寸、材料特性和载荷条件等，加之载荷和材料性能的动态变化，使其可靠性变化不均且具有动态性。为此，在考虑不确定性服役环境的条件下，对刚性太阳翼进行可靠性分析具有重要的意义。

目前，众多学者开展了针对空间大型柔性结构的可靠性研究，陈建军等[1]针对大型展开天线结构的多阶段多状态性，提出了可靠性综合分析方法；杨翊等[2]对太阳翼驱动机构进行了系统可靠性建模和评估；在此基础上，李彦峰等[3]开展了更加完全的基于贝叶斯网络的系统可靠性评估方法研究；王晶燕等[4]对机械太阳翼的可靠性度量指标进行了分析与总结；刘帅杰等[5]在概率不确定性分析的基础上，进一步扩展了不确定性来源的描述，形成了对大型空间结构的认知不确定性分析方法。

上述研究多以数据为驱动，采用数值分析的方法进行空间大型柔性结构的可靠性分析，尽管能够得到较好的分析结果，但数据量过大，计算繁琐，不利于工程应用。为此，本文以刚性太阳翼为对象，提出了基于响应面法的可靠性分析流程，利用二次多项式函数量化根部铰链阻力距、板间铰链阻力距、钢丝绳刚度等不确定因素与帆板展开角度差的函数关系，依据等距曲线构成原理，确定了刚性太阳翼帆板角度差阈值区间范围，进而基于极限状态方程，实现了刚性太阳翼的可靠性分析。

1 刚性太阳翼结构组成及基本原理

刚性太阳翼是由多个太阳电池板组成的阵列结构，其作用为：将太阳能转换为电能，供卫星系统使用。当前广泛使用的太阳翼形式是刚性基板结构的折叠式太阳翼，主要由内板、中板、外板、连接架、根部铰链、板间铰链、连接架联动和板间联动等组成，其工作状态如图1所示。

图1 刚性太阳翼工作状态示意图

由图1可知，刚性太阳翼工作状态主要分为折叠和展开两种状态，当刚性太阳翼为卫星系统提供能源时，根部铰链和板间铰链扭簧的弹性势能转化为太阳翼各块电池板运动的动能，太阳翼各块电池板在根部铰链和板间铰链扭簧力矩驱动下依次展开；当卫星系统变轨或暂停工作时，刚性太阳翼解除锁定机构，收拢折叠。

2 刚性太阳翼可靠性分析方法

2.1 基于响应面的性能函数表示

刚性太阳翼作为典型的运动机构，其可靠性主要由运动精度度量。而不确定性载荷及其材料属性作为影响运动形变的主要因素，对其可靠性具有重要影响。鉴于刚性太阳翼结构复杂，其性能函数难以用常规物理方程描述，因此采用二次多项式响应面模型表征其输入-输出的函数关系[6-7]，其基本表达式为

式中：x为不确定性变量向量矩阵；xi（i=1,…,n）为随机变量；ai、bi、c为待定参数，共有2n+1个。

由第1节可知，刚性太阳翼帆板在太阳电池板的压力、阻力矩及自身参数等因素的影响下，展开过程会产生偏移，当偏移量超出阈值时，导致展开状态不满足规定要求。因此，将帆板展开角度差作为评判其可靠性的指标有助于合理评判刚性太阳翼的工作状态。

然而，根部铰链阻力距、板间铰链阻力距及钢丝绳刚度作为影响刚性太阳翼帆板展开角度差的主要因素，直接影响其可靠性。因此，刚性太阳翼帆板展开角度差的表达式可描述为

式中：M为根部铰链阻力距，T为板间铰链阻力距，E为钢丝绳刚度，f（·）为不带交叉项的二次多项式响应面函数。

考虑展开角度差随展开过程变化，式（2）可进一步描述为

联立式（1）和式（3），得到刚性太阳翼在t0时刻的性能函数表达式为

2.2 刚性太阳翼可靠性建模

刚性太阳翼工作过程中，要求帆板展开角度差不超过设计阈值，其极限状态方程可表示为[8]

式中：εd为设计阈值；εf为帆板展开角度差；当Z（x）＞0时，刚性太阳翼展开处于可靠状态；当Z（x）＜0时，刚性太阳翼展开处于失效状态；当Z（x）=0时，刚性太阳翼展开处于极限状态。基于式（5），刚性太阳翼在t0时刻的可靠度可表示为

综合上述分析，得到基于响应面法的刚性太阳翼可靠性分析流程，如图2所示。

图2 刚性太阳翼可靠性分析流程图

3 刚性太阳翼可靠性分析

3.1 刚性太阳翼展开过程仿真分析

由式（3）可知，影响刚性太阳翼可靠度的随机变量主要是根部铰链阻力矩、板间铰链阻力矩、钢丝绳刚度及时间。为保证仿真结果的准确性，选用完全析因方法进行试验设计，随机变量数字特征如表1所示，试验设计过程如表2所示。

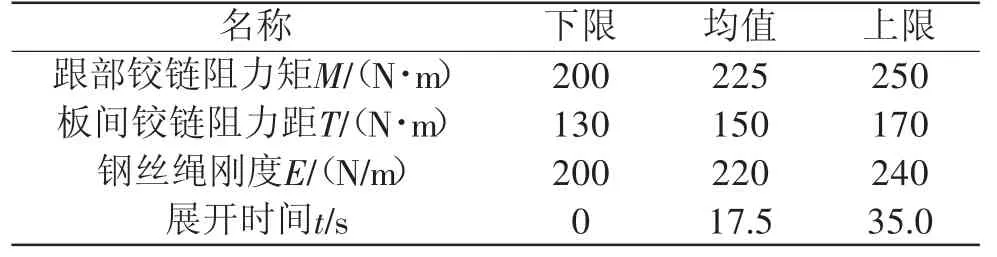
表1 随机变量数字特征

表2 试验设计及响应值

根据表1和刚性太阳翼的基本结构，建立其仿真分析模型，如图3所示。

图3 太阳翼帆板仿真模型

基于仿真分析模型，计算刚性太阳翼在27种不同工况下的帆板展开角度差，计算过程如表2所示。

为直观表达27种工况下帆板展开角度差随时间的变化规律，对表2中的数据进行绘制，得到帆板展开角度差随时间的变化曲线，如图4所示。

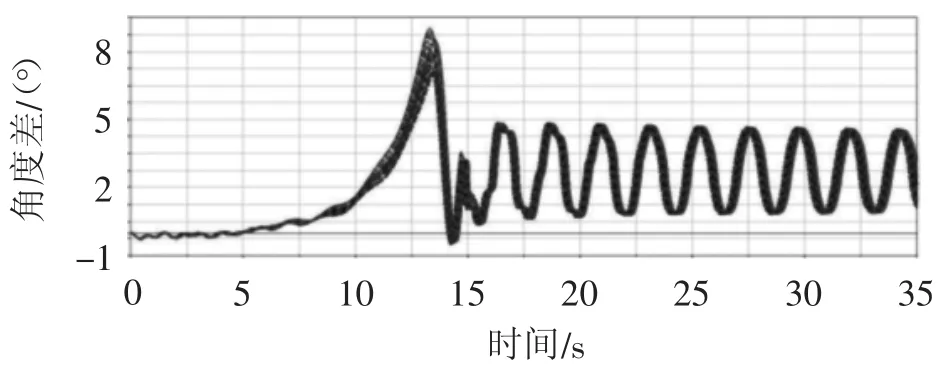
图4 帆板展开角度差随时间的变化曲线图

由图4可知，在35 s展开时间内，不同工况下帆板展开角度差变化趋势基本一致，均受不同时刻随机变量波动的影响。在0～15.5 s时，刚性太阳翼处于初始展开阶段，帆板展开角度差波动较大且无规律；在15.5～35 s时，刚性太阳翼处于稳定展开阶段，帆板展开角度差波动降低且趋于平稳，并呈现周期变化规律。

3.2 刚性太阳翼帆板角度差阈值区间确定

为获取刚性太阳翼帆板角度差阈值区间，根据图4仿真分析得到的不同工况下帆板角度差数据，计算27组仿真结果在每个时刻的均值，结果如图5所示。

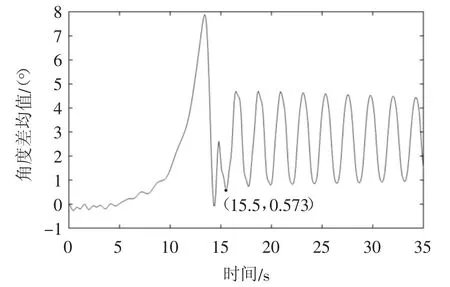
图5 帆板角度差均值曲线图

为精确对图5中的曲线进行函数表征，依据其变化规律将其分为［0,15.5］和（15.5,35］两个阶段进行拟合。

当t∈[0,15.5]时，其函数表达式为

当t∈（15.5,35]时，其函数表达式为

对式（7）和式（8）进行函数绘制，并与图5进行对比，结果如图6所示。由图6可知，分段函数拟合曲线与均值重合度较好，说明式（7）和式（8）的拟合精度较高，可用于后续计算。

图6 帆板角度差均值拟合曲线图

由文献[9]可知，当设计阈值为0.5时，刚性太阳翼的帆板角度差满足工作要求。依据等距曲线的构成原理，可确定刚性太阳翼帆板角度差阈值区间，如图7所示。

图7 帆板角度差上下限曲线图

由图7可知，当仿真分析求解的帆板角度差值超出阈值区间时，刚性太阳翼展开处于不可靠状态；反之，则是安全状态。

利用图8确定的帆板角度差阈值，对图4中的数据进行度量，其对比结果如图8所示。

图8 帆板角度差与设计阈值的对比曲线图

由图8可知，在t∈[0,35] s时，部分时刻出现帆板角度差超出阈值的情况，此时刚性太阳翼的服役状态存在不可靠风险。因此，需进一步对其进行可靠性分析，以确保其安全运行。

3.3 刚性太阳翼可靠度计算

根据图8中的对比结果，联立式（4）～式（6），得到t∈[0,35] s时的刚性太阳翼可靠度，如图9所示。

图9 可靠度变化曲线图

由图9可知，t∈[0,35] s时，刚性太阳翼服役性能整体处于可靠状态；t∈[12,16]时，可靠度下降，其趋势与图8中超出阈值部分保持一致。

以0.05 s为时间间隔，对可靠度下降区域进行精确分析，结果如图10所示。由图10可知，刚性太阳翼展开过程中的可靠度在13.4 s和14.8 s时到达极小值点，此时可靠度较低，分别为0.777 12和0.499 72，表明该时刻的可靠性不满足要求，需进一步进行优化设计以保障刚性太阳翼可靠工作。

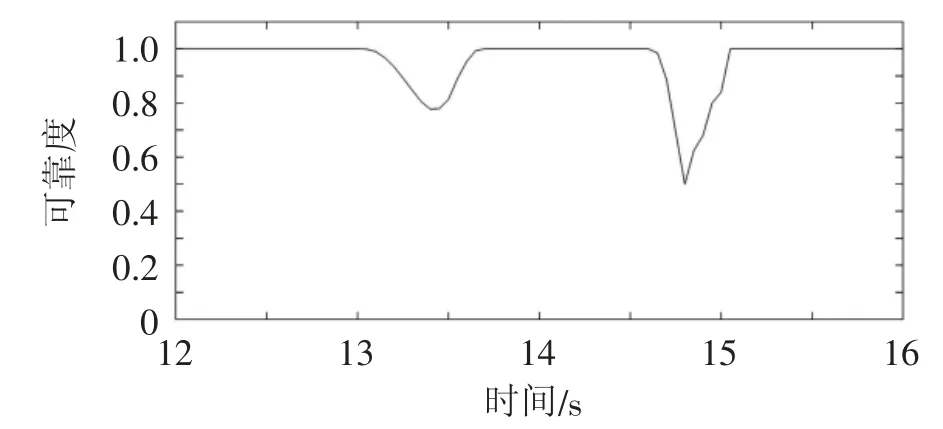
图10 可靠度局部变化曲线图

4 结论

本文以刚性太阳翼为研究对象，对其运动过程进行了仿真分析，确定了帆板角度差度量指标及其阈值区间，开展了基于响应面法的可靠性分析，得到以下结论：

1）依据刚性太阳翼工作原理，建立了基于响应面法的可靠性分析流程，解决了因刚性太阳翼结构性能函数缺乏导致其可靠性分析难的问题。

2）对刚性太阳翼结构进行仿真分析，明确了不同工况下帆板角度差随时间的变化规律，并确定了帆板角度差的阈值区间，为其极限状态方程的建立奠定了基础。

3）通过对刚性太阳翼进行可靠性分析，得到了t∈[0,35] s时刚性太阳翼可靠度的变化情况。结果表明：t∈[12,16]时，可靠度下降；在13.4 s和14.8 s时可靠度达到最低，分别为0.777 12和0.499 72，说明该刚性太阳翼在工作过程中存在可靠度不满足要求的情况，需对其进行进一步优化。