基于集成机器学习模型的短期光伏出力区间预测
2024-02-27陈习勋吴凯彤彭显刚
陈习勋,吴凯彤,何 杰,彭显刚
(1.广东电网有限责任公司汕头供电局,广东汕头 515041;2.广东工业大学自动化学院,广东广州 510006)
0 引言
光伏发电在世界范围内得到普遍的开发应用,对改善全球气候变暖以及缓解全球能源危机发挥着积极的作用[1-2]。但是,光伏发电功率容易受到所在区域范围内的多种气象因素如太阳辐照度、温度及相对湿度等直接或间接的影响,导致光伏出力具有一定的随机性、间歇性和不确定性等特点。分布式光伏的大规模并网会对电力系统运行的稳定性和可靠性造成不利影响[3]。可见,提高短期光伏出力的预测精度显得十分迫切。传统的点预测方法无法精准量化不确定性大小,不能适应电力系统安全风险精准评估的应用需求,而光伏出力的区间预测不仅能够有效量化光伏出力的不确定性,还能定量描述光伏出力的概率区间,为电网调度人员提供更为全面的预测信息[4]。
目前,常用的点预测方法主要有时间序列模型[5-6]、深度学习模型[7-9]以及混合模型[10-12],这些方法利用历史光伏数据以及气象数据来确定某时刻光伏出力值,具有一定的局限性,无法准确描述光伏出力的不确定性。为了更直观地量化光伏的不确定性以及准确捕捉光伏出力的时序信息,许多学者将研究重点转移到光伏的出力区间预测上。文献[13]提出了一种基于高斯混合模型的光伏概率区间预测方法,虽然该方法的预测结果优于典型单一分布模型,但该方法并未与点预测方法进行对比分析。文献[14]利用藤Copula 对光伏功率及其相关变量间的关联结构进行解析,建立条件分位数回归模型预测光伏功率的概率密度函数。文献[15-17]都提出基于深度学习的混合模型模型,并将其应用于光伏功率预测,这些方法的预测效果不错,但无法准确描述光伏出力的随机性和波动性。文献[18]提出一种基于高阶马尔可夫链和高斯混合模型的光伏电站短期出力概率预测方法。文献[19-20]中使用到的预测模型具有相同的预测模式,都利用气象数据和历史光伏出力数据进行短期光伏预测,都是利用历史光伏数据以及气象数据来确定某时刻光伏出力值,具有一定的局限性,无法有效地量化光伏出力的不确定性。文献[21]通过Copula 模型得到光伏出力的概率分布,但Copula 模型会因不同的函数形式而产生的不同的效果,实际工程中在选取Copula 函数形式上仍有难度。
本文提出一种基于快速相关性过滤算法结合集成机器学习模型(Fast Correlation-based Filter-Ensemble Learning,FCBF-EL)的短期光伏出力区间预测方法。针对输入特征冗余导致的预测误差,本文利用快速相关性过滤(Fast Correlation-based Filter,FCBF)算法提取日光伏出力预测模型的最优输入特征集;然后,将最优特征集输入到集成机器学习(Ensemble Learning,EL)预测模型中进行训练与测试;最后,基于EL 学习模型的预测结果,计算这组模型的预测概率密度函数,确定预测区间的上下限。本文选取澳大利亚爱丽丝泉一座光伏发电站数据进行仿真验证了所提模型的性能。
1 快速相关性过滤的特征选择算法
1.1 FCBF算法原理
FCBF 算法是一种采用后向顺序搜索策略快速有效寻找最优特征子集的特征选择方法,常采用对称不确定度(Symmetrical Uncertainty,SU)作为测量指标去衡量一个特征与目标变量是呈相关性还是冗余性。
假设离散随机变量X=[x1,x2,...,xm]和随机变量Y=[y1,y2,...,yn]。
式中:H(X)为变量X的信息熵,表达了取值的不确定性;H(X|Y)为变量X关于变量Y的条件熵,即在变量Y已知的前提下变量X的不确定性程度;I(X;Y)为表示在观察到Y随机变量后X变量信息熵减小的互信息,描述了2 个变量之间相互关联程度的大小;P(xi) 和P(yj) 分别为随机变量X=xi,Y=yj的概率;P(xi|yj)为随机变量Y=yj条件下随机变量X=xi的条件概率;m、n分别为随机变量X、Y所有可能取值的总数。
由于I(X;Y)的大小会受到变量值和变量单位的影响,需要对互信息进行了归一化处理,通常使用SU(X,Y)来计算2个随机变量之间的相关性大小,即对称不确定性的值,可用SU(·)来简化表示[22]。
由式(4)可知,SU(X,Y)的值介于[0,1]之间,其值越大,表明随机变量X和随机变量Y之间的相关性就越大。当SU(X,Y)=0,表示这2 个随机变量不相关,当SU(X,Y)=1,表示这2个随机变量完全相关。
1.2 FCBF特征选择算法实现步骤
FCBF特征选择算法主要包括2个步骤:
1)去除不相关特征:计算每个特征与类别之间的相关性,挑选大于阈值的特征组成候选子集。
2)去除冗余特征:对各子集采用SU度量准则以及近似马尔科夫毯(Markov Blanket,MB)条件筛选出相关特征并剔除掉冗余特征。
本文实现的FCBF特征选择算法详细流程图如图1所示。
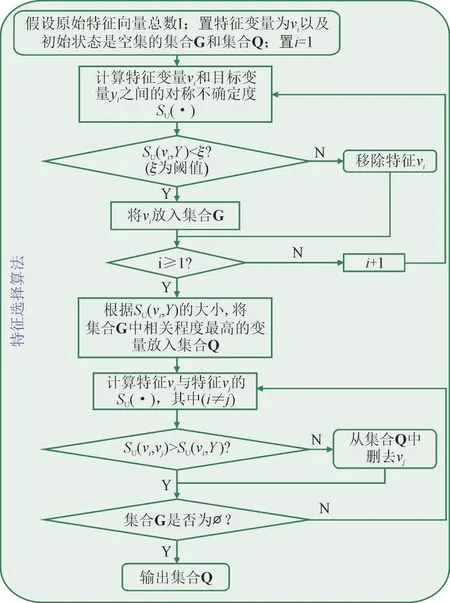
图1 FCBF特征选择算法的流程图Fig.1 Flow chart of FCBF algorithm
2 短期光伏出力区间预测模型
2.1 预测模型工作原理
本文通过集成决策树、支持向量机、K 近邻回归(KNN)、随机森林回归以及Bagging 回归等机器学习模型基学习器,可以构建集成学习模型(EL 模型)来实现整体预测精度的提升。本文提出的FCBFEL 模型工作原理总体结构框架如图2 所示。
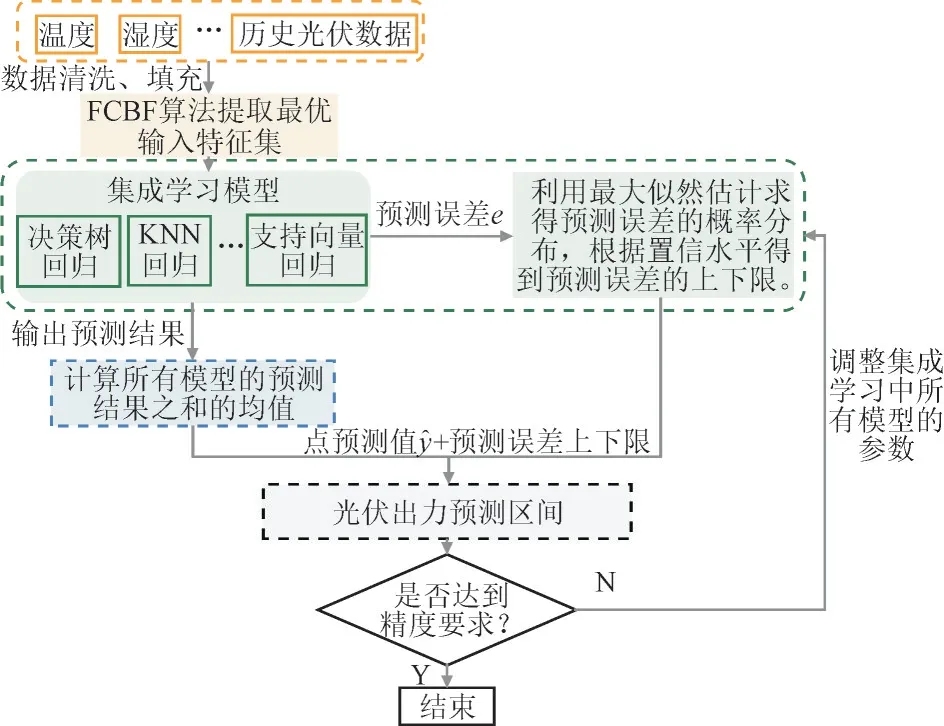
图2 集成机器学习模型的总体结构框架图Fig.2 Overall frame structure of integrated machine learning model
2.2 预测步骤
1)历史数据预处理。在收集数据的过程中,可能会出现数据缺失和数据异常的情况,在训练预测模型之前需要对原始数据进行清洗、填充以及异常值剔除等处理,然后对处理后的数据进行归一化处理。
2)最优特征集的提取及数据集划分。光伏出力对不确定性气象因素的依赖度高,原始数据集的采样间隔为5 min,其中包括温度、相对湿度、总水平辐射度、散射水平辐射度、风向以及日降雨量。
为了提高运算效率,减少预测误差,将原始数据以[x1,t,x2,t,…,xk,t,yt](k+1)×t的矩阵形式输入到快速过滤的特征选择算法中,根据FCBF 算法的工作原理筛选出最优输入特征集。其中,xk,t代表第k种特征在t时刻的数据,为列向量;yt代表目标光伏出力的列向量。基于多次实验证明,当特征向量与光伏出力相关度大于80%时,此时预测模型的预测效果最佳。
最优输入特征集被划分为训练集、验证集与测试集。其中,训练集占数据集的80%,用于训练模型;验证集占数据集10%,用于求解每个基学习器的最优参数;测试集占数据集的10%,用于评估该模型的预测性能。
3)构建并训练模型。单个基学习器往往只能在某些方面表现出色,而集成学习通过组合多个基学习器弥补这些基学习器表现不足的方面,构建1 个性能更全面、预测效果更好的强学习器。本文拟选用决策树、支持向量机、KNN 回归、随机森林回归以及Bagging 回归基学习器构建集成学习模型,每个基学习器的初始参数随机生成,将训练集以及验证集分别放入每个基学习器中进行参数调整,每个基学习器的损失函数是均方误差函数。为了减少初始化可调参数设置所造成的性能误差,本实验循环重复100 次集成学习的训练与验证过程,从中选取性能误差最优的一组参数作为模型参数。然后,收集每次循环得到的预测误差,通过最大似然估计,根据置信水平确定预测区间的上下限。
4)测试并评估。将测试集放入已完成训练的模型,对该组预测模型的所有预测结果求均值,并结合步骤3)得到的预测区间上下限,得到最终的光伏出力预测区间。判断预测结果是否满足精度要求,若满足跳转到步骤5),否则,跳转到步骤3),重新训练模型。
5)结束。输出预测日光伏出力的预测区间。
2.3 预测区间上下限的确定方法
假设随机样本满足某种概率分布,但又无法得知其具体的参数,最大似然估计就是1 种常用的参数估计方法。本文采用最大似然估计方法求得光伏出力预测区间的上下限,核心思想通过若干次试验,观察其结果,得知某个参数能使这个样本出现的概率最大,而其他参数使这个样本出现概率较小,因此可将这个参数作为估计的真实值[23]。
最大似然估计的步骤如下:
1)根据集成学习模型多次迭代得到的预测误差,写出预测误差的似然函数:
式中:ei为第i次迭代学习得到的预测误差向量;θ为所求参数向量,M为迭代学习次数。
2)对上述似然函数取对数lnL(θ)。
3)对参数θ1,θ2,…,θM求偏导数获得似然方程组:
4)求解式(6)。判断方程组是否有解,若有,则为所求的最大似然估计;否则,最大似然估计常在θj的边界点上得到。
5)根据对数似然方程组的解,确定目标似然函数中的参数估计值,得到预测误差变量的概率分布。
6)然后,将所有的预测误差分别与负荷预测曲线相加,相加的结果仍服从预测误差的概率分布。最后,根据所选取的置信水平,提取出满足要求的预测区间上下限。
2.4 评价指标
本文采用2 类不同的评价指标对所提模型的预测效果进行直观地评价。
第一类评价指标是常用于评价点预测效果的指标[24]:平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、均方根误差(Root Mean Square Error,RMSE)。MAPE,RMSE 的值分别用EMAP,ERMS表示:
第二类为常用于评价概率预测的指标:预测区间覆盖概率(Prediction Interval Coverage Probability,PICP)以及预测区间归一化平均宽度(Prediction Interval Normalized Average Width,PINAW)。PICP,PINAW 的值分别用PPIC,WPINA来表示。PPIC描述预测区间的可靠性,其值越大,说明越可靠;WPINA描述预测区间宽度的精准程度,一般其值越小越好[25]。
式中:Li和Ui分别为第i个预测区间的下界和上界;R为负荷实际值的范围(用于归一化)。
当yi∈[Li,Ui]时,ci=1,否则,ci=0。
3 算例分析
3.1 光伏出力数据集划分及预处理
本文使用的光伏出力数据是来自澳大利亚光伏研究中心(DKASC)的某1 个太阳能发电系统,该系统采用天合光能单晶硅阵列,大型双轴跟踪器,装机容量为23.4 kW[26]。原始数据集是该发电站在2019—2020 年的光伏出力数据,每5 min 采样1次,每1 天共288 个点。由于7:00 前以及19:00后无太阳辐射量,发电量几乎为0,因此,在实验过程中只采用7:00—19:00 间144 个采样点的光伏发电数据。实验计算机配置为:处理器Intel(R),Core(TM),i7-10510U,CPU 1.80 GHz 处理器,基于Python3.9运行环境。
在进行实验前,需要对原始数据进行归一化处理,标准归一化的公式为:
式中,x为原始光伏出力数据集;xmax和xmin分别为该数据集的最大值和最小值;xg为标准归一化后的数据。
从式(11)中可得出xg的取值会落在区间[0,1]中。
本文从原始数据集中提取2020 年1 月至2020年8 月的光伏出力数据作为算例分析,验证所提方法的预测性能。训练集与测试集的划分如下:训练数据占原始数据集的80%,验证集占训练数据的20%;原始数据集余下部分为测试数据。
3.2 最优特征集的选取
本文选择11 个特征量如表1 所示,包括温度、相对湿度、总水平辐照度、散射水平辐照度、风向、日降雨量以及预测日前5 日每天的光伏出力等。假设目标值为预测日的光伏出力,利用FCBF 特征选择算法,寻找最合适预测模型的输入特征集。基于FCBF 算法选择的特征向量相关性如表1 所示。本文将选取相关性大于80%的特征向量作为预测模型的最优特征输入集。
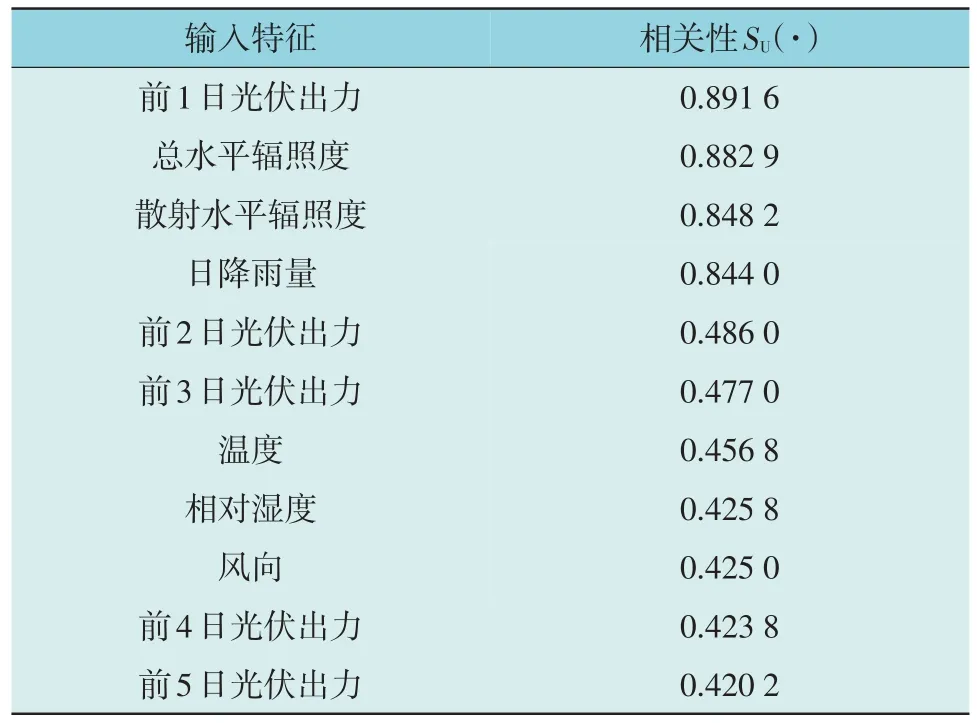
表1 特征向量与光伏出力的相关性Table 1 Correlation between feature vectors and photovoltaic output
其中,太阳的辐照度是影响光伏出力最直接的因素,而降雨可能会产生遮挡太阳对光伏板照射的光线的云层,间接导致光伏发电量大大缩减。因此,若预测日的降雨量较大,光伏的出力将大幅度下降,日降雨量对光伏出力会有较大的相关性。
3.3 实验结果分析
本文所提出的光伏出力区间预测方法是集成多个机器学习模型,结合不同基模型的优势获得准确的未来光伏出力区间。经过多次实验发现,当置信水平设置为90%时,所提及模型的预测性能最佳,为保持一致性,所有区间预测模型的置信水平均设置为90%。为了证明所提出方法的有效性,在相同的条件下,分别与Adaboost、支持向量回归(Support Vector Regression,SVR)、长短期记忆网络(Long Short-Term Memory,LSTM)、门控循环单元(Gated Recurrent Unit,GRU)、高斯过程回归模型(Gaussian Process Regression,GPR)、深度学习分位数回归模型(Deep Learning Quantile Regression,DLQR)进行对比实验。此外,为了验证FCBF 特征选择算法的优势,基于最小冗余最大相关特征选择算法的集成学习模型也参与对比实验中。
所提方法与GPR,DLQR 以及基于最小冗余最大相关特征选择算法的集成学习模型(Minimum Redundancy Maximum Relevance-Ensemble Learning,MRMR-EL)的预测区间对比如图3 所示,其中展示了7:00—19:00 之间的144 个时间点的曲线,其中红色实线为光伏出力真实值,蓝色实线为光伏出力预测值,绿色区域代表光伏出力在置信水平为90%下的预测区间。从图3 中可看出,本文所提方法得到的在置信水平为90%下的预测区间不仅能完全覆盖真实的光伏出力曲线,预测区间的归一化平均宽度比较窄,但是在光伏出力峰谷时区间宽度明显较宽,可能是光伏受不确定性因素影响较为突出导致的。
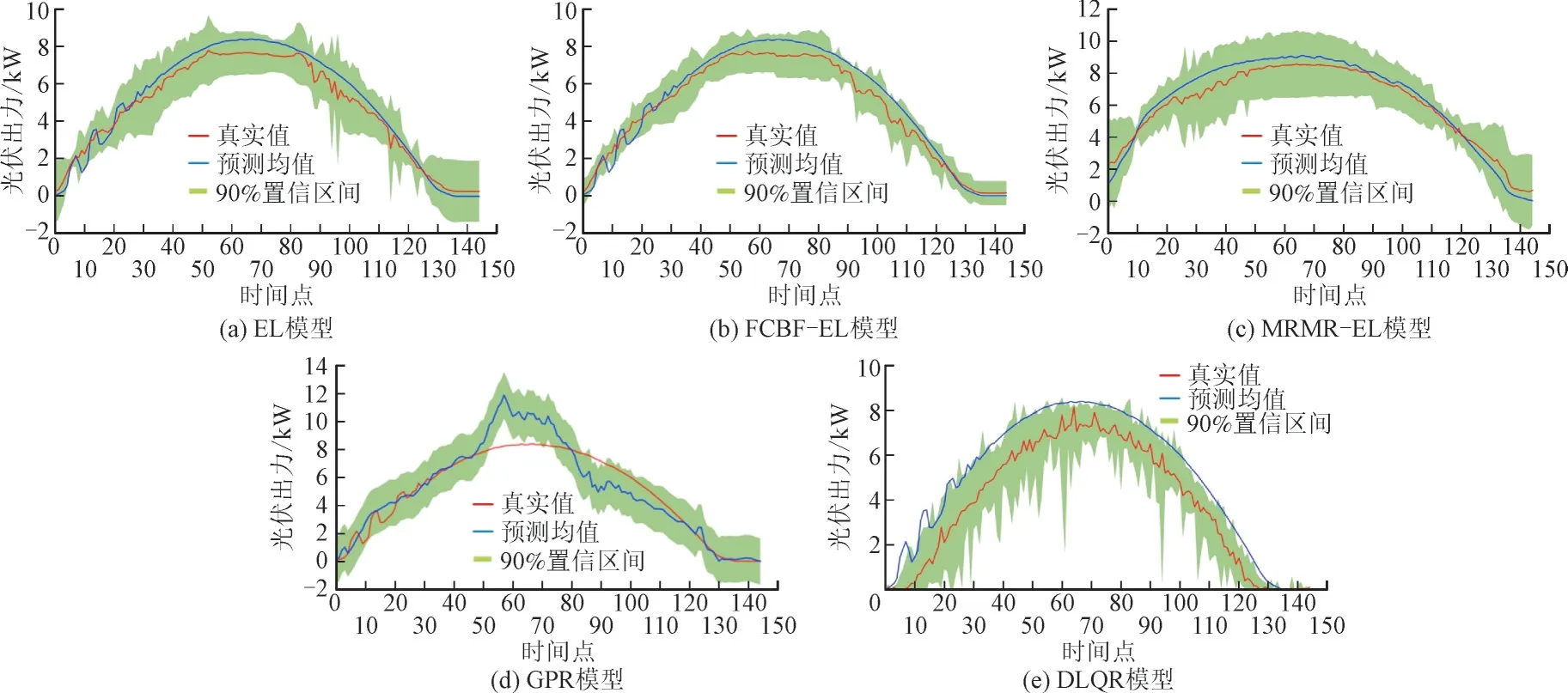
图3 集成学习模型与区间预测模型的预测结果Fig.3 Prediction results obtained by integrated learning model and interval prediction model
为了进一步证明本文所提方法的优势,本文列出了与其他几种不同模型的点预测方法的结果整体趋势对比如图4 所示。为了更直观地展示所提方法的优越性,图5 及表2 描述在不同评价指标下集成学习模型与其他预测模型的预测性能比较。
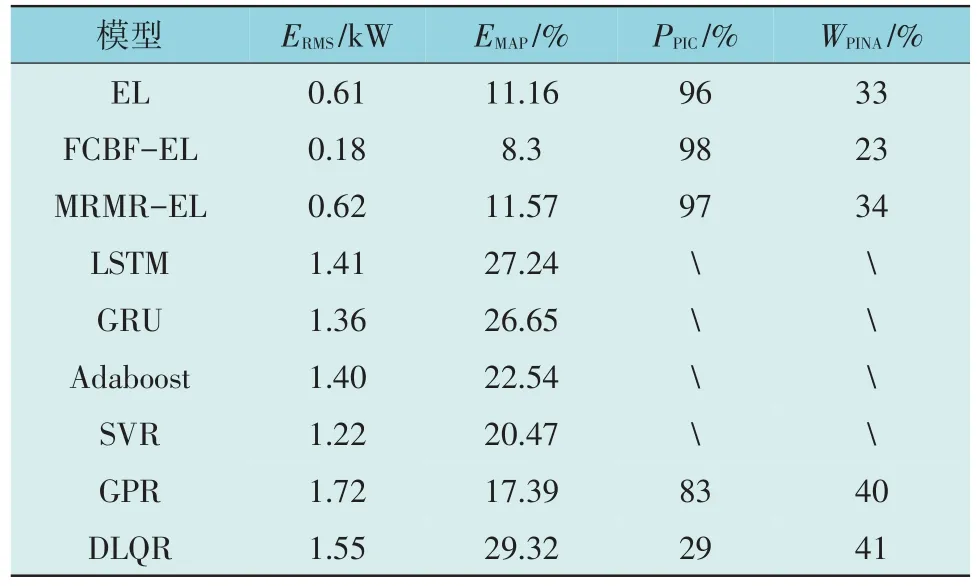
表2 各预测模型的评价指标对比Table 2 Comparison of evaluation indicators between prediction models
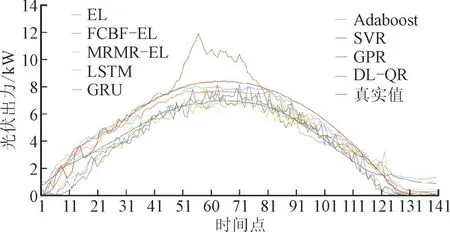
图4 集成学习模型与其他模型的点预测结果对比Fig.4 Comparison of photovoltaic output prediction results at different time points between integrated learning model and other models
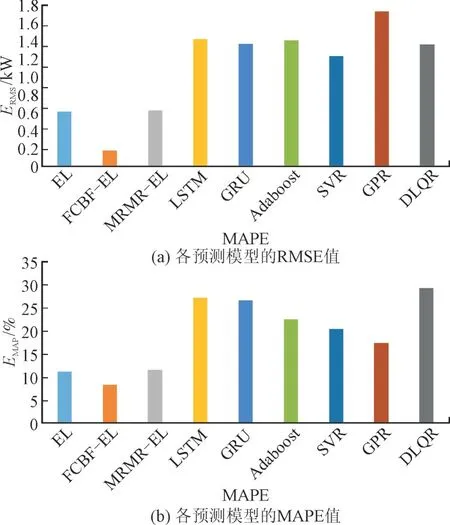
图5 各预测模型的评价指标Fig.5 Evaluation indicators of each prediction model
图4 给出了9 种不同的点预测模型预测结果对比曲线,在整体上所有曲线都能贴合光伏出力的变化趋势,而本文提出的FCBF-EL 方法的光伏出力预测值更接近真实值。其性能由图5 以及表2指标可明显看出,FCBF-EL 模型的RMSE 和MAPE是最低,是在所有模型中预测性能最为理想。而且相比于常用的区间预测模型,本文模型的预测区间覆盖率可达95%以上,证明所提出方法具有一定的优越性。
4 结论
本文构建了基于FCBE-EL 的短期光伏区间预测模型,而且还与常用的点预测与区间预测模型进行预测性能的比较。在同一条件下,通过实例分析并结合点预测评价指标以及区间评价指标进行不同模型的预测性能评估。研究结果表明:
1)集成学习模型能够融合基学习器的优点并弥补不同基学习器之间的不足,得到精度更高、稳定性更强的短期光伏出力预测结果。
2)快速相关性过滤特征选择算法能够降低冗余特征导致的预测误差,加入特征选择算法后能够进一步提高集成学习预测模型的光伏出力预测精度。
本文所提出的短期光伏出力预测模型在实际的工程应用中具有一定的前景和意义。但是本文基于集成机器学习预测模型仍存在不足,例如在集成学习模型中未加入优化参数的算法、在特征输入集中未考虑更近光伏站点的气象特征及未详细分析不同阈值下最优输入特征集对预测精度的作用,以上问题将成为日后工作的重点。
