预防双馈风机调频期间失速的功率轨迹预设策略

韩砚海，张浩松，杨德健，王 鑫，桑 顺

（1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林吉林 132012；2.南通大学电气工程学院，江苏南通 226019）

0 引言

随着化石能源日益消耗及“碳达峰、碳中和”战略目标的提出，风力发电、太阳能发电等新能源发电逐步取代以煤炭为能量来源的火力发电[1-2]。截至2021 年末，全国风电累计装机容量达3.28×108kW，预计2050 年将达到2.4×109kW[3]。

风电机组通过电力电子装置联网，与同步机组不同，风电机组中电力电子器件的应用使得风机转子转速与系统频率解耦[4-5]，对电网表现“零惯量”特性。大规模风电联网势必会导致系统整体惯性水平降低，恶化系统频率稳定性[6-7]。为提高系统频率稳定性，英国、丹麦、中国等国家均要求风电机组主动参与系统调频[8]。

系统发生扰动时，风机通过释放旋转动能弥补系统功率缺额，使其具有与同步机类似的惯量支撑特性，称为虚拟惯性控制[9-10]。虚拟惯性控制通常可以分为2 类：基于频率响应的虚拟惯性控制（Frequencybased Inertial Control，FBIC）和阶跃虚拟惯性控制（Stepwise Inertial Control，SIC）。

随着研究的深入，国内外学者提出了众多FBIC改进策略。文献[11]基于非互联孤岛系统的频率控制问题，讨论了风机参与一次频率控制和提供一次备用的能力。文献[12-13]针对传统FBIC 控制参数适应性差的问题，提出一种变系数模糊控制策略。文献[14]阐述了FBIC 响应延时的原因并定量分析了响应延时对调频效果的影响。FBIC 具有较好的调频效果且改进方法多样，但受频率测量滞后特性限制，其频率响应较慢。

相比于FBIC，SIC 无需时刻检测频率计算调频增发功率，具有更快的响应速度。文献[15-16]量化研究了商用多兆瓦变速风力发电机组提供短期过剩有功支持的能力，提出传统的SIC，以阶跃形预设功率轨迹响应频率扰动。但转速恢复阶段的大幅有功减载易引发严重的频率二次跌落。为此文献[17]根据系统频率实时滚动优化风机有功减载量，在抑制频率的二次跌落深度的同时兼顾转子转速恢复。文献[18]提出了风电机组调频功率评估方法，进而得到风电场的调频功率评估方法和风电场一次调频功率分配方法，有效避免转速恢复期间频率二次跌落。文献[19]在风机转速恢复阶段，借助一次递减函数在预设时间内将控制系数平滑减少至零，实现可控的转速恢复，同时消除转速恢复对频率的二次冲击。文献[20-21]分别以二次形、斜坡形功率下降轨迹代替传统SIC 阶跃形功率下降轨迹，有效减小频率二次跌落。但低风速场景存在风机失速隐患。文献[22]采用转矩极限设计双馈风机功率输出曲线，频率支撑阶段立即将转矩增大至极限值，可快速释放大量旋转动能提高频率最低点。但未考虑转矩极限带来的临界稳定问题，可能诱发风机失速。SIC 能够根据功率预设轨迹快速参与频率响应起到频率支撑作用，且功率轨迹灵活多变，能够根据调频需求灵活设计频率响应各阶段功率轨迹，达到不同的调频效果，但调频过程中存在旋转动能过度释放导致风机失速的隐患。

本文在斜坡形SIC 基础上，根据风机允许释放的最大旋转动能优化其部分参数，使功率线性下降阶段释放的旋转动能始终小于允许的最大值，防止了风机失速。并利用图形化电磁暂态仿真工具（Electromagnetic Transients Program-Restructured Version，EMTP-RV）平台对不同扰动大小、渗透率、风速情形进行仿真，验证所提方法的有效性。

1 风电机组频率支撑机理分析

由于同步机组调速器的再热时间系数远大于风电机组频率响应时间，风电机组的调频过程可简化成有功增量附加至降阶系统频率响应模型[23]中，整理出如图1 所示的含风机调频的降阶系统频率响应模型。

图1 中，s为频域微分算子，Δfsys为系统频率偏差，Req为同步机组等效下垂系数，ΔPL为系统功率缺额，ΔPW为风电机组参与调频增发功率，ΔPm为同步机组参与调频增发功率，Km为机械功率增益系数，FHP为高压涡轮功率的一部分，TRH为再加热时间常数，Hsys为系统惯性时间常数，D为阻尼系数[24-25]。系统频率偏差的频域表达式为：

式中：ωn，ζ为中间变量。

对式（1）进行拉普拉斯逆变换，可得含风机调频的系统频率偏差时域表达式为：

式中：t为扰动发生后经历的时间；α，ωr，ϕ为中间变量。

由式（4）可知，系统频率偏差与同步机组调差系数、系统阻尼、风机频率支撑功率密切相关。其中风电机组的阶跃虚拟惯性控制通过减少系统感受的扰动程度参与系统调频，风电机组提供的有功增量越多，系统感受到的等效扰动越小，系统频率最低点改善效果越好。

2 斜坡形SIC控制策略

为有效检测扰动，防止风机调频误动作，根据我国频率允许变化范围设置±0.02 Hz 的调频死区。当频率低于59.98 Hz 时，风机进入调频模式。图2给出斜坡形SIC 功率预设曲线[21]，其中P0为扰动前风机输出功率，ΔPboost为功率恒定阶段增发功率，ΔPUP为转速恢复阶段加速功率，Tboost为功率恒定阶段持续时间，Tdrop为功率线性下降阶段持续时间。扰动初期，风机输出功率在原功率P0基础上提高ΔPboost，在Tboost时间内保持有功出力恒定为系统提供功率支撑，风机处于减速阶段。Tboost后，风机有功出力线性减小至P0−ΔPUP，防止有功出力阶跃降低引起较大的频率二次跌落，减小时间为Tdrop。随后维持功率不变，风机机械功率大于电磁功率开始缓慢恢复转速。当PMPPT大于P0-ΔPUP时，切换为最大功率跟踪（Maximum Power Point Tracking，MPPT）模式恢复转速，其中PMPPT为风机最大功率跟踪模式输出功率。

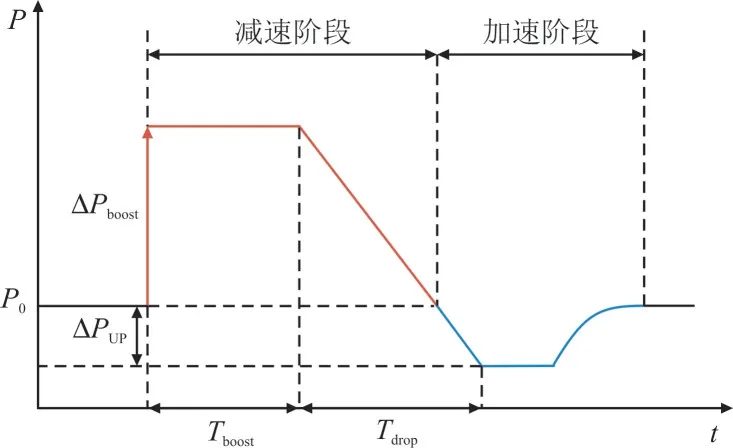
图2 斜坡形SIC功率预设曲线Fig.2 Preset curve for power of ramp type SIC scheme

与传统SIC 不同的是在减速阶段向加速阶段过渡时斜坡形SIC 使功率线性缓慢减小，避免传统SIC 中功率的阶跃下降，减小频率二次跌落。然而斜坡形SIC 参数间的不确定关系使得风机存在失速的隐患。影响斜坡形SIC 调频控制效果的参数有：ΔPboost，Tboost，Tdrop和ΔPUP，表面上看这4 个参数是相互独立的，可以随意设定，但实际上一个参数设定好后，对其他参数的调节范围会有所限制。例如，ΔPboost和Tboost不能同时增大。若两者均较大，则可能过度释放旋转动能导致风机失速。反之，若Tboost较小，那么ΔPboost与ΔPUP过大又会引起频率二次跌落，ΔPUP过小，则转速恢复缓慢。

3 改进斜坡形SIC策略

本文针对转速恢复期间风机失速隐患问题，重点对Tdrop进行深入研究，建立ΔPboost，ΔPUP与Tdrop的数学关系，提出计及风机有效旋转动能的风机转速恢复控制策略。改进斜坡形SIC 策略框图如图3 所示。

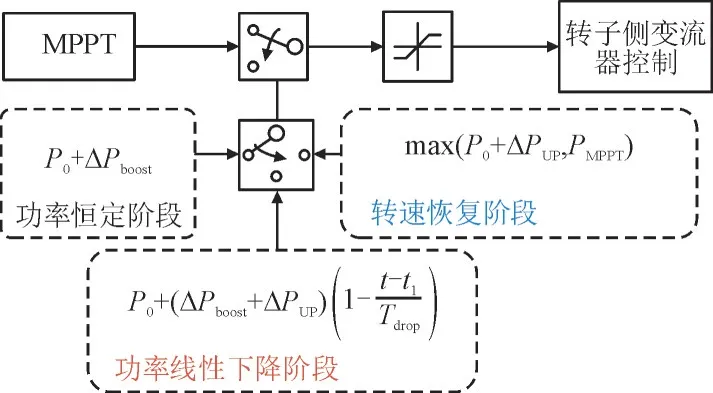
图3 改进斜坡形SIC策略控制框图Fig.3 Control block diagram of improved ramp type SIC strategy

本文在斜坡形SIC 基础上将其减速阶段细分为功率恒定阶段（如图4 中t0至t1段）和功率线性下降阶段（如图4 中t1至t2段）。

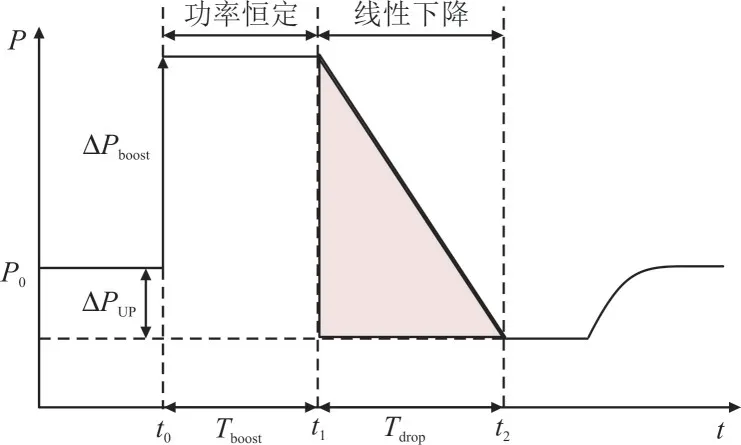
图4 改进SIC方案功率预设Fig.4 Preset curve for power of improved ramp type SIC scheme

在保证频率支撑效果以及功率恒定阶段不会导致风机失速的前提下，确定较小ΔPboost和Tboost。考虑t1时刻风机允许释放的最大旋转动能，对频率线性下降阶段释放的旋转动能（如图4 中涂色部分面积）进行约束，t1时风机有效旋转动能计算公式为：

式中：ΔE为t1时风机有效旋转动能；ωt1为t1时风机转速；ωt2=ωmin,ωmin为风机最小转速限值；H为风电机组惯量时间常数。

功率线性下降阶段释放的旋转动能，即图4 中涂色部分面积，计算公式如下：

由式（8）和式（9）可得：

因为ωt2=ωmin，所以式（10）计算的Tdrop是防止风机失速极值。其他参数不变的情况下，若设置的Tdrop不超过式（10）计算的最大值，则不会出现风机失速。而尽可能大的Tdrop有利于减小频率二次跌落。因此，本文设计的优化方案保留了斜坡形SIC 减小频率二次跌落的优点，同时消除风机失速的隐患。

图5 为改进方案转速域的功率变化曲线，其中ω为风机转带，P为风机相关功率，PM为风机捕获的风功率，Pref为功率轨迹预设功率。扰动发生前稳定在A点，风机工作在MPPT 模式，输入机械功率等于输出电磁功率，Pref=PMPPT=PM。扰动发生后，输出功率增加，运行点变化到B点，Pref＞PM，转子开始减速。BC段为频率支撑阶段，CD段为功率随时间线性降低阶段。在D点，Pref＜PM，转子开始加速。DE段转速恢复，E点切回MPPT 模式。EA段继续恢复转速，回到A点。

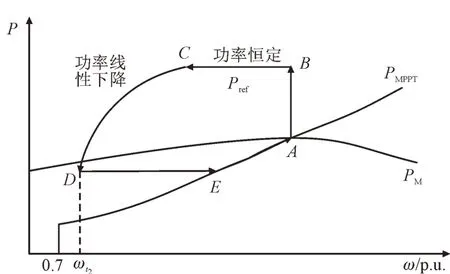
图5 改进斜坡形SIC转速域功率轨迹Fig.5 Power trajectory of improved ramp type SIC strategy in rotor speed domain

值得注意的是改进方案中，转速并不会减小到最小限速值（0.7 p.u.），这是因为在实际运行中功率线性下降阶段释放旋转动能为图4 中P0等值线以上涂色三角形面积，比图4 所示涂色面积小。为简化计算，以图4 涂色面积表示功率线性下降阶段释放的旋转动能，为转速留有一定裕度，避免了转速临界带来的稳定性问题。

4 基于EMTP-RV平台的仿真分析

本文基于IEEE14 节点系统模型在不同扰动、不同渗透率、不同风速情形下对风机不参与调频、斜坡形SIC 以及改进斜坡形SIC 3 种控制方案进行仿真分析比较，验证改进斜坡形SIC 策略的适用性。IEEE14 节点系统模型详见文献[26]。仿真中ΔPboost为0.18 p.u.，ΔPUP为0.05 p.u.。根据电力系统的动态特性和实际经验，频率跌落最低点通常在功率缺额扰动后3～5 s 到达。为保证对频率最低点支撑能力，同时避免释放过多的旋转动能，本文将Tboost设置为4 s。斜坡形SIC 中Tdrop为10 s[21]。不同扰动、不同渗透率算例中风速为7.5 m/s。

4.1 不同扰动下仿真对比

图6 为扰动100 MW、渗透率18.6%时的仿真结果。图6（a）中风机参与斜坡形SIC 和改进斜坡形SIC 时系统频率最低点均为59.10 Hz，比风机不参与调频时提高0.15 Hz，可见斜坡形SIC 和改进斜坡形SIC 都能对频率最低点起到较好的支撑作用。图6（b）中斜坡形SIC 的Tdrop为10 s，通过式（10）计算，改进斜坡形SIC 的Tdrop为8 s，功率下降比斜坡形SIC 更快，在功率线性下降阶段释放更少的旋转动能。由图6（c）转子转速变化曲线可见，斜坡形SIC 在60 s 时释放的旋转动能超出最大值，转速达到最小限速值，出现风机失速现象，在图6（a）中引起严重的频率二次跌落，而改进斜坡形SIC 避免风机失速现象。因此，改进斜坡形SIC 可以消除风机失速的隐患。

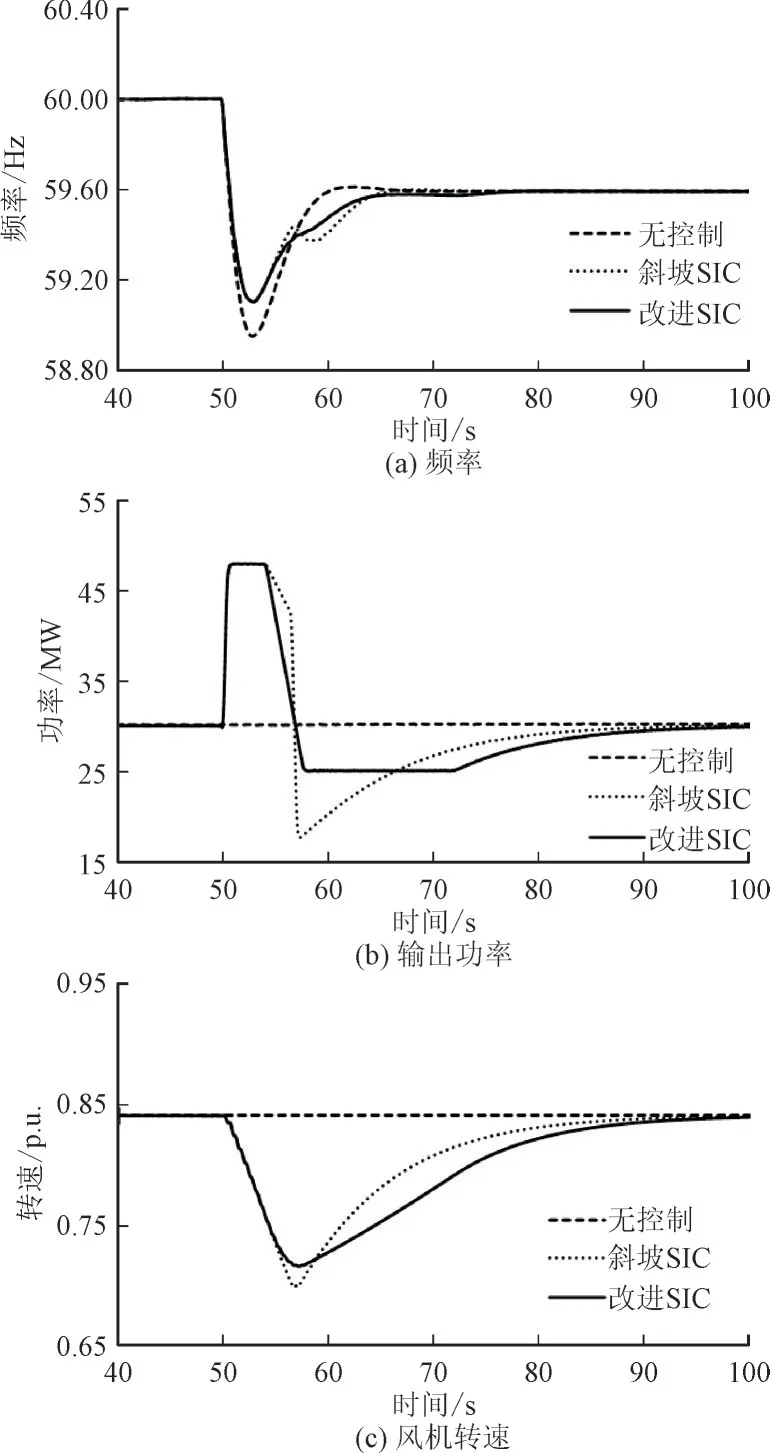
图6 扰动100 MW、渗透率18.6%时的仿真结果Fig.6 Simulation results with both a disturbance of 100 MW and a wind power penetration of 18.6%

图7、图8 给出了扰动为80 MW 和60 MW、渗透率均为18.6%时的仿真结果。

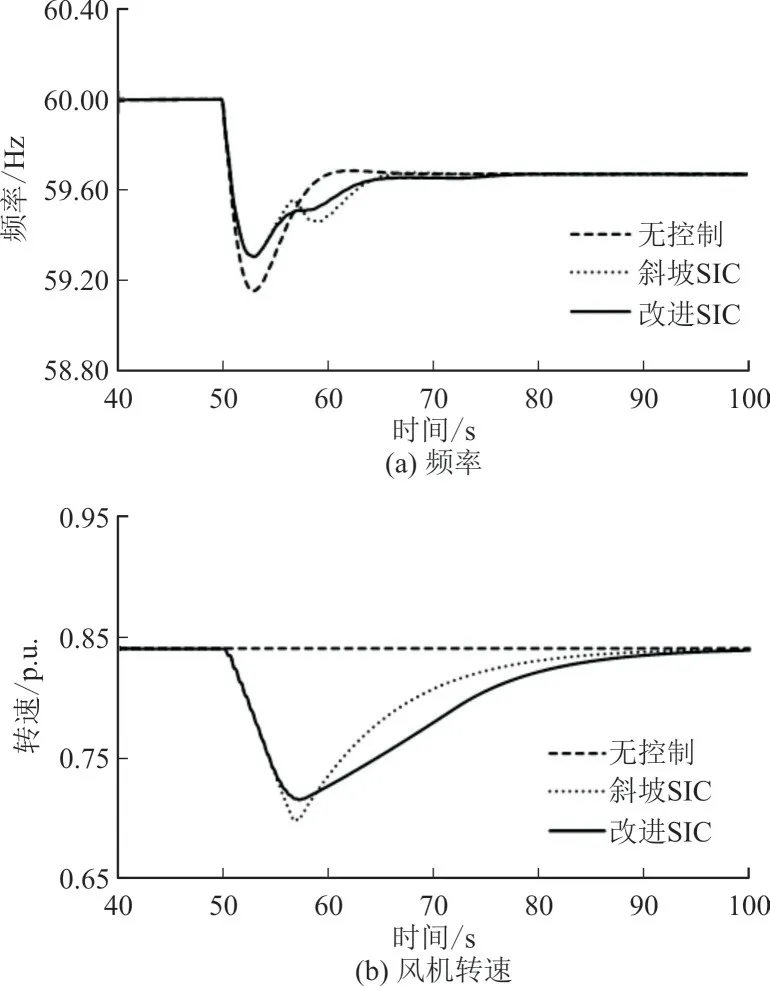
图7 扰动80 MW、渗透率18.6%时的仿真结果Fig.7 Simulation results with both a disturbance of 80 MW and a wind power penetration of 18.6%

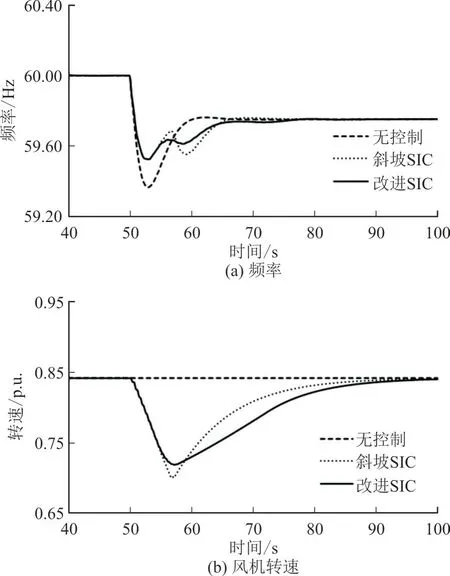
图8 扰动60 MW、渗透率18.6%时的仿真结果Fig.8 Simulation results with both a disturbance of 60 MW and a wind power penetration of 18.6%

由图7、图8 可以看出，80 MW 和60 MW 扰动下斜坡形SIC 和改进斜坡形SIC 都能有效支撑频率最低点。然而斜坡形SIC 在功率线性下降阶段释放更多旋转动能使转速降低至最小限速值，80 MW 和60 MW 扰动下都出现风机失速现象。而改进斜坡形SIC 由于Tdrop比斜坡形SIC 中Tdrop小，能够更快地降低功率，在功率线性下降阶段释放更少的旋转动能，所以80 MW 和60 MW 扰动下均未出现风机失速现象。

4.2 不同渗透率下仿真对比

本文在恒定风速7.5 m/s、扰动100 MW 下设置不同渗透率的仿真算例。图9 为渗透率38.1%时系统频率和风机转速结果。与低渗透结果类似，由于Tdrop的设置不当，斜坡形SIC 出现风机失速现象，引起的频率二次跌落最低点为59.094 Hz，比扰动更加严重，在高渗透率的电网中风机失速的隐患不容忽视，虽然改进斜坡形SIC 引起了一定的二次频率跌落，但是很好地避免了风机失速问题。

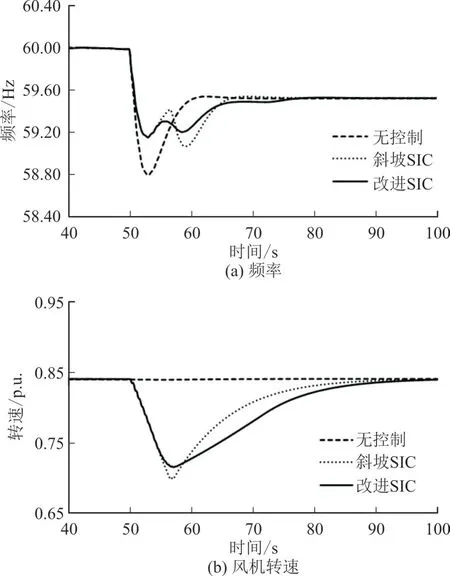
图9 扰动100 MW、渗透率38.1%时的仿真结果Fig.9 Simulation results with both a disturbance of 100 MW and a wind power penetration of 38.1%

4.3 不同风速下仿真对比

本文在风速9 m/s 时设置100 MW 扰动、18.6%风电渗透率的仿真算例，与图6 中7.5 m/s 时仿真形成对比，旨在不同风速工况下验证所提方法的有效性。仿真结果如图10 所示。

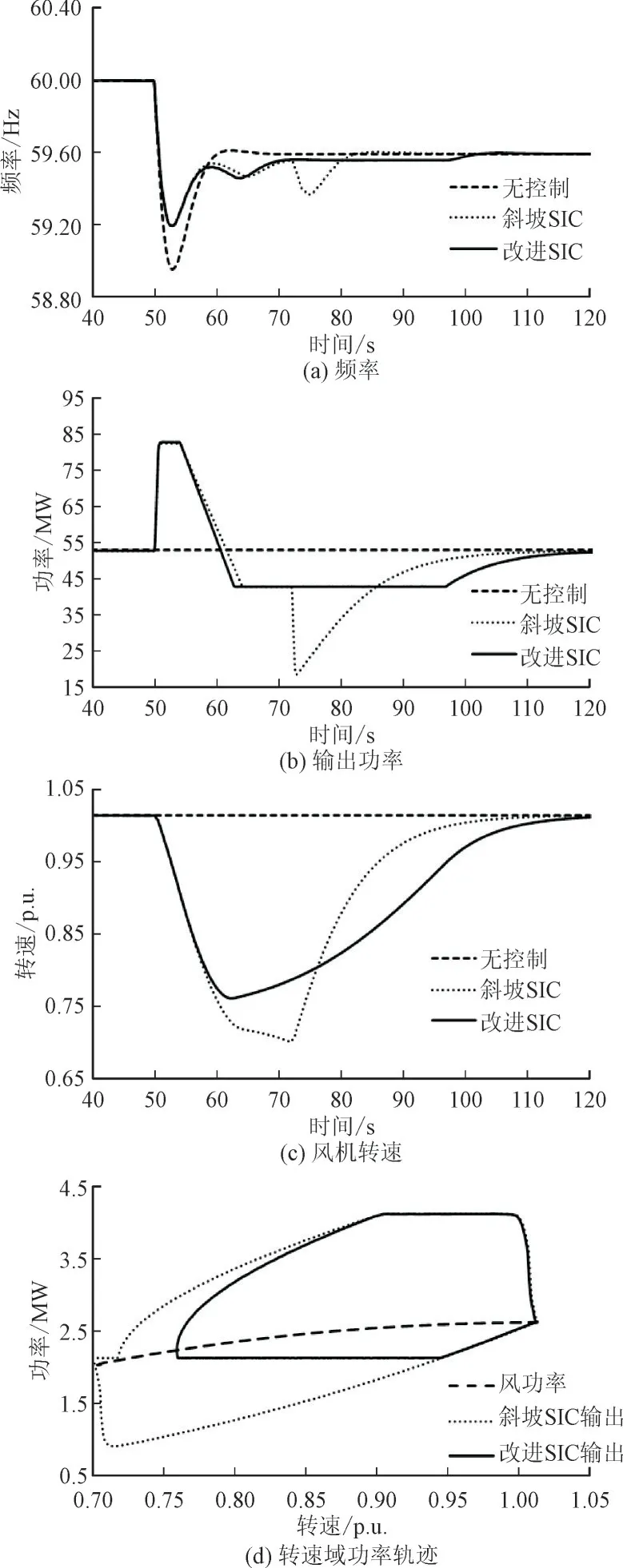
图10 风速为9 m/s时的仿真结果Fig.10 Simulation results with a wind speed of 9 m/s

由于本文所述风机失速问题多发于低风速情况，所以风速9 m/s 时因风机旋转动能较高，图10中斜坡形SIC 并未在功率线性下降阶段出现风机失速现象；然而如图10（d）所示，9 m/s 时风机Pm曲线在低转速区更加陡峭，导致斜坡形SIC 转速恢复阶段初期Pe＞Pm，转速持续降低，在转速恢复初期难以寻找到电磁功率低于机械功率场景，最终引起失速现象，造成严重的二次频率跌落。改进SIC 由于在功率线性下降阶段释放旋转动能较少，转速恢复阶段初期转速高于斜坡形SIC，Pe＜Pm，转速逐渐恢复。因此本文所提改进SIC 在不同风速工况下仍能避免风机失速。

5 结论

本文针对斜坡形SIC 转速恢复期间存在风机失速隐患的问题，提出计及风机有效旋转动能的改进斜坡形SIC 策略，在斜坡形SIC 基础上建立调频期间转速减速阶段增发功率、加速阶段降低功率与功率轨迹线性下降阶段时间的数学关系，对线性下降阶段时间加以约束。经验证，所提控制策略在线性下降阶段释放的旋转动能明显少于斜坡形SIC，同时保证调频效果不受影响，有效预防双馈风机调频期间失速现象。