考虑居民用户可调节潜力的负荷聚合商日前投标决策优化模型研究

2024-02-27刘金朋刘胡诗涵张雨菲邓嘉明胡国松李万鹏

智慧电力 2024年2期

刘金朋，刘胡诗涵，张雨菲，邓嘉明，胡国松，李万鹏

（1.华北电力大学经济与管理学院，北京 102206；2.华北电力大学国际教育学院，北京 102206）

0 引言

随着构建新型电力系统加快推进，大规模可再生能源发展建设与分布式能源穿透能力不断提升，呈现源端供给资源日趋丰富、用端需求负荷灵活多变的发展态势，电源、电网侧的调节资源已难以满足系统安全高效的运行需求，亟须深入挖掘需求侧资源的灵活调节潜力。在需求侧资源中，居民侧柔性负荷资源呈现规模大、响应快、灵活性高的特征[1]，调控作用日益凸显，但其单个容量较小、数量众多、随机性较强，不利于直接参与电力市场交易[2]。负荷聚合商（Load Aggregator，LA）通过整合需求响应（Demand Response，DR）资源参与电力市场调控，一方面聚合居民用户的负荷资源参与DR 市场交易，从而提高居民闲置资源的利用率。另一方面，协助居民用户建立高效合理的用电习惯，从而提升居民用电的高效性，其具有重要的资源耦合与高效利用助推作用[3-5]。

目前，国内关于居民用户与LA 的研究主要集中在调控优化上。文献[6-7]深入阐述了LA 的运营机制和调度策略，详细分析了居民用户与LA 的相互作用。文献[8]引入聚合器提出实时交易响应模型，进行柔性资源的最优调度。文献[9-10]引入非合作博弈理论，分别以最大化LA 利润和最小化投标量偏差为目标，构建了居民日前投标和实时调度的分层模型。文献[11-12]引入主从博弈理论，以最大化LA、分布式电源主体的经济效益和最小化居民用电成本为目标进行经济优化调度研究。文献[6-12]所提出的有关LA 调度优化的策略，都是基于可调节潜力为最大值时所得到的结果，其未考虑影响柔性负荷可调节潜力程度的因素，忽略了用户的用电习惯和用能感受，会导致投标竞价的策略结果有一定偏差。文献[13]基于信息间歇决策理论对用户响应不确定性进行建模，量化LA 收益和风险损失。文献[14]考虑用户调节行为多样性，构建基于用户空调负荷温度控制的LA 日前优化模型。文献[15]基于裕度指标的状态队列优先算法，构建了LA日前经济调度模型，实现部分负荷优先响应。文献[16]基于信用激励机制构建了需求侧激励价格双层优化模型。文献[13-16]所提出的柔性负荷可调节潜力研究，仅考虑了用户的用电舒适度，未考虑用户的响应意愿度，其结果可能会导致LA 参与市场交易有一定的信息偏差，从而影响其实施的精准性。

为此，本文进一步深化居民可调节潜力问题研究，考虑用电物理约束，引入用户响应意愿度和电器用电阈值度，建立居民柔性负荷可调节潜力模型。同时，考虑电力调度与LA 的交互体系，构建基于非合作博弈理论的日前投标优化模型，进行最优投标决策问题研究，推动居民用电调控与LA 运营研究创新拓展。

1 LA参与电力市场主体架构

在本文中，电力市场由电力公司调度部门、LA和居民用户构成。其中，电力公司调度部门通过电网公司所给的历史负荷数据，预测负荷量以获得负荷削峰时段，并将削峰时段的预测负荷量和电价信息参数告知所有参与投标的LA，各LA 通过聚合居民用户的可调节潜力资源，最大化考虑各自的利益进行投标决策，最终将得到的决策结果反馈给电力公司调度部门，电力公司调度部门据此制定调度计划给电网公司，电网公司根据调度计划与售电公司和LA 进行购电。在此过程中，LA 通过对居民可调节潜力资源的分析获得DR 投标竞价资本。LA 参与电力市场进行日前投标决策优化的思路框架如图1 所示。

图1 LA参与电力市场进行日前投标决策优化的思路框架Fig.1 Framework of thinking for optimization of dayahead bidding decision by LA in electricity market

2 居民柔性负荷可调节潜力分析模型构建

2.1 可调节负荷分类

LA 作为连接中小型电力用户、电力市场的中间机构，应在考虑DR 的基础上，选择居民常用的高耗能用电设备进行负荷聚合，即形成动态可控负荷。动态可控负荷是指在一定的调控策略下可以灵活控制、快速调整的用户侧负荷[17]。本文在此将其分为三类：可中断可平移负荷，可中断不可平移负荷以及不可中断可平移负荷[18]。

可调节负荷Ⅰ：指可中断可平移的负荷类型，用户对该类负荷的需求主要集中在最终用电总量上，如电动汽车（Electric Vehicle，EV），只需在用户出行前达到用户所需的充电量即可满足用户需求。因此，本文以EV 为研究对象，考虑其行程所需负荷的可接受状态阈值，引入用户舒适度和用电习惯，得出可调节负荷Ⅰ的可调节潜力模型。

可调节负荷Ⅱ：指可中断不可平移的负荷类型，用户对该类负荷的需求主要集中在使用时段上，如洗衣机（Washing Machine，WM）、洗碗机等，只需在用户规定时段内完成相应任务即可满足用户需求[15]。因此，本文以WM 为研究对象，考虑其用电时间段的可接受调节阈值，得出可调节负荷Ⅱ的可调节潜力模型。

可调节负荷Ⅲ：指不可中断可平移负荷的负荷类型，用户对该类负荷的需求主要集中在使用温度上，如空调（Air Conditioning，AC）、电热水器等温控设备，只需根据用户设定的温度区间进行调控，就会减小对用户的影响。因此，本文以AC 为研究对象，在保证用户体感舒适度的前提下，考虑最大降负载能力，得出可调节负荷Ⅲ的可调节潜力模型。

2.2 用户响应意愿度

为了量化用户参与DR 的积极性，本文引入用户响应意愿度作为指标，通过考虑用户对电价的敏感性，来衡量用户的响应意愿度。

以当前用电价格pnow与用户预期用电价格pexp进行比较，若pnow高于pexp，则当前用电成本过高，为了降低用电成本，用户愿意协调用电计划，通过调节用电量的方式来参与DR，以获取补贴来弥补用电舒适度下降的结果；若pnow低于pexp，则当前用电成本不高，为了保障自身用电舒适度，用户不太愿意过多改变用电计划，参与DR 的意愿度较低。同时，居民用户对价格敏感程度还与其自身异质性有关。其中，受教育程度高以及年轻的用户对电价波动较敏感，认为补偿费用能够弥补用电舒适度下降的损失，容易接受新事物，参与DR 积极性较高；而高收入家庭对用电舒适度更注重，认为补偿费用不能弥补用电计划变动带来的损失，其参与DR 积极性较低。综合考虑用户对电价敏感程度的影响因素，设定用户响应系数φ，反映用户对电价的敏感程度和响应意愿。

2.3 典型电器用电阈值度

2.3.1 EV负荷用能阈值度

本文将EV 负荷分为离网和在网两种充放电状态，离网包括早间时段上班行程和晚间时段下班行程，在网包括早间时段和晚间时段[19]。考虑EV 用户的用能诉求，可知其能否参与负荷调节与每次出行所需的荷电状态阈值SOCth相关[20]，同时，为防止特殊情况如堵车等带来的电能消耗，要求每次出行的荷电状态不能低于出行状态阈值S′OCth。

式中：l为EV 出行的距离；L为EV 的最大设计续航里程；τ为出行阈值度，本文中取τ=5%。

用户响应意愿度可影响EV 用户的在网充放电时间，当pnow＞pexp时，EV 用户在网放电概率高，可接受出行状态阈值降低；当pnow＜pexp，EV 用户在网充电概率高，可接受出行状态阈值增高。在此引入用户用能阈值度，对在网和离网2 种状态下EV 不同荷电状态情况进行讨论：

1）若EV 在网后可进行放电调度，并在调度结束后开始充电直至离网而不影响出行计划，则该用户的用能阈值度较高，EV 具有放电可调节潜力。定义第iEV辆EV 在放电调节后离网时刻的荷电状态为

式中：tdis为放电调节开始时刻；tend为调节结束时刻；tout为离网时刻；α为充放电效率，本文中取α=0.9；B为EV 的电池容量；WEV为EV 的额定功率。

2）若EV 在网后不能进行放电调度，则该用户的EV 负荷用能阈值度一般，仅能进行正常充电行为，EV 具有充电可调节潜力。定义第iEV辆EV 在充电调节后离网时刻的荷电状态为。

式中：tcha为充电调节开始时刻。

由这2 种情况可得出第iEV辆EV 的充、放电可调节潜力

（1）离网状态的充放电可调节潜力：

（2）在网状态的充放电可调节潜力：

当EV 荷电状态高于可接受出行状态阈值时，EV 负荷可进行放电调度，其可调节潜力为负值，反之，EV 负荷进行充电调度，其可调节潜力为正值。因而，聚合区域内t时刻EV 总数nEV的负荷充、放电可调节潜力分别为APEV_cha(t)，APEV_dis(t)：

2.3.2 WM负荷时间阈值度

本文结合用户用电习惯得出WM 负荷的使用开始、停止时刻分别为tWM_s，tWM_e，在此考虑可接受调节阈值得到使用时间。从中可看出考虑用户响应意愿度，可扩展用户WM 负荷的使用时间段，则聚合区域内t时刻全部WM 的负荷可调节潜力APWM,t为：

式中：nWM为聚合区域内WM 总数；WWM为WM 的额定功率；为t时刻第iWM个WM 的工作状态，其为0～1 变量，当xiWM=1 时为洗衣机正在工作，当=0 时为洗衣机停止工作。

2.3.3 AC负荷温度阈值度

单台AC 最常见的物理模型为ETP 模型[21]，一阶ETP 模型采用一阶常微分方程来描述室温的变化，为得到第iAC个AC 的开机周期Ton,iAC和停机周期Toff,iAC，对一阶常微分方程进行求解，得到结果如下：

式中：C为房间等效热容；R为房间等效热阻；Q为AC 的制冷/制热功率，与AC 用电功率WAC存在关系Q=μWAC，其中μ为AC 能效比；θout为t时刻的室外温度；θset为AC 温度设定值；θset+δ/2，θset-δ/2 分别为AC 正常运行状态下室内温度上、下界值，其中δ为AC 的温度死区宽度。

一般情况下，单台AC 的平均用电功率受AC使用时间和室内外温差的影响，反映到AC 中的具体表现为开机周期不同，利用占空比可知其处于开机状态的概率MAC_on,iAC为:

由文献[22]可知，利用近似聚合模型的聚合功率估计值与实际值相差误差低于5%，因而可根据大数定律，获得nAC个AC 的聚合功率WAC_sum()t为：

式中：WAC,iAC为第iAC个AC 的用电功率。

将式（11）代入式（13），并通过高等数学的不等式变化，获得nAC个AC 聚合功率的上界和下界

由式（15）可知，集群AC 的最大降负荷能力仅由当前时刻室外温度与空调温度设定值决定。为评估AC 对用户满意度的影响，在此引入FangerPMV 热舒适模型，由文献[23]可知，当温度为26 ℃时，PMV 值接近于零值，舒适度最高，而根据ISO7730 给定PMV 的取值可知，在PMV 为±0.5 时用户处于最佳舒适度状态，此时相应室内温度为24.8 ℃～27.3 ℃，将其设定为初始温度可调节裕度。

3 基于非合作博弈的LA 日前投标决策优化模型构建

3.1 LA日前投标决策模型构建

LA 基于所获取的削峰时刻负荷预测信息以及电价信息参数，制定日前投标竞价策略。假设共有NT个时段需要削减负荷，有NLA个LA 进行投标竞价参与DR。电力公司按照各时段t∈T(T={1,2,...,NT})的总体负荷削减量Lst和市场价格pt向LA 支付购电费用，其中，所有LA 在时段t的总体负荷削减量Lst为:

式中：Lst,nLA为第nLA个LA 在时段t的削减量，nLA∈N(N={1,2,…,NLA})。

市场价格与负荷水平呈显著的线性关系[24]：

式中：Lt为LA 在时段t的预测负荷量；为价格负荷系数；为常数项，均由电价历史数据通过拟合而得，其中

当确定LA 削减量和市场价格后，可计算得出各个LA 在时段t内从电网调节部门获得的收益为PtLst,nLA。LA 通过与用户签订合同，以补偿费用换取负荷调节权，设λiLA(iLA=1,2,3)为负荷的补偿费用，且满足λ1＜λ2＜λ3。设第nLA个LA 的负荷削减量中3种负荷分别为，则LA 在时段t给用户的补偿费用为。LA 进行投标时，以最大化自身利润Zpro为目标进行投标决策，即：

2.1 基本情况发生排斥反应34例34眼，男29例，女5例，年龄14～81岁，平均(50.45±13.26)岁，出现排斥反应时间为术后(1.65±3.25)个月。

3.2 LA非合作博弈模型

由式（17）可知，LA 的利润不仅受到自身投标量Lst,nLA的影响，还与其他LA 的投标量有关，即LA 的最终决策会受其他参与者决策行为的影响，由此可知LA 的日前投标决策过程属于非合作博弈[25]：

1）参与者：所有参与电力市场交易，进行日前投标竞价的LA，nLA∈N(N={1,2,...,NLA})。

2）策略集合：参与投标竞价的LA 上报至电网调节部门的负荷削减量Lst,nLA。

3）收益函数：LA 的削峰时段总利润Zpro，即：

式中：RnLA为第nLA个LA的策略集；为第nLA个LA 在时段NT内的投标策略；为除nLA以外NLA-1个LA 的投标策略。

所有非合作博弈的参与者以追求自身利润最大化为目的，在与其他参与者博弈竞争时，不断调整自身投标策略，当任意参与者达到都不会改变投标策略的状态时形成了纳什均衡，则该决策集合为纳什均衡点：

4 LA日前投标决策优化模型算例分析

4.1 算例基本场景

4.1.1 居民用户及响应意愿度

假设某地区有15 000 个居民用户，每个用户配备1 个EV，WM 和AC，假设该地区共有3 个LA，均衡管辖该地区用户，即每个LA 拥有5 000 个用户。假设区域1，2，3 用户的DR 参与率分别为0.90，0.80 和0.70。以夏季晚上18：00—次日6：00 为调控周期进行算例分析，调节颗粒度为15 min，共48个时段。

1）居民用户分类。基于《中国统计年鉴2022》数据，利用Matlab 进行数据仿真模拟，结合式（3）得出响应系数，通过数据标准化处理后，对居民进行聚类分析，采用Calinski-Harabasz 指数，确定最佳的分类组数为4。其中，家庭平均收入I分布呈现双峰状态，适合混合高斯模型；家庭平均年龄A和家庭受教育程度E呈现随机分布，最终聚类结果如图2 所示。

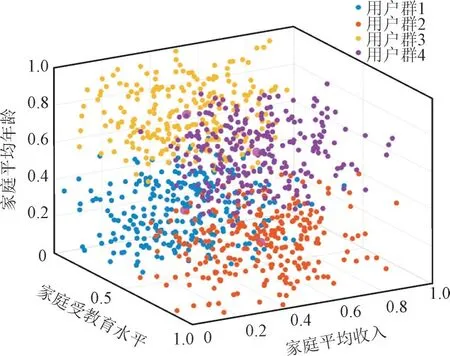
图2 居民用户聚类分析Fig.2 Cluster analysis of resident users

2）用户响应意愿度。基于图2 的居民分类，以分时电价中平时段的电价作为用户预期电价，通过式（1）可计算得出各时段用户参与DR 的响应意愿度如图3 所示。

图3 居民用户参与DR意愿度分布情况Fig.3 Distribution of willingness of resident users to participate in DR

在0：00—6：00 时段，电价低于用户预期电价，用户对DR 态度消极，其可调节范围缩小，EV 充电响应潜力高，WM 可使用时段缩短，AC 温度不愿被过多调节；在6：00—10：00，15：00—18：00，22：00—24：00 时段，电价等于用户预期电价，用户参与DR意愿处于中立状态；在10：00—15：00，18：00—22：00时段，电价高于用户预期电价，用户对DR 态度积极，其可调节范围扩大，EV 放电响应潜力高，WM 可使用时段增长，AC 温度可适当调高。

4.1.2 LA负荷聚合商

4.2 仿真结果及分析

1）考虑可调节潜力的典型用电电器响应结果。根据式（9）获得各区域EV 负荷18：00—次日6：00时段的可调节潜力，如图4（a）所示。其中，当可调节潜力为正值时，用户有响应潜力，可进行负荷调节；反之，需要LA 将负荷转移到此时刻。同时，EV负荷的可调节潜力符合用户响应意愿度，在18：00—24：00 时段，用户参与DR 的态度积极，其放电响应潜力高，在21：00 时刻左右放电可调节潜力达到最大值，此刻区域1，2，3 的可调节潜力分别为11.782 0 MW，10.678 5 MW，9.497 0 MW；在1：00—6：00时段，用户参与DR 的态度消极，其充电响应潜力高，在4：00 时刻左右充电可调节潜力达到最大值，此刻区域1、2、3 的可调节潜力分别为-10.043 5 MW，-8.656 5 MW，-7.310 0 MW。

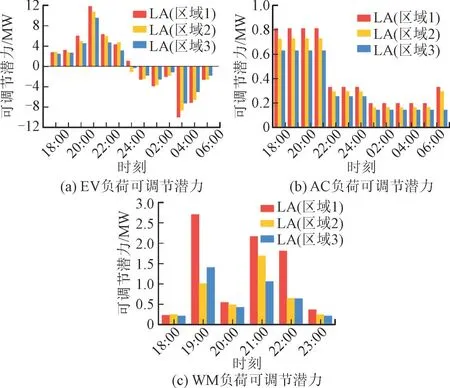
图4 各LA的EV，AC和WM负荷可调节潜力分布情况Fig.4 Adjustable potential distribution of EV，AC and WM load for each LA

根据式（15）和式（10）可获得各区域AC 负荷18：00—次日6：00 时段的可调节潜力和WM 负荷18：00-23：00 时段的可调节潜力，分别如图4（b）、图4（c）所示。对于AC 负荷，当用户响应意愿处于消极时段，温度可调节范围小，区域1，2，3 的可调节潜力分别为0.195 3 MW，0.160 7 MW，0.140 8 MW；当用户参与DR 意愿处于中立时段，温度调节需满足用户体感舒适需求；当用户响应意愿处于积极时段，区域1，2，3 的可调节潜力分别为0.811 5 MW，0.726 8 MW，0.629 5 MW。对于WM 负荷，WM 的使用时间一般为17:00—22:00 时段，考虑可调节响应系数，导致部分使用时间延伸至18：00—23：00 时段。

同时，对比3 种负荷的可调节潜力，明显看出在相同条件下，EV 负荷的可调节潜力大于AC 和WM 负荷，这是因为前者对电价敏感，而后者中AC负荷直接与用户用电舒适度有关，需长时间处于工作状态，而WM 负荷直接与用户使用时间有关，开启后不可暂停。

2）基于非合作博弈的日前投标决策。在求得3 个LA 的EV，AC 和WM 负荷可调节潜力后，利用非合作博弈理论求解最优投标策略，得到各LA 在18：00—次日6：00 时段内的计划削减负荷量。其结果如图5 所示。

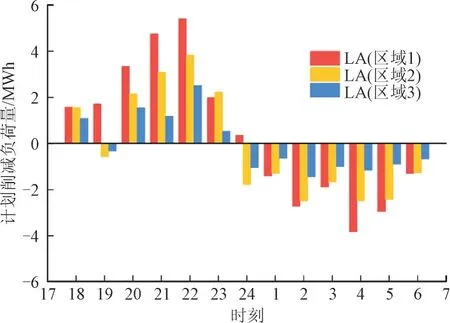
图5 LA各时段负荷削减量分布情况Fig.5 Distribution of load curtailment of load aggregator in each period

3 个区域内的LA 总计划削减量从18：00 时刻的4.192 3 MWh 下降至19：00 时刻的3.798 3 MWh，之后逐步上升至22：00 时的11.734 5 MWh，削减量与电网预测的峰时段负荷曲线趋势一致，验证了该模型的可行性。从图5 中还可看出，LA 的负荷调节潜力和用户DR 参与率与其投标量成正比，例如，区域1 的用户DR 参与率最大，大部分时间段的投标量较大；而区域3 的用户DR 参与度最小，大部分时间段内的投标量较小。

因此，将电力交易市场中的现货价格引入LA竞标决策中，可以有效激励LA 进行博弈和竞争。

3）LA 参与响应前后对比。经过LA 的投标决策后，得到各时段的负荷削减总量，其调节后的负荷曲线如图6 所示。结合图5 可知，当可调节潜力为正值时，LA 具有降负荷的作用；当可调节潜力为负值，LA 具有负荷调节的作用。

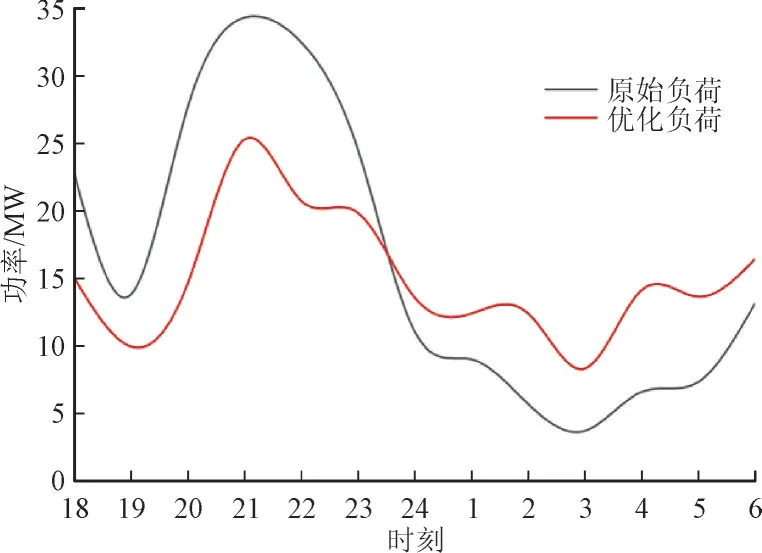
图6 优化前后用电负荷对比Fig.6 Comparison of power load before and after optimization

为了更好地展现LA 参与响应后用电负荷的变化，在此引入峰谷差、峰谷差率、平均负荷、负荷率4个参数进行描述，其结果如下表1 所示。

表1 优化前后用电负荷参数对比情况Table 1 Comparison of power load parameters before and after optimization

由表1 可知，优化后的负荷峰谷差降低，峰谷差率减小，而平均负荷变化不大，说明LA 在电力市场中参与DR，具有较好的削峰填谷效果；同时，优化后的负荷率增大，其设备利用程度提高，能较好地聚合零散用户侧资源。

同时，为了验证本文提出的考虑用户可调节潜力的LA 日前投标决策优化模型的有效性，在此进行负荷调节潜力为额定功率10%的投标策略对比，用电满意度通过文献[26]的方法获取。对比结果如表2 所示。

表2 LA利润与用户用电满意度对比情况Table 2 Comparison of LA profits and users’power consumption satisfaction

从表2 可看出，未考虑用户可调节潜力的LA总利润会高于本文提出的考虑可调节潜力的LA 的总利润，这是因为在未考虑用户可调节潜力的场景下，LA 会以自身的利润最大化为目标进行投标，因而其利润较大，但两者相差不大。但是，未考虑用户可调节潜力的用电满意度远低于考虑用户可调节潜力的用户用电满意度，这是因为在考虑用户可调节潜力的场景下，将用户响应意愿度和电器用能阈值度作为重要因素进行研究，可以提高其满意度。

综上所述，本文在兼顾LA 利润的同时加强对用户满意度的考虑，其LA 日前投标决策优化模型更加合理性和精准性，具有一定的实际参考意义。