基于连接状态定位的智能变电站二次系统故障定位方法
2024-02-27杨家全王志明潘振宁
李 远,苏 适,杨家全,王志明,潘振宁
(1.云南电网有限责任公司红河供电局,云南蒙自 661100;2.云南电网有限责任公司电力科学研究院,云南昆明 650217;3.南方电网数字电网集团有限公司,广东广州 510000;4.华南理工大学电力学院,广东广州 510640)
0 引言
智能变电站二次系统是监测智能变电站状态、保障变电站安全稳定运行、调整运行方式的重要部分,可将变电站全站信息统筹规划实时监测显示,有利于变电站值守人员对变电站状态的整体把握。随着智能变电站的发展以及智能电子设备的投入运行,智能变电站与传统变电站相比,在结构与设备方面均有较大差异。一方面负荷的快速变化会导致电压、电流等二次系统参数发生变化,另一方面风电和太阳能发电等可再生能源的波动性较强,也会对电力系统的二次设备产生压力,这些不确定性因素,使二次设备长时间处于极限值附近运行[1-5],使得二次系统出现故障的概率增加。因此,为了保证电网的稳定性与安全性,需要进行二次系统的故障搜索定位,在出现故障时可以迅速判断故障种类与故障设备位置,在进行二次设备检修时状态评价结果可提供参考。随着电气二次回路模型化、数字化技术的发展,二次系统信号溯源及搜索定位将具有更加可行的技术基础。
智能变电站二次系统中存在大量智能电子设备,并且同一智能电子设备中一般包含多个逻辑节点,由此带来的海量数据有利于对状态的准确掌握与故障准确定位,同时也导致故障搜索定位面对的数据规模更大,搜索定位难度较大[6-7]。
在传统变电站二次系统故障定位方面,往往采用人工建模、枚举的方法,工作量庞大且复杂。文献[8]采用举证表,依据二次系统通信链路交叉的特点穷举出网络故障的范围,虽然操作简单,但仅适用于二次系统节点数量较少的情况,并且故障诊断范围和精度有限。文献[9]通过二次设备与告警信号间的关联建立故障树,依据故障特征和关联告警信号反向推理故障范围,针对单个故障有较高诊断精度,但无法同时处理多个告警信号。
因此,不少学者将人工智能技术与故障诊断方法相结合,以有效提高故障识别精度,减少故障误判概率。文献[10]针对二次系统中保护设备的隐性缺陷,利用保护设备中信号传递的逻辑关系构建解析模型,通过粒子群算法优化目标函数实现隐性故障的检测。文献[11]利用图论思想,将配电网中各设备视为逻辑节点,通过建立连接矩阵描述其实际连接关系,在此基础上分析实际案例中各设备的故障因果关系,得到改进矩阵判据,采用矩阵算法对故障进行快速搜索与定位。文献[12]利用深度置信网络对故障状态特征进行提取,搭建二次回路故障诊断模型,能快速识别并定位故障范围。
本文提出一种基于连接状态定位的智能变电站二次系统故障搜索方法,通过将系统的物理和通信连接关系转化为一个矩阵模型,其中每个节点的状态信息作为矩阵的元素。利用这一模型,运用矩阵算法来识别系统中的故障节点。随后,结合模糊径向基(Radial Basis Function,RBF)神经网络,该方法可将故障节点与预先定义的故障模式相匹配,从而实现精确的故障定位。这种方法在故障定位方面具有高度的准确性,为智能变电站的维护和运营提供了一种高效且可靠的解决方案。
1 二次系统连接状态矩阵描述
智能变电站二次系统是物理设备和信息数据的融合系统,设备间不仅具有复杂的实体连接关系,同时也具有复杂的通信网络关系及数据交互方式。利用连接状态矩阵可以描述设备间的实体连接关系,同时通过矩阵元素与二次系统设备节点状态量的映射关系可将运行数据融合进矩阵模型,整体描述二次系统的物理-信息融合模型。
1.1 矩阵元素与二次系统设备节点状态量的映射关系
连接状态矩阵将实体设备连接关系与二次系统信息数据融合的基础是矩阵元素与二次系统设备节点状态量的映射关系。通过提取变电站配置描述文件(Substation Configuration Description,SCD)信息可得到矩阵元素与二次系统设备节点状态量的映射关系及二次系统设备节点状态量的取值[13-15]。基于一致性原理将二次系统信息数据与矩阵元素进行映射,矩阵元素坐标与信息传递的源头和终点对应,实现二次系统的故障定位及保护动作监测[16]。矩阵元素通过二次系统的相关二次系统设备节点状态量,描述二次系统设备间的连接状态及设备情况等数据信息[17-19]。根据SCD 文件描述设备状态值的种类,确定矩阵元素类别、取值及表示内容如表1所示。
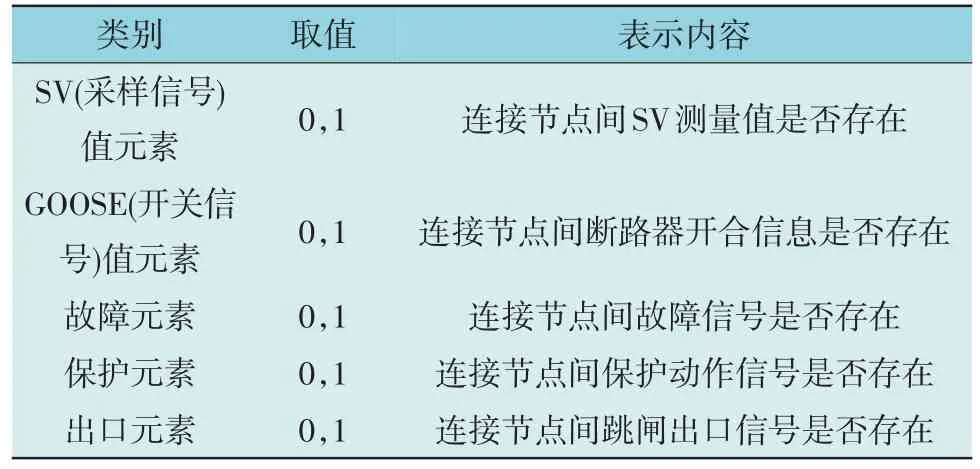
表1 矩阵元素类别、取值及表示内容Table 1 Matrix element categories,values,and representations
SV 值元素取1 表示2 个连接设备中对应连接节点的电压/电流SV 值能够从前一设备的i节点传入后一设备的j节点;取0 表示监测电压电流值消失。GOOSE 值元素取1 表示2 个连接设备中对应节点存在GOOSE 开关量通信,开关量可以从前一设备的i节点传入后一设备的j节点;取0 表示2个设备间GOOSE 通信故障。故障元素取1 表示前一设备i节点发出故障信号,后一设备j节点接收到故障信号;取0 表示无故障信号通信传递。保护元素取1 表示保护设备中节点i发出保护动作信号传递给后一设备的j节点;取0 表示未发出保护动作信号。出口元素取1 表示有跳闸出口、出口压板等信号从前一设备i节点传入后一设备j节点;取0表示无跳闸信号传递。
1.2 连接状态矩阵
静态配置描述文件信息中主要包含了变电站的基础设置[20-21]。对于智能电子设备,有对自身设备状态进行监测的各二次系统设备节点状态量,对与其连接设备进行监测的二次系统设备节点状态量,以及对通信网络进行监测的二次系统设备节点状态量,因此1 个智能电子设备往往需要连接状态矩阵中的多个元素进行描述,即1 个智能设备中可能存在多个节点。以节点为基础构建连接状态矩阵Α,节点数为N,矩阵形式如式(1):
式中:a1N为节点1 和节点N间的连接情况;1 为节点间数据传输正常;0 为节点间数据传输异常。
则有:
式中:m为智能变电站二次系统中智能电子设备的数量;nk(k=1,2,…,m)为第k个智能电子设备包含节点数。
矩阵元素的初始取值根据节点描述及其对应配置描述文件确定。
1.3 连接状态搜索方法
当二次系统状态变化时,节点连接情况也会发生变化,数学上表现为矩阵元素值发生变化,即连接状态矩阵由A变为新的矩阵A*。矩阵A*可以反映二次系统的某种故障,通过对矩阵A*进行解析分析,可对智能变电站二次系统故障进行定位,确定故障范围。
设故障节点数为q(1 ≤q≤limitu),则二次系统故障时有:
式中:aij为q个故障节点对应的矩阵元素;limitu为故障节点的数量上限。
根据相关故障案例及运行经验一般limitu值不超过3。
得到能够表明故障状态的矩阵A*后,利用基于连接状态推理的搜索方法,对故障位置进行搜索。
2 个节点间信号数据传输只经过1 条传输线,没有经过设备中转,这样的节点影响为直接连通。例如二次系统保护设备故障,通过相应节点向出口节点发送错误跳闸出口信号。则直接连通关系中,相应矩阵元素变化可用式(4)描述:
式中:S为二次系统前一状态向量;S′为计算状态改变后的二次系统后一状态向量。
根据智能变电站配置文件确定二次系统初始状态向量S0:
式中:si为二次系统状态向量中i节点的分量。
对初始状态向量进行多次矩阵乘法运算以表示对二次系统连接状态的搜索过程。在二次系统信息传递过程中,对二次系统变化状态进行多次搜索,得到节点的终状态。通过将多次搜索过程后的结果向量相加得到终状态Se:
式中:S′p为第p次状态搜索后,二次系统节点状态向量;sign为符号函数,表示对向量中每一元素进行运算。
通过计算得到终状态向量Se后,对计算结果进行验证。通过状态解析计算将状态向量转化为数值结果,状态解析结果包含了各节点报文数据、接收信息等,将状态解析结果与实际故障后状态结果进行比较,可验证计算状态搜索结果。验证正确后,根据终状态向量Se定位故障节点位置。
状态解析结果d为:
验证说明连接状态搜索矩阵A和故障后的矩阵A*有效后,可进行二次系统的故障定位。设第b个节点在矩阵中元素的行坐标与列坐标分别为xb,yb,则A矩阵与A*矩阵中差异元素集合可表示为:
式中:c为差异元素总个数。
其中,(xb,yb)为第b个差异元素在两矩阵中位置为xb行yb列,确定x节点与y节点两者连接线路为故障区域。
综上,利用输入的初始状态向量、连接状态矩阵A及故障后矩阵A*,可得到二次系统故障后各节点的状态情况,并利用矩阵元素差异实现故障的搜索与定位。具体步骤如图1 所示。其中,Sn-1和Sn为n-1 次和n次搜索过程后的结果向量。
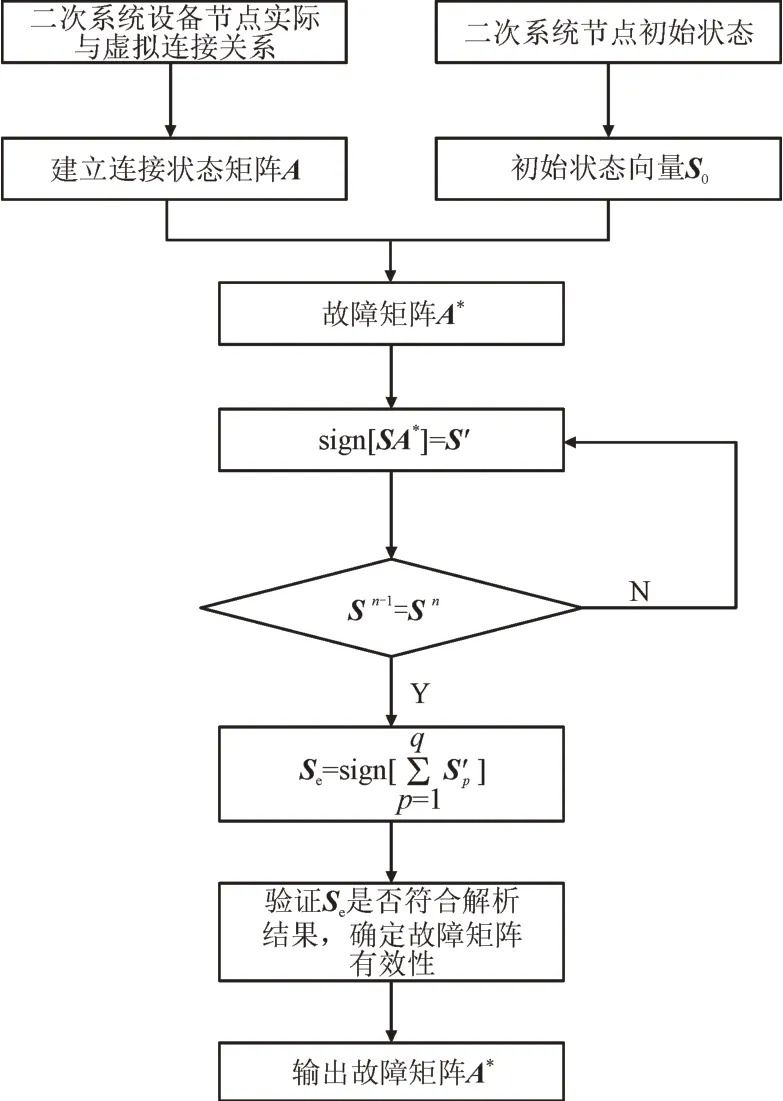
图1 故障的搜索与定位步骤Fig.1 Fault searching and locating steps
2 利用模糊RBF 神经网络优化的故障定位方法
2.1 模糊RBF神经网络模型
单纯利用连接状态矩阵对连接状态进行搜索,计算量较小,但不能综合利用各节点的状态信息。本文在连接状态搜索基础上,利用模糊RBF 神经网络对故障定位进行进一步修正,以更好地理解和解释系统中的故障情况和位置,使故障定位更加准确[22-24]。
RBF 神经网络是一种前馈型神经网络,具有全局逼近能力,相比于BP 神经网络,拓扑结构更加紧凑,网络参数可进行各自独立学习,收敛速度更快。将RBF 神经网络与模糊理论相结合,使单元处理计算简单,计算速度加快[25-27]。
2.2 输入样本编码
2.1 节中神经网络的输入为通过连接状态搜索得到的可疑故障节点坐标,为了简化神经网络计算,将位置坐标进行预处理转化为二进制编码数据序列。
以三维连接状态搜索矩阵A为例,则式(9)中坐标为:
将横纵坐标转化为二进制并将故障类型用二进制表示,本文选取3 种故障类型,编码分别为01,10,11。
将网络输入输出转化为编码形式,可简化神经网络的计算,并且无需进行归一化处理。另外,为了统一输入编码长度,在A*数量不一致时,在输入编码尾端补充0 位,对于三维方阵,其故障节点数最多为2,则输入序列长度统一为24 位编码序列。部分样本案例如表2 所示。

表2 坐标样本案例Table 2 Case for coordinate samples
2.3 故障搜索定位方法流程
将利用连接状态矩阵搜索的疑似故障位置结果输入模糊RBF 神经网络,以神经网络输出端结果作为故障搜索定位的最终结果。故障搜索流程如图2 所示。
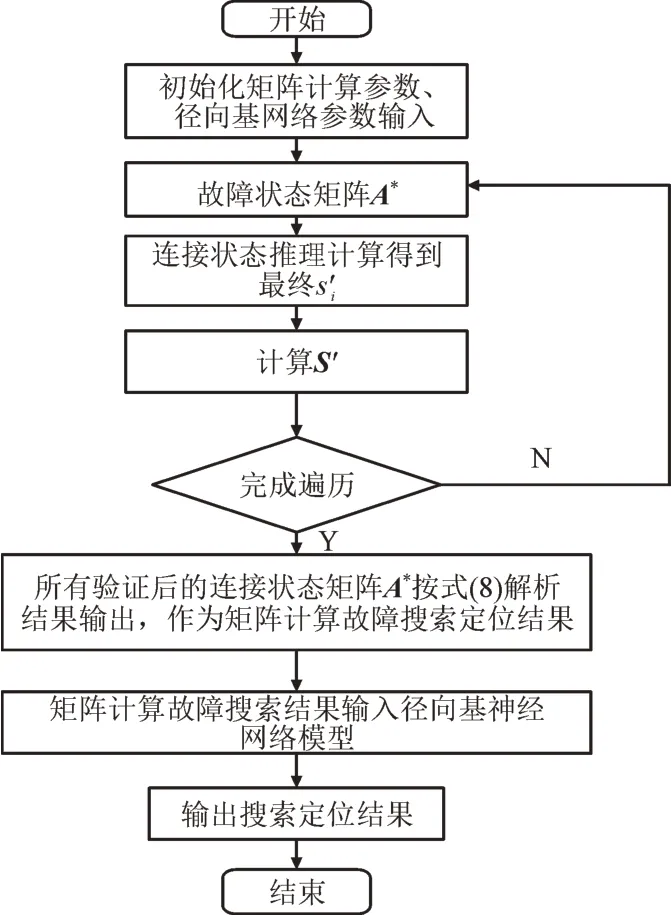
图2 故障搜索流程Fig.2 Process of fault search method
3 算例分析
以如图3 所示的500 kV 线路开关误动案例为例,利用Matlab 编程实现故障搜索定位。其中,0012 为连接开关,0001 和0002 为断路器。WG-Ⅰ线受外部影响发生电压电流突变,导致GY 线上断路器0001 跳闸,造成电网解列与大规模停电故障。检修时将断路器0001 再次闭合,对WG-Ⅰ线进行试送电,断路器0001 再次跳开。GH 站线路保护配置如表3 所示。

图3 故障案例线路运行方式图Fig.3 Line operation of fault case
外部影响出现前,WG 线与GY 线均处于正常运行状态,断路器0001,0002 及连接开关0012 均处于闭合状态。
受波动影响首次跳闸时,WG 线线路主保护1、主保护2、备用保护均无GOOSE 报文,故障录波器未录下波形。0001,0002 断路器保护跳闸失灵开入动作。0001,0002 断路器继电箱跳闸指示灯1 的A,B 两相指示灯点亮。由此,判断跳闸GOOSE 信号来自GY 线线路主保护1 或线路主保护2。
为了查明故障原因,排除暂时性故障影响,在对WG-Ⅰ线主保护1 进行检查后,退出后备保护功能,再次闭合0001 断路器对WG-Ⅰ线进行送电,并再次出现跳闸现象。再次跳闸后,同样无动作GOOSE 信号,故障录波器无信号波形,0001 断路器保护动作,0001 断路器保护跳闸失灵开入动作,GY-Ⅰ线主保护1 出现保护跳闸脉冲信号。0001断路器保护沟通三跳动作。
3.1 连接状态搜索矩阵的建立
对案例中各设备信息状态节点进行编号如表4所示。
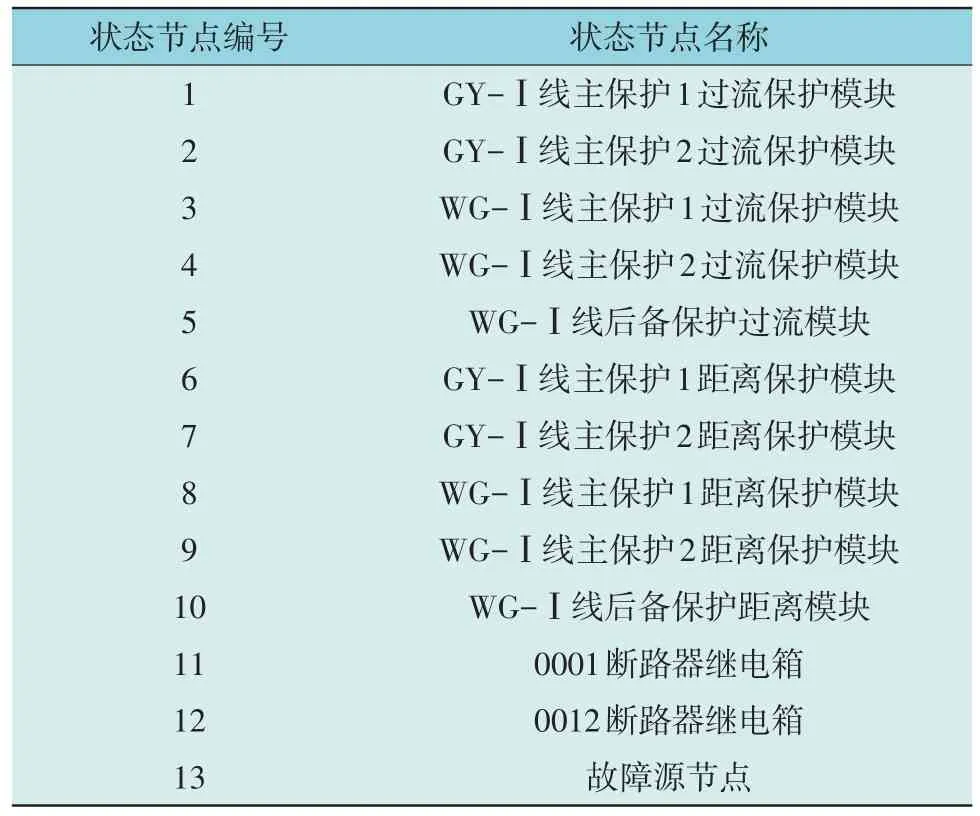
表4 设备节点编号Table 4 Device node numbering
第一次跳闸时,根据现场设备实际情况可进行连接状态矩阵配置,如式(11)所示。
根据第二次送电跳闸过程中对实际设备的分析检查,建立矩阵A′如式(12)。
另外针对神经网络通过故障案例及相关设备运行记录形成训练集及测试集,相关运行记录共5 000条。由于多节点同时故障概率较小,本文中仅考虑单节点故障问题,即limitu=1,计算出的故障状态连接矩阵A*数目最多为2。
3.2 基于模糊RBF神经网络的参数优化
将5 000 条数据按7:3 的比例形成训练集与测试集,对模糊RBF 神经网络进行权重训练。改变模糊化层节点数量进行多次训练,设定迭代结束条件为准确率达0.95 或迭代次数至400。不同学习率及节点数量下的准确率结果如表5 所示。由表5可知,在不同试验条件下,均未达到准确率0.95 的结束条件,当学习率为0.01,模糊化层节点数量为5时准确率最高。
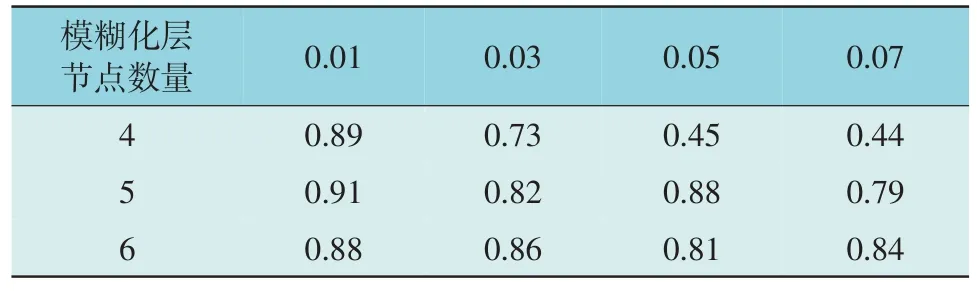
表5 不同学习率及节点数量下的准确率Table 5 Accuracy with different learning rates and thenumber of nodes
另外使用相同的5 000 条数据集,仍按7:3 的比例形成训练集与测试集,在隐藏层节点数为5时,将模糊RBF 神经网络与BP 神经网络、循环神经网络在不同学习率下的准确率进行了对比,结果如表6 所示。
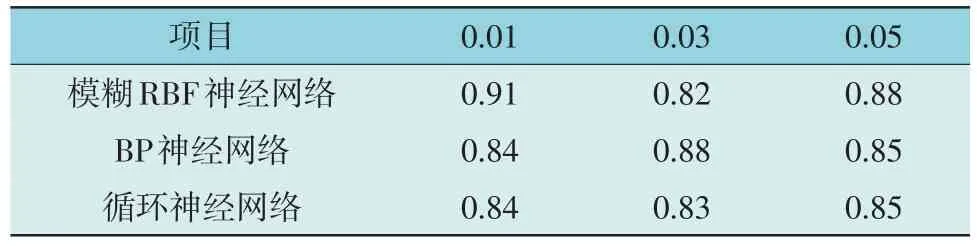
表6 不同学习率下不同神经网络模型的准确率比较Table 6 Comparison of accuracy between different neural network models with different learning rates
由表6 可以看出,在0.01 的学习率下,模糊RBF神经网络的准确率最高,达到了0.91。相比之下,BP 神经网络和循环神经网络在相同学习率下的准确率分别为0.84 和0.84。随着学习率的增加,这些模型的准确率有所变化,但模糊RBF 神经网络在所有测试的学习率下均保持了最高的准确率。这表明,在这些特定的条件下,模糊RBF 神经网络在性能上优于BP 神经网络和循环神经网络。
3.3 故障搜索定位结果分析
第一次跳闸时,二次系统状态向量S为:
根据现场跳闸情况及GY-Ⅰ线主保护1 与WG-Ⅰ线备用保护的监测信号,可得到此时的二次系统状态解析结果为:
根据状态解析结果d,计算得到最终状态Se,如式(15)—式(18)所示,与第1 次跳闸时的连接状态矩阵比较可以发现,异常节点元素为{(})13,10,验证状态与解析结果符合,说明故障矩阵A*符合实际故障情况。
式中:S″为计算状态S′改变后的二次系统后一状态向量。
将异常节点元素坐标进行编码转换输入神经网络,输出结果为二进制10,根据前述的故障类型二进制编码可知,该异常节点元素可反映故障类型1,表示WG-Ⅰ线后备保护距离模块故障。现场检查发现,故障原因为WG-Ⅰ线后备保护直流电源输出电压异常,引起WG-Ⅰ线后备保护输出异常电平,导致扰动出现时继电器异常动作。利用故障搜索方法得到的结果与现场检查结果一致。
第2 次跳闸时,初始状态向量与第1 次跳闸时相同。根据二次跳闸时的现场情况及保护监测信号,得到此时的状态解析结果d′如式(19)。
同理可得故障节点的搜索结果为{(13,6),(13,11)}。输入神经网络可得到输出结果为二进制10,异常节点(13,6)表示GY-Ⅰ线主保护1 距离保护故障,异常节点(13,11)表示0001 断路器继电箱故障。现场检修发现,WG-Ⅰ线主保护1 的供电电源异常,导致WG-Ⅰ线主保护1 输出异常电平,最后导致0001 断路器继电箱输出错误动作信号。故障搜索结果与现场检查情况一致。
4 结论
本文将二次系统设备拓扑连接关系抽象为矩阵描述,表明了智能变电站二次系统设备间的实际连接关系及通信关系等;以各节点的监测状态作为矩阵元素,并在此基础上通过矩阵计算与神经网络方法实现了二次系统的故障搜索定位,得到以下结论:
1)基于连接矩阵关系及神经网络的故障搜索定位方法具有一定通用性。连接矩阵是通过二次系统各设备节点间的物理或虚拟连接关系建立的,能够较好地描述二次系统各设备间的连接状态并及时反映状态变化。对连接矩阵进行动态修正,不受设备连接顺序、设备数量等影响,具有一定的通用性。
2)基于连接矩阵关系及神经网络的故障搜索定位方法具有较高的准确性。故障定位搜索方法中针对二次系统分别独立建立了连接矩阵及状态解析结果,利用状态解析结果对矩阵进行校验,能够充分利用各节点间的耦合信息,在此基础上利用径向基神经网络得到准确率较高的故障类型结果,具有较高的准确性。
