基于改进概率神经网络的储能电池荷电状态估计
2024-02-27翟苏巍李文云侯世玺
翟苏巍,李文云,周 成,汪 成,侯世玺
(1.中国南方电网云南电网有限责任公司电力科学研究院,云南昆明 650217;2.中国南方电网云南电力调度控制中心,云南昆明 650011;3.河海大学人工智能与自动化学院,江苏南京 210098)
0 引言
随着双碳战略的推进,清洁能源在能源结构中的比重越来越高,储能系统作为清洁能源的重要支撑将迎来蓬勃发展。作为储能系统的重要组件,锂离子电池的运行状态逐渐受到研究人员的重视[1-5]。荷电状态(State of Charge,SOC)是锂离子电池重要的状态信息,通常被定义为电池剩余电量与最大电量之比,用来为电池管理系统充放电策略提供参考,防止过充或过放。SOC 不可直接测量,只能通过测量电压、电流等进行间接估算[6-10]。
目前,学者们提出了多种锂离子电池SOC 估计方法,可以概括为两类:物理模型估计方法和数据驱动估计方法[11-13]。物理模型估计方法主要包括安时积分法和开路电压法[12-13]。安时积分法计算简单,只需将锂离子电池充放电过程中的电流随时间积分,进而计算锂离子电池的荷电状态。然而,该方法的累计误差随时间延长而增加,因此需要定期校准。开路电压法具有较好的估算精度,但需要长时间将电池静置,不适用于实时SOC 估计。数据驱动估计方法主要包括卡尔曼滤波和神经网络(Neural Network,NN)[14-17]。卡尔曼滤波具有良好的稳定性和适应性,但其估计精度高度依赖电池模型的准确性。NN 具有强大的拟合能力,受到众多研究人员的青睐。
NN 法无需构建精确电池模型,已被广泛应用于电池状态估计[18-24]。使用神经网络估计电池状态是一个非线性映射问题,选择适当的神经网络结构非常必要。传统BP 神经网络对权重变化敏感,容易陷入局部最优解,概率神经网络(Probabilistic Neural Network,PNN)可以很好地克服BP 神经网络的缺点,实现全局最优[25-26]。文献[21]中,PNN 被应用于锂离子电池充电,可以在负载变化时改善电压调节的瞬态特性,使锂离子电池充电更安全、更高效。然而PNN 也存在固有的缺陷,即推理机制相对固定。为了解决这个问题,补偿神经网络通过补偿学习算法为神经网络提供额外的自由度,从而优化推理机制[27-28]。
为了更好地实现SOC 估计,本文提出一种融合补偿机制的改进概率神经网络(Modified Probabilistic Neural Network,MPNN)。MPNN 创新性地结合了概率层和补偿机制,同时通过阈值层加强了对数据特征的学习和处理能力,显著提升了SOC 估计的准确性。最后通过公开数据集实验测试验证了MPNN在实际应用中的有效性。
1 SOC估计基础
常见的锂离子电池等效电路图如图1 所示,其中V0表示端电压,V1表示开路电压,V2表示极化电压,R1表示等效电阻,R2表示扩散电阻,C表示电容,I表示回路电流,Δd表示总扰动。
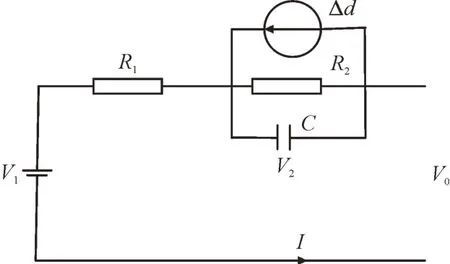
图1 锂离子电池等效电路图Fig.1 Equivalent circuit diagram of Li-ion batteries
锂离子电池的SOC 是指电池的剩余电量,可表示为SLiB。其计算方法如下:
式中:Qc为当前电量;Qmax为最大电量。
然而,通过图1 中的等效模型估算SOC 较为复杂,往往需要建立多个微分方程并考虑未知扰动[29]。从数学角度来看,SOC 与电压、电流等可测量物理量是非线性函数关系。为了准确获取可测量物理量与SOC 之间的非线性映射关系,同时避免建立复杂物理模型,本文通过改进概率神经网络以数据驱动的形式实现SOC 估计。
2 MPNN结构
本文所设计的MPNN 如图2 所示。MPNN 共有8 层网络结构。
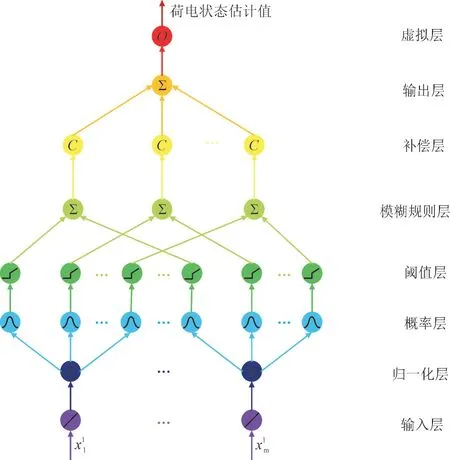
图2 MPNN结构Fig.2 Structure of MPNN
2.1 输入层
输入层有m个网络节点,用于传输m个可测量物理量。具体的输入输出定义如下:
2.2 归一化层
为了消除单一样本数据带来的不利影响,提高网络的学习速度,引入归一化层。其计算方法如下:
2.3 概率层
概率层采用高斯径向基函数,根据实际问题设置n个分类节点,每个节点的输入和输出分别由式(6)和式(7)给出。引入概率层的目的是为了便于训练,避免BP 神经网络的局部最优问题。
需要指出的是,通过式(7)计算出的输入概率信息会传递给后续层。
2.4 阈值层
阈值层中的节点与概率层中的节点一一对应。通过设置阈值,可以保留相对重要的概率信息,减少次要信息的影响。设计思路如下:
2.5 模糊规则层
在模糊规则层中,为了理解不同输入对最终输出的影响,制定1 条模糊规则:将1 组阈值层输出的加权总和作为模糊规则层1 个节点的输出。
2.6 补偿层
补偿层在网络中引入1 组自由变量,然后优化模糊推理机制,网络性能优于普通模糊神经网络(Fuzzy Neural Network,FNN)。模糊补偿策略由式(14)给出,各节点设计如下:
2.7 输出层
输出层只有1 个节点,即SOC 估计结果f7,由式(17)得到。
值得注意的是,为了加快MPNN 的学习收敛速度,对学习样本的输入和输出都进行了归一化操作。因此,此时的SOC 估计结果是归一化的结果,需要在下一层进行反归一化。
2.8 虚拟层
MPNN 的核心结构是前7 层,虚拟层的存在意义是用于数据处理得到SOC 的估计值。计算公式如下:
式中:x8为虚拟层的输入;Qmin为学习样本的最小锂离子电池电量。
3 基于MPNN的SOC估计
在实际的锂离子电池应用中,往往很难建立准确的电池模型。MPNN 通过大量的数据学习,建立可测数据特征与SOC 的非线性映射模型,恰好克服了电池模型难以建立的缺点。具体训练过程可归纳如下:
式中:pre为训练指标,本文采用绝对误差和(Sum of Absolute Errors,SAE);N为训练样本数;为样本i的参考输出值;为样本i的估计输出值,为参考输出值与估计输出值的差值。
2)进行SOC 估计。样本i的SOC 将通过MPNN进行估计。
3)参数调整。损失函数E定义为式(21),参数通过梯度下降法调整。
图3 为基于MPNN 的SOC 估计流程图。由图3 可以看出,通过采集电池充放电测试时电压、电流和温度等数据,划分训练数据集和测试数据集,根据这些数据和选定的评价指标训练MPNN。训练完成后,将采集的电池实时运行数据输入到MPNN中,即可得到SOC 的估计输出。

图3 基于MPNN的SOC估计流程图Fig.3 Flow chart of SOC estimation based on MPNN
MPNN 的初始参数设计非常重要,本文选择的初始参数如下:概率层中每个节点的中心是从0到1 的n截面点,对应的宽度为1/n,且n=100;阈值设计为th=0.001;cij设计为0.5;都是0 到1 之间的随机数。用于网络调整的参数和的值均取0.01。值得注意的是,这些参数都是通过反复试验得到的,不合理的参数设计会导致网络学习失败。一般来说,概率层的中心应覆盖整个输入空间,相应的宽度不应超过相邻中心之间距离的一半。补偿程度由输入变量的个数m决定,设计为0.5m。
4 仿真结果
为验证MPNN 在SOC 估算中的可行性,选取18650-20R 锂离子电池作为测试算例,其具体参数如表1 所示。本节进行两项测试,即小电流测试和动态电流测试。值得注意的是,学习数据和测试数据均来自CALCE Battery Research Group 公开的电池数据,是在温度恒定的情况下获得的。本文以电池电压、电流、温度为输入变量,SOC 为输出变量构建数据集。为了综合评估MPNN 在SOC 估算中的效果,引入平均绝对误差(Mean Absolute Error,MAE)(量值为EMA)和均方根误差(Root Mean Square Error,RMSE)(量值为ERMS)作为参考指标。

表1 18650-20R的参数Table 1 Parameters of 18650-20R
4.1 小电流测试
小电流测试包括充电和放电过程。充电过程中,将完全放电的电池以0.1 A 的恒定电流充电,观察并记录SLiB值从0 变化到0.8 的数据。图4 和图5 分别给出了SLiB值估计结果以及小电流充电过程中SLiB值估计相对误差,其中红色实线代表真实SLiB值,黑色虚线代表运用MPNN 估计的SLiB值。由图4、图5 可以看出估计结果较好,相对误差稳定在1%以内。

图4 小电流充电期间SLiB估计Fig.4 SLiB estimation during low current charging
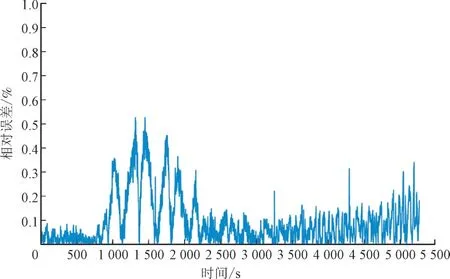
图5 小电流充电期间相对误差Fig.5 Relative error during low current charging
同样以0.1 A 的恒定电流进行放电测试,观察并记录SLiB值从0.8 到0.1 的数据。图6 和图7 分别给出了SLiB值估计结果以及小电流放电过程中SLiB值估计相对误差。由图6、图7 可以看出估计结果较好,相对误差稳定在1%以内。
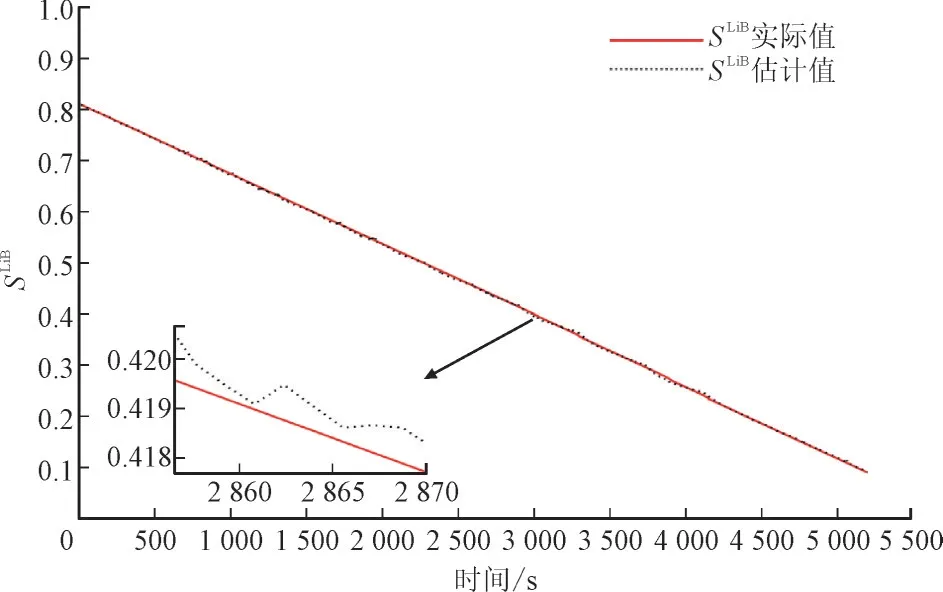
图6 小电流放电期间SLiB 估计Fig.6 SLiB estimation during low current discharging
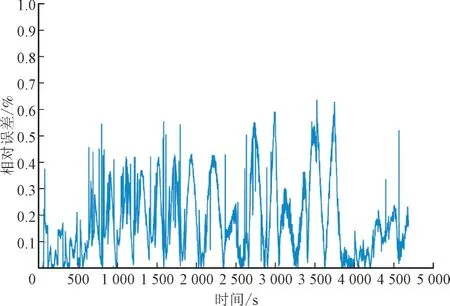
图7 小电流放电期间相对误差Fig.7 Relative error during low current discharging
4.2 动态电流测试
虽然MPNN 在恒定小电流充放电过程中可以很好的进行SLiB值估计,但是在实际电池充放电过程中电流并不是恒定的。为此,本节进行了动态电流测试,以观察和记录MPNN 在动态电流下估计SLiB值的能力。
图8 给出了FNN,PNN 和MPNN 的SLiB值估计结果。从图8 中可以看出,这3 种方法都可以较好地估算锂离子电池的SLiB值。图9 给出了FNN,PNN 和MPNN 的相对估计误差。从图9 中可以看出,FNN 的估计误差较高,PNN 的估计误差仅能做到小于3%,而MPNN 的估计误差小于1%,这是因为通过优化推理机制,模型精度提高。

图8 动态电流期SLiB 估计Fig.8 SLiB estimation during dynamic current
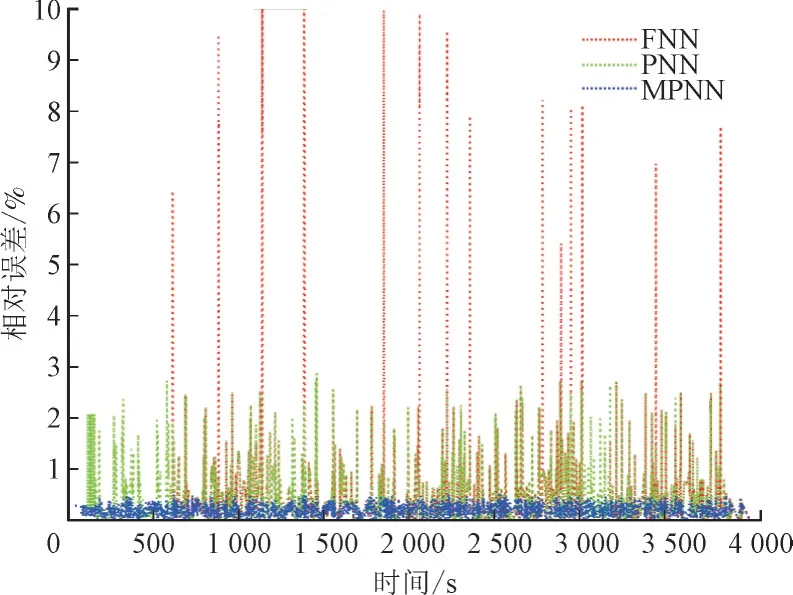
图9 动态电流期间相对误差Fig.9 Relative error during dynamic current
为进一步分析算法性能,增加了不同温度下动态电流测试实验,3 种方法的EMA和ERMS如表2 和表3 所示。从表2 和表3 可以看出,不同温度下使用MPNN 方法的EMA和ERMS比PNN 和FNN 方法均有明显降低,说明MPNN 的SLiB值估计准确性在不同温度下均优于PNN 和FNN。这些结果证明了MPNN 在SLiB值估计方面的准确性及其适用性。通过更精确的估计,有助于提高整个储能系统的性能和可靠性。
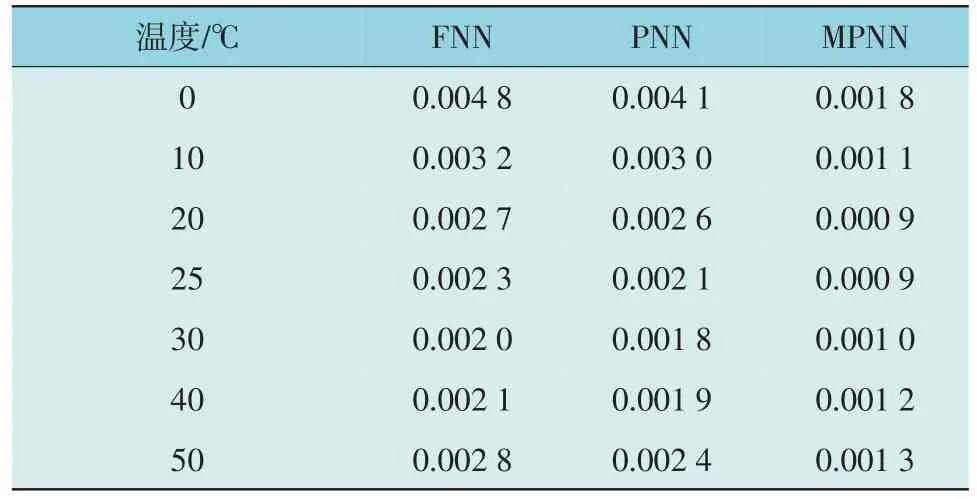
表2 不同温度下3种方法EMA 统计Table 2 EMA obtained by three methods under different temperatures
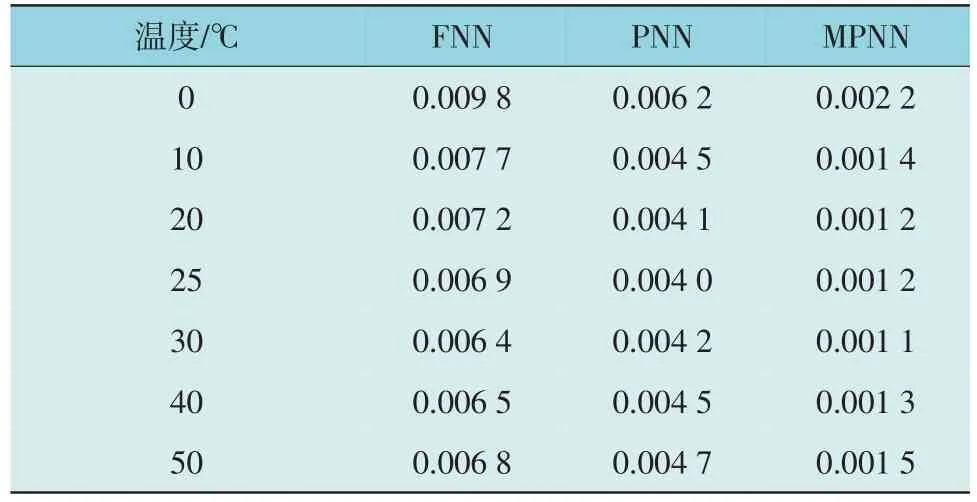
表3 不同温度下3种方法ERMS 统计Table 3 ERMS obtained by three methods under different temperatures
5 结语
本文提出了1 种改进概率神经网络估计锂离子电池的荷电状态。MPNN 本质上是1 种数据驱动的方法,通过引入概率函数,避免BP 神经网络的局部最优问题,加快收敛速度。此外,MPNN 通过引入补偿机制,优化了推理机制,弥补了传统神经网络的不足,提高了学习成功率。最后,将MPNN 用于估计18650-20R 锂离子电池的荷电状态,测试结果表明,在小电流和动态电流下SLiB值估计效果均达到预期。
