面向高维不平衡医学数据的特征选择算法
2024-02-27王远军
苏 璇,王远军
(上海理工大学 医学影像工程研究所,上海 200093)
0 引 言
随着现代科技的飞速发展,大量数据随之产生,这些数据往往具有高维、类别不平衡、重叠、缺失等问题.医学数据是现实世界中最重要的数据,也是最常见的极端数据.面对这些极端数据,现有特征选择算法仍无法获得良好的特征子集来提高机器学习算法的预测或分类精度[1],故提出高效的特征选择算法尤为关键.特征选择其本质是优化问题,按照所涉及的学习算法级别可分为过滤型(Filter),封装型(Wrapper),嵌入型(Embedded)[2],如表1所示.此外,随着数据维度的增加,有研究将多种类型特征选择算法融合,构建多级特征选择算法[3,4].尽管多级特征选择可以在一定程度上有效降低数据维度,但高维不平衡数据仍然给这些特征选择算法带来巨大挑战.

表1 传统医学数据特征选择算法Table 1 Traditional feature selection algorithms on medical data
目前处理高维不平衡数据问题,主要从数据处理层面和算法层面出发[5].在数据处理层面常用SMOTE(Synthetic Minority Oversampling Technique)[6]过采样、欠采样等算法以及改进算法,如K-means SMOTE算法[7]等.这些算法用来改变原始数据分布,进而改善学习算法分类结果.算法层面可以细分为单类学习算法[8,9]、特征选择算法[10-19]、成本敏感机器学习算法[20-23]、集成学习算法[24,25],后两者容易受到噪声和高维数据的影响.特征选择算法中文献[10-13]仅考虑了高维和不平衡问题其中的一个,但是有研究同时考虑高维不平衡数据的交叉问题,甚至考虑二者对分类精度的交互影响[14-19].如文献[15]提出了一种基于条件特征与K个最近邻决策类之间的依赖关系的在线特征选择算法,用于选择高维特征,称为K-OFSD,研究中还提炼了邻域粗糙集理论来改善选择的不平衡数据集特征.
近年来,元启发式算法被广泛应用于极端数据集处理.如竞争群优化器CSO(Competitive Swarm Optimizer)[12],遗传算法GA(Genetic Algorithm)[26],粒子群算法PSO[27],海洋捕食者算法(Marine Predators Algorithm MPA)[28]等.海洋捕食者算法是Faramarzi等人[29]在2020年提出的元启发式算法,灵感来源于海洋生物的莱维Lévy和布朗Brownian觅食策略以及捕食者和猎物之间的相互作用.该算法已经应用于COVID-19检测和图像分割[30,31]、预测[32]、多目标优化[33]、特征选择[2,28,34,35]、参数优化等领域.此外,在MPA算法改进方面取得了以下进展:
①为了强化初始化种群的多样性来扩大搜索范围,从而提高算法的收敛速度和精确度,随机对立[28]、Tent混沌对立[36]、逻辑对立[37]、准对立学习策略[38]和Cubic混沌映射[39]的方法被用来初始化种群.
②为了强化MPA算法搜索空间的能力,有研究将局部搜索能力较强的算法和MPA算法结合,如引入差分进化算法的ODMPA[38]、引入樽海鞘群算法的MPASSA[40]、引入正弦余弦SCA算法的MPASCA[41]、引入粒子群优化的MPA算法IMPAPSO和引入飞蛾火焰优化MFO算法的MPAMFO[42].
③为了优化迭代次数不足导致的过早收敛问题,文献[34]将分数阶微积分的综合学习策略原理和记忆视角纳入MPA,文献[43]提出了一种基于综合学习和动态多群方法的MPA变体,文献[44]提出了基于分布和粒子群优化的MPA变体,文献[45]研究MPA的不同控制参数对实验的影响.
④为了优化迭代后期种群多样性降低的问题,文献[39]使用混合估计分布算法对优势种群信息进行采样并修正进化方向,此外还采用高斯游走策略在算法停滞时帮助算法跳出局部最优.
⑤优化MPA原始参数[37,46]CF以及引入非线性控制参数来实现全局最优化并平衡算法开发和探索能力.
尽管上述算法对原始MPA做了很多改进,并将其应用到了特征选择领域,但是还未提出针对高维不平衡数据集的MPA改进算法.就MPA算法本身而言,在改善迭代后期种群多样性、计算成本、过早收敛和重复搜索等方面还有极大的改进空间.本文的主要贡献如下:
a.引入不平衡数据集的评估标准G-mean代替全局分类准确度来改进适应度函数,以选择有利于少数类识别的特征.
b.改进CF参数来提高全局收敛性,引入基于动态边界的精英反向学习来强化迭代期种群多样性.
c.分析适应特征选择算法的迭代次数分布,第2阶段的人口分布以及FADs值.
d.分析算法的收敛性,复杂度,并将所提出的算法GEMPA在基准函数上进行测试并与现有算法对比分析.
1 相关工作
海洋捕食者算法MPA[29]算法遵循莱维Lévy和Brownian布朗运动的觅食策略以及捕食者和猎物之间相互作用的最佳遭遇率策略.其Lévy和Brownian运动的数学模型如下所示:
(1)
布朗运动是随机的,可从高斯分布的概率函数中获得步长,其均值μ为零、单位方差σ为1.
(2)
(3)
(4)
Lévy[2]是一种随机游走,文中使用Magneta方法生成基于Lévy分布的随机数.其中x和y是两个正态分布变量.MPA算法基于上下限Xmin、Xmax以及[0,1]均匀随机向量进行随机初始化,如式(5)所示:
X0=Xmin+rand(Xmax-Xmin)
(5)
搜索过程中最具觅食天赋的顶级捕食者被用来构建精英矩阵Elite,该矩阵会根据猎物矩阵Prey更新.式(6)中第1行表示顶级捕食者向量,将其复制n次以构建Elite矩阵.n是搜索代理的数量,而d是维度的数量.
(6)
另一个与Elite维度相同的矩阵称为Prey,如式(7)所示:
(7)

(8)
(9)

(10)
后半部分个体数学模型如式(11)所示,其中CF被视为控制捕食者运动步长的自适应参数.
(11)
(12)
(13)
第3阶段处在高开发阶段,捕食者速度远大于猎物,且此时的最佳策略为Lévy运动,数学公式如下:
(14)
优化阶段外,现实情况中的涡流或鱼类聚集FADs效应会导致局部最优停滞.因此,为避免局部停滞在模拟过程中FADs效应在数学上表示为:
(15)
2 改进的捕食者特征选择算法
2.1 基于不平衡数据的目标函数
(16)
为了更好的评价不平衡数据分类性能,Kubat等人[48]提出度量两类样本精确度的几何平均值G-means,其数学定义为:
(17)
(18)
式中TP为真阳率,FP为假阳率,FN为假阴率,TN为真阴率.Sensitivity灵敏度衡量的是所有阳性样本中被正确分类的数量,Specificity特异度衡量的是所有阴性样本中被正确分类的数量.将二者几何均值G-means引入优化算法的目标函数,可以改善不平衡数据的特征选择问题,定义见式(19),其中a,b分别取0.99和0.01.
(19)
2.2 精英反向学习

(20)
2.3 参数改进
针对MPA算法参数改进主要分为两个方面:1)提出新的CF参数记为CFnew,如图1所示.CFnew不仅加快了前,中期搜索进展,而且在搜索后期同CF可以确保算法精细化寻找最优解;2)对迭代次数分布Iter、第2阶段个体分布、FADs进行实验,选出最适配的分布组合.CFnew参数的定义如式(21)所示:
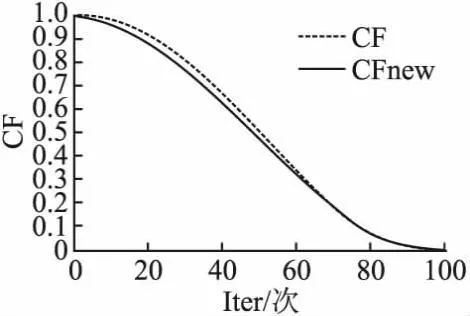
图1 CF参数改进Fig.1 Improvement of CF parameters
(21)
2.4 复杂度分析
针对本文改进的MPA特征选择算法的时间复杂度和空间复杂度问题,本文使用O(N×d)表示需要建立参数并初始化随机群体的时间复杂度,其中N是总体数,d是搜索维数.该算法包含基于不同速度比和捕食者和猎物运动的3种情况,这部分需要O(N×d)的时间复杂度.外循环需要O(T)的时间复杂度,其中T是最大迭代的总数.此外,群体位置更新以及精英反向解生成的时间复杂度为O(N),最适解的时间复杂度是O(1),所以,整个算法的时间复杂度是O(T×N×d).为了计算所提出系统的空间复杂度,使用精英矩阵、精英反向矩阵和位置矩阵,3个矩阵都使用N个总体和d个维度,因此算法总的空间复杂度为O(N×d).综上所述,本文提出了基于改进的MPA高维不平衡数据特征选择算法,称为基于G-means的精英反向解MPA算法(Elite Opposition Solution MPA Algorithm Based on G-means,GEMPA),其具体实现流程如图2所示,具体实现伪代码如图3所示.

图2 GEMPA算法流程Fig.2 Flow of the GEMPA algorithm

图3 GEMPA算法伪代码Fig.3 Pseudocode of GEMPA algorithm
算法:GEMPA
输入:搜索代理个体数N,最大迭代次数Max_Iter,数据集D
嗯。当时,根本没细想,闭着眼睛只管朝他身上捅。怕他不死。要不是旁边有小孩吓得哭起来,可能还不止十四刀。
输出:F-measure值,选择的特征数,迭代时间,收敛曲线
初始化随机个体Xi(i=1,2,…,N)(公式(5))
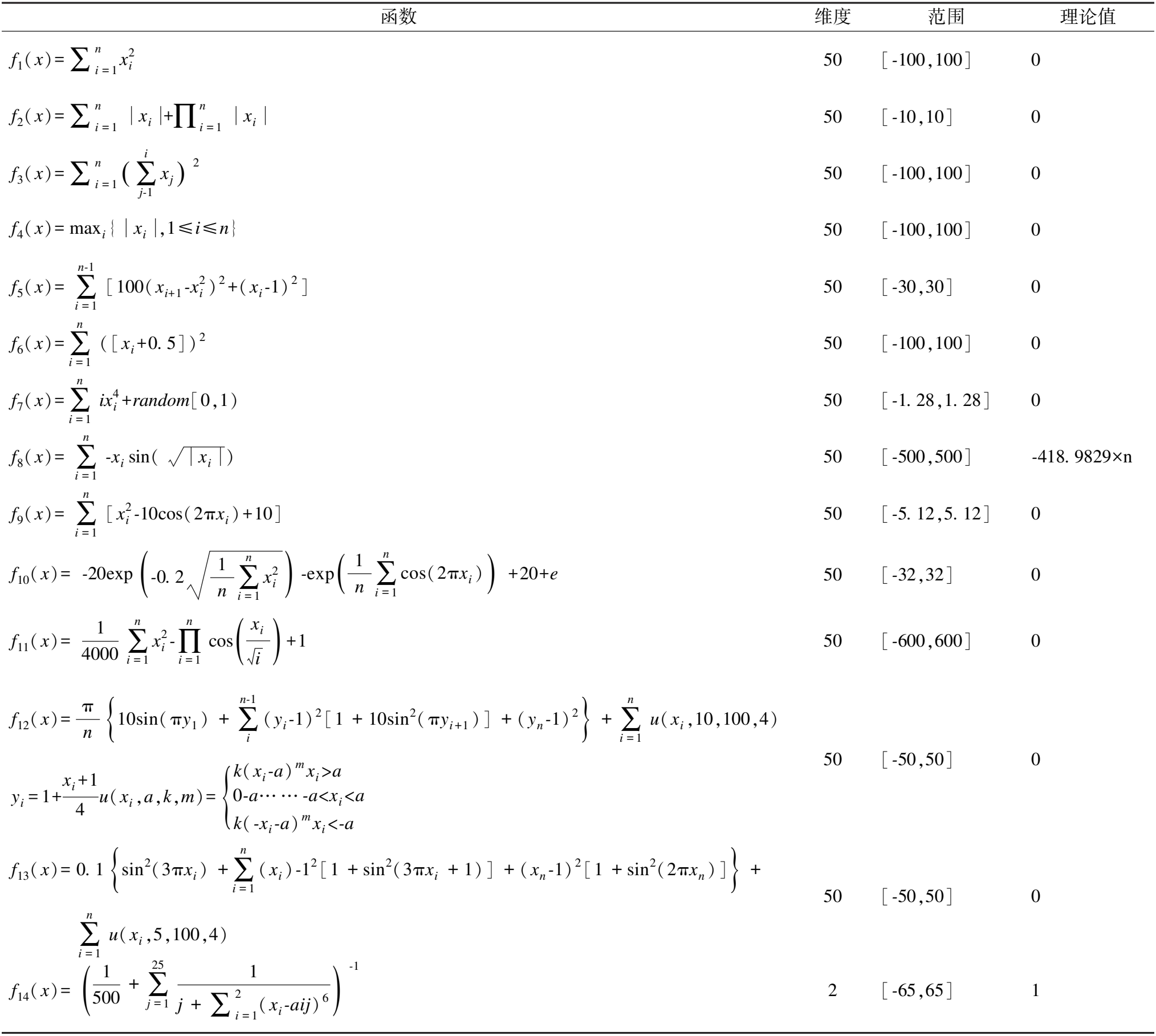
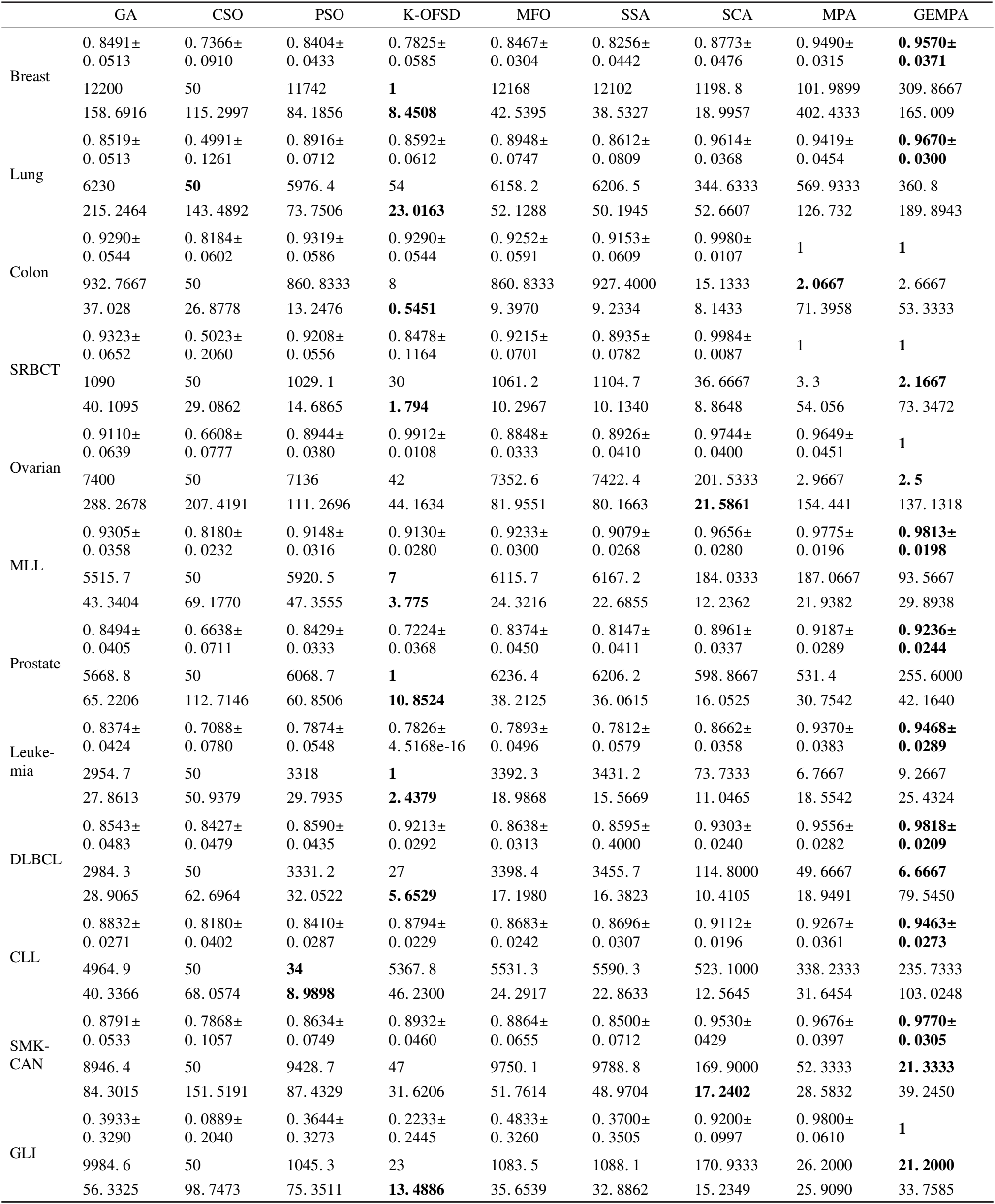
while Iter 基于成本函数计算最新的适应度(公式(19)) 调用KNN作为分类器,G-means作为评估指法标的成本函数建立精英矩阵Elite(公式(6)),并生成自适应参数CF(公式(21)) 本文采用的实验环境为Windows10,64位操作系统,CPU为AMD Ryzen 7 4800H,主频为2.90GHz,内存为8.00GB.本文采用的编程环境为Matlab2016b. 为了测试GEMPA算法以及每个优化方法的有效性,本文采用14个测试函数,具体信息如表2所示.本文将初始参数设置为最大迭代次数500,搜索个体25,P为0.5,FADs为0.2,接着对14个测试函数分别进行了5个算法的对比,分别为原始MPA函数、改进参数的MPA1(迭代次数:3/5,1/5,1/5,开发和勘探个体:1/3,2/3)、引入CFnew的MPA2、引入基于动态边界精英反向矩阵的MPA3和GEMPA,测试结果如表3所示.从表3可以看出,14个测试函数中10个函数,GEMPA以及每个优化方式都优于MPA算法的最优收敛解.其中f9,f11已经获得最优解.只有f5,f6,f12,f13的最优解差于MPA算法,主要因素在于MPA1参数分布让算法偏离了最优解,同时这也说明分析MPA算法个性化的参数分布方案是有必要的. 表2 测试函数Table 2 Test function 表3 优化算子对比分析Table 3 Comparative analysis of optimization operators 为了评估GEMPA特征选择算法性能,收集来自公开UCI机器学习数据库https://archive.ics.uci.edu/ml/index.php的Breast、Lung数据集,链接https://leo.ugr.es/elvira/DBCRepository/的Prostate和DLBCL数据集,链接https://jundongl.github.io/scikit-feature/OLD/datasets_old.html的CLL-SUB-180(CLL)、GLI-85(GLI)和SMK-CAN-187(SMK-CNA)以及文献[45]涉及的Colon、Ovarian、MLL、SRBCT、ALL-AML(Leukemia)数据,见表4. 表4 数据集相关介绍Table 4 Introduction of datasets 为了避免不平衡数据在分类过程中趋向全局准确率最高而忽略少数样本分类情况的问题,针对不平衡数据集有专门的评估指标F-measure.F-measure是召回率Recall和精确度Precision的调和平均值,定义如下: (22) 为了衡量算法选择的特征数量以及计算代价,本文引入特征数量和时间两个评估指标,为了确保算法的鲁棒性,本文多次重复实验并取均值和标准差,定义如式(23)所示.其中,K为总重复次数,k为第k次实验,time为单次运行时间,subset为单次选取的特征子集数量. (23) 考虑到MPA算法原本参数对特征选择的影响,本文选取高维不平衡数据集Lung作为基准数据集,分别对MPA算法的迭代次数分布、第2阶段开发和勘探个体分布和FADs进行对比分析.首先分配10种迭代次数分布方案,固定单次最大迭代次数为100,重复10次,FADs为0.2,开发和勘探个体各为一半. 由表5可知,当迭代次数分布为3/5,1/5,1/5时GEMPA算法取得最优的分类精度,因此,本文固定当前的分布进而改进开发和勘探的个体分布,实验结果如表6所示.结果显示在分布为1/3,2/3时精度最高,接下来将其固定,对实验进行FADs参数分析,结果显示FADs为0.2时精度最高.以同样的方式,本文也依次对精英反向矩阵的引入和CFnew进行了测试,对应的精度、特征数量、时间的结果分别为:0.9766±0.0322,453,194.0186;0.9815±0.0217,264.3000,181.0215.可以看出改进后精度得到了提升,而且特征数量减少了约50%,运行时间的变化也在可接受的范围内,说明对于高维不平衡数据而言,本文的改进起到了很好的效果. 表5 迭代次数分布分析Table 5 Analysis of the number of iterations distribution 表6 开发和勘探个体分布分析Table 6 Analysis of the distribution of exploration and exploitation 本文选取针对高维数据的竞争群优化器CSO算法[12],针对高维不平衡数据的在线特征选择算法K-OFSD[15],常见的元启发式特征选择遗传算法GA[26],粒子群算法(Particle Swarm Optimization,PSO)[27],MPA算法[28],樽海鞘算法(Salp Swarm Algorithm,SSA)[40],正弦余弦算法(Sine Cosine Algorithm,SCA)[41],飞蛾扑火优化(Moth-Flame Optimization,MFO)[42]与新提出的GEMPA对比分析,分析时每个算法重复运行30次,每次迭代100次,如表7所示.表7中每个数据集对应3行从上到下依次为F-measure均值Ave-F以及标准差,特征数均值Ave-num,运行时间均值Ave-time.从表7中可见新提出的特征选择GEMPA算法在12个数据集上表现优异,在Colon和SRBCT两个数据集上同MPA实现了100%分类精度,在其余10个数据集上实现了最高的分类精度.GEMPA在12个数据集上特征选择的比例分别为Breast:1.27%,Lung:2.87%,Colon:0.13%,SRBCT:0.09%,Ovarian:0.02%,MLL:0.74%,Prostate:2.03%,Leukemia:0.13%,DLBCL:0.09%,CLL:2.08%,SMK-CAN:0.11%,GLI:0.10%,这说明GEMPA算法有能力高效地自适应剔除非必要特征.在SRBCT,Ovarian,DLBCL,SMK-CAN,GLI 5个数据集上不仅精度最高还保留了最少的特征数.针对30次重复运行的平均时间来看,GEMPA算法时间维持在400秒以内,相对其他算法而言运行时间相对较长,但是根据4.7的分析,GEMPA在部分数据集上收敛迭代次数较少,可以节省时间. 表7 特征选择算法对比分析Table 7 Comparative analysis of feature selection algorithms 本文引入Friedman[50]非参数检验来分析GEMPA,GA,K-OFSD,CSO,MPA,SSA,SCA,MFO,PSO共9种算法呈现出的显著性(P=0.000<0.01),这意味着9种算法之间呈现统计意义上的显著差异,差异情况具体见图4.此外,9种算法分别对应的秩均值为8.92,4.88,3.88,1.00,7.83,3.00,7.08,4.50,3.92.秩均值越高的算法效果越好,因此,秩均值为8.92的GEMPA算法性能优于其他8种算法. 图4 算法差异箱线图Fig.4 Boxplot of algorithmic differences 9种算法中K-OFSD不涉及收敛问题,为了直观展现其余8个算法在12个数据集上的收敛性本文引入平均收敛曲线,如图5所示,其中x轴代表的是迭代次数,y轴代表的是目标函数的适应度值,曲线无限逼近x轴的过程就是收敛过程.收敛曲线以图形形式描述适应度函数与迭代次数之间的关系,进而通过各个算法之间的比较揭示性能最佳的算法.从图5中可以看出GEMPA算法在12个数据集上都能快速的收敛到最优的适应度值,曲线光滑,没有长时间陷入局部最优值,在数据集Breast,SRBCT,Ovarian,Colon和GLI上执行50次迭代就已经收敛,在3个数据集上100次迭代收敛,在4个数据集上收敛的迭代次数大于100次,且在7个数据集上达到了最佳收敛.MFO、SCA、GA和CSO这4种算法在大部分数据上收敛的迭代次数大于100.可见GEMPA算法具有良好的收敛性. 图5 算法收敛性分析Fig.5 Convergence analysis of algorithms 本文针对高维的不平衡数据集对MPA算法进行改进,在原始算法的基础上考虑改进算法迭代期个体多样性,改善CF参数加快MPA算法的收敛,分析适合特征选择的参数方案,并通过G-means构建针对高维不平衡数据的优化目标函数.通过实验结果分析可知,GEMPA算法相对于现有算法选择的特征可以在一定程度上提高高维不平衡数据集的分类性能,特别是少数样本的分类性能,有效解决了因多数类样本精确度高而导致的整体准确率高的问题.因此,GEMPA算法可以应用于传统机器学习分类和预测问题的特征选择部分,他不仅可以应用于高维不平衡数据特征选择,还可以应用于平衡数据集.特征选择的数据集也不局限于医学数据. GEMPA存在一定的局限性,GEMPA算法是先选取特征子集,再将子集的每个个体依次带入KNN分类器进而计算适应度值,这就加大了该算法的运行时间,因此寻找更高效的特征子集适应度计算方案是下一步的研究重点.3 实验分析
3.1 基准函数测试

3.2 实验数据

3.3 评估指标
3.4 参数分析


3.5 特征选择算法对比分析
3.6 统计分析

3.7 收敛性分析

4 结 论
