基于多任务学习的轨道交通短时客流预测研究

张含笑 刘宇然 刘媛 牛子辰

摘要：为了精准预测轨道交通的短时客流量，有效缓解城市交通拥堵，提出了一种基于多任务学习的轨道交通短时客流预测模型，该模型采用残差卷积神经网络和嵌套式长短期记忆神经网络提取客流的时空相关性，引入注意力机制加强模块对特征的提取效果。考虑轨道交通运营的特点，模型进一步选取列车运行特征、轨道交通站点周边公交站点以及兴趣点数据作为外部特征，以提高轨道交通短时客流预测精度。基于北京地铁历史客流数据，在10、30、60 min等多时间粒度场景下进行实验。结果显示，该方法通过多任务学习的方式建模分析站点进出站客流之间的相互影响，提高了模型的预测性能和泛化能力，为城市轨道交通短时客流预测问题提供了新的思路。

关键词：轨道交通；客流预测；多任务学习；注意力机制; 深度神经网络

中图分类号：U239.5   文献标志码：A   文章编号：1002-4026（2024）01-0095-12

A multitask learning model for the prediction of short-term subway passenger flow

Abstract∶An accurate prediction of short-term subway passenger flowscan effectively alleviate traffic congestion and improve the quality of travel services for urban residents. Herein， we propose a multitask learning-based model for the prediction of short-term subway passenger flows， which uses a residual convolutional neural network （NN） and a nested long short-term memory NN to extract the spatio-temporal correlation of traffic patterns， and introduces an attention mechanism to enhance the feature extraction performance of the NNs. Considering the characteristics of subway operations， the model selects train operation features， bus stops around subway stations， and point of interest data as external features to improve the accuracy of the prediction. Based on the historical data of the Beijing Subway， experiments were conducted in multiple time granularity scenarios， such as 10， 30， and 60 min. The results showed that the methodsuccessfully modeled and analyzed the inflow-outflow interaction through multitask learning， improved the prediction performance and generalization ability of the model， and providednovel approaches for the prediction of short-term subway passenger flows.

Key words∶subway; passenger flow prediction; multitask learning; attention mechanism; deep neural network

城市軌道交通充分利用了地下和地上空间的开发，缓解了城市地面交通压力，提高了市民的出行效率。截至2021年年底，中国大陆地区共有50个城市开通城市轨道交通运营线路283条，运营线路总长度9 206.8 km，全年累计完成客运量236.9亿人次，占公共交通客运总量的分担比率为43.40%[1]。短时客流量是轨道交通运营单位开展运力配置、列车运营计划编制和站点工作人员配备的基础。因此对客流量进行准确和实时的预测，在轨道交通运营部门制定合理的列车行车计划、保障市民的出行需求方面起着至关重要的作用[2]。

城市轨道交通系统具有独特的运行特性，与道路公共交通不同，轨道交通运营遵循更精确的时间表，该特征需要融入到客流预测中[3]。乘客为了节约时间成本，会更倾向于在列车快要到站时进站到达站台等待上车，此时进站客流会出现一定的小高峰。同时，运营商为了运力运量的良好匹配，在编制列车行车计划时便会充分考虑该时段客流量的大小。在出行方面，考虑到轨道交通更多的在人们通勤出行中扮演与公交车进行接驳出行的角色，轨道交通站点周边公交站点的数量和分布特征，对于轨道交通短时客流预测有重要影响。一般情况下，周边公交站点数目越多，该轨道交通站点客流量也会越大。轨道交通站点的客流情况与该站点周边的设施息息相关，兴趣点（point of interest，POI）数据可以表征轨道交通站点周边的土地使用情况与城市功能区分布。例如，周边住宅小区以及企业公司较多的站点，其客流通常会以通勤客流为主。此外，乘客在工作日与非工作日的出行特征也会有所不同。因此，在对轨道交通短时客流预测进行研究时，需要考虑这些外部变量对模型预测精度的影响。随着移动互联网技术、信息通信技术及云计算等技术快速发展，城市轨道交通系统每天都会产生包含交易信息在内的大规模高质量的轨迹数据[4-5]。海量、多源、异构的交通大数据及个性化、多样化的出行需求，对现有基于抽样数据的客流预测方法提出了挑战[6]。近年来，随着计算力和数据量的大幅提升，智能预测技术得到了进一步发展，深度学习成为智能交通系统中诸多问题的解决方案。深度学习方法由多个神经网络层组成，这些神经网络层通过模拟人脑的学习行为，实现对复杂特征的学习过程[7-10]。

对于轨道交通的短时客流量预测，当前研究的方法主要分为3类：传统的基于数理统计的模型、基于机器学习的模型以及基于深度学习的模型。传统的基于数理统计的模型，通过研究历史出行需求遵循的统计规律，来预测未来短时的出行需求，例如，移动平均模型（moving average， MA）、自回归移动平均模型（autoregression and moving average model ，ARMA）、自回归差分移动平均模型（autoregressive integrated moving average model，ARIMA）、逻辑回归等[11]。由于轨道交通客流具有显著的非线性特征，这些方法对于复杂的交通流量预测效果不佳。基于非线性模型和机器学习的方法可以有效提取不同类型日期的地铁客流量的周期性及非线性特征，从而提高轨道交通客流的预测精度[12-13]。邵必林[12]提出融合季节差分自回归移动平均模型（seasonal autoregressive integrated moving average model，SARIMA）和支持向量机（support vector machine，SVM）的优化模型，采用SARIMA对地铁客流量的时间序列数据进行线性建模，使用SVM对SARIMA模型输入的残差值进行非线性建模。基于实际数据的实验结果表明，SARIMA-SVM模型的预测精度高于单一模型，精度提高了12.24%。Roos[14]提出了一种基于动态贝叶斯网络来预测城市轨道网络短期客流的方法，该方法在即使数据不完整的情况下也可进行推演，模型在预测精度、泛化能力方面都表现良好。深度学习作为机器学习的一个分支，通过端到端的学习框架，可以有效提取高层次特征，其良好的预测性能促进了交通预测领域的革新。深度學习算法被应用到城市轨道交通出行需求预测的研究中，通过设计不同的深度神经网络结构，提取时空出行需求特征[15-18]。

城市轨道交通站点的出行需求预测包括进站量和出站量的预测。传统的方法都是基于提出的模型对站点的短时进站量和出站量分别进行预测，将出行需求预测当作单个的预测任务，忽略了出行进出站量预测之间的内在联系。此外，缺乏对交通数据的时空特征和动态相关性进行建模以及外部变量的有效利用，使得预测模型效果的提升达到瓶颈。针对上述问题，本研究基于历史进站客流刷卡数据，提出了基于多任务学习的轨道交通短时客流预测模型，以提取乘客出行数据中的时空出行规律，挖掘出行数据中包含的隐藏特征。模型使用残差卷积神经网络（residual convolutional neural network，ResCNN）处理地铁网络拓扑结构和空间出行特征，采用嵌套式长短期记忆神经网络（nested long short-term memory，NLSTM）和注意力机制捕捉前后关联和复杂时变的时间特征。同时引入列车时刻表数据、公交站点分布数据、POI数据，以预测轨道交通短时进出站客流需求。

1 模型与方法

1.1 问题描述

多任务学习（multi-task learning，MTL）是机器学习中的一种学习范式，是解决联合预测问题的一个很好的方案。本文采用多任务学习的方法，以北京地铁为例，提取轨道交通站点短时进站客流和出站客流预测任务之间的相关性。假设xti，m表示时间间隔t内站点i的短时进出站客流量，这里的m可以表示预测任务，即进站客流量预测任务或者出站客流量预测任务，Xtm表示时间间隔t内地铁站点的客流出行量集合。因此，基于多任务学习的轨道交通短时客流预测问题可以定义为，考虑到当前时间间隔t之前的站点进出站客流量即［Xt-Pm，…，Xtm］和外部特征Et，预测下一个或者未来多个时间间隔Xt+Tm的进站和出站客流量，见公式1。

Xt+1m，…，Xt+Tm=FXt-Pm，…，Xtm，Et，（1）

其中P表示用于预测的历史时间步长，T表示预测的时间步长。

1.2 空间特征提取

为了学习轨道交通客流数据所蕴含的时空特性，卷积神经网络（convolutional neural network，CNN）可以用来捕捉不同站点客流之间潜在的空间关系。然而，随着CNN深度的增加，网络模型出现了“退化现象”。训练集的误差在下降到一定程度会出现反弹，空间特征的提取效果反而越差，这是由于网络的加深而造成的梯度爆炸和梯度消失的问题。构建残差卷积神经网络（residual convolutional neural network，ResCNN），将残差单元（residual unit）嵌入到网络结构中，借鉴了跨层连接的思想，具体方法是在每层网络的输入和输出之间添加一条跳跃连接，将底层的部分特征直接映射到高层网络中，有效缓解了多层神经网络出现的训练退化现象，如图1所示，残差网络的计算见公式2。

Xl+1=RXl，θl+Xl，  （2）

其中，Xl+1和Xl分别表示残差单元的输入和输出，R为残差函数。θl包含了残差单元所有的可学习参数。采用批处理归一化层（batch normalization，BN）对输入数据进行标准化处理，在残差单元中加入卷积层（convolutionlayer，Conv）来提取站点间乘客出行需求的空间特征。ResCNN的应用有效缓解了深度网络存在的梯度消失和爆炸的问题，增强了训练过程中的稳定性，进而提升网络的学习能力。

1.3 时间特征提取

循环神经网络（recurrent neural network，RNN）是一种处理时序型输入的神经网络。RNN在捕获时间特征方面表现出很强的能力，但RNN在误差梯度经过多个时间步的反向传播后，容易发生梯度消失或梯度爆炸现象，即无法对长期记忆的信息进行有效的提取和储存。对于轨道交通短时客流预测任务中时间特征的提取，长短期记忆神经网络（long short-term memory，LSTM）通过门控制结构，调节记忆单元内部状态与其输入输出的相互作用，可以实现对关键信息的长期记忆。

本研究采用嵌套式LSTM神经网络（Nested LSTM，NLSTM）结构来捕获乘客出行需求的时间特征。与通过堆叠结构来增加LSTM神经网络深度的结构不同，NLSTM的嵌套式结构如图2所示。NLSTM神经网络通过引入多层LSTM结构和共享参数的方式，提高了神经网络建模的能力，加快了训练速度，同时降低了过拟合的风险。如图2所示，NLSTM神经网络使用了LSTM神经网络结构，取代了传统LSTM神经网络中的记忆单元，实现了在LSTM神经网络中嵌套一个LSTM神经网络的结构。在NLSTM中，内部记忆单元的访问和信息的传递同样被输入门、遗忘门等单元所控制，以便长期信息只在有相关条件的情况下才选择性的通过，可以更有效地捕捉对时间特征的长期依赖性。

内部LSTM结构的记忆单元状态和门控制单元的公式与标准LSTM神经网络类似，如公式3～7所示。其中带上标“～”的参数属于内部LSTM单元。

由于内部存储单元的存在，外部LSTM神经网络的记忆单元ct状态信息更新过程见公式（10）。外部LSTM神经网络其他门控单元的更新方式与传统的LSTM神经网络一致。

引入注意力机制（attention mechanism）从历史时间步中提取重要的时间特征。在基于注意力的NLSTM神经网络（Attention NLSTM）的结构中，L（·）是个可学习函数，对于输入的不同历史时间步出行需求分配不同的注意力权重，WA和bA分别是可训练的权重和偏置项。对于NSLTM神经网络的输出γN，采用训练的注意力权重α进行加权，使得模型的训练更专注于输入数据中与当前预测输出相关的信息，计算方法见公式（11）～（12），其中⊙表示矩阵元素乘积。

1.4 外部特征提取

轨道交通运营具有鲜明的特点，例如，与公共汽车相比，列车按照精确的时刻表运行。对于乘客来说，乘客会在列车快要到站时，陆续进站到达站台准备上车，此时进站客流会出现一定的小高峰波动。同时，为了运力和运量的良好匹配，在编制列车运行时刻表时便会充分考虑时段客流量多少，在一定时间窗内列车排班到站数目越多，该时间窗内进站客流量就会相对越大。因此，本文将单位小时内上行方向和下行方向到站列车数目作为外部变量加入预测模型中。Ns，t表示站点s在时段t的列车到站数目，其中Nus，t表示站点s在时段t的上行方向列车到站数目，Nds，t表示站点s在时段t的下行方向列车到站数目，见公式13。

Ns，t=Nus，t，Nds，t。（13）

轨道交通因其具有运量大、正点率高、速度快等优势，在一定程度上满足了城市居民的日常出行需求，但在站点位置和乘车线路方面具有一定的局限性，在人们通勤出行中，通常与公交、共享单车等进行接驳。因此，轨道交通站点周边公交站点的分布和数量对地铁客流有着一定的影响。本研究引入轨道交通站点周围公交站点数目作为外部变量，其中Bs，1、Bs，2、Bs，3表示轨道交通站点s周边500、1 000、1 500 m范围内公交站点数目，见公式14。

Bs=Bs，1，Bs，2，Bs，3。（14）

POI兴趣点是地理信息系统范畴中的一个概念，指一些与人们生活密切相关的地理实体，如学校、银行、餐馆、医院、超市等。区域中POI兴趣点的分布可以在一定程度上反映出区域的土地利用特征。轨道交通站点的客流情况与该站点周边的设施息息相关。如果某地铁站点周边居民小区分布较多，那么该地铁站点的客流会以早晚通勤客流为主；如果该地铁站点周边餐饮行业较多，那么该地铁站点会在用餐时间段内客流量较大。本研究采用爬虫技术获取高德地图开放平台的POI数据，来表示轨道交通站点周边的土地使用情况，以提高轨道交通客流预测的精度。Ps表示站点s周围POI类别数量，其中，交通设施＼汽车服务类用Ps，tra表示，餐饮服务类用Ps，din表示，商业类用Ps，biz表示，风景名胜类用Ps，int表示，住宅服务类用Ps，res表示，政府＼金融類用Ps，gov表示，见公式15。

Ps=Ps，tra，Ps，din，Ps，biz，Ps，int，Ps，res，Ps，gov。（15）

1.5 多任务学习与模型融合

对于轨道交通短时客流预测，绝大多数的研究都是通过单任务学习的方式，对于单个不同的学习任务，建立深度学习神经网络模型。参考人类感知和学习模式的特点，研究者们提出了多任务学习的概念，如图3所示。多任务学习采用并行训练多个相关任务的方式对子问题进行建模，在网络结构、输入数据、训练方式等方面存在差异，需要采用更复杂的网络结构和联合训练的方式，以便共享知识和信息，提高模型的泛化能力。同时，由于多任务学习在相关任务间共享网络参数，因此采用多任务学习方式构建的模型训练参数较少，模型的训练过程更加高效。

本节提出了基于多任务学习的时空神经网络模型（multi-task learningbased spatiotemporal neural network，MLT-STNN），来预测轨道交通短时进站客流和出站客流，模型的框架如图4所示。MLT-STNN模型采用编码器-解码器结构建立一种端到端的学习框架，在编码过程中采用ResCNN模块对站点的进站客流［Xt-Tinflow，…，Xtinflow］和出站客流［Xt-Toutflow，…，Xtoutflow］的空间特征进行提取，采用LSTM神经网络对外部特征包括时刻表特征Ns，t、周边公交站分布特征Bs和区域的土地利用特征Ps进行提取。在解码过程中，使用特征融合层对提取的特征进行连接，采用基于注意力的NLSTM神经网络对融合的特征变量进行解码，使得预测模型在不同预测任务之间的信息相互共享，以预测地铁网格中各个站点的进站量X︿t+1inflow和出站量X︿t+1outflow。在模型的训练过程中，采用Adam优化器对提出的MLT-STNN模型进行优化，模型的损失函数为平均绝对误差（mean absolute error，MAE）。

2 客流时空特征分析

采用北京市一个月的地铁刷卡数据集，对提出的MLT-STNN预测模型的性能进行测试，每条记录包含乘客ID、刷卡进站时间、进站站点编号、刷卡出站时间、出站站点编号等。在数据处理的过程中，将该数据进一步分为两组：前24 d的数据作为训练数据集，后7 d的数据作为测试数据集。在数据实验过程中，测试了多个预测时间粒度下，所提出MLT-STNN模型的预测性能，例如10、30、60 min。对于历史出行需求等连续型变量，采用min-max归一化方法，处理后数据范围为0，1。对于分类变量，如站点周边土地利用类型，需要将其转换为独热编码（one-hot encoding）处理。

对历史乘客刷卡出行数据进行分析，图5显示了不同功能区站点的进站客流时间分布。总体来说，在住宅区和餐饮区的客流出行量较大，在风景名胜区的客流出行量较小。在住宅区，工作日（周一至周五）早上7点到9点之间出现进站的高峰，这种规律很符合乘客乘坐地铁进行通勤的出行行为，然而在周末这种出行特征消失。在餐饮区，休息日（周六至周天）11点起进站量开始逐渐增多，大部分市民在周末到餐饮区进行休闲活动，相较于工作日出行量明显增大。不同功能区站点进站客流的出行特征不同，因此，短时客流预测需要考虑站点周边的土地利用特征。图6反映了地铁站点的进站客流的空间分布，其中包括工作日的高峰和平峰、休息日高峰和平峰。可以看出，在工作日的高峰，地铁客流进站量较大，其中在大望路、国贸、西单等地铁换乘站，客流量较大。因此，需要对大客流站点的短时出行需求进行准确预测，有利优化行车组织和客流管控，以寻求运力、运量的最优匹配。

3 实验结果分析

3.1 算法预测精度对比

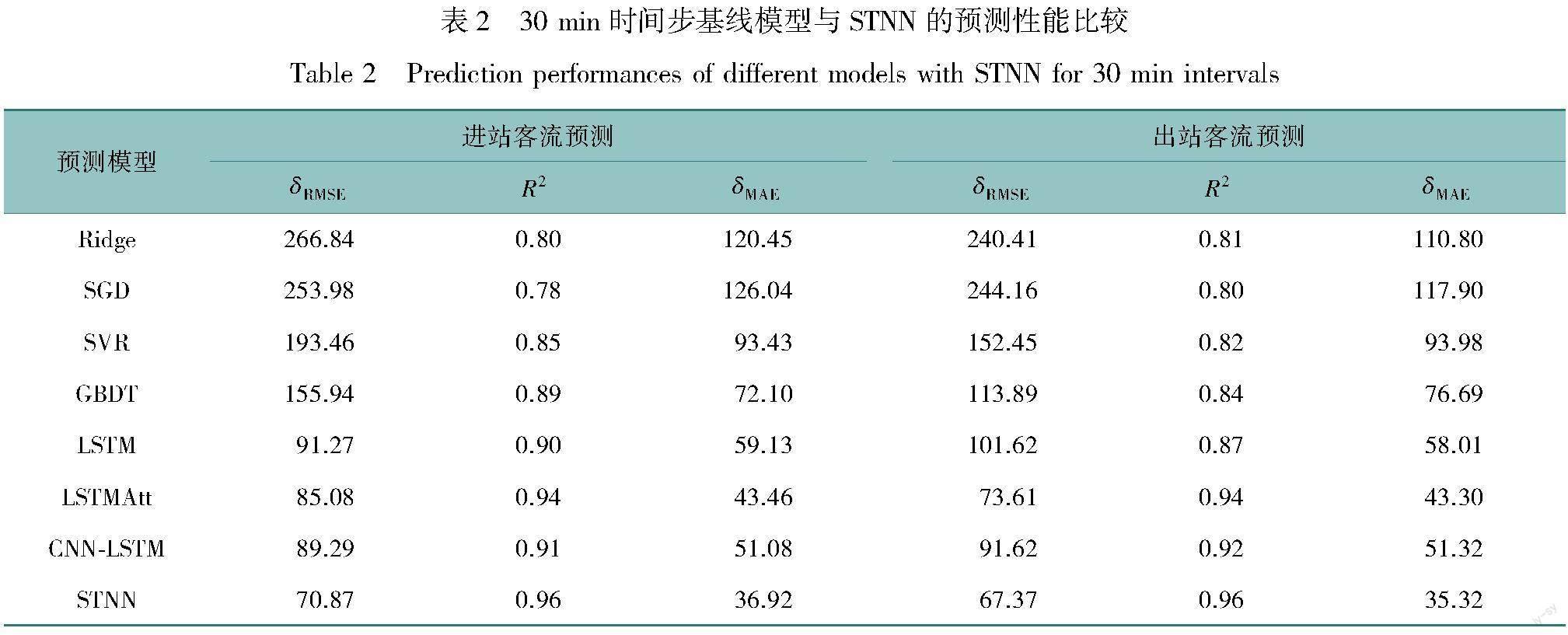
在不同时间粒度上，例如10、30、60 min，模型预测精度的对比见表1～3。

实验结果表明，机器学习和深度学习算法具有更强的非线性拟合能力，在短时出行需求预测任务上表现的更好。例如，在10 min时间间隔的进站客流预测任务中，Ridge模型的δRMSE为47.66，SGD模型的δRMSE为49.52，SVR模型的δRMSE为42.46，GBDT模型的δRMSE为39.76。机器学习SVR模型和GBDT模型可以处理预测任务中的时空非线性关系，预测性能相较于统计学模型有所提升。深度学习LSTM模型通过引入了门控单元结构来有选择性地提取历史时间步的出行需求信息，δRMSE降低为38.49，δMAE降低为20.00。LSTMAtt在LSTM模型中引入了注意力机制，使得模型更好的提取时间特征的相关性，预测误差δRMSE为33.79，R2指标为0.92。CNN-LSTM 模型采用CNN和LSTM对客流的时空特征进行提取，预测误差δRMSE为29.81。STNN模型考虑对时空出行特征的提取，预测误差δRMSE降低为24.02，R2指标提升为0.96，这表明时空相关性的提取在地铁短时出行需求预测中发挥重要作用，其中ResCNN结构和基于注意力的NLSTM结构可以更好地对预测任务的空间相关性和时间相关性进行提取。

本文所提出的STNN模型，在不同时间粒度下的客流预测都有较高的預测精度。例如，在10、30、60 min的进站客流预测任务中， LSTM模型的预测误差δMAE指标为20.00、59.13和112.07。LSTMAtt模型的预测误差δMAE指标为16.99、43.46和75.13，预测误差分别减少15.05%、26.50%和32.96%。STNN模型通过残差单元嵌入到网络结构中，实现了CNN网络的跨层连接，预测误差δMAE指标降低为13.56、36.92、64.33，相比于LSTMAtt模型预测误差减少20.18%、15.04%和14.37%。在预测模型的时间复杂性上，Ridge模型和SGD模型预测所需的时间最短，但预测误差较大。机器学习模型SVR模型和GBDT模型，预测时间比传统的统计学模型的预测时间要长。由于需要提取时空特征和外部特征，所提出的STNN模型比LSTM模型和CNN模型需要更长的训练时间，但融合了较为丰富的时空特征以及外部环境特征，STNN模型表现出了良好的预测精度和鲁棒性。因此，STNN模型可以在预定的时间内，准确预测轨道交通客流短时进出站量。

3.2 多任务学习算法预测结果

在多任务学习的实验中，通过对MTL-LSTM模型、MTL-CNN-LSTM模型和MTL-STNN模型预测性能的比较（表4），发现多任务学习结构可以进一步提高轨道交通短时进出站客流预测任务的精度。轨道交通进站客流和出站客流之间确实具有显著的依赖性，这可以通过多任务学习方法来提取相关任务之间的内在关联关系。例如，在30 min的地铁进站客流预测任务中，采用LSTM模型，预测误差δRMSE和δMAE的值为91.27和59.13。多任务学习MTL-LSTM模型通过考虑进出站客流预测任务的相关性，预测误差δRMSE和δMAE降低为88.44和49.86。MTL-STNN模型在多任务学习框架下，考虑对乘客出行时空特征的提取。例如，在30 min的需求预测中，对于进站客流的预测任务，MTL-STNN模型预测误差δRMSE和δMAE为56.79和28.14，与STNN模型相比，预测误差降低24.79%和23.78%。在测试集上，多任务学习模型预测精度对比如图7所示，可以看出基于多任务的深度学习模型可以更加准确地预测轨道交通乘客短时出行需求。

4 结论

本文主要研究了轨道交通短时客流预测任务，提出了一种基于多任务学习的时空神经网络模型。该模型采用残差卷积神经网络和嵌套式长短期记忆神经网络提取地铁客流的时空相关性，引入注意力机制加强模块对特征的提取效果。考虑到地铁运营的特点，选取列车运行特征、轨道交通站点周边公交站点以及兴趣点数据作为外部特征，以提高模型的预测精度。基于北京地铁的乘客刷卡数据，本文首先分析了用户出行需求的时间特征和空间特征，以及在工作日和周末不同功能区域的乘客出行模式。基于乘客刷卡数据，在不同时间粒度的预测任务上进行实验，融合多源数据以提高不同时段客流预测的准确度。与基准模型包括数理统计的模型和机器学习模型的预测性能相比，本文提出的MTL-STNN模型，采用定制化的神经网络提取模块，同时考虑了对时空出行特征的提取，并通过多任务学习方法刻画进站客流和出站客流之间的相关性，模型表现出了良好的预测精度和鲁棒性。未来将进一步研究面向大规模城市轨道交通网络以及多场景的短时客流预测，为客流管控和行车调度提供更丰富的数据基础。

参考文献：

［1］中国城市轨道交通协会. 城市轨道交通2021年度统计和分析报告. [EB/OL]. [2022-04-22]. https：//www.camet.org.cn/tjxx/9944

[2]李梅， 李静， 魏子健， 等. 基于深度学习长短期记忆网络结构的地铁站短时客流量预测[J]. 城市轨道交通研究， 2018， 21（11）： 42-46. DOI： 10.16037/j.1007-869x.2018.11.009.

[3]LIU Y， LIU Z Y， JIA R. DeepPF： A deep learning based architecture for metro passenger flow prediction[J]. Transportation Research Part C： Emerging Technologies， 2019， 101： 18-34. DOI： 10.1016/j.trc.2019.01.027.

[4]施俊庆， 李睿， 程明慧， 等. 基于动态时空神经网络模型的地铁客流预测[J]. 交通运输系统工程与信息， 2023， 23（2）： 139-147. DOI： 10.16097/j.cnki.1009-6744.2023.02.015.

[5]赵阳阳， 夏亮， 江欣国. 基于经验模态分解与长短时记忆神经网络的短时地铁客流预测模型[J]. 交通运输工程学报， 2020， 20（4）： 194-204. DOI： 10.19818/j.cnki.1671-1637.2020.04.016.

[6]LI Y， WANG X D， SUN S， et al. Forecasting short-term subway passenger flow under special events scenarios using multiscale radial basis function networks[J]. Transportation Research Part C： Emerging Technologies， 2017， 77： 306-328. DOI： 10.1016/j.trc.2017.02.005.

[7]XUE G， LIU S F， REN L， et al. Forecasting the subway passenger flow under event occurrences with multivariate disturbances[J]. Expert Systems With Applications， 2022， 188： 116057. DOI： 10.1016/j.eswa.2021.116057.

[8]赵建东， 朱丹， 刘佳欣. 基于时间序列分解与门控循环单元的地铁换乘客流预测[J]. 华南理工大学学报（自然科学版）， 2022， 50（5）： 22-31. DOI： 10.12141/j.issn.1000-565X.210559.

[9]惠阳， 王永岗， 彭辉， 等. 基于优化PSO-BP算法的耦合时空特征下地铁客流预测[J]. 交通运输工程学报， 2021， 21（4）： 210-222. DOI： 10.19818/j.cnki.1671-1637.2021.04.016.

[10]LI C， BAI L， LIU W， et al. A multi-task memory network with knowledge adaptation for multimodal demand forecasting[J]. Transportation Research Part C： Emerging Technologies， 2021， 131： 103352. DOI： 10.1016/j.trc.2021.103352.

[11]李德奎， 杜书波， 张鹏. 基于ARIMA和LSTM的城市轨道交通延时客流预测方法比较[J]. 青岛理工大学学报， 2021， 42（4）： 135-142. DOI： 10.3969/j.issn.1673-4602.2021.04.020.

[12]邵必林， 饶媛， 何欣. 基于SARIMA-SVM组合模型的地铁客流量预测研究[J]. 软件导刊， 2022， 21（11）： 24-30. DOI： 10.11907/rjdk.212729.

[13]韩皓， 徐圣安， 赵蒙. 考虑线网结构的LightGBM轨道交通短时客流预测模型[J]. 铁道运输与经济， 2021， 43（10）： 109-117. DOI： 10.16668/j.cnki.issn.1003-1421.2021.10.17.

[14]ROOS J， GAVIN G， BONNEVAY S. A dynamic Bayesian network approach to forecast short-term urban rail passenger flows with incomplete data[J]. Transportation Research Procedia， 2017， 26： 53-61. DOI： 10.1016/j.trpro.2017.07.008.

[15]CHEN P F， FU X D， WANG X. A graph convolutional stacked bidirectional unidirectional-LSTM neural network for metro ridership prediction[J]. IEEE Transactions on Intelligent Transportation Systems， 2022， 23（7）： 6950-6962. DOI： 10.1109/TITS.2021.3065404.

[16]沈永發， 郑煜， 刘辉冉， 等. 基于历史数据的轨道交通站内客流预测模型[J]. 武汉理工大学学报（信息与管理工程版）， 2022， 44（6）： 887-893. DOI： 10.3963/j.issn.2095-3852.2022.06.003.

[17]王金水， 欧雪雯， 陈俊岩， 等. 基于组合模型的城市轨道站点短时客流分类预测[J]. 铁道科学与工程学报， 2023， 20（6）： 2004-2012. DOI： 10.19713/j.cnki.43-1423/u.t20221280.

[18]张金雷， 陈奕洁， Panchamy Krishnakumari， 等. 基于注意力机制的城市轨道交通网络级多步短时客流时空综合预测模型[J]. 地球信息科学学报， 2023， 25（4）： 698-713.