中心不重合径向剪切干涉迭代波前重构算法仿真分析

杜旭升，白福忠,2，徐永祥,2，王建新

（1.内蒙古工业大学 机械工程学院，内蒙古 呼和浩特 010051；2.内蒙古自治区特殊服役智能机器人重点实验室，内蒙古 呼和浩特 010051；3.西南科技大学 极端条件物质特性联合实验室，四川 绵阳 621010）

引言

干涉测量技术因具有非接触测量、测量精度高的优点而备受人们关注[1]。其中，径向剪切干涉是一种自参考干涉技术，与传统双光束干涉相比，具有不需要额外设置参考光路、干涉系统易于设计成共光路结构等优势[2]，从而对温度变化、空气扰动、振动等因素不敏感，被广泛应用在自适应光学[3]、激光波前诊断、光学元件质量检测、角膜地形图测量、温度场测量、流场测量[4]等领域。但是与传统含有绝对平面波前参考光束的干涉技术相比，径向剪切干涉所形成的相位差并不是待测波前相位本身，而是待测波前的扩束和缩束波面在重叠区域的相位差[5]。因而如何从相位差信息中获取待测波前相位，即波前重构，是径向剪切干涉中的一个重要研究内容。

目前波前重构算法主要包括迭代重构算法和模式重构算法[6]。迭代重构算法是将剪切波前经过若干次插值放大，将所有迭代结果与原始相位差数据相加得到重构波前。迭代重构算法原理简单，实际应用可行性好，对待重构的波前畸变的空间频率信息没有特别要求。模式重构算法用Zernike、Legendre 多项式作为模式基底，分别对圆形孔径或方形孔径相位差数据进行模式拟合而得到重构波前[7]，模式法适用于重构低空间频率的波前畸变，对于高空间频率的像差复原精度较低。

对于传统波前重构算法，从重构原理上讲均要求扩束与缩束光波中心重合或对准，否则会产生重构误差。然而，在实际的径向剪切干涉测量实验中，为了使扩束与缩束光波中心对准，需要多次反复地对光学系统进行精密调试，使扩束与缩束光波中心尽可能重合，增加了实验调试复杂性。尽管如此，实际上很难保证中心严格重合，而中心不重合情况却时有发生。另外，对于不同结构类型的径向剪切干涉系统，其调整方法也不尽相同，因而很难设计出通用且行之有效的装调技术。

为此，若能够通过实验方式检测出中心偏移量大小，考虑将其作为一个新的物理变量引入到波前重构算法中，由此获得高精度波前重构结果，对于降低调试难度、提高测量效率、保证测量精度具有重要意义。因此，研究适用于中心不重合情况下的波前重构算法就成为一个重要且有意义的内容。目前关于改进的迭代波前重构算法要求扩束比与缩束比成倒数关系，仅适用于特定光学结构系统，如环路径向剪切干涉仪[8]。而对于如文献[9]的系统则无法适用，算法普适性差。

本文基于传统迭代重构算法，推导了更具普适性的中心不重合径向剪切干涉迭代波前重构算法，给出了详细的算法设计方案。仿真分析了本文算法与传统迭代波前重构算法在Zernike 组合像差、单阶Zernike 像差、中心偏移程度及其计算误差情况下的重构效果，验证了本文算法的有效性与可靠性。

1 用于中心不重合径向剪切干涉的迭代波前重构算法原理

径向剪切干涉是利用剪切干涉装置把待测波面分成扩束、缩束两个相干波面，使两个波面在空间重叠区域发生干涉；通过相位复原算法从干涉条纹中求解剪切相位差，进而利用波前重构算法计算出被测波前相位[10]。图1 是径向剪切干涉示意图，设缩束比为sc（sc＜1），扩束比为se（se＞1），则剪切比 β=sc/se。

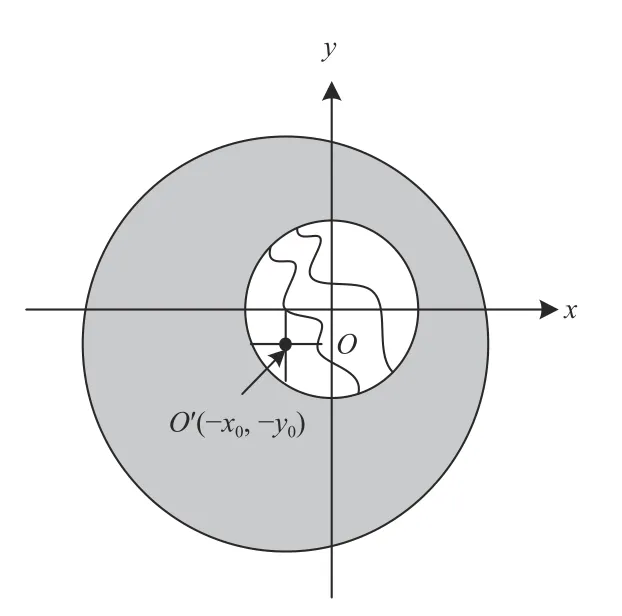
图1 径向剪切干涉示意图Fig.1 Schematic diagram of radial shearing interference

设原始波面方程为W(x,y)，将坐标系原点O定义在缩束波面的中心位置，扩束波面中心O'相对于缩束波面中心的偏移量为 (-x0,-y0)，为了便于推导，可先假设y0=0。于是缩束波面可表示为W(x/sc,y/sc)，扩束波面可表示为W(x/se+x0,y/se)，则两波面在重叠区域的相位差可表示为

式（1）中坐标变量x和y乘以β可以使扩束波面中心区域逐渐趋近平面波：

重复上述过程可得：

式中：n=0,1,2,···,N，表示迭代次数。为了消除式（1）至式（4）等号右边第2 项，在式（2）中增加坐标变量x0后变为

式（3）中增加坐标变量 (β+1)x0后变为

式(1)、式(5)至式(7)相加，等号两边各项错位相消后可得：

经过若干次迭代，扩束波面的中心区域趋近平面波，因而上式最后一项可以被忽略，于是式（8）可写为

进一步地，若y0≠0时可以得到迭代重构波前的一般表达式：

若剪切光束中心重合，则x0=y0=0，代入式（10）推导出如下所示中心重合情况下的迭代波前重构表达式，这与传统迭代重构算法是一致的。

2 波前重构算法实现步骤

用于中心不重合径向剪切干涉的迭代波前重构算法实现过程主要包括相位差复原、干涉图参数求解、迭代波前重构3 个技术步骤。

1）剪切相位差复原

利用径向剪切干涉系统，引入相位调制技术，获取载波干涉条纹图像或者移相干涉图[11]。对于载波干涉条纹，仅需一帧条纹图像便可采用傅里叶变换算法求解剪切相位差。对于移相波前复原技术而言，常用四步移相算法[12]，相邻两帧移相干涉图之间的相移量为 π/2，仿真的四帧移相径向剪切干涉图如图2 所示。

图2 仿真的四步移相径向剪切干涉图Fig.2 Simulated four-step phase-shifting radial shearing interferograms

四步移相算法表示为

式中：Ik（k=1，2，3，4）为移相干涉图强度。对式（12）计算出的包裹相位经过相位解包裹[13]后得到剪切相位差 ΔW，即扩束光波和缩束光波在重叠区域的相位差。

2）干涉图参数求解

由扩束光波的半径re和缩束光波的半径rc，计算剪切比 β=rc/re。两光波中心坐标之差即为中心偏移量 (x0,y0)。

3）迭代波前重构

基于上节介绍的迭代波前重构算法原理，将迭代重构实施过程归纳为如下5 个步骤。

a）将剪切相位差 ΔW通过插值运算扩大1/β倍，得到扩束波面。

b）以扩束波面中心为基准，引入中心偏移量 (x0,y0)，在扩束波面中提取有效数据区域。有效数据区域大小与剪切相位差大小一致，由此得到第1 次迭代波面，记为 ΔW1。

c）将 ΔW1扩大1/β倍得到新的扩束波面。重复步骤b)，得到第2 次迭代波面 ΔW2。

d）重复上述迭代过程N次，得到第N次迭代波面 ΔWN与第N-1 次迭代波面 ΔWN-1，若迭代结果满足式(13)，则迭代过程终止[14]。

式中：Num表示 ΔWN中包含的有效数据个数；λ为光波的波长。

e）将剪切相位差 ΔW与N次迭代波面相加，得到重构波面W：

迭代波前重构算法实现流程如图3 所示。图中虚线所示的圆形区域表示未考虑中心偏移时提取的有效数据范围，实线所示的圆形区域表示考虑中心偏移后提取的有效数据范围。

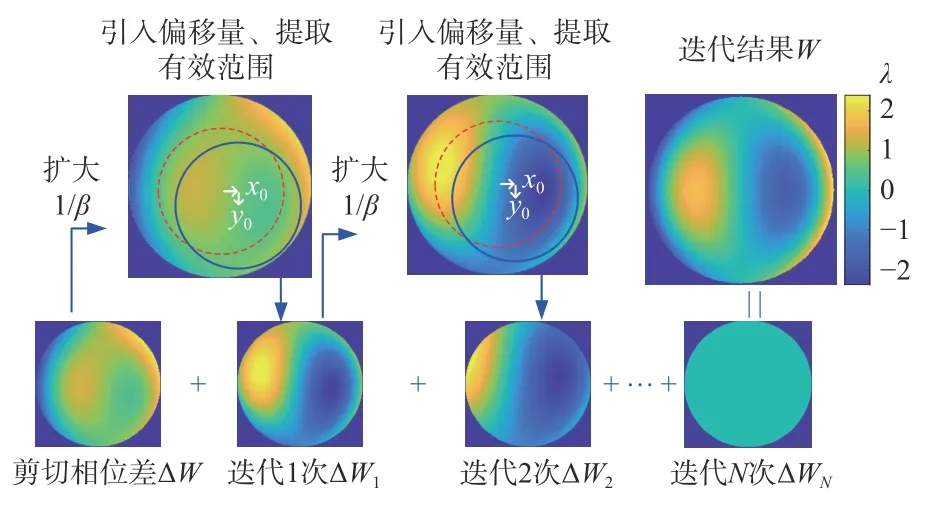
图3 迭代波前重构算法实现流程Fig.3 Implementation flow of iterative wavefront reconstruction algorithm

3 波前重构算法仿真分析

3.1 算法有效性验证

首先对本文算法的有效性进行验证，取3 至15 阶圆形孔径Zernike 多项式构造组合像差，得到原始仿真波面如图4(a)所示，大小为256×256像素。

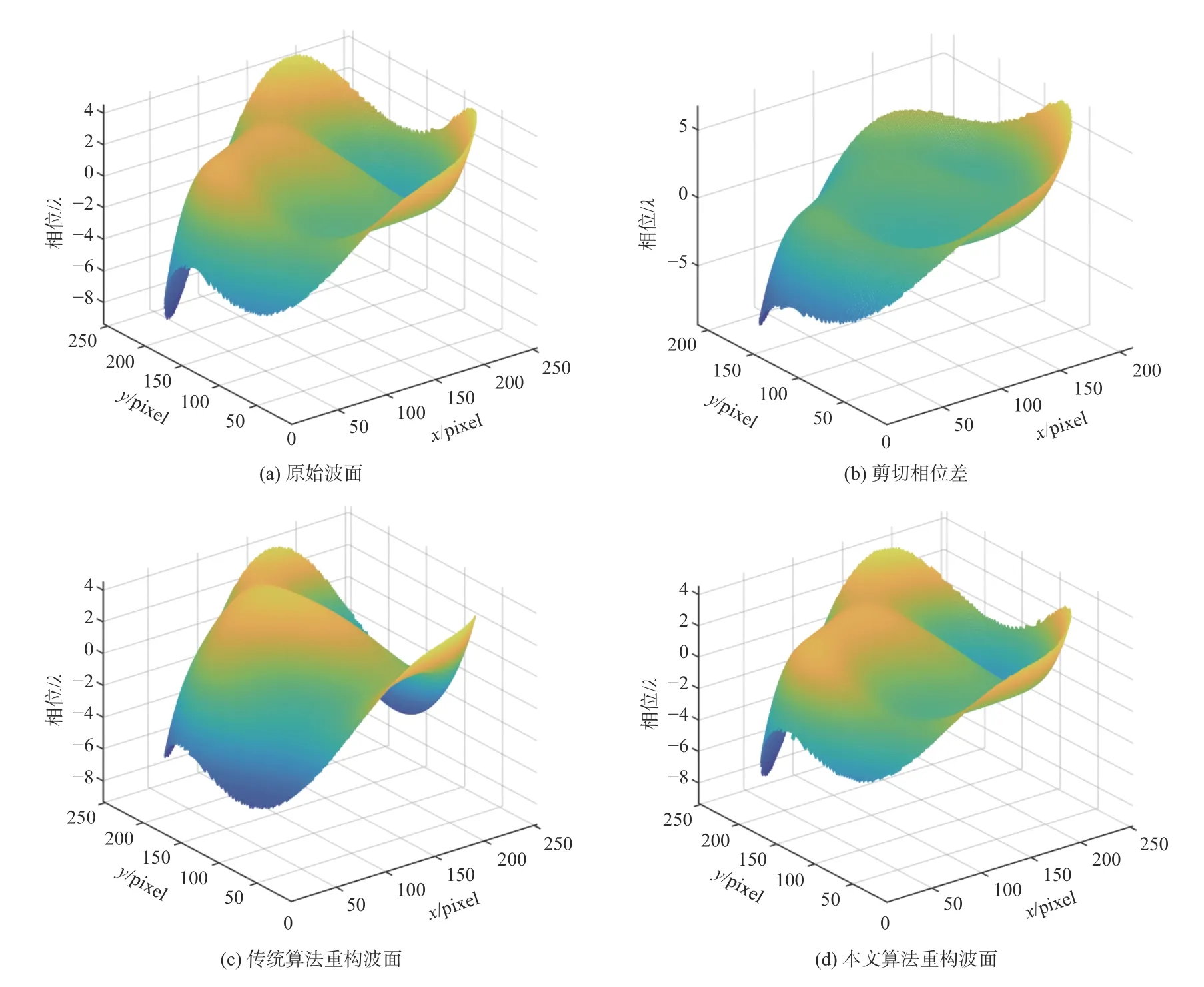
图4 两种算法重构结果对比Fig.4 Comparison of reconstruction results of two algorithms

假设缩束比sc=0.828，扩束比se=1.2；中心偏移量y0=0 像素，x0=25 像素。于是可得剪切比β=sc/se=0.69，缩束和扩束波面大小分别为212×212像素和308×308 像素。仿真条件中扩束比与缩束比并非成倒数关系，也可以为其他任意量值。

由缩束与扩束波面相减得到剪切相位差，如图4(b)所示，其大小与缩束波面大小相等。使用传统迭代重构算法对剪切相位差进行波前重构，重构波面与误差波面如图4(c)和图4(e)所示。本文算法得到的重构波面和误差波面如图4(d)和图4(f)所示，其中误差波面是由重构波面与原始波面作差得到。

传统算法重构误差的峰谷(PV)值为3.617 1λ，均方根误差（RMS）值为0.851 9λ，本文算法重构误差的PV 值为0.020 6λ，RMS 值为0.004 6λ，重构误差要远小于传统算法重构误差。

将原始波面、传统算法和本文算法的重构波面的中间一行截面数据（沿x轴方向）绘制于图5。本文算法的重构结果与原始波面高度吻合，而传统算法的重构结果却与原始波面存在明显差异。表明本文算法在存在中心偏移时能够准确地重构出待测波前。

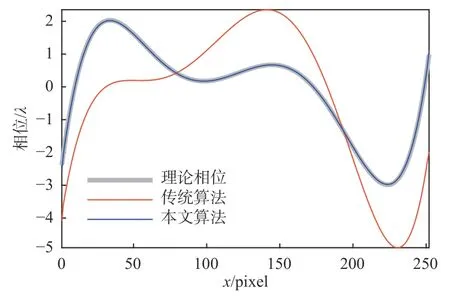
图5 重构波面中间一行截面数据Fig.5 Cross-section data in middle row of reconstruction wavefront

3.2 不同Zernike 像差的重构精度分析

通过对3.1 节得到的重构结果进行Zernike 分解[15]，得到3 至15 阶Zernike 系数，原始波面的Zernike 系数是在仿真时直接给定，如图6 所示。

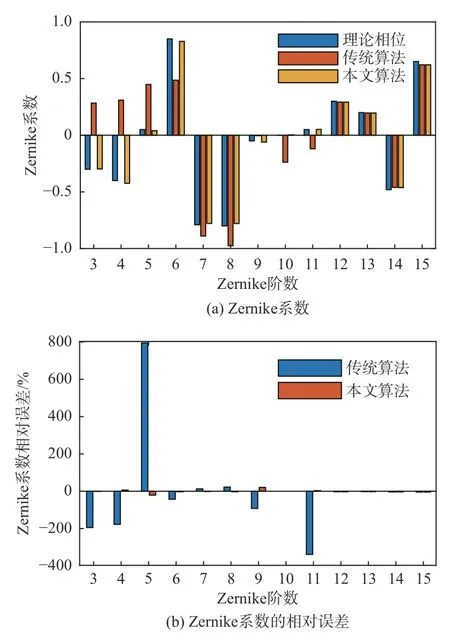
图6 两种算法对各阶Zernike 像差的重构结果对比Fig.6 Reconstruction results comparison of different orders of Zernike aberration with two algorithms

图6(a)显示了原始波面下两种算法重构结果的Zernike 系数柱状图；图6(b)显示了Zernike 系数的相对误差分布，其中相对误差是指重构结果Zernike 系数与理论系数之差与理论系数的比值。结果显示，本文算法对于不同Zernike 像差的重构精度都明显高于传统算法，相对而言，两种算法对第5 阶像差的重构误差偏大，其中传统算法重构相对误差约800%，改进算法重构相对误差为20.7%。

3.3 中心偏移量对重构精度的影响

根据3.1 节仿真条件可知，中心偏移量最大允许值（扩束与缩束波面半径之差）为48 像素。本节通过改变中心偏移量的大小来对重构算法精度进行分析。设中心偏移量沿x方向从0 至48 像素、以2 像素步长逐渐增加，在y方向保持为0，其余仿真条件与3.1 节相同。两种算法得到的重构误差RMS 值如图7 所示。结果显示，随着中心偏移量逐渐增大，传统算法重构误差近似呈线性增大，最大重构误差RMS 值为1.6λ；中心偏移量变化时本文算法的重构误差一直保持在较低水平，最大重构误差RMS 值为0.05λ，说明中心偏移量的大小对本文算法的影响几乎可以忽略。

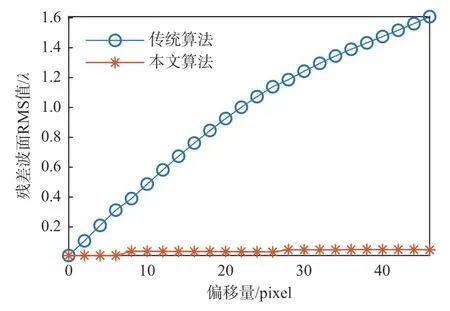
图7 组合像差重构误差随中心偏移量的变化Fig.7 Variation of reconstruction errors of combined aberration with center offset

3.4 单阶Zernike 像差在不同偏移量情况下的重构精度分析

考虑3 至15 阶单阶Zernike 像差，在中心偏移量（y0=0 像素，x0=0～48 像素）由小到大变化过程中的情况，对比分析两种算法的重构效果，图8 给出了两种算法的重构误差RMS 值。本文算法重构误差的RMS 值为10-2λ量级；而传统算法对于各阶Zernike 像差的重构误差普遍较大，重构误差RMS 值约为1λ量级。

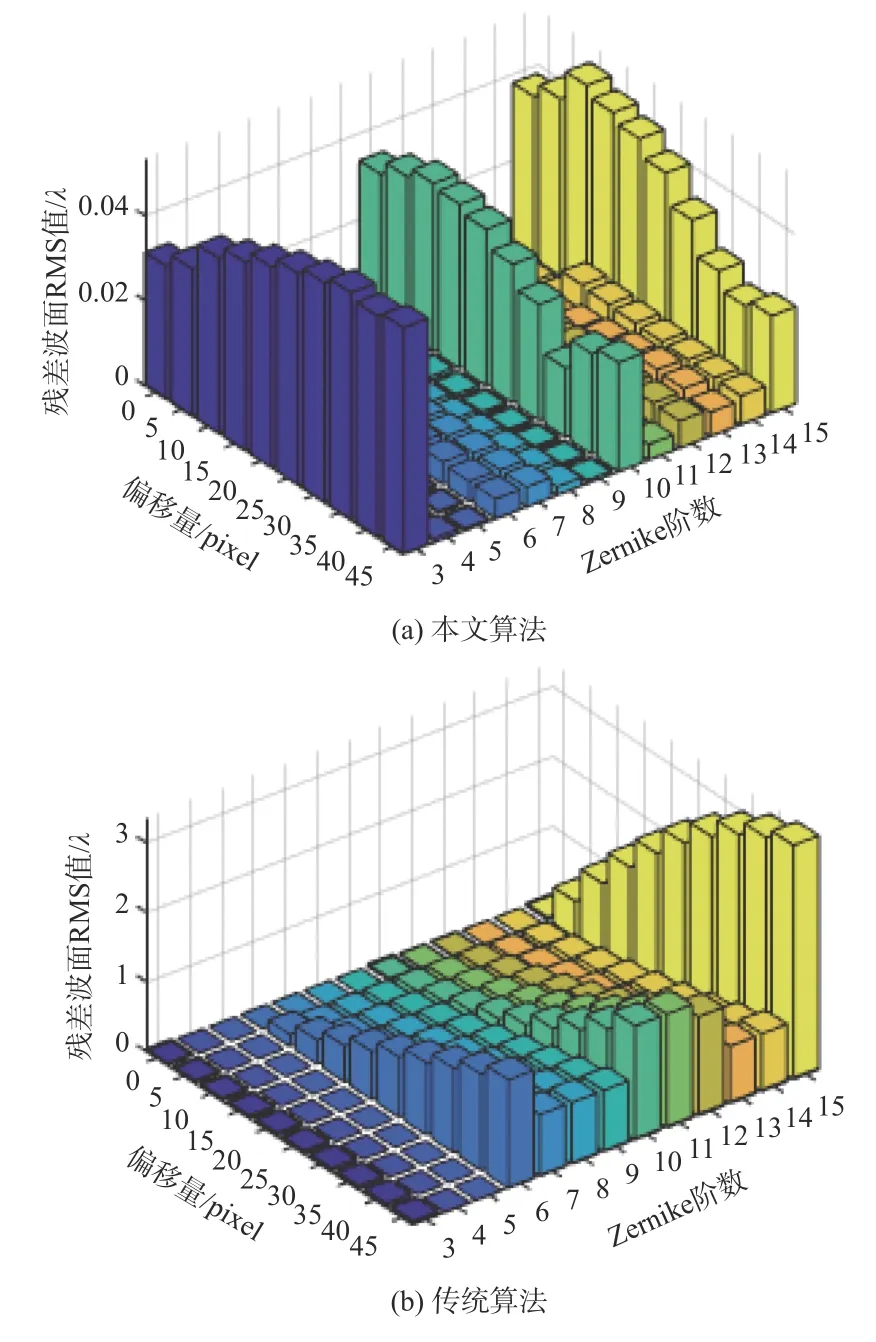
图8 单阶Zernike 像差重构误差随中心偏移量的变化Fig.8 Variation of reconstruction error of single-order Zernike aberration with center offset

图9 显示了重构误差偏大的第3 阶、第10 阶和第15 阶Zernike 像差重构误差RMS 值随偏移量的变化曲线。由图可见，本文算法重构误差最大为0.054λ；而传统算法重构误差随偏移量增加逐渐增大，最大重构误差为3.39λ。

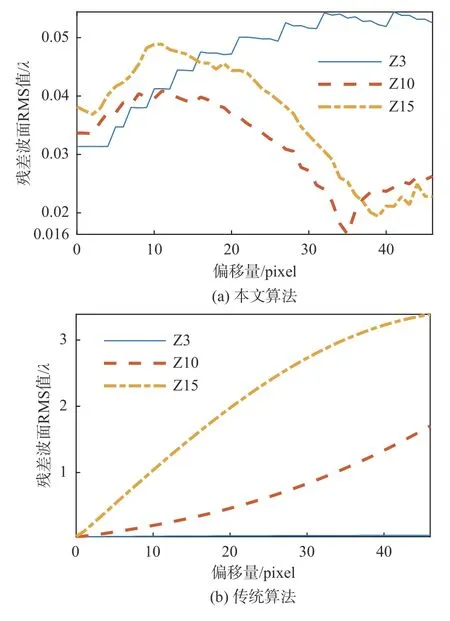
图9 部分Zernike 像差重构误差Fig.9 Reconstruction error of part of single-order Zernike aberrations

综上可知，对于单阶Zernike 像差以及组合像差，不论中心偏移量有多大，本文算法均能获得高精度的波前重构结果。而传统算法未考虑中心偏移情况，其重构误差与中心偏移量近似呈线性关系。

3.5 中心偏移量计算误差对重构精度的影响

对于迭代算法的数学模型，难以从理论推导上分析中心偏移量的计算误差对重构精度的影响，这里同样使用数值仿真方式进行分析。基于3.1节仿真条件，当中心偏移量的计算误差在-20 像素至20 像素范围内变化时，计算出的本文算法重构误差RMS 值如图10 所示。重构误差符合一般常识，即计算误差越大，重构误差越大，这也从侧面说明，中心偏移量的准确计算对提高算法重构精度是重要的。

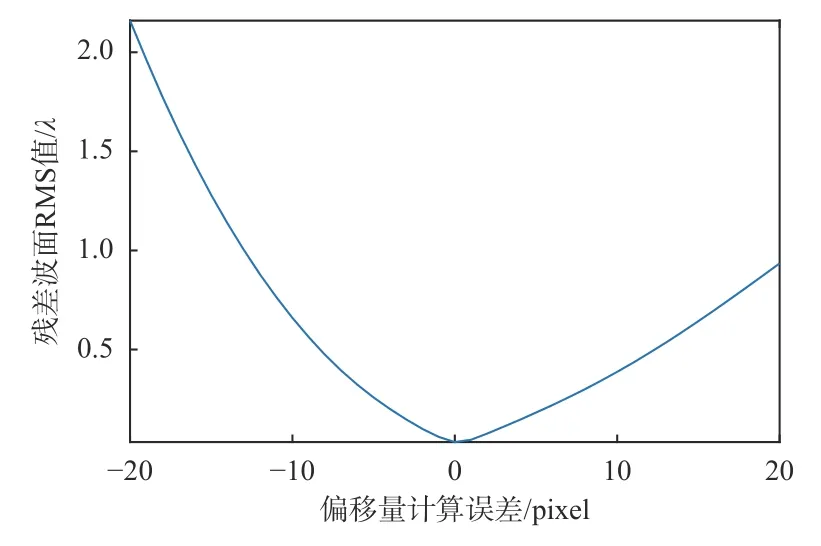
图10 中心偏移量计算误差对波前重构精度的影响Fig.10 Influence of center offset calculation error on wavefront reconstruction accuracy

在实际测量中，可对扩束和缩束光波的光斑图像采用图像处理技术，来获得各自中心坐标，从而计算出中心偏移量。引入本文算法重构被测波面，通过图像处理算法能够更有利于提高并保证测量精度；同时也避免了传统算法需要对光学系统进行反复调试来达到剪切光波中心的准确对准。接下来作者将对实际应用中的剪切光波中心偏移量标定方法进行深入研究，为改进算法的工程化应用提供技术支持。

4 结论

本文基于径向剪切干涉中的迭代波前重构算法，推导了一种更为普适的中心不重合径向剪切干涉迭代波前重构算法。通过数值仿真分析了组合Zernike 像差、单阶Zernike 像差、中心偏移量变化对传统迭代重构算法与本文算法的影响。仿真结果显示，相较于传统重构算法，本文算法的重构精度更高，不受偏移量大小的影响，适用于不同类型的波前像差。这对于传统算法实验调试对准过程繁琐、重构精度难以保证的问题，提供了一种有效解决途径。本文仿真分析是在剪切比、波面大小不变的情况下，仿真分析了中心偏移量、待测波面这些物理量对算法性能的影响，上述的研究结论在其他剪切比、波面大小和波面类型中同样具有普遍意义。另外，两种算法在计算效率方面没有明显优劣。