基于单一元件产生太赫兹无衍射波束技术研究

韩美瑶，郝丛静，黄 倩，涂思语，刘劲松，杨振刚，王可嘉

（1.华中科技大学 武汉光电国家研究中心 光学与电子信息学院，湖北 武汉 430074；2.中国航空工业集团公司北京长城航空测控技术研究所，北京 100111）

引言

1987 年，DURNIN 首次提出了无衍射光束的概念[1-2]，自此无衍射光束成为光学领域研究的热点之一，各种不同的无衍射光束被产生出来，例如贝塞尔光束[1]、马丢光束[3]、艾里光束[4]以及抛物光束[5]等。理论上，无衍射光束是指，在传输过程中横截面光场分布保持不变的光束，即不会发生扩束现象。理想的无衍射光束是不可能实现的，因为它需要占据整个自由空间，且需要无穷的能量。因此在现实中，已产生出的无衍射光束均为准无衍射光束。由于具有无衍射[1]、自修复[6]和提供光学拉力[7]等诸多特性，无衍射光束已经广泛应用于光学操纵[8-9]、光学成像[10-11]、光通信[12-13]、精密测量[14]和激光加工[15]等相关领域。

作为第一个被产生出的无衍射光束，贝塞尔光束是现在应用最多、最为著名的一类无衍射光束。迄今为止，人们已经开发出许多种产生贝塞尔光束的方法，例如环缝法[1]、法布里-珀罗腔[16]、轴棱锥法[17]、超表面法[18-19]、计算机全息技术[20-22]和空间光调制器[23]等。其中轴棱锥法具有制备方法简单、能量转换效率高等优点，被广泛使用。例如在红外、可见光波段，利用抛光工艺人们可以很轻易地获得玻璃轴棱锥[24-25]。对于微波、太赫兹波而言，使用增材制造技术可以快速制备出轴棱锥[26-28]，进而获得长波贝塞尔波束。

实验结果表明，利用单一轴棱锥产生的贝塞尔光束总是紧贴轴棱锥。形像地说，对于轴棱锥而言是没有所谓的“焦距”概念，这一缺点限制了贝塞尔光束的一些实际应用，尤其是一些远程成像和检测应用等。为解决这一问题，2020 年XIANG等人[29]提出了一种透镜——轴棱锥级联结构，产生的米级长度太赫兹无衍射波束不再紧贴产生单元，而是具有百毫米量级的投送距离。需要指出的是，多级联透镜-轴棱锥结构器件数较多，器件间间距较大，因此损耗较大。2022 年，ZHANG 等人[30]研发了一种椭圆轴棱锥，产生出了具有“焦距”的太赫兹“贝塞尔波束”。借鉴ZHANG 等人的设计理念，本文设计并制备出了抛物轴棱锥，同样也产生出了具有“焦距”的太赫兹无衍射波束。利用角谱理论和空间频谱对抛物轴棱锥进行分析，发现抛物轴棱锥与普通轴棱锥的空频形状不同，即抛物轴棱锥产生出的无衍射波束不是普通轴棱锥产生的贝塞尔波束，而是一种全新的无衍射波束——梳状空频无衍射波束。

1 理论设计与仿真计算

普通轴棱锥的横截面是一个等腰三角形，如图1(a)所示。通过在等腰三角形的两个等边上限定抛物线设计轴棱锥结构，称其为抛物轴棱锥，如图1(b)所示。等腰三角形的底边和底角分别为 2R和θ，两个腰的长度为 2a=R/cosθ。当底边 2R和底角θ被确定时，两个腰的长度a也会被确定，此时改变抛物轴棱锥结构的唯一变量为b。在此引入一个无量纲量k=a/b代替b。

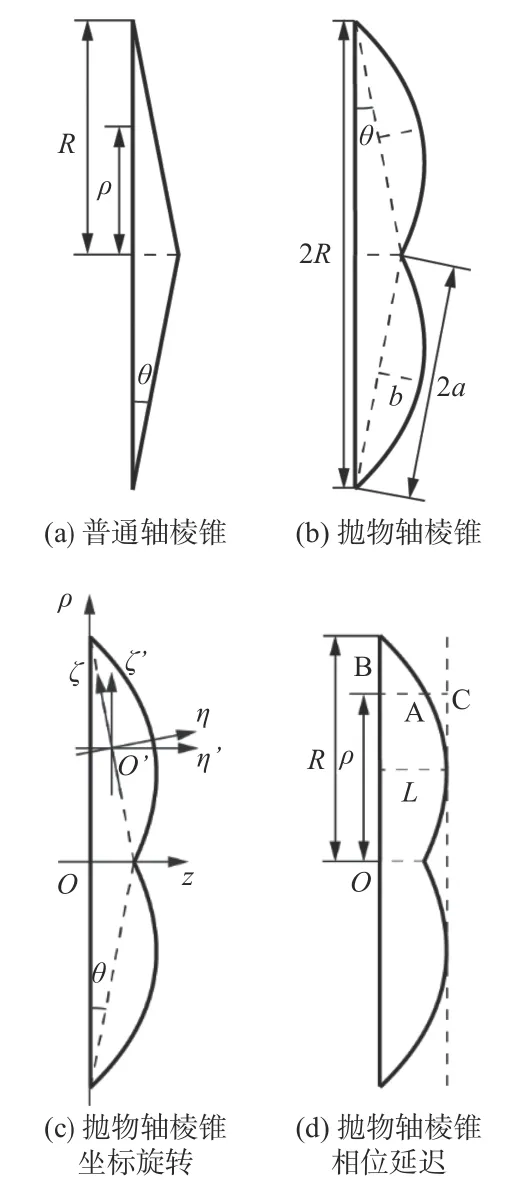
图1 棱锥结构示意图Fig.1 Structure diagram of pyramid

将光学元件放置于频率0.1 THz、束腰半径ω0=26 mm的准直高斯波束的束腰处，高斯波束可表示成：Ein=exp(-ρ2/ω02)，其中 ρ=为柱坐标系下的极轴。将光学元件看作薄器件，不考虑吸收损耗，则出射面的光场可表示为

式中：j 为虚数单位；，Δφ为波束通过光学元件的相位延迟。如图1(a)所示，普通轴棱锥的相位延迟为

式中：K=2π/λ表示波矢；n为材料折射率。

接下来计算抛物轴棱锥的相位延迟。如图1(c)所示，通过坐标系旋转和平移，将ξ-η坐标系转化为ρ-z坐标系。由于抛物轴棱锥是轴对称的，在此仅以z轴上半部分为例。ξ-η坐标系逆时针旋转θ后得到ξ’-η’坐标系：

ξ’-η’坐标系通过平移转换为ρ-z坐标系，可表示为

将公式(3)带入公式(4)，整理可得ξ-η坐标系转化为ρ-z坐标系的转换公式：

抛物线在ξ-η坐标系中的表达式为η=(-b/a2)ξ2+b，设A 点为抛物线上一动点，在ρ-z和ξ-η坐标系中的坐标分别为 (ρA,zA) 和 (ξA,ηA)。与ρ轴垂直，与ρ轴相交于B 点，在ρ-z和ξ-η坐标系中的坐标分别为 (ρB,zB)和 (ξB,ηB)。所以抛物轴棱锥的厚度函数为

将公式(5)带入公式（6），可得：

根据抛物线参数方程 ξ=(a2/b)tanα 和η=(-a2/b)tan2α+b，抛物轴棱锥的厚度函数可表示为

式中：参数 α∈[0,arctan(b/a)]∪[(π-arctan(b/a)),π]。对α求导，即：

当α满足公式(10)时，=0，取最大值，即：

如图1(d)所示，设L=且L=，抛物轴棱锥右侧的竖直虚线为出射面，则抛物轴棱锥的相位延迟为

式中：K=2π/λ表示波矢；n为材料折射率。在此仅考虑相对的相位延迟，将公式(12)的上下两式同时减去KL，再将公式(8)代入可得：

根据抛物轴棱锥的几何结构可知，a=R/2cosθ，k=a/b，代入（13）式可得：

式中 α∈[0,arctan(1/k)]∪[π-arctan(1/k),π]。因此，当抛物轴棱锥的底边 2R和底角θ确定后，k值是改变抛物轴棱锥相位延迟的唯一变量。

将公式(2)和公式(14)代入公式(1)，即可计算出普通轴棱锥和抛物轴棱锥的出射波束。两种光学元件的底边 2R=76.2 mm（3 in），底角 θ=10°。光学元件利用3D 打印技术制作，当频率为0.1 THz时3D 打印材料的折射率n为1.645。

利用角谱理论计算的仿真结果如图2 所示。图2(a)为利用公式(2)和公式(14)计算出的普通轴棱锥和抛物轴棱锥的相位分布；图2(b)为普通轴棱锥和抛物轴棱锥的出射波束在x-z面的光强分布。其中z=0对应光学元件的出射面，红色曲线为在x=y=0时在z方向的光强变化，称其为中心光强曲线。由图2(b1)可知，普通轴棱锥产生的无衍射波束紧贴元件，由图2(b2)～图2(b4)可知，抛物轴棱锥的出射波束从圆环状波束逐渐转变为由一个主瓣和多个旁瓣组成的无衍射波束，即无衍射波束与元件具有一定的距离。随着k值的增大，抛物轴棱锥的无衍射波束中的旁瓣数量逐渐减少，能量逐渐被聚集在中心主瓣。在此，类比于透镜中焦距的定义，将抛物轴棱锥的出射面与中心光强曲线最大值处之间的距离定义为“焦距”，因此，k=2，k=3和k=5时抛物轴棱锥的焦距分别为58 mm，88 mm 和129 mm。

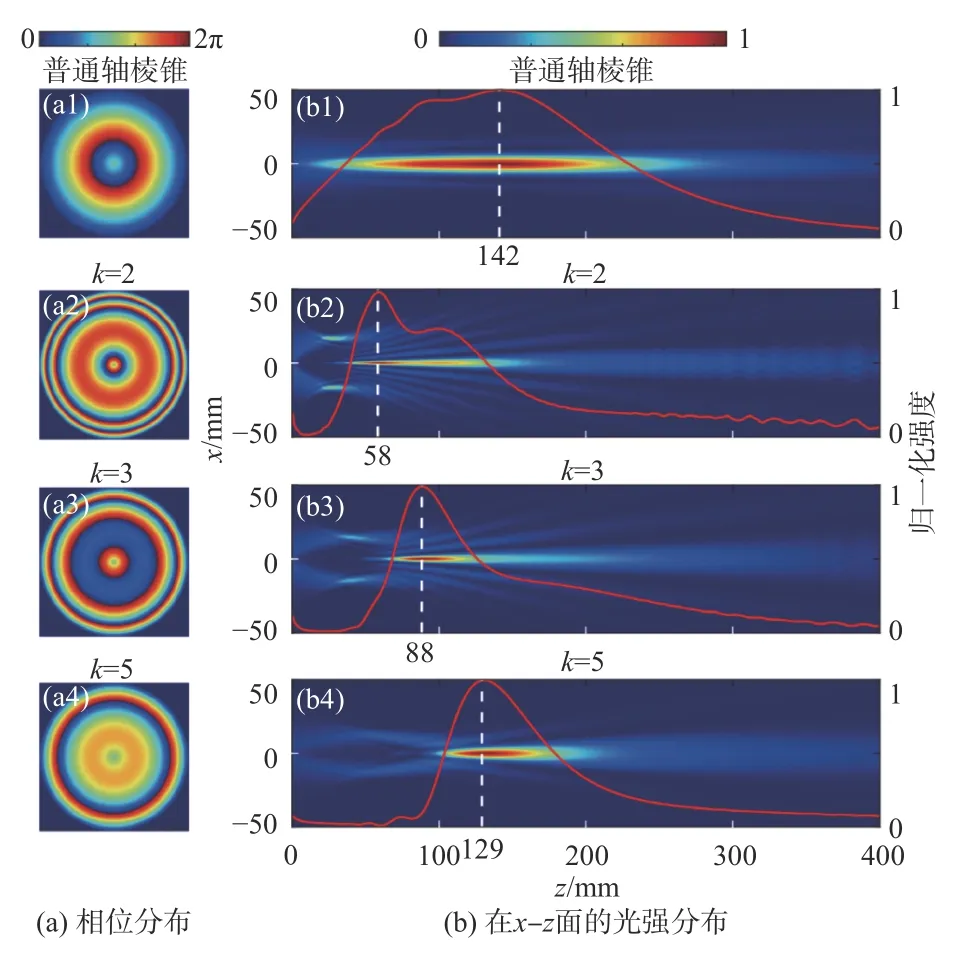
图2 普通轴棱锥和抛物轴棱锥的仿真结果Fig.2 Simulation results of normal axial pyramid and parabolic pyramid

2 频谱分析和实验验证

利用空间频谱进一步分析抛物轴棱锥产生的无衍射波束。普通轴棱锥和抛物轴棱锥都是中心对称的，所以其空间频谱也具有中心对称性，仅需观察空间频谱沿fρ方向的分布即可，如图3 所示。由图3 可知，相比于普通轴棱锥的圆环状空频，抛物轴棱锥的空间频谱是由一个幅值最大的主频和以原点为圆心、幅值逐渐降低的侧边频构成。因此，抛物轴棱锥产生的波束并不是普通轴棱锥产生的贝塞尔波束，而是一种新型的无衍射波束，根据抛物轴棱锥的空频形状，将其所产生的波束命名为“梳状空频无衍射波束”。

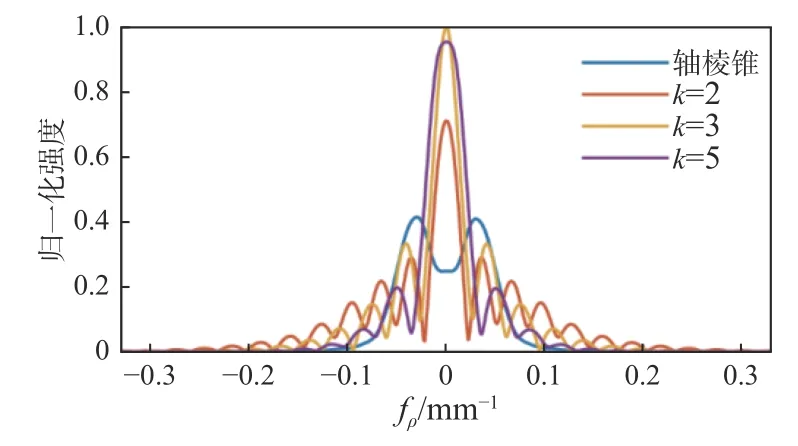
图3 普通轴棱锥和 k=2、3、5 时抛物轴棱锥的空间频谱Fig.3 Spatial frequency spectrum of normal axis pyramid and parabolic pyramid when k=2,3,5

以上仅为仿真计算和频谱分析结果，下面用实验验证抛物轴棱锥的波束行为。图4(a)为实验装置示意图，太赫兹源为单频耿氏二极管（SPACEK LABS,GW-900），频率为0.1 THz，功率为25 mW。使用一个直径76.2 mm、焦距100 mm 的透镜（高密度聚乙烯材料）对太赫兹源发射的发散波束进行准直，准直后高斯波束的束腰半径为26 mm。抛物轴棱锥利用3D 打印技术制作，打印精度为0.01 mm，打印材料为LY1101，该材料在0.1 THz 频率下的折射率和吸收系数分别为1.645 和1.2 cm-1。选择底角 θ=10°，底边 2R=76.2 mm，k=2、k=3的抛物轴棱锥进行制作，图4(b)为抛物轴棱锥的三维模型图和实物图。太赫兹探测器为肖特基二极管，将其固定在三维步进电机上进行单点逐行扫描。

图4 实验验证Fig.4 Experimental verification

抛物轴棱锥的实验结果如图5 所示。由于仿真空间的有限性，实验结果与仿真计算结果存在一定的差别，但出射波束的光强分布仍吻合较好。图5（a）和图5（b）分别为k=2 和k=3时抛物轴棱锥的光强分布。图5 中z=0对应抛物轴棱锥的出射面，红色曲线为中心光强曲线。由图5 可知，抛物轴棱锥产生的梳状空频无衍射波束与出射面具有一定的距离。以k=2的抛物轴棱锥为例，出射波束的起始阶段呈空心圆环状，中心光强在z=42 mm处取极小值，之后圆环状波束逐渐转变为由一个中心主瓣和多个旁瓣组成的无衍射波束，中心主瓣沿传播方向逐渐扩展，如图5(a)所示。由图5 可知，k=2 和k=3时抛物轴棱锥的焦距分别为154 mm和172 mm。在利用角谱理论进行计算时，将抛物轴棱锥看做薄器件，不考虑其吸收损耗，但实验中抛物轴棱锥具有一定厚度且存在能量吸收，因此，对于抛物轴棱锥的焦距，仿真结果与实验结果存在一定误差。

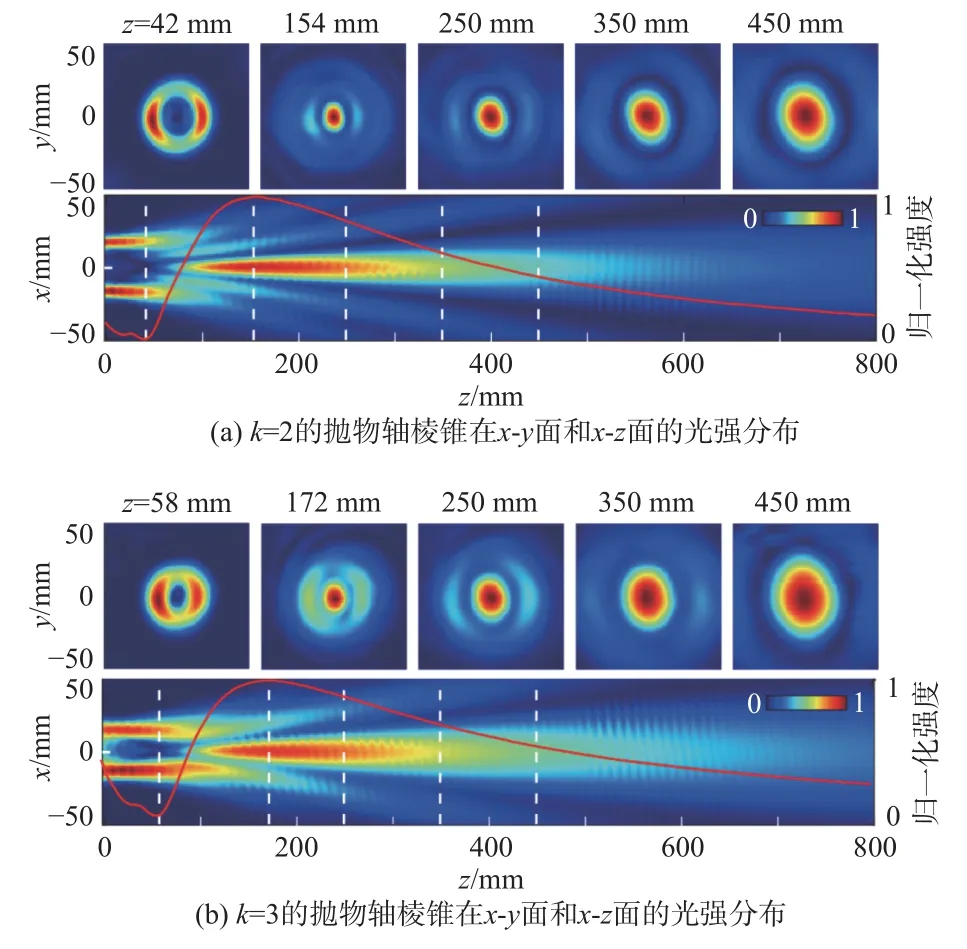
图5 抛物轴棱锥实验结果Fig.5 Experimental results of parabolic pyramid

3 结论

通过改变普通轴棱锥的几何结构，设计了一种新型的光学元件——抛物轴棱锥。该元件可以产生具有“焦距”的无衍射波束，在0.1 THz 频率下利用3D 打印技术制备了不同结构参数的抛物轴棱锥。仿真计算与实验结果均表明，抛物轴棱锥产生的无衍射波束与元件具有一定的距离。根据空间频谱，发现抛物轴棱锥产生了一种新型的无衍射波束，称其为“梳状空频无衍射波束”。这种利用抛物轴棱锥产生的“梳状空频无衍射波束”可应用于太赫兹成像领域，用于扩大成像系统的景深。