非完美CSI下的全双工中继网络的能效谱效均衡
2024-02-18张茜仇润鹤
张茜 仇润鹤
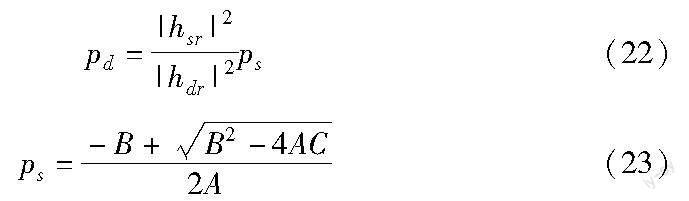
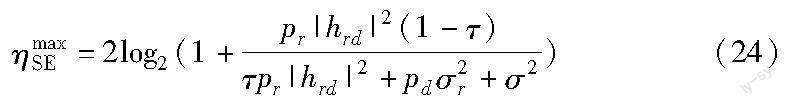
摘 要:为优化非完美信道状态信息下的解码转发全双工中继网络的能效和谱效,提出了一种基于该网络模型的能效谱效均衡策略。通过构建能量效率和频谱效率的折中优化函数,将一个非凸的多目标优化问题转换为一个凸的单目标优化问题,利用求导法和拉格朗日乘子法求解在不同折中因子下的最优中继发射功率。仿真结果表明,可以通过改变折中因子来优化系统的能效和谱效值,获得最优能效和谱效的性能折中。
关键词:非完美信道状态信息;全双工;能量效率;频谱效率;性能折中
中图分类号:TN925 文献标志码:A 文章编号:1001-3695(2024)01-038-0242-06
doi:10.19734/j.issn.1001-3695.2023.05.0205
Trade-off between energy efficiency and spectrum efficiency for full-duplex relay network with imperfect CSI
Abstract:In order to optimize the energy efficiency and spectral efficiency of decoded-and-forwarded full-duplex relay network in imperfect channel state information,this paper proposed an energy efficiency and spectral efficiency balancing strategy based on this network model.It could replace the non-convex multi-objective optimization problem to a convex single-objective optimization problem by constructing a compromise optimization function of energy efficiency and spectral efficiency.It used derivation method and Lagrange multiplier method to solve the optimal relay transmission power under different compromise factors.The simulation results show that changing the compromise factor can change the energy efficiency and spectral effectiveness of the system and obtain the performance tradeoff of energy efficiency and spectrum effectiveness.
Key words:imperfect channel state information;full-duplex;energy efficiency;spectrum efficiency;performance tradeoff
0 引言
傳统的通信系统和网络在发展和运营过程中会消耗大量的能量,同时产生大量的温室气体。此外,随着科技的发展,通信系统和通信网络的规模在不断扩大,将会导致更多的频谱需求,而频谱是不可再生资源,频谱短缺将会限制信息网络的发展。因此,如何减小通信网络的能量消耗和提高网络频谱的利用率成为近年来的研究热点。协作通信技术作为绿色节能通信中的关键技术,可以有效地解决无线信道衰退的缺点,被广泛应用于无线通信系统和网络中。在全双工通信中,通信双方可以同时发送和接收数据,宽带利用率高且传输时延少,已被广泛地应用到无线通信领域。但在实际应用中,完美信道状态信息的场景通常不存在,本文针对非完美信道状态信息下的全双工中继网络的能量效率和频谱效率均衡进行了研究。将上述非完美信道状态信息下的全双工中继网络引入到D2D通信场景中,可以扩大D2D的通信范围,获得更好的通信网络性能,可以减小网络功耗、缓解基站负载压力以及提升网络频谱效率[1]。因此,引入非完美信道状态信息下的全双工中继网络的D2D已成为第五代移动通信网络的研究热点。文献[2]提出了一个全双工双向无线携能(simultaneous wireless information and power transfer,SWIPT)中继系统模型,该模型在非完美信道状态信息(channel state information,CSI)下,在中继节点处引入SWIPT技术,有效提高了系统的能量效率。文献[3]研究了下行非正交多址异构网络,在考虑不完全信道状态信息下网络的能效优化问题,通过基于梯度值的二分搜索算法实现各单元的功率分配,仿真结果表明,所提算法相比传统算法能够显著提高能量效率。文献[4]研究了基于衰落信道的无线信息与SWIPT技术的物联网分布式天线系统的能效优化问题,提出了基于不完全信道状态信息的资源分配方案,计算仿真结果表明,所提方案能以较低的复杂度获得较好的能量效率。文献[5,6]研究了非完美CSI下的大规模多输入多输出系统的能量效率优化问题 。文献[7]研究了不完全CSI全双工系统的EE问题,提出了一种基于范数的联合天线和用户选择算法,通过使用禁忌搜索来选择最优的天线和传输用户,并利用拉格朗日对偶分解方法,推导出在各个单元中独立运行的功率分配策略,仿真结果表明,该算法可以在多次迭代中获得最大的EE。文献[8]在考虑了不完全CSI、收发器硬件噪声和RSI的情形下,通过调整源节点和中继节点的传输功率,可以节约系统能耗且多天线全双工系统也可以获得更好的系统性能。文献[9]研究了一种多输入多输出系统,针对CSI未知、能量效率低、传输体积需求繁多等问题,提出了一种分布式迭代算法来优化求解公式问题,仿真结果表明,所提方案可以达到最优的能量效率。文献[10]在不完全CSI的多用户多基站NOMA-MEC网络中,通过优化任务分配、功率分配和用户关联来降低网的能耗。上述文献[2~10]只研究了非完美CSI下系统的能量效率,并未对频谱效率进行研究。
文献[11]研究了认知无线电网络的性能,在非完美CSI和SIC的影响下进行预测,最后通过仿真实验验证了所提系统的中断概率和频谱效率更有优势。文献[12]提出了一种不完全CSI下的非线性波形非正交多址系统,研究在完全和不完全CSI下系统的吞吐量。文献[13]针对频分双工多用户大规模MIMO系统提出了一种改进的CSI采集方案,采用波束形成的信道状态信息参考信号传输机制,仿真结果表明,所提方案可以获得更高的SE性能。文献[14]研究了非正交多址双跳中继辅助网络中部分中继选择的性能,在不完美CSI下,通过推导中断概率的闭合表达式获得了网络的遍历容量和吞吐量。文献[15] 针对在不完全CSI下使用非正交多址(non-orthogonal multiple access,NOMA)增强合作中继系统的性能降低的问题提出了一种不完全CSI下D2D辅助协作NOMA通信的功率分配算法。文献[11~15]只研究了非完美CSI下系统的频谱效率,但并未对系统的能量效率进行研究。文献[16]研究了全双工中继系统在不同中继方案下的系統能量效率和频谱效率之间的关系。文献[17]研究了放大转发全双工双向中继网络的能量效率和频谱效率的均衡问题,仿真结果表明,该网络比半双工中继网络具有较高的SE和较低的EE。文献[18]研究了智能优化对大规模MIMO系统的频谱效率-能量效率优化的最优值问题,实验结果表明多目标萤火虫算法的结果比多目标差分进化算法和多目标粒子群优化算法结果更好。文献[19]利用发射天线和发射功率的一阶导数,研究了下行大规模MIMO系统中EE和SE之间的权衡问题。文献[16~19]在完美信道状态信息下研究了能量效率和频谱效率的均衡问题,并未对非完美信道状态信息下的能效和谱效进行研究。
综上所述,由于全双工中继网络的能量效率和频谱效率相矛盾,无法同时求得最优能效和最优谱效,所以研究非完美信道状态信息下全双工中继网络的能量效率和频谱效率均衡具有重要意义。本文在考虑非完美信道状态信息下提出了一种基于解码转发的全双工中继网络的EE和SE的均衡策略。首先,在考虑非完美信道状态信息的条件下,通过定义信道估计误差因子推导出在非完美信道状态下的能量效率和频谱效率的表达式,通过引入折中因子构造一个能量效率和频谱效率的优化函数,将一个非凸的多目标能效最大化问题和谱效最大化问题转换为一个凸的单目标能效和谱效均衡的优化问题,利用求导法和拉格朗日乘子法求解在不同均衡因子下的最优中继发射功率。
1 系统模型
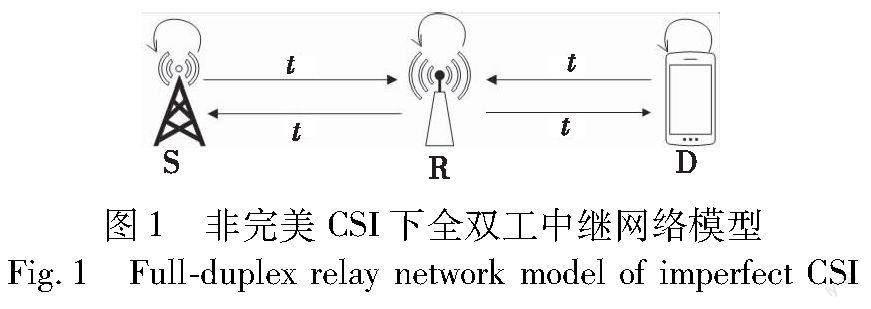
本文解码转发全双工中继网络模型由源节点、中继节点和目的节点组成,为便于表示,源节点记为S,中继节点记为R,目的节点记为D,如图1所示。
本文模型中的所有节点均处于全双工模式,采用DF协议进行传输,且不考虑直传链路。节点处于全双工双向模式,所以信号传输在一个时隙内就可以完成,即源节点和目的节点同时将信息发送给中继节点,中继节点接收到信息后进行解码再编码后分别转发给目的节点和源节点。信道服从瑞利衰落,信道衰落系数为hij(i,j∈s,r,d),所有中继均处于全双工模式,因此会存在自干扰,|hii|2为自干扰消除后残余自干扰增益,令其满足hii~CN(0,σ2R)。为便于理解,表1给出了变量符号的相关含义。
在t时隙,源节点、中继节点和目的节点接收到的信号分别为
其中:pi为节点的传输功率;xi为节点的发送信号,满足E{|xi|2}=1;ni为节点的加性高斯白噪声,满足ns,nr,nd~CN(0,σ2)。由于信道处于非完美CSI下,需要考虑信道估计误差,由文献[20]可知实际信道增益与估计值之间的关系为
其中:h^ij为实际信道增益的估计值;eij为实际的信道估计误差。假设实际信道增益和信道估计误差相互独立,且估计误差服从eij~CN(0,σ2ij)。假设所有节点的信道估计能量相同,定义信道估计误差因子τ=e2ij/|hij|2,因此可得到实际信道增益的估计值为
|h^ij|2=|hij|2-σ2ij=(1-τ)|hij|2(5)
将式(4)代入式(1)~(3)中可得
根据文献[21]可知全双工双向中继网络的实际可达的传输速率为
上行链路的实际数据传输速率为
RSD=min{Csr,Crd}(13)
下行链路的实际数据传输速率为
RDS=min{Cdr,Crs}(14)
假设带宽为单位带宽,则非完美CSI下全双工中继网络的频谱效率ηSE可表示为
ηSE=RSD+RDS(15)
2 非完美CSI下FD中继网络EE和SE均衡
2.1 EE和SE最优化
非完美CSI下全双工中继网络的总功率消耗包括非理想放大功率消耗和电路功率消耗,非理想放大功率消耗采用传统功率放大模型[22],即ΦTPA=εpt,其中,ε为非理想功率放大因子,pt为发射功率可表示为pt=ps+pr+pd;电路功率消耗主要包括混频器功率消耗pmix,频率合成器功率消耗psyn,数模转换器功率消耗pDAC,编码器功耗pecc。因此非完美CSI下FD中继网络的总功率PT为
PT=εpt+pc(16)
其中:电路功率pc=pmix+psyn+pDAC+pecc。
在非完美CSI下全双工中继网络模式的能量效率被定义为频谱效率和总功率的比值,可以表示为
若使解码转发全双工中继网络的频谱效率达到最大,需要使下列等式成立:
将式(5)代入式(18)(19)中可得
当RSD=RDS时,可得
其中:A=(2-2τ-3τ2)|hsr|4σ2R
B=(2-2τ-3τ2)|hsr|2|hdr|2σ2-(2τ3+τ2)|hsr|2|hrd|4pr-
(1+2τ)σ2σ2R|hsr|2-(1+2τ)prσ4R|hsr|4
C=(prσ2R+σ2)[-(1+τ2)pr|hrd|4-(1+2τ)σ2|hdr|2]
非完美CSI下FD中继网络的频谱效率可达到最优,即
当非完美CSI网络的频谱效率达到最优时,系统的能量效率可以表示为
为了最大化非完美CSI网络的能量效率,建立能量效率最优化模型,该模型以中继发射功率为优化变量,此时系统的最大能量效率可表示为
由上述约束条件可得pr的取值范围,即pr∈[0,pmaxr],在该范围内,ηEE对pr求导可得
其中:
由于上式ψ(pr)>0,所以对分子(pr)求导可得
因此,存在一个最优的p*r使得ηEE(pr)在[0,p*r)单调递增,在(p*r,+∞)单调递减。当pr=p*r时,系统的能量效率ηEE(pr)可达到最大。但是,由于(pr)为超越方程,无法通过正常算术运算求解,所以需要利用标准的凸优化工具求解。
由式(26)可构造拉格朗日函数,可得函数表达式为
其中:λ1≥0和λ2≥0为上述不等式的约束系数,通过KKT条件可得
通過KKT条件可以算出pr的最优值为p*r,即可得到非完美CSI下全双工中继系统的能效最大值。
2.2 EE和SE的均衡
为最大化非完美CSI全双工中继网络的EE和SE,建立了一个多目标优化问题P1:
随着pr的增大,SE逐渐增大,而EE逐渐减小,导致EE和SE相矛盾,最大化功率不相同。为了解决这一问题,引入帕累托最优集,得到目标函数的帕累托最优集为
从上述的帕累托最优集中可以看出,当p*r≥pmaxr时,多目标优化问题P1的全局最优解是唯一的pmaxr,因此本文仅需要考虑0 其中:ηmaxEE和ηmaxSE分别表示非完美CSI下全双工中继网络的EE和SE的最大值,可表示为 ηmaxEE=ηEE(p*r)(35) ηmaxSE=ηSE(pmaxr)(36) 利用加权标量法,定义一个折中因子δ∈[0,1],将EE和SE表达式串联起来,可得到一个新的变量EE-SE,定义为 ξEE-SE(pr)=[ξSE(pr)]δ[ξEE(pr)]1-δ(37) 从式(37)可以看出,ξEE-SE(pr)随着δ的变化而变化,当δ→0时,ξEE-SE(pr)更偏向于EE;当δ→1时,ξEE-SE(pr)更偏向于SE。通过引入折中因子,将多目标优化问题P1转换为单目标优化问题P2: 由于式(37)计算较复杂,为简化计算,将式(37)转换为 H(pr ) = log2 ξEE-SE(pr)= δlog2 ξSE (pr)+(1-δ)log2ξEE(pr)(39) 将式(35)(36)代入式(39)中可得 H(pr)=log2ηSE(pr)-(1-δ)log2PT(pr)- [δlog2ηmaxSE+(1-δ)log2ηmaxEE](40) 对H(pr)求一阶导数可得 θ(pr)和ω(pr)分别表示为 根据式(44)可知,有且仅有一个p*r,使得H(pr)存在极值,当pr∈[p*r,p**r)时,H(pr)/pr<0;当pr∈[p**r,pmaxr)时,H(pr)/pr>0。所以,H(pr)在pr∈[p*r,pmaxr]为严格的凹函数。当H(pr)/pr=0时,令α(pr)=1-δ,即可得到 因此,求解pr关于δ的单调性可转换为pr关于α(pr)的单调性,α(pr)对pr求一阶导数可得α(pr)/pr<0,可以通过导数的正负来判断α(pr)的单调性,即α(pr)关于pr严格递减,所以δ关于pr为严格增函数,由定理可知单调递增函数的反函数也为单调递增函数,因此,pr关于δ也为严格递增函数。因为H(pr)导数的分母恒大于零,分子θ(pr)对pr求一阶导数可得 通过式(46)可以看出,δ的取值会影响H(pr)的结果,因此,为求解H(pr)的最大值,可分以下几种情况进行说明。 1)当δ=0时 将δ=0代入式(46)中可得 此时,对比式(28)与(47)可以看出(pr)/pr=θ(pr)/pr≤0,由此可以得出,在[p*r,pmaxr],ξEE-SE(pr)单调递减,因此当pr=p*r时,ξEE-SE(pr)最大。 2)当δ=1时 将δ=1代入式(46)可得 3)当0<δ<1时 可以发现EE和SE均与δ有关,可以通过设置不同的δ值时使得EE和SE的系统性能最佳。 综上分析,定义中继最优发射总功率为poptr(pr)∈Ω,此时P2的帕累托最优集为 因此,EE和SE均衡的方法流程如下:a)通过求导法和拉格朗日乘子法求得SE和EE的最优中继功率pmaxr和p*r;b)由于SE和EE相互矛盾,所以引入帕累托最优集Ω;c)通过归一化和加权标量法引入折中因子δ,获得EE-SE均衡函数;d)通过求解均衡函数,分析在不同δ下的EE和SE。 3 仿真结果与分析 本文利用MATLAB软件进行仿真分析,在非完美CSI全双工中继网络中,通过归一化源节点和目的节点间的距离,并设置各相关参数,如表2所示。对比不同中继距离和不同折中因子等因素下EE和SE的性能。 图2所示为完美CSI和非完美CSI下全双工中继网络的EE与平均信噪比的关系,分别设置残余自干扰的功率为0.05 W和0.4 W,对于完美CSI,信道估计误差通常设置为零,且忽略信道估计误差消耗的功率;对于非完美CSI的情况,设置信道估计误差的方差σ2esr=σ2erd=σ2err=0.05。由图2可以看出,完美CSI下的EE优于非完美CSI下的EE,在相同信道估计误差下,残余自干扰越大,全双工中继网络的EE越小;同时EE随着SNR的增大呈现先增大后减少的趋势,在SNR较低的范围内,完美CSI和非完美CSI 的差距较小,但随着SNR的增大,完美CSI 和非完美CSI的差距逐渐增大。图3为完美CSI和非完美CSI下全双工中继网络的SE与平均信噪比的关系,分别设置残余自干扰的功率为0.05 W和0.4 W,对于完美CSI,信道估计误差通常设置为零,且忽略信道估计误差消耗的功率;对于非完美CSI的情况,设置信道估计误差的方差σ2esr=σ2erd=σ2err=0.05。由图3可以看出,完美CSI下的SE优于非完美CSI下的SE,在相同信道估计误差下,残余自干扰越大,全双工中继网络的SE越小。从图中可以看出,SE随着SNR的增大而增大。 图4和5所示分别为非完美CSI下全双工中继网络在不同信道估计误差下的EE和非完美CSI下全双工中继网络在不同信道估计误差下的SE。从图中可以看出EE随着SNR的增大呈现先增大后减小的趋势,SE随着SNR的增大呈现增大的趋势。同时还可以看出,信道估计误差越小,非完美CSI下的全双工中继网络的EE和SE越大,且随着平均SNR的增大,不同信道估计误差之间的差距也越来越大。 功率为poptr;当δ=0时,最优发射功率为poptr=p*r;当δ=1时,最优发射功率为poptr=pmaxr;当0<δ<1时,最优发射功率为poptr=p**r,与理论分析的帕累托最优集一致。此外,从图8还可以看出,最优发射功率随着折中因子δ的增大而增大,这与式(45)中的分析pr关于δ为严格增函数相一致。 4 结束语 本文研究了非完美CSI下全双工中继网络的EE和SE的均衡,在非完美CSI下,解码转发全双工中继网络需要对信道进2行信道估计。本文针对不同信道估计误差下全双工中继网络的EE和SE进行研究,解决了在非完美CSI下的全双工中继网络的EE和SE优化问题,采用求导法和拉格朗日乘子法求解中继最优发射功率,进而求出最优能效和最优谱效。仿真实验验证了所提方法可以通过改变折中因子优化系统的EE和SE,且折中因子位于0.47附近时可以得到SE=EE=H,实现EE和SE的均衡,可以获得中继网络的最优能效谱效的性能折中。本文采用的系统模型不适用于多用户和多中继系统等,下一步将研究多用户和多天线中继系统的EE和SE的均衡。 参考文献: [1]Selmi S,Bouallègue R.Joint spectral and energy efficient multi-hop D2D communication underlay 5G networks[C]//Proc of International Conference on Software,Telecommunications and Computer Networks.Piscataway,NJ:IEEE Press,2020:1-6. [2]王令照,仇润鹤.解码转发双向无线携能全双工中继系统的能效研究[J].信号处理,2022,38(4):806-815.(Wang Lingzhao,Qiu Runhe.Energy efficiency research of decode-and-forward two-way simultaneous wireless information and power transfer full-duplex relay system[J].Journal of Signal Processing,2022,38(4):806-815.) [3]Song Xin,Dong Li,Wang Jingpu,et al.Energy efficient power allocation for downlink NOMA heterogeneous networks with imperfect CSI[J].IEEE Access,2019,7:39329-39340. [4]Yu Xiangbin,Chu Junya,YuKai,et al.Energy-efficiency optimization for IoT-distributed antenna systems with SWIPT over composite fading channels[J].IEEE Internet of Things Journal,2020,7(1):197-207. [5]張逸凡,陈显哲,彭张节.非完美CSI下大规模MIMO DF中继多用户对全双工通信系统性能研究[J].上海师范大学学报:自然科学版,2022,51(2):149-156.(Zhang Yifan,Chen Xianzhe,Peng Zhangjie.Research on the performance of massive MIMO DF relay multi-pair full-duplex communication system under imperfect CSI[J].Journal of Shanghai Normal University:Natural Sciences,2022,51(2):149-156.) [6]禹永植,张春红,郝海.非完美CSI情况下大规模MIMO系统的下行链路能效优化[J].系统工程与电子技术,2022,44(5):1694-1700.(Yu Yongzhi,Zhang Chunhong,Hao Hai.Downlink energy efficiency optimization for massive MIMO systems with imperfect CSI[J].Systems Engineering and Electronics,2022,44(5):1694-1700.) [7]Alemayehu T S,Yoon W.Joint optimal resource allocation in energy-efficient multicell large-scale distributed full-duplex antenna system with imperfect CSI[J].Wireless Personal Communications,2021,123(3):85-102. [8]Nguyen B C,Dung L T,Hoang T M,et al.Impacts of imperfect CSI and transceiver hardware noise on the performance of full-duplex DF relay system with multi-antenna terminals over Nakagami-m fading channels[J].IEEE Trans on Communications,2021,69(10):7094-7107. [9]Wang Shiqi,Ma Lin,Wang Xuedong.Optimization of energy efficiency for uplink wireless information and downlink power transfer system with imperfect CSI[J].Wireless Communications & Mobile Computing,2021,2021:article ID 9990893. [10]Fang Fang,Wang Kaidi,Ding Zhiguo,et al.Energy-efficient resource allocation for NOMA-MEC networks with imperfect CSI[J].IEEE Trans on Communications,2021,69(5):3436-3449. [11]Do D T,Le T A,Nguyen T N,et al.Joint impacts of imperfect CSI and imperfect SIC in cognitive radio-assisted NOMA-V2X communications[J].IEEE Access,2020,8:128629-128645. [12]李赛,党小宇,虞湘宾,等.不完全信道状态信息下非线性波形非正交多址接入系统吞吐量分析[J].电子与信息学报,2022,44(8):2749-2756.(Li Sai,Dang Xiaoyu,Yu Xiangbin,et al.Throughput analysis of non-linear waveform non-orthogonal multiple access system with imperfect channel state information[J].Journal of Electronics & Information Technology,2022,44(8):2749-2756.) [13]Zhang Fangchao,Sun Shaohui,Gao Qiubin,et al.Enhanced CSI acquisition for FDD multi-user massive MIMO systems[J].IEEE Access,2018,6:23034-23042. [14]Mondal S,Roy S D,Kundu S.Partial relay selection in energy harvesting based NOMA network with imperfect CSI[J].Wireless Personal Communications,2021,120(4):3153-3169. [15]Wang Jingpu,Song Xin,Dong Li,et al.Power allocation for D2D aided cooperative NOMA system with imperfect CSI[J].Wireless Networks,2021:1-14. [16]Chen Zhengchuan,Quek T Q S,Liang Yingchang.Spectral efficiency and relay energy efficiency of full-duplex relay channel[J].IEEE Trans on Wireless Communications,2017,16(5):3162-3175. [17]Chen Hongbin,Li Gang,Cai Jun.Spectral-energy efficiency tradeoff in full-duplex two-way relay networks[J].IEEE Systems Journal,2018,12(1):583-592. [18]Gül B K,Tapinar N.Usage of intelligent optimization techniques for estimation of pareto optimal front of spectral efficiency-energy efficiency trade-off in massive MIMO systems[C]//Proc of Palestinian International Conference on Information and Communication Technology.Piscataway,NJ:IEEE Press,2021:152-156. [19]Salh A,Audah L,Abdullah Q,et al.Trade-off energy and spectral efficiency with multi-objective optimization problem in 5G massive MIMO system[C]// Proc of the 1st International Conference on Emerging Smart Technologies and Applications.Piscataway,NJ:IEEE Press,2021:1-6. [20]林家玉.非完美CSI下認知双向中继系统的鲁棒功率分配[D].西安:西安电子科技大学,2015.(Lin Jiayu.Robust power allocation for cognitive two-way relay systems under imperfect CSI[D].Xian:Xidian University,2015.) [21]Nam W,Chung S Y,Lee Y H.Capacity of the Gaussian two-way relay channel to within 1/2 bit[J].IEEE Trans on Information Theory,2010,56(11):5488-5494. [22]Cui Qimei,Zhang Yuhao,Ni Wei,et al.Energy efficiency maximization of full-duplex two-way relay with non-ideal power amplifiers and non-negligible circuit power[J].IEEE Trans on Wireless Communications,2017,16(9):6264-6278.
