自适应状态转移模拟退火算法及其应用

徐博 韩晓霞 董颖超 卢佳振 武晋德 张文杰

摘 要：状态转移模拟退火算法（STASA）作为解决复杂优化问题的有效方法，其搜索效率依赖于搜索算子和参数值的选择，在一些高维复杂问题上出现效率低下的问题。提出一种自适应状态转移模拟退火算法（ASTSA），通过自适应算子和参数选择策略来提高算法的适用性和求解效率；借鉴群智能算法的均值更新方法对平移算子进行改进，增强算子的搜索特性。通过23个基准测试函数和8个工程设计问题进行实验验证并与其他算法对比，证明了ASTSA算法和改进策略的有效性。

关键词：状态转移模拟退火算法；自适应策略；连续优化问题；工程设计问题

中图分类号：TP301.6   文献标志码：A   文章编号：1001-3695（2024）01-022-0150-09

doi：10.19734/j.issn.1001-3695.2023.06.0221

Adaptive state transition simulated annealing algorithm and its application

Abstract：State transition simulated annealing（STASA） algorithm has achieved outstanding results in solving complex optimization problems.However，its search efficiency depends on the selection of search operators and parameter values，resulting in low efficiency in some high-dimensional complex problems.This paper proposed an adaptive state transition simulated annealing（STASA） algorithm by introducing adaptive operators and parameter selection strategies to improve the applicability and efficiency of the algorithm.And it improved the translation operator by referring the mean update method of swarm intelligence algorithms to enhance the search characteristics of operator.This paper demonstrates the effectiveness of ASTSA and the improved strategy through experimental validation with 23 benchmark test functions and 8 engineering design problems and comparision with other algorithms.

Key words：state transition simulated annealing algorithm；adaptation strategy；continuous optimization problem；enginee-ring design problem

智能优化算法又称为元启发式算法，起源于20世纪50年代的数值优化方法，随着算力的增强和人工智能的不断发展，逐渐发展为一种可以自动化地找到最优解的优化算法。智能优化算法具有高效、灵活、全局搜索等特性，可以有效地解决复杂的优化难题。近年来，随着数据科学和人工智能技术的快速发展，智能优化算法得到了极大的推广和应用，在工业生产、交通运输、资源配置等多个领域，智能优化算法已经成为解决优化问题的重要工具之一。

在智能优化算法的研究和发展中逐渐分为四类算法：a）基于自然进化的进化类算法，如遗传算法GA［1］、差分进化DE［2］等；b）基于生物种群的群智能算法，如粒子群算法PSO［3］、鲸鱼优化算法WOA［4］等；c）基于模拟各种物理现象的优化算法，如模拟退火算法SA［5］、引力搜索算法GSA［6］等；d）基于模拟人类智力、行为的優化算法，如帝国竞争算法ICA［7］、头脑风暴优化BSO［8］等。当然，它们的划分并非绝对的，如头脑风暴优化的灵感来源于人类的智力行为，但它同样属于群智能算法。

状态转移模拟退火（state transition si-mulated annealing，STASA）算法是Han等人提出的一种新的混合智能优化算法［9］，它结合了状态转移算法STA［10，11］和模拟退火算法SA的优点，已在PM 2.5浓度预测［12］、化学过程模型优化［13］、MTSP求解［14］等问题中取得了良好的应用。然而，STASA在求解大规模优化问题时出现收敛缓慢的问题，此外搜索算子的固定变换因子也限制了算法的收敛速度以及搜索效率，在搜索中对全局搜索和局部挖掘的划分不够明确，导致存在无效搜索。在STA中存在类似问题，Zhou等人［15］设计了一个参数集合来选择最优参数；进一步，董颖超等人［16，17］使用统计方法自适应调整算子及参数值。

本文针对STASA算法的不足对其进行改进，提出了一种自适应状态转移模拟退火算法（ASTSA）。在ASTSA算法中，通过统计方法引入自适应策略，根据算法的求解情况选择当前最佳的搜索算子及其对应的参数值；对平移算子进行改进，减少随机性，更好地反映优化问题的收敛方向，以发挥平移算子的搜索特性。最后将ASTSA在23个基准测试函数以及8个工程优化设计问题上进行实验，证明了其有效性。

1 状态转移模拟退火算法

STASA采用与STA相同的状态转移算子来生成候选解，并使用SA的Metropolis接受准则作为解的更新策略，提高跳出局部最优的能力。STA是一个基于现代控制理论中状态空间的相关概念的随机优化算法，STA使用状态空间代表优化算法的搜索空间，用“状态”表示优化问题的解，解的更新过程看作状态的转移过程［10］。因此，STA以及STASA生成候选解的统一形式可以使用控制转移方程表示为

其中：以xk、xk+1表示当前解和新一代解，yk为xk的适应度值，uk为当前状态与历史状态的记录；Ak，Bk∈RApn×n为随机矩阵；f（·）表示适应度函数。

1.1 状态变换算子

用于求解连续问题的STASA有四个状态转移算子，分别为旋转、平移、伸缩以及轴向变换算子，保证了全局搜索能力、局部开发能力以及启发式搜索能力。

a）旋转算子。

其中：εα>0为旋转因子；Rr∈RApn×n是［0，1］内服从均匀分布的随机矩阵；‖·‖2表示向量的二范数。旋转算子在以xk为球心、εα为半径的超球体内产生的候选解均。

b）平移算子。

其中：εβ>0为平移因子；Rt∈RAp为［0，1］内服从均匀分布的随机数；xk-1表示上一代解；平移变换表示xk沿着xk+1方向进行搜索。

c）伸缩算子。

xk+1=xk+εγRexk（4）

其中：εγ>0为伸缩因子；Re∈RApn×n为随机对角矩阵，服从标准高斯分布。伸缩算子具有全局搜索能力。

d）轴向变换算子。

xk+1=xk+εδRaxk（5）

其中：εδ>0为轴向变换因子；Rα∈RApn×n为随机稀疏对角矩阵，只有一个随机位置不为0，服从标准高斯分布。轴向变换算子可以增强单维搜索能力。

1.2 解的更新策略

STASA算法在原有贪婪策略中引入模拟退火算法SA的更新策略，即在新解更优时，按照贪婪策略直接接收更优解为当前解；而在新解非优时，按照Metropolis准则依概率接收新解。

在STASA中，使用状态变换算子产生的新候选解称为状态集合state，state中最优解记为bestk-1，因此该策略的数学表示为（以求解最小优化为例）

其中：Tk为当前模拟退火的温度；η为［0，1］内的随机数。当bestk+1优于xk时，e-（f（bestk+1）-f（xk））/Tk为大于1的值，一定接收新解；而非优时，则依概率接收bestk+1，否则保持xk为下一代解。

2 自适应状态转移模拟退火算法

算子是元启发式算法的重要组成和不同算法之间的主要区分，对待不同的优化问题，不同的算子能够产生不同的效果。为提高STASA算法的收敛速度、增强搜索能力，并提高算法对不同优化问题的适用性，将自适应策略引入STASA中并对平移算子进行改进。将这种自适应状态转移模拟退火算法记为ASTSA。

2.1 自适应调用策略

算子的周期性交替调用策略并不能完全发挥每个算子的搜索能力，导致部分计算资源不能得到充分的利用；此外，算子参数的选择也会显著地影响算子的优化性能。本文基于统计方法设计了一个自适应算子和参数选择策略，引入STASA。自适应调用策略基于统计方法设计了综合评价指标ρc，包括成功率ρs和下降率ρd两部分，定义如下：

其中：SE表示搜索强度；Best0表示算子调用前的旧最优解；fBest0表示Best0的适应度值；Ns为适应度值优于fBest0的解的个数；fave表示这Ns个解的平均适应度值。

平移算子只在伸缩、旋转和轴向变换三个算子发现更优解时调用，因此算子的自适应选择部分不包含平移算子，其调用规则并不改变。使用ρsE、ρsR、ρsA分别表示伸缩、旋转、轴向变换算子某次搜索的成功率，ρdE、ρdR、ρdA表示对应的下降率，则伸缩、旋转和轴向变换三个算子的综合评价指标ρcE、ρcR、ρcA计算方式如下：

其中：a1+a2=1，a1和a2为重要性系数，一般a1=a2=0.5。式（9）～（11）中，成功率ρs代表当前搜索中更优解所占的比例；下降率ρd反映当前搜索中更优解的平均收敛程度；综合评价指标ρc越大，表示该算子此次搜索的效果越好。

在自適应策略中分别计算三个算子的综合评价指标ρc，以确定最优算子，为了充分发挥最优算子的效果，确定算子后会重复调用Tp次。

参数的取值会显著地影响算子的搜索效果。在算法的自适应策略中，三个算子不再是使用固定的参数，而是设置一个参数集Ω，即在计算综合评价指标过程中，三个算子分别基于此参数集Ω中每个参数值进行搜索，并根据式（9）～（11）计算ρc，选择最优算子。

最优参数的选择与最优算子的选择在自适应策略中相互贯穿。在确定最优算子后，找到该算子在此次搜索中产生的最优解对应的参数，即确定为最优参数α*，数学表达为

其中：BestOp（）表示最优算子；f（·）表示适应度函数；xk表示当前解。

2.2 改进平移算子

平移算子在搜索过程中利用新最优解的方向信息，若当前解与新最优解的方向能够很好地反映优化问题的最优收敛方向，则平移算子能够专一地沿收敛方向进行搜索，搜索效率很高；若此方向与最优收敛方向存在偏差，搜索效率降低。在此借鉴群智能算法中使用种群均值进行辅助更新的思想，对平移算子的搜索方向进行改进。群智能算法在搜索过程中会使用种群内最优个体为产生下一代种群作参考，以求达到最优的搜索效果；也会使用次优个体［18， 19］、种群平均个体［20， 21］等信息以保证算法的稳定性，进而增强搜索效果。

改进后的平移算子以当前解为分界线，比当前解差的候选解记为xworse，优于当前解的候选解记为xbetter，使用xworse和xbetter的位置信息指示平移算子的搜索方向。改进平移算子的数学表达式为

其中：n1和n2分别为劣于、优于当前解的候选解的数量。其余与原平移算子相同。

改进平移算子的搜索方向不再单一地由新最优解确定，而是通过取均值的方式根据更劣解、更优解确定搜索方向。改进平移算子使用更优解的均值来代替单独的新最优解，减少了搜索方向的误差，并使用劣解的均值代替原平移算子中的当前解，辅助确定搜索方向。因为劣解的均值与当前解相比更能够反映优化问题的收敛方向，所以改進平移算子能够减少原平移算子单一最优解提高搜索方向带来的随机性，更准确地反映优化问题的最优收敛方向，以发挥平移算子的搜索特性。

图1为改进前后平移算子在搜索空间产生新候选解的示意图，背景为等高线图（圆心为全局最优），图中正方形表示原平移算子产生的候选解，三角形表示改进后平移算子产生的候选解，可以看到，沿三角形方向可以更快地接近全局最优。

2.3 算法整体框架

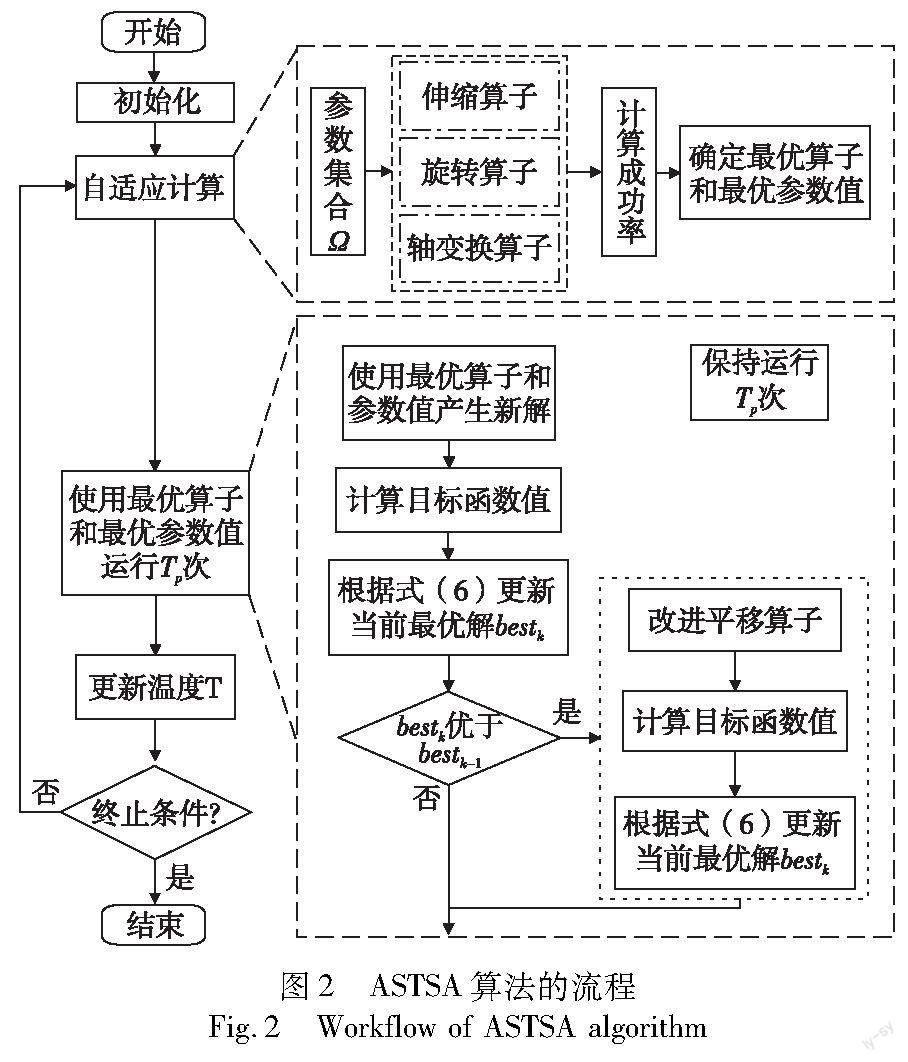
自适应状态转移模拟退火算法的流程如图2所示。在每次迭代中，首先使用自适应策略确定伸缩、旋转、轴变换算子的综合评价指标，以确定当前迭代的最优算子以及最佳参数值；为了充分发挥最优算子和参数值的优势，将其保持运行Tp次，并依据搜索情况调用改进平移算子，以沿收敛方向进行搜索。

2.4 时间复杂度分析

假设目标函数评价单个解的时间复杂度为O（t0），四个搜索算子产生单个解的时间复杂度均为O（t1），目标函数评价次数为FE，则STASA的时间复杂度为O（FE×（t0+t1））。

在算法运行过程中，SE、NO、Tp以及t0、t1均为常数，与STASA相比，ASTSA算法的时间复杂度的量级没有变化。本次实验中，SE=100，NO=6，Tp=10，实际时间复杂度仅增加了O（2.86FE）。算法在自适应部分增加了一定的计算量，通过最优算子和参数增强算法的性能。

改进平移算子增加了方向确定部分的计算量，其他均与原平移算子相同。改进平移算子增加计算量的部分包括确定更优解、更劣解，计算均值，因此时间复杂度为O（SE），在实验中为常数复杂度。

3 仿真实验及分析

3.1 实验环境及参数设置

为了验证ASTSA的有效性，使用23个标准测试函数进行实验测试，并与STASA、STA、GSA、SCA［22］、WOA、GWO［18］、HGWOP［23］、VAGWO［24］共八个算法进行对比实验。然后使用八个带约束的工程设计问题来验证ASTSA在实际问题中的使用效果。

仿真实验所有程序均采用MATLAB R2021b进行编写、运行，运行环境为Windows 10 64位操作系统，硬件平台为Intel CoreTM i5-7300HQ CPU @ 2.50 GHz。每个算法的搜索强度SE、种群大小均设为100。每个对比算法的参数设置均与其原文保持一致，或者为经典参数设置，详见表1。

3.2 求解基准测试函数

本节使用基准测试函数对ASTSA进行测试，基准测试函数包括单峰、多峰的情况，F1～F7为单峰、F8～F23为多峰；且函数F1～F13的维度可变，在实验中均设置为30，F14～F23为固定维。详细定义如表2、3所示。

测试函数评价次数控制为500 000次，并且每个算法独立运行30次，记录其最优值min、30次运行的均值mean和标准差std。并将ASTSA与每个对比算法的30次独立运行的最优值min进行Wilcoxon符号秩和检验（显著性水平p＜0.05）。

3.2.1 求解结果分析

所有算法的测试结果如表4所示。其中R为Wilcoxon符号秩和检验的结果，1、0、-1分别表示ASTSA优于该算法、与该算法效果相同、劣于该算法；RankSum表示与该对比算法在23个测试函数上秩和检验的和，反映整体效果。表中粗体表示几个对比算法在当前测试函数的最优值。

由表4可知，除了F2、F3、F5、F6、F7、F12这六个测试函数以外，ASTSA在其他测试函数上能够取得最优的结果，并且在12个测试函数上达到了理论最优值，具有足够的求解精度。除了HGWOP以外，ASTSA与其他对比算法的Wilcoxon秩和检验结果RankSum均达到了12以上，且与HGWOP的RankSum也有2，证明ASTSA优于对比算法。

根据“No-free-lunch”准则，ASTSA算法在大部分测试函数上相较于原STASA取得了更好的结果，但也在函数F3上产生了“退步”，求解结果不如原STASA。改进后的ASTSA相对于原STASA的Wilcoxon秩和检验结果为18，证明了改进策略的有效性。与HGWOP相比，在23个测试函数中ASTSA占优的有F1～F4、F8～F10、F16、F18、F19、F21；HGWOP占优的有F5～F7、F12～F15、F20、F22，包含单峰可变维度、多峰可变维度以及多峰固定维的情况，没有明显的倾向。Wilcoxon秩和检验结果为2，ASTSA只是略优于HGWOP。

3.2.2 收敛性分析

图3为各个算法在部分测试函数（F1、F3、F4、F6、F9、F10）上的对数收敛曲线，分别代表不同的收敛情况。

其中，横坐标为评价次数，纵坐标为目标函数值的对数；并且每个算法均选取最优的一次进行绘制。在函数F1，ASTSA求解出了最优值，始终稳步收敛但速度相对于GWO和WOA较差；在函数F3，ASTSA没有达到最优结果，相对于原STASA产生了“退步”；在函数F4，ASTSA求解出最优值且收敛速度最快，但在后期出现了收敛速度减缓的趋势；在函数F6，ASTSA取得最优结果且收敛速度最快，但其前期收敛迅速而后期出现振荡的情况，即尝试“逃离”当前位置，寻找新的最优解，而HGWOP在F6上表现优异；在函数F9，多个算法均得到最优值，其中ASTSA速度最快；在函数F10，尽管ASTSA结果和收敛速度均为最优，但与其他算法一样在搜索后期陷入停滞。

综上，ASTSA能够在大部分基准函数上达到最优效果，但其收敛速度、局部搜索能力在部分问题上仍有缺陷（如F1、F3、F6），并且搜索后期开发能力也存在提升空间（如F4、F10）。

3.2.3 算法运行耗时

各算法的平均运行时间如图4所示。目标函数评价次数相同。23个测试函数中，ASTSA在15个测试函数上优于STASA，尽管ASTSA的时间复杂度有所增加，但其更强大的求解能力，能够更快找到最优解，因此在一些复杂问题上用时比STASA更短。

分别计算ASTSA与对比算法的耗时比例（ASTSA耗时/对比算法耗时×100%），然后计算23个测试函数的平均值，结果如表5所示，平均耗时比例均小于100%。按照平均耗时比例可以分为三档，第一档有STASA、STA，它们与ASTSA属于同一系算法，因其简明的搜索结果耗时最少；第二档为40～50%，包括SCA、WOA、GWO、HGWOP，平均耗时约为ASTSA的两倍；第三档为GSA、VAGWO，平均耗时达到ASTSA的10倍以上。

3.2.4 稳定性分析

单独从实验结果的标准差（表4中std）来看，ASTSA为最优的有7个，与GSA、GWO、HGWOP相同，为第一档。但其中GSA整体的求解效果并不理想，只在固定维度多峰测试函数中有良好的表现；而HGWOP求解效果优异（ASTSA与其的RankSum仅为2）。ASTSA与STASA相比优平劣为10/4/9，但STASA达到最优的仅有4个，少于ASTSA算法。

尽管ASTSA在F6等测试函数存在后期振荡的现象，但并未对稳定性造成过多影响，如ASTSA在F6的方差精度达到10-19，与GSA处于同一精度，仅次于最优的HGWOP。ASTSA算法在求解稳定性方面可与GSA、GWO、HGWOP同处于第一档，但GSA整体表现较差，HGWOP稍逊，ASTSA的综合求解能力最强。

3.3 自适应策略有效性检验

为了检验自适应策略的有效性，进行了简单的统计学检验。

a）自适应算子有效性检验。在测试函数的取值范围中随机生成当前解，使用自适应策略确定最优算子BestOp和最优参数值α*；然后使用最优算子BestOp以及另外两个算子进行搜索（均为最优参数值），记录产生的所有解中的最优解是否属于自适应确定的最优算子。在23个测试函数上分别进行1 000次，结果如图5所示，条形图为最优解属于最优算子的次数，横线为均值（1 000次/6个参数=166.67）。由图5可知，除测试函数F8以外，其余结果均达到均值以上，并在F1、F2等四个测试函数上达到1 000，且大于800的结果有9个，证明了自适应算子选择策略的有效性。

b）自适应参数有效性检验。与算子有效性检验类似，通过自适应策略确定最優参数后，使用参数集合进行搜索（最优算子），然后记录最优解是否属于最优参数值。在23个测试函数上分别进行1 000次，结果如图6所示。由图6可知，在每个函数上测试结果均大于均值，最差结果为235（F19），仍超出均值的40%，证明了自适应参数选择策略的准确、有效。

此外，图7、8分别为实际运行中各算子和参数值的平均调用次数（独立运行30次）。由图7可知，对于同一测试函数，不同算子的调用情况相差很大，并且对于不同的测试函数，不同算子的调用频率也不同。由图8可知，对于不同的测试函数，参数值的选择情况差别很大，从侧面佐证了自适应选择策略的有效性。

3.4 改进平移算子有效性检验

为验证修正方向的有效性，对改进平移算子进行有效性测试。在测试函数的取值范围中随机生成当前解，分别使用旋转算子、伸缩算子、轴向变换算子结合参数集合中每个参数进行搜索（SE=100），再分别使用原平移算子和改进平移算子进行搜索，对比改进前后平移算子产生新解中各自最优解的优劣。在23个测试函数中进行测试，分别以3个算子、每个参数（6个）各进行1 000次（共计1 000×3×6=18 000）并统计改进平移算子更优的次数，结果如图9所示。

由图9可知，在所有测试函数上测试结果均大于均值（9k），其中在F4上最差为9 172，其次F18为9 421，其余均大于10 000；在14个测试函数上超出均值的1/3（12 000），在8个上超出均值的1/2（13 500）。整体来看，改进平移算子优于原平移算子，且在一些函数（F1、F3、F5等）上具有优秀的效果。但整体效果没有达到最优，在部分测试函数上效果不明显（F4、F7等未达到1/3），没有在全部问题上达到跨越性的进步。

3.5 消融实验

为了进一步验证改进策略的有效性，本节进行消融实验，结果如表6所示，其中Adaption表示单独采用自适应策略、NewTrans表示单独采用改进平移算子，均与原STASA进行秩和检验。

单独采用自适应策略的算法与STASA相比，Wilcoxon秩和检验结果为12，整体效果较好；且采用改进平移算子之后达到18，进一步取得改善。单独采用改进平移算子的秩和检验结果为4，与改进平移算子有效性检验的结果接近，效果有所改善但没有跨越性进步。而在采用自适应策略的基础上增加改进平移算子，Wilcoxon秩和检验结果由12变为18，即改进平移算子与自适应策略有促进作用。

采用群智能算法种群平均策略来修正平移算子的搜索方向有一定的效果，但由于策略过于简单，无法对所有问题产生促进作用，因此可以在此基础上采用更高级的策略对搜索方向进一步修正，或采用其他群智能的高级搜索策略，使搜索的解不单单是“一条直线”，进而增强搜索效果。

3.6 求解带约束的工程设计优化问题

本节使用八个带约束的工程设计优化问题来进一步评估ASTSA的有效性。分别是压缩/拉伸弹簧、工字梁、焊接梁、悬臂梁、管柱、三杆桁架、减速器、活塞杆共八个设计问题［25］，约束条件个数分别为2、7、1、6、11、4，如图10所示。

将ASTSA和STASA以及社交网络搜索（social network search，SNS）［25］算法分别运行30次，并保证相同的评价次数，结果如表7所示。可以看到，在压缩/拉伸弹簧设计问题上，ASTSA的求解结果不如SNS，而在其他七个问题中均得到了最优的结果。在三杆桁架和减速器设计问题中，ASTSA与SNS都求解到了最优值，但ASTSA的均值不如SNS，即ASTSA求解的稳定性仍存在不足。

ASTSA与原STASA和SNS的Wilcoxon秩和检验结果分别为7和1，即与STASA相比，本文算法所做改进使算法效果得到了提升。且整体优于对比算法SNS，具有良好的求解效果。通过实验证明了ASTSA算法能够在带约束的实际工程设计优化问题中应用求解。

4 结束语

本文针对STASA的不足提出了一种自适应状态转移模拟退火算法（ASTSA）。首先使用统计方法引入自适应策略，根据生成解的情况自适应选择最优的算子和参数值；然后针对平移算子的不足，借鉴群智能算法种群“平均解”的思路，修正平移算子的搜索方向，增强算子的稳定性。通过在23个基准测试函数以及8个工程设计优化问题以及Wilcoxon秩和检验验证了ASTSA的有效性，并分析了其不足。在未来的研究中，将针对ASTSA在求解复杂问题时稳定性不足的问题进行改进，提高其适用能力。

参考文献：

［1］Goldberg D E.Genetic algorithm in search，optimization，and machine learning［M］.Boston，MA：Addison-Wesley Longman Publishing Co.，Inc.，1989.

［2］Stron R，Price K.Differential evolution：a simple and efficient adaptive scheme for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11（12）：341-359.

［3］Kennedy J，Eberhart R.Particle swarm optimization［C］//Proc of International Conference on Neural Networks.Piscataway，NJ：IEEE Press，1995：1942-1948.

［4］Mirjalili S，Lewis A.The whale optimization algorithm［J］.Advances in Engineering Software，2016，95（5）：51-67.

［5］Kirkpatrick S，Jr Gelatt C D，Vecchi M P.Optimization by simulated annealing［J］.Science，1983，220（4598）：671-680.

［6］Rashedi E，Nezamabadi-Pour H，Saryazdi S.GSA：a gravitational search algorithm［J］.Information Sciences，2009，179（13）：2232-2248.

［7］Atashpaz-Gargari E，Lucas C.Imperialist competitive algorithm：an algorithm for optimization inspired by imperialistic competition［C］//Proc of IEEE Congress on Evolutionary Computation.Piscataway，NJ：IEEE Press，2007：4661-4667.

［8］Shi Yuhui.Brain storm optimization algorithm［C］//Proc of the 2nd International Conference on Swarm Intelligence.Berlin：Springer，2011：303-309.

［9］Han Xiaoxia，Dong Yingchao，Yue Lin，et al.State transition simulated annealing algorithm for discrete-continuous optimization problems［J］.IEEE Access，2019，7：44391-44403.

［10］Zhou Xiaojun，Yang Chunhua，Gui Weihua.State transition algorithm［J］.Journal of Industrial & Management Optimization，2012，8（4）：1039-1056.

［11］周曉君，阳春华，桂卫华.状态转移算法原理与应用［J］.自动化学报，2020，46（11）：2260-2274.（Zhou Xiaojun，Yang Chunhua，Gui Weihua.The principle of state transition algorithm and its applications［J］.Acta Automatica Sinica，2020，46（11）：2260-2274.）

［12］Chu Junwen，Dong Yingchao，Han Xiaoxia，et al.Short-term prediction of urban PM2.5 based on a hybrid modified variational mode decomposition and support vector regression model［J］.Environmental Science and Pollution Research，2021，28（1）：56-72.

［13］Shen Yadi，Dong Yingchao，Han Xiaoxia，et al.Prediction model for methanation reaction conditions based on a state transition simulated annealing algorithm optimized extreme learning machine［J］.International Journal of Hydrogen Energy，2023，48（64）：24560-24573.

［14］Zhang Yan，Han Xiaoxia，Dong Yingchao， et al.A novel state transition simulated annealing algorithm for the multiple traveling salesmen problem［J］.Journal of Supercomputing，2021，77（10）：11827-11852.

［15］Zhou Xiaojun，Yang Chunhua，Gui Weihua.A statistical study on parameter selection of operators in continuous state transition algorithm［J］.IEEE Trans on Cybernetics，2019，49（10）：3722-3730.

［16］董颖超，张宏立，王聪.带有策略自适应的状态转移算法［J］.控制与决策，2022，37（3）：574-82.（Dong Yingchao，Zhang Hongli，Wang Cong.State transition algorithm with strategy adaptation［J］.Control and Decision，2022，37（3）：574-582.）

［17］Dong Yingchao，Zhang Hongli，Wang Cong，et al.An adaptive state transition algorithm with local enhancement for global optimization［J］.Applied Soft Computing，2022，121（5）：108733.

［18］Mirjalili S，Mirjalili S M，Lewis A.Grey wolf optimizer［J］.Advances in Engineering Software，2014，69（3）：46-61.

［19］郭振洲，劉然，拱长青，等.基于灰狼算法的改进研究［J］.计算机应用研究，2017，34（12）：3603-3606，3610.（Guo Zhenzhou，Liu Ran，Gong Changqing，et al.Study on improvement of gray wolf algorithm［J］.Application Ｒesearch of Computers，2017，34（12）：3603-3606，3610.）

［20］Heidari A A，Mirjalili S，Faris H，et al.Harris hawks optimization：algorithm and applications［J］.Future Generation Computer Systems，2019，97（8）：849-872.

［21］李雅梅，孟嗣博，陈雪莲.多策略改进的天鹰优化算法及其应用［J］.计算机应用研究，2023，40（5）：1352-1359.（Li Yamei，Meng Sibo，Chen Xuelian.Multi-strategy improved aquila optimizer and its application［J］.Application Research of Computers，2023，40（5）：1352-1359.）

［22］Mirjalili S.SCA：a sine cosine algorithm for solving optimization problems［J］.Knowledge-Based Systems，2016，96（3）：120-133.

［23］Zhang Xinming，Lin Qiuying，Mao Wentao，et al.Hybrid particle swarm and grey wolf optimizer and its application to clustering optimization［J］.Applied Soft Computing，2021，101（3）：107061 .

［24］Rezaei F，Safavi H R，Elaziz M A，et al.An enhanced grey wolf optimizer with a velocity-aided global search mechanism［J］.Mathema-tics，2022，10（3）：351.

［25］Bayzidi H，Talatahari S，Saraee M，et al.Social network search for solving engineering optimization problems［J］.Computational Intelligence and Neuroscience，2021，2021：8548639.