基于领导者竞争策略的改进猎人猎物优化算法

常耀华 韦根原

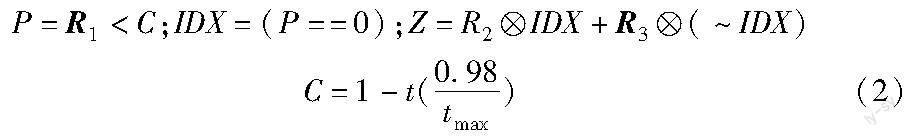
摘 要：针对猎人猎物优化算法寻优精度低和易陷入局部最优等问题，提出了一种基于领导者竞争策略的改进猎人猎物优化算法。首先将种群随机分为三个亚群，采用不同的搜索策略，扩大搜索范围；其次，采用精英组合突变策略，提升种群子代多样性，规避局部最优值；最后，提出领导者竞争策略，利用个体间的信息交流，统合各个策略，筛选出最优变量。通过数值实验以及在工程优化问题上的应用结果表明，所提算法相较于对比算法具有更为优异的寻优能力，验证了改进策略的有效性和可靠性。

关键词：猎人猎物优化算法；精英组合突变策略；领导者竞争策略；均值搜索策略；正余弦策略

中图分类号：TP18   文献标志码：A   文章编号：1001-3695（2024）01-021-0142-08

doi：10.19734/j.issn.1001-3695.2023.05.0222

Improved hunter prey optimization algorithm based on leader competitive strategy

Abstract：Aiming at the problems of low optimization accuracy and easy to fall into local optimization of hunter prey optimization algorithm，this paper proposed an improved hunter prey optimization algorithm based on leader competitive strategy.Firstly，this paper randomly divided the population into three subgroups and adopted different search strategies to expand the search scope.Secondly，it adopted an elite combination mutation strategy to enhance the diversity of population offspring and avoid local optima.Finally，it proposed a leader competitive strategy，used the information exchange between individuals，integrated various strategies，and screened out the optimal variables.Through numerical experiments and application to engineering optimization problems，the results show that the proposed algorithm has better optimization ability than the comparison algorithm，veri-fying the effectiveness and reliability of the improved strategy.

Key words：hunter prey optimization algorithm；elite combination mutation strategy；leader competitive strategy；mean search strategy；sine cosine strategy

0 引言

許多工程应用和科学研究中出现的问题都可以直接转换为优化问题［1］，但由于这类问题存在许多决策变量和约束条件，同时需要在巨大而复杂的搜索空间寻找其最优解或可接受的解，所以传统优化方法往往难以解决这些问题。因此，在过去几年中，受自然现象或规律启发的元启发式算法得到了迅速的发展，并在许多复杂的优化问题上广泛应用［2］。

尽管目前的智能优化算法种类繁多且性能优异，但是由NFL理论［3］可知，没有一种算法可以适用于所有情况，因此学者们仍致力于开发算法，为全局优化问题提供新的可能。

猎人猎物优化（hunter-prey optimization，HPO）算法［4］于2022年底提出的一种全新的智能优化算法，具有调节参数少、收敛速度快等优点，在一些工程优化问题中有着出色的表现。许建伟等人［5］将HPO算法与小波包变换和极限学习机结合构成径流多步预报模型，相较于其他算法，极大提高了预报准确性。高雨虹等人［6］将HPO算法与长短时记忆网络结合构成组合模型，用于出车率预测，与经典算法相比，该模型具有更出色的表现。但根据算法的机理可知，HPO虽然具有较强的开发能力，但仍存在全局寻优能力较弱、收敛精度有限等问题。Fu等人［7］提出了IHPO算法，利用增强型SCA算法优秀的全局搜索能力弥补HPO算法的弱点，鲁英达等人［8］提出一种LHPO算法，采用混沌策略对种群优化，增加初始种群的多样性，并利用莱维飞行策略规避局部极值。

以上改进对HPO算法的搜索性能虽然有一定的提升，但面对高维复杂优化问题时，算法仍存在全局探索不充分，容易陷入局部极值导致搜索停滞等问题。对于这些问题的解决方案，目前优化算法的主流策略注重于对算法的运行行为逻辑和初始种群位置的改进，保留最优值并让种群内的个体向最优值方向收敛［9，10］。这类改进策略一定程度上提升了算法的优化能力，但以全局最优值为中心，忽视了个体之间的信息交流。Li等人［11］提出了一种新型竞争策略，通过将变量分层分类进行竞争和学习，使每个变量都有自己的学习行为，增强种群的多样性。但该种方法不可避免地会增加无用的计算成本。综合以上，本文在发挥最优个体的领导优势的基础上，从优秀个体之间的协同学习和竞争的角度提出一种基于领导者竞争策略的改进猎人猎物优化算法（improved hunter prey optimization algorithm based on leader competitive strategy，LCIHPO）。首先采用不同的更新机制更新不同的亚群以此提升算法搜索范围，提出一种精英组合变异策略，提升子代多样性，规避局部最优值。最后，提出一种领导者竞争策略，通过最优个体间的竞争和交流，使用有限的计算成本统合各个策略优势，提升算法的综合性能。

1 猎人猎物优化算法

HPO算法是一种新颖的元启发式算法，算法全程可以分为探索和开发两个阶段。猎人寻找猎物并追逐的行为便是算法的探索过程，对于猎人的搜索机制，如式（1）所示。

xi，j（t+1）=xi，j（t）+0.5［（2CZHpos（j）-xi，j（t））+

（2（1-C）Zμ（j）-xi，j（t））］（1）

其中：t为迭代数；xi，j（t）是猎人当前所在位置；xi，j（t+1）是猎人下一个位置；Z是自适应调节参数；C是平衡算法探索和开发能力的参数，由1向0.02递减；Hpos（j）是猎物所在位置。

相关参数的计算如式（2）所示。

其中：R1和R3是［0，1］的随机向量；tmax是最大迭代数。

按照猎人捕杀猎物的行动准则，距离群体最远的个体会被当作猎物，但为了避免选择猎物而导致的延迟收敛问题，加入一种递减机制，随着猎物死亡，可选位置减少，从而得到一种新的猎物位置等式，如式（3）（4）所示。

其中：kbest是引入的递减机制；N为种群数量；Deuc为每个变量与平均位置的欧几里德距离；μj为平均距离。

猎物为了生存而逃跑的行为便是算法的开发阶段，假设可以让猎物安全逃跑的位置便是全局最优解，开发阶段搜索机制如式（5）所示。

xi，j（t+1）=Gbest（j）+CZ cos（2πR4）×（Gbest（j）-xi，j（t））（5）

其中：xi，j（t）是猎物当前位置；xi，j（t+1）是猎物下次移动位置；Gbest（j）是全局最佳位置；R4是［-1，1］的随机数。

综合以上可以得出HPO算法的更新机制，如式（6）所示。

其中：R5是［0，1］的随机数；B是一个协调参数，设置为0.1。当R5的值小于B时，代理搜索点被认为是猎人的位置，开展猎人搜素机制。反之，则认为代理搜索点是猎物的位置，开展猎物位置更新机制。

2 LCIHPO算法

2.1 HPO算法变体

1）基于均值搜索策略的獵人猎物算法（hunter prey optimization algorithm based on mean search strategy，MSHPO）

在HPO算法中，猎人的全局搜索机制受猎物所在位置以及所有可能猎物的平均位置的影响，若要提升寻得全局最优解的可能性，则必须扩大搜索区间。文献［12］提出了一种基于均值搜索策略的MSPSO算法，利用均值策略平衡全局和局部寻优的能力，扩大了算法的搜索范围。本文将均值搜索策略引入HPO算法中，使用决策变量的个体最优值和全局最优值的线性组合取代猎物位置和平均位置，引导变量更新，新的猎人搜索机制公式为

其中：Pbest为个体历史最优值。

2）基于正余弦策略的猎人猎物算法（hunter prey optimization algorithm based on sine-cosine strategy，SCHPO）

受SCA算法［13］决策变量更新公式的启发，本文通过引入正余弦模型震荡特性对猎物行动模式产生的影响，维持猎物位置的多样性，进而提升种群内个体的寻优能力，减少陷入局部最优的可能，改进猎物位置更新公式为

其中：r1，r2为［0，1］均匀分布的随机数。

2.2 精英组合突变策略

HPO算法在解决高维多极值的复杂优化问题时，往往存在容易陷入局部最优值区和多样性差等问题。在算法中引入突变算子，可以有效提高子代的随机性，使算法避免过早陷入局部最优值导致探索停滞，从而提升算法的寻优效能。

Hu等人［14］采用单个突变算子策略，使用自适应策略选择突变率，根据突变率在合适的阶段采用突变算子。但面对现实中复杂的优化问题时，往往很难准确地判断算法所处阶段，若采用错误的突变算子便会影响算法对最优值的寻取效率。Wang等人［15］采用一种基于个体适应度值的突变算子选择策略，通过对比变异前后个体的适应度值高低，判断下一次迭代是否继续采用该突变算子。这种方法平衡了突变算子的探索和开发能力，但该策略相对失去了一定的随机性，降低了子代的多样性。

综上所述，本文提出一种精英组合突变策略：为了提高突变的随机性，选用组合突变算子的形式；为了保证算子选择的合理性，将基于个体适应度值的突变算子选择策略作为组合突变算子的选择机制；为了保证突变的有效性，构建精英池，采用精英池中的粒子作为突变变量。精英池中的粒子用于帮助提升种群的多样性，因此精英粒子需要含有尽量多的优秀且多样的信息，选用种群中每个粒子的个体历史最优解存储在精英池中，如式（9）所示。

其中：F为比例因子；x′（t）为变异个体；mr1、mr2、mr3、mr4、mr5为随机整数，mr1≠mr2≠mr3≠mr4≠mr5≠i。

组合突变算子中，式（10）突变算子具有较强的探索能力，收敛速度较慢，不容易陷入局部最优，式（11）突变算子具有很强的开发能力，收敛速度快，但容易陷入局部最优。根据调节因子u选择突变方式。

为了保证充分变异的同时兼顾计算效率，令突变因子p为［0，1］的随机数，当p小于变异概率pm时进行变异，反之则不进行。经过多次实验对比，当pm=0.7时，变异效果最好。

精英组合突变策略伪代码为

输入：更新后的种群。

输出：变异种群的全局最优值Gbestmu；最优适应度值fitmu。

更新精英池

for i=1：N

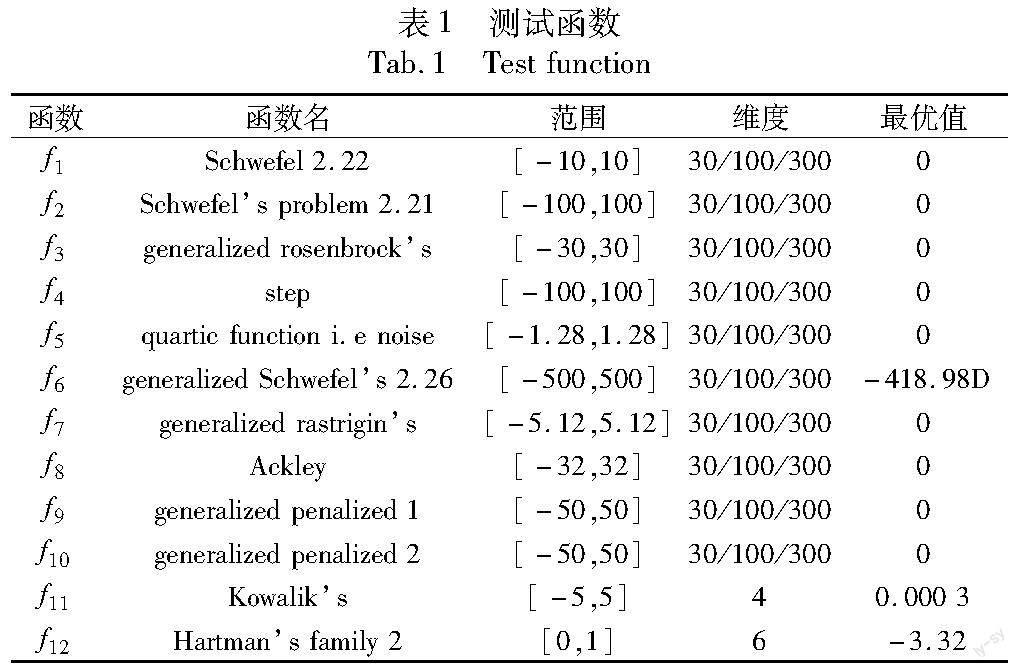
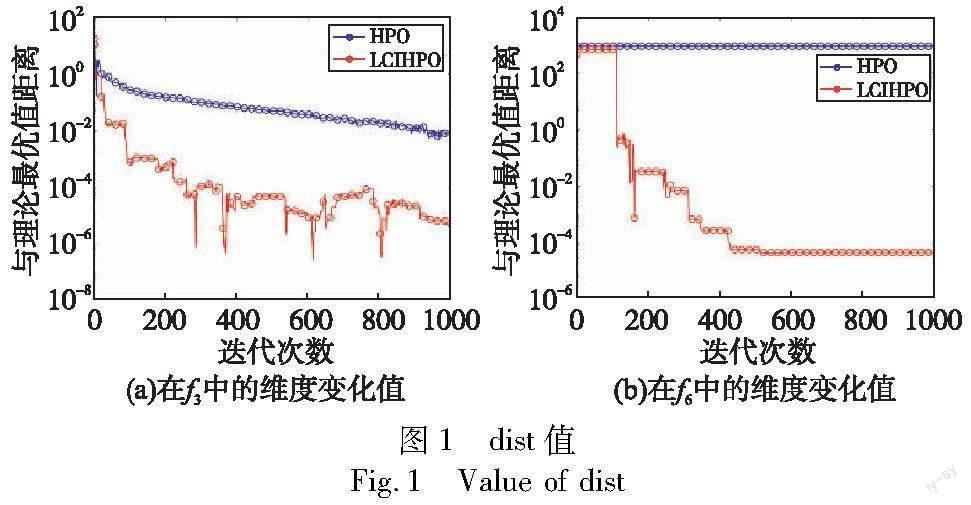
if p

if u=1

采用式（10）突变；

更新调节因子；

end

if u=0

采用式（11）突变；

更新调节因子；

end

else

xi′=e（i）

end

更新全局最优值和适应度值；

end

2.3 领导者竞争策略

如前文所述，HPO算法的每种变体以及突变策略都有其独有的优势，为了更好地提升算法综合效能，本文提出领导者竞争策略，将上文中执行不同搜索策略的三个亚群和突变种群的最优值带入到领导者竞争策略中，领导者策略执行步骤为

a）将三个亚群和变异种群的最优值作为领导者。

b）将领导者按照适应度值排序，选取最优和次优领导者。

c）次优领导者向上一级领导者学习经验，如式（13）所示。

leaderkrandj（t）←leaderk-1randj（13）

其中：k为次优领导者排序k=2，3，4；randj为随机某个维度，randj∈（1，dim）。

d）最优领导者和次优领导者展开自学习。

e）重新进行领导者排序，选出最优领导者作为全局最优值。

2.3.1 次优领导者自学习

反向学习策略通常应用于初始化种群，可以得到很好的一组初始值，将反向学习策略应用于算法搜索策略中，也可以提升算法全局寻优能力，规避局部最优。但是通过反向学习得到解是固定的，若已经陷入局部最优，则很难跳出。透镜成像策略［16］是一种基于凸透镜成像规律的反向学习策略，该方法可以动态地调整反向解，进一步提升优化能力。将该方法以及思想引入，本文提出一种基于透镜成像的动态反向搜索策略。

透镜成像反向点计算公式如式（14）所示。

其中：L=1，2，3，4为领导者序号；r3为［0，1］的随机数。

在实际搜索过程中，搜索空间往往是动态的，反向学习亦然，因此边界为

lb=min（x（t）），ub=max（x（t））（16）

动态反向搜索策略具有不对称性和动态变化特征，可以引导个体在搜索空间中向相反解学习，提高勘探能力，从而增加实现最优解决方案的可能性，计算公式为

leader′L=leaderL+r4（r5xnback-leaderL）（17）

其中：r4，r5为［0，1］的随机数；leader′L为反向学习得到的新个体。

自学习后采用贪婪算法比较两者适应度值，保留优势个体，如式（18）所示。

其中：f（·）为适应度函数。

2.3.2 最优领导者自学习策略

最优领导者进行自学习以防止被替换，采用个体适应度值选择机制，在算法迭代前期，最优领导者应当搜索尽可能大的区域，寻找全局最优值，采用上文提出的基于透镜成像的动态反向搜索策略进行更新。在算法迭代后期，全局最优解很大概率在最优个体附近，因此采用融合莱维飞行的阿基米德螺旋机制［17］提高算法的局部开采收益，该机制借助阿基米德螺线的旋转特征，以一定角度和步距探索个体的邻域范围，可最大限度保证开采的周密性。莱维飞行解计算公式如式（19）所示。

其中：α表示步长变量；xrand（t）表示随机生成的个体；u，v为正态分布的随机数；β=1。

融合莱维飞行设为阿基米德螺线更新机制公式为

leader′1（t）=leader1（t）+|leader1（t）-xlevy（t）|r6 cos（2πr6）（20）

其中：leader1（t）为最优领导者；leader′1（t）为更新后的最优领导者；r5为［-1，1］的随机数。为了保证更新后的个体优于原个体，采用式（18）的贪婪算法进行判定。

2.4 LCIHPO算法流程

LCIHPO算法的伪代码如下：

输入：种群规模N；维度D；最大迭代次数tmax。

输出：猎物安全位置xbest以及适应度fit。

for t=1：tmax

计算个体适应度值，得出当代最優个体以及个体历史最优值

将种群随机均分为三个亚群，分别为N1、N2、N3

for i=1：N1

按照式（6）更新种群；

对比全局最优值并进行择优取代，得到Gbest1 ；

end

for i=1：N2

按照式（5）（7）更新种群

对比全局最优值并进行择优取代，得到Gbest2；

end

for i=1：N3

按照式（1）（8）更新种群

对比全局最优值并进行择优取代，得到Gbest3；

end

采用精英组合变异策略，得到最优变异个体Gbestmu；

将Gbest1、Gbest2、Gbest3、Gbestmu带入领导者竞争策略中，筛选出最优个体；

更新全局最优个体和其适应度值；

end

2.5 时间复杂度分析

时间复杂度主要取决于算法结构的复杂程度，对于HPO算法，主要在于产生初始种群、猎人位置更新、猎物位置更新和适应度值评估四个阶段。对于种群规模为N，决策变量维度为D，迭代数为T的解决方案，算法初始化时间复杂度O（N×D），猎人变量更新时间复杂度为O（（1-B）×T×N×D），猎物位置更新的时间复杂度为O（B×T×N×D），参数B为协调参数，取值为0.1，全局最优值评定与更新的时间复杂度为O（T×N×D） ，从而可以得到HPO算法的时间复杂度。

O（HPO）=O（T×N×D）（21）

LCIHPO算法的时间复杂度包括HPO和改进HPO算法更新三个亚群，分别进行择优取代保留最优值，因此时间复杂度为O（N×D×T）；精英池更新时间复杂度为O（N×T）；组合变异策略时间复杂度为O（N×T）；领导者竞争策略时间复杂度为O（4×T）综合以上环节，处理高维优化问题时，时间复杂度可进行近似处理，由此可得LCIHPO算法的时间复杂度为

O（LCIHPO）=O（T×N×D）（22）

式（21）（22）相比相差不大，综上可知改进算法并没有增加过大的计算负担。

3 数值仿真分析

3.1 实验设计与参数设置

为了验证本文LCIHPO算法的理论优化能力，设计五组理论仿真实验，分别为：算法精度和搜索范围分析；HPO算法和其改进算法的对比分析；与其他智能算法以及改进算法在不同维度下的对比和低维下的迭代趋势分析；Wilcoxon秩和检验；CEC2014复杂测试函数的仿真。

本文选取12个基准测试函数。如表1所示，f1～f5为单峰测试函数，f6～f10为多峰测试函数，f11～f12为固定维度测试函数。本次仿真实验的系统运行环境为Intel CoreTM 12th i5-12500H CPU@3.10 GHz，系统内存16 GB，软件运行环境为MATLAB 2021b，种群规模N=30，维度D=30/100/300，最大迭代次数T=1000，每种算法独立重复运行30次。

3.2 精度和搜索范围分析

优化算法的目标是求取问题的最优值，而测试函数的理论最优值和最优解是已知的，因此可以通过对比每次迭代得出的实际最优解和理论解之间相应维度位置变化来分析算法在迭代过程中的搜索精度和范围。距离表达式如式（23）所示。

dist（t）=|Gbest（j）′-Gbest（j）|（23）

其中：Gbest（j）′为维度j的理论最优解。选择单峰测试函数f3和多峰测试函数f6进行测试，维度选为30，j为5，测试结果如图1所示。

从图1可以看出，在单峰函数f3中，HPO得到的距离值虽然随着迭代逐步下降，但在有限迭代次数内未突破10-2，而LCIHPO的最终距离值达到了10-6。从距离值曲线来看， LCIHPO相比于HPO，其波动性更强，因此可以得知LCIHPO具有更强的优化性能以及多样性。在多峰函数f6中，HPO的距离值近似为一条直线，而LCIHPO的距离曲线在迭代前中期大幅下降，突破10-4后下降速度降低。因此可以得知HPO陷入局部最优值且搜索停滞，而LCIHPO在探索前期规避了局部最优值，并持续突破最小值。以上证明了本文策略不仅提高了算法的收敛精度，同时提升了算法的波动性，从而扩大了算法的搜索范围，提升了得到全局最优值的可能。

3.3 算法变体有效性分析

为了证明本文算法变体策略的有效性，将本文提出的HPO变体算法MSHPO、SCHPO与HPO算法进行测试，维度为30，具体结果如表2所示。

由表2可知，在单峰函数f1～f5中，SCHPO在f1中各项指标收敛至理论最优值，在f2～f5中尽管没有收敛至最优值，但大部分指标优于HPO算法，由此可知，正余弦策略的震荡特性有效提升了算法的局部开发能力。MSHPO在单峰函数测试中略逊于SCHPO，但仍优于HPO，在f5中最优值优于对比算法，表明该搜索策略仍保持一定优势。在多峰测试函数f6～f10中，MSHPO相关指标相较于对比算法表现较为优异，表明均值搜索策略扩大了搜索空间，有效地规避局部极值问题。在固定维函数f11、f12中，三种策略均有一定的优点，评价指标数值差距并不明显。综合以上可知，HPO的两种算法变体在不同测试函数中各有优势，整体上优化性能较优于改进前算法。

3.4 与HPO算法及相关改进算法对比分析

为了证明本文算法相比其他文献改进HPO算法具备更优的竞争力，将本文算法与HPO、IHPO、LHPO算法在D=30条件下进行对比分析，对比结果如表3所示。

分析表3可知，本文算法明显优于HPO和对比改进算法，在f1、f2、f6、f7、f12中收敛至理论最优值，在其他测试函数中尽管没有收敛至最优值，但最优值和平均值优于对比算法，搜索精度相比于其他算法最高。在单峰函数f3中，LCIHPO的标准差低于HPO，但最优值和平均值远高于HPO。在多峰函数f6～f10中，LCIHPO各项指标均优于对比算法，在f10中，最优值更是高出HPO算法13个数量级，表明本文算法可以克服局部极值对寻优的影响。在固定维函数f11、f12中，LCIHPO寻优能力仍处于领先地位。总体来看，本文算法在不同函数上均值基本都是最好的表现，且优于其他算法，表明本文算法相对于先前改进HPO算法更具有竞争力。

3.5 不同维度下算法对比分析

为了验证本文算法在不同维度下的求解优势，选用粒子群算法（particle swarm optimization，PSO）［18］、SCA、鵜鹕算法（pelican optimization algorithm，POA）［19］、IPSOVP［20］、DSCA［21］与LCIHPO算法在12个不同维度的基准测试函数上进行对比分析，f11、f12为固定维度测试函数，维度设定如表1所示，相关参数按照对应文献中设置。取平均值、标准差和最优值作为评定标准，具体测试结果如表4、5所示。

由表4、5可知，在不同维度下的单、多峰函数以及固定维度函数上，LCIHPO的寻优性能整体优于对比算法。首先，纵向来看，在维度为30的条件下，LCIHPO算法在f1、f3、f6、f7中收敛至全局最优值，在其余测试函数中未寻到全局最优值但搜索精度仍强于对比算法。在求解单峰函数f4中， LCIHPO算法平均值收敛精度和标准差方面比PSO算法高19个数量级，表明其具有优异的收敛精度和稳定性。在求解多峰函数中，LCIHPO的各项指标均优于对比算法，表明算法可以很好地克服局部极值的不利影响并以优异的态势进行全局最优值探索。横向来看，随着维度的升高，可以看到所有算法的各项指标均发生不同程度的改变，而LCIHPO受维度上升的影响最小。在f1、f2、f6、f7中，LCIHPO算法不受维度上升的影响，平均值和最优值仍能收敛至全局最优值。在300维度时，LCIHPO在10个测试函数中平均值排行第一，标准差和最优值有9个排行第一，综合可得LCIHPO对维度变化适应性较强。在固定维度函数中，LCIHPO在f12中平均值和最优值寻到理论最优值，且标准差较小，尽管在f11中没有收敛至理论最优值，但各项指标优于对比算法，算法整体性能优异。总体来看，LCIHPO在不同维度条件下的不同函数中均展现了良好的寻优能力，证明了本文算法的优越性。为了更加直观地展现算法迭代过程，在维度为30的条件下，各个算法在部分函数中的迭代寻优曲线如图2所示。

通过图2可以观察到，LCIHPO能够以较快的速度收敛到最优值，在图2（a）（b）中，LCIHPO用了较少的迭代次数便收敛到了理论最优值。在图2（c）中，在其他算法陷入搜索停滞时，LCIHPO仍能不断探索突破最小值，反映了算法优异的收敛速度和精度。在图2（f）～（h）中，可以看到LCIHPO以较快速度收敛至最优值，收敛速度优于其他算法，而在图2（i）（j）中，可以看到当其他算法陷入局部极值时，LCIHPO仍能以较快的速度继续向最优解靠拢，可以看出算法具有较强的规避局部极值陷阱的能力。通过迭代曲线对比，验证了本文算法具有良好的收敛速度和精度，更加直观地展示了算法规避局部极值的能力。

3.6 Wilcoxon秩和检验

为了探究本文算法的改进优越性，在显著水平p=5%条件下，搜索维度为30，采用Wilcoxon秩和检验来验证LCIHPO算法是否与上文中参与对比的算法存在显著差异，验证结果如表6所示。其中：N/A表示性能相近而无法比较；+、-、=分别表示LCIHPO性能优于、劣于、近似于对比算法。

通过表6可以得知，在12个测试函数中，绝大多数的p值小于5%，总体上反映了LCIHPO算法与对比算法具有显著差异，且寻优性能优于对比算法。

3.7 CEC2014复杂函数分析

为了进一步验证本文算法寻优的有效性，选取部分CEC2014复杂函数进行仿真分析。选取的函数类型分别为单峰（UN）、多峰（MN）、混合类型（HF）以及复合类型（CF），如表7所示。将本文算法与PSO、SCA、HPO、POA、IPSOVP、IHPO、DSCA、LHPO进行对比分析，以平均值与标准差作为评定指标，重复运行40次，测试结果如表8所示。

由表8可知，在单峰测试函数CEC01中，本文算法的各项指标均优于对比函数，表明其具有更佳的求解精度；在求解多峰测试函数时，虽然CEC16上IPSOVP的标准差领先其他算法，但LCIHPO的平均值更接近理论最优值；对于混合函数，本文算法在各个函数上均有优异的表现，表明了其具有良好的稳定性；在复合类型函数中，本文算法收敛到一定值并不再发生改变，且得到的平均值优于对比算法，反映其更善于解决此类问题。综合以上可以得知，本文算法在复杂函数上仍能有优异的表现，验证了本文算法优秀的鲁棒性。

4 工程优化问题的应用

为了验证本文算法在实际工程应用中的性能，选取了压力容器设计这一经典的工程优化问题。在该设计问题中，压力容器两端均有封盖，其中头部一端为半球状，包括四个决策变量，分别为容器壁厚度Ts、头部厚度Th、圆柱内壁半径R和圆柱截面长度L。该问题数学模型为

a）决策变量

x=［x1，x2，x3，x4］=［Ts，Th，R，L］（24）

b）目标函数

f（x）min=0.6224x1x3x4+1.7781x2x23+3.1661x21x4+19.84x21x3（25）

c）约束条件

d）边界约束

0≤x1≤99，0≤x2≤99

10≤x3≤200，10≤x4≤200（27）

将本文算法与HPO、PSO、POA、HHO、DSCA、LHPO以及IHPO算法进行对比，得到結果如表9所示。

由表9可知，本文算法在八种优化算法中取得了最优解决方案，最终得到的最小成本为5 884.311 71，证明了本文算法在工程案例中的适用性和可靠性。

5 结束语

本文提出一种基于领导者竞争策略的改进HPO算法。将初始种群分为三个亚群，采用不同的更新策略以此产生不同的步长，确保算法在不同阶段的探索开发能力；引入精英组合变异策略，依据个体历史最优值进行变异，减少算法陷入局部最优的概率；最终将亚群和变异种群产生的最优子代带入领导者竞争策略中，通过最优个体间的信息交流和竞争，统合各个策略的优势。数值仿真实验的结果表明，本文算法比其他改进HPO算法更具有竞争力，在面对不同维度的不同函数时均具有较稳定的寻优能力以及优异的显著性差异，而CEC2014函数的仿真则证明了算法的有效性和鲁棒性。最后在压力容器设计优化问题上分析验证了LCIHPO在解决工程优化问题上的可靠性。未来可进一步将该算法应用到电力、热工系统相关领域。

参考文献：

［1］Deng Wu，Shang Shifan，Cai Xing，et al.Quantum differential evolution with cooperative coevolution framework and hybrid mutation strategy for large scale optimization［J］.Knowledge-Based Systems，2021，224：107080.

［2］Wang Xi，Sheng Mengmeng，Ye Kangfei，et al.A multilevel sampling strategy based memetic differential evolution for multimodal optimization［J］.Neurocomputing，2019，334：79-88.

［3］Wolpert D H，MacReady W G.No free lunch theorems for optimization［J］.IEEE Trans on Evolutionary Computation，1997，1（1）：67-82.

［4］Naruei I，Keynia F，Sabbagh M A.Hunter-prey optimization：algorithm and applications［J］.Soft Computing，2022，26：1279-1314.

［5］許建伟，崔东文.WPT-HPO-ELM径流多步预报模型研究［J］.水资源与水工程学报，2022，33（6）：69-76.（Xu Jianwei，Cui Dongwen.Research on WPT-HPO-ELM multistep run off prediction model［J］.Journal of Water Resources and Water Engineering，2022，33（6）：69-76.）

［6］高雨虹，曲昭伟，宋现敏.基于猎人猎物优化与双向长短时记忆组合模型的汽车出车率预测［J］.交通运输系统工程与信息，2023，23（1）：198-206，264.（Gao Yuhong，Qu Zhaowei，Song Xianmin.Prediction of car trip rate based on hunter hunt optimization and bidirectional long short term memory combination model［J］.Transportation System Engineering and Information，2023，23（1）：198-206，264.）

［7］Fu Mingxin，Liu qiang.An improved hunter-prey optimization algorithm and its application［C］//Proc of IEEE International Conference on Networking，Sensing and Control.Piscataway，NJ：IEEE Press，2022：1-7.

［8］鲁英达，张菁.基于改进猎人猎物算法的VMD-KELM短期负荷预测［J/OL］.电气工程学报.（2023-04-04）.http：//kns.cnki.net/kcms/detail/10.1289.tm.20230403.1811.009.html.（Lu Yingda，Zhang Jing.VMD-KELM short-term load forecasting based on improved hunter prey algorithm［J/OL］.Journal of Electrical Engineering.（2023-04-04）.http：//kns.cnki.net/kcms/detail/10.1289.tm.20230403.1811.009.html.）

［9］王英聪，刘驰，王延峰.基于刺激-响应机制的改进鸡群算法［J］.控制与决策，2023，38（1）：58-66.（Wang Yingcong，Liu Chi，Wang Yanfeng.Improved flock algorithm based on stimulus-response mechanism［J］.Control and Decision，2023，38（1）：58-66.）

［10］周鹏，董朝轶，陈晓艳，等.基于Tent混沌和透镜成像学习策略的平衡优化器算法［J］.控制与决策，2023，38（6）：1569-1576.（Zhou Peng，Dong Chaoyi，Chen Xiaoyan，et al.Balanced optimizer algorithm based on Tent chaos and lens imaging learning strategy［J］.Control and Decision，2023，38（6）：1569-1576.）

［11］Li Taiyong，Shi Jiayi，Deng Wu，et al.Pyramid particle swarm optimization with novel strategies of competition and cooperation［J］.Applied Soft Computing，2022，121：108731.

［12］陆松建，司伟立，韩娟，等.逃逸均值简化粒子群优化算法［J］.计算机工程与设计，2020，41（9）：2623-2629.（Lu Songjian，Si Weili，Han Juan，et al.Simplified particle swarm optimization algorithm for escape mean［J］.Computer Engineering and Design，2020，41（9）：2623-2629.）

［13］Seyedali M.SCA：A sine cosine algorithm for solving optimization problems［J］.Knowledge-Based Systems，2016，96：120-133.

［14］Hu Gang，Du Bo，Wang Xiaofeng，et al.An enhanced black widow optimization algorithm for feature selection［J］.Knowledge-Based Systems，2022，235，107638.

［15］Wang Jiquan，Bei Jinling，Song Haohao，et al.A whale optimization algorithm with combined mutation and removing similarity for global optimization and multilevel thresholding image segmentation［J］.Applied Soft Computing，2023，137：110130.

［16］賈鹤鸣，陈丽珍，力尚龙，等.透镜成像反向学习的精英池侏儒猫鼬优化算法［J］.计算机工程与应用，2023，59（24）：131-139.（Jia Heming，Chen Lizhen，Li Shanglong，et al.Elite pool dwarf mongoose optimization algorithm for lens imaging reverse learning［J］.Computer Engineering and Application，2023，59（24）：131-139.）

［17］柴岩，任生.多策略协同优化的改进HHO算法［J］.计算机应用研究，2022，39（12）：3658-3666，3677.（Chai Yan，Ren Sheng.Improved HHO algorithm for multi strategy collaborative optimization［J］.Application Research of Computers，2022，39（12）：3658-3666，3677.）

［18］Eberhart R，Kennedy J.A new optimizer using particle swarm theory ［C］//Proc of the 6th International Symposium on Micro Machine and Human Science.Piscataway，NJ：IEEE Press，1995：39-43.

［19］Trojovsky P，Dehghani M.Pelican optimization algorithm：a novel nature-inspired algorithm for engineering applications［J］.Sensors，2022，22（3）：855.

［20］李二超，高振磊.改进粒子速度和位置更新公式的粒子群优化算法［J］.南京师大学报：自然科学版，2022，45（1）：118-126.（Li Erchao，Gao Zhenlei.Particle swarm optimization algorithm for improving particle velocity and position update formula［J］.Journal of Nanjing Normal University：Natural Science Edition，2022，45（1）：118-126.）

［21］魏锋涛，张洋洋，黎俊宇，等.基于动态分级策略的改进正余弦算法［J］.系统工程与电子技术，2021，43（6）：1596-1605.（Wei Fengtao，Zhang Yangyang，Li Junyu，et al.Improved sine and cosine algorithm based on dynamic grading strategy［J］.Systems Enginee-ring and Electronic Technology，2021，43（6）：1596-1605.）