基于自适应Neville插值的野外移动机器人GPS定位

吴晗林,高兴华,刘晓飞,陈园林

(1.北华大学机械工程学院,吉林 吉林 132021;2.北京欣奕华数字科技有限公司,北京 100176)

机器人自主导航基于全球定位系统(GPS)及惯性导航、视觉感知等技术,因此,需要实时获取、处理和分析大量传感器数据[1-2],并快速反馈,以支持机器人做出准确决策、调整导航路径[3]。为了实现数据的高效处理,需要采用高性能硬件设备、先进算法和复杂的系统集成[4],而较高的系统成本限制了野外机器人在大规模工程实际中的应用、推广。

插值算法是一种通过已知数据点估算未知位置的数据处理技术,在数据填补、轨迹预测等领域受到关注[5-6]。其中,Neville插值法[7-9]是一种无须事先假设插值函数的多项式插值算法,在处理GPS信息等不均匀数据时具有独特优势。王晓明等[10]提出利用高次与低次Neville插值组合进行GPS插值,改善高阶次插值导致边缘区域插值精度出现的抖动;常远等[11]提出将滑动插值融合到Neville插值中进行GPS插值,根据时刻移动插值区域,复用插值结果,提高计算效率。以往研究实现了复杂算法优化,但需要大量计算资源,导致计算成本高昂。本文针对野外机器人在密林等野外环境中的实际应用情况,提出一种融合机器人状态的计算轻量化插值算法,以达到节约成本、提升可靠性和效率的目的。

1 移动机器人GPS定位

GPS是一类基于轨道卫星的无线电定位系统,由空间、地面控制和用户3部分构成[12],见图1。空间部分由一组人造卫星组成,用于发送位置和时间信号;用户部分是接收和处理卫星信号的终端设备,通过解算信号确定自身位置。接收机天线见图2。

图2 接收机天线Fig.2 Receiver antenna

定位过程:卫星1、2、3、4将各自位置信息P1、P2、P3、P4及时间戳发送到GPS接收机,将接收时间与数据包时间戳做差,获取位置信息传播的时间Ti,d1、d2、d3、d4为P1、P2、P3、P4到接收机的距离。由于数据包采用无线电波传输,传输速度c为3.0×108m/s,因此,数据传输模型可表示为

di=c×Ti,i=1,2,3,4 。

由于无线电波速度c的权重较高且与时间相关,故该定位过程对时间精度要求极高;信号在传播过程中可能会发生多次反射,使到达时间失真,即产生多路径效应,从而导致时间误差[13-14]。

2 Neville插值原理

插值是为了解决GPS定位过程中由于信号传输时延、遮挡等原因引起的数据不均匀、缺失和误差问题。通过在已知数据点间进行估计和填补,生成连续且平滑的位置信息,使得位置估计结果更加精确[15-16]。由于野外机器人定位须具备实时性等技术要求,由此,本研究采用Neville算法进行插值,此算法具有插值精度较高、计算效率高等优点。

Neville算法是一种用于插值多项式的算法,通过基于已知数据点的数值来估算处于两个已知数据点之间的未知数据点的值[17]。已知若干数据点a,则存在且仅存在1个次数≤a-1的多项式,且通过已知数据点。首先要确定插值数据点的个数n:

式中:(x0,y0)、(x1,y1)为需要插值的相邻数据点坐标。可解得一点(x0,1,y0,1)在(x0,y0)、(x1,y1)之间:

将插值点(x0,1,y0,1)与已知点(x0,y0)、(x1,y1)继续插值解得

(1)

(2)

化简式(1)和(2)得

通过迭代可得递归解

(3)

依据式(3)可得所需的n个插值点。

Neville插值算法可通过多次应用进一步提高插值结果的精度。对一组初始数据进行插值后,在该数据的特定区域内,再次运用插值算法,这样逐步逼近目标函数,可以得到更精细的插值结果,能够提高数据的精度和准确性。

3 Neville插值与定位精度分析

3.1 试验构建

为了研究Neville插值算法的效果及进行计算轻量化改进,搭建移动机器人平台进行野外试验。采用北天BT-300S模块作为平台的GPS接收器(图3),其具有多GNSS支持、高灵敏度、低功耗、小型化等特点,并且支持多种参考坐标系。搭建的野外移动机器人平台见图4。使用低压处理器工控机作为计算单元,以速度作为可调参数进行试验。

图3 北天BT-300S模块Fig.3 Beitian BT-300S module

图4 野外移动机器人平台 Fig.4 Field mobile robot platform

为了更好地对比试验结果,分别在速度为0.6、1.2、2.0 m/s下进行试验。试验区域见图5,面积为145 m×95 m,A点坐标为(126.564 693,43.920 621 8),B点坐标为(126.565 027,43.920 520 6),C点坐标为(126.564 964,43.920 539 6),D点坐标为(126.564 964 9,43.920 539 6),机器人每次都经过的对比点S的坐标为(126.564 698,43.920 635 9)。在图5红线框区域模拟野外工况开展试验。从相同点出发,每次移动轨迹尽可能相同并进行GPS数据接收,获取原始数据后进行处理,将经纬度变换为直观距离坐标[18]。使用MATLAB进行误差分析并绘制图像。

图5 定位数据试验区域 Fig.5 Locate the data experiment area

3.2 试验测试与分析

当机器人平台行走速度为0.6 m/s时,获取的GPS原始数据、插值后的GPS数据与机器人相应的实际运动路线见图6,三插值时3种速度下的数据散点图、对比点S与相应实际运动路线见图7。

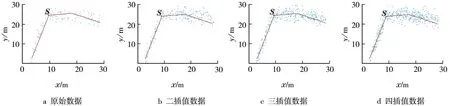
图6 速度为0.6 m/s时的数据效果Fig.6 Data renderings at a speed of 0.6 m/s

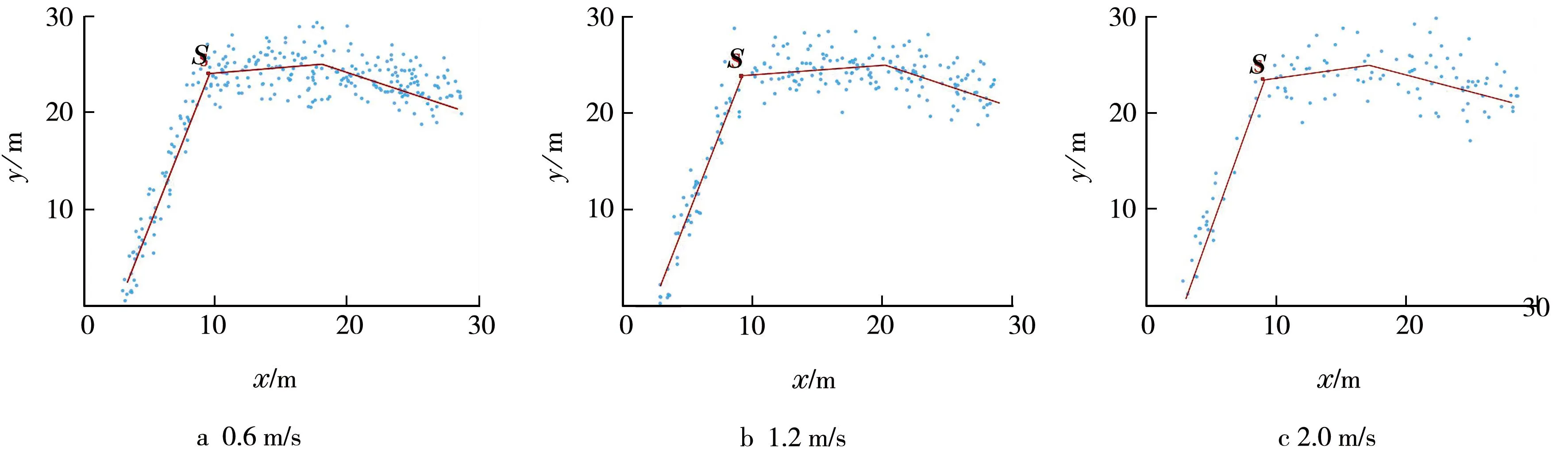
图7 不同速度三插值数据效果Fig.7 Effect of three interpolated data at different speeds

由图7可知:随着插值处理次数的增加,总数据点增加,定位精度也相应提高;当移动速度变大时,原始点减少,精度有所下降。继续对原始数据进行插值,在S处对误差与实际轨迹进行分析,结果见表1。

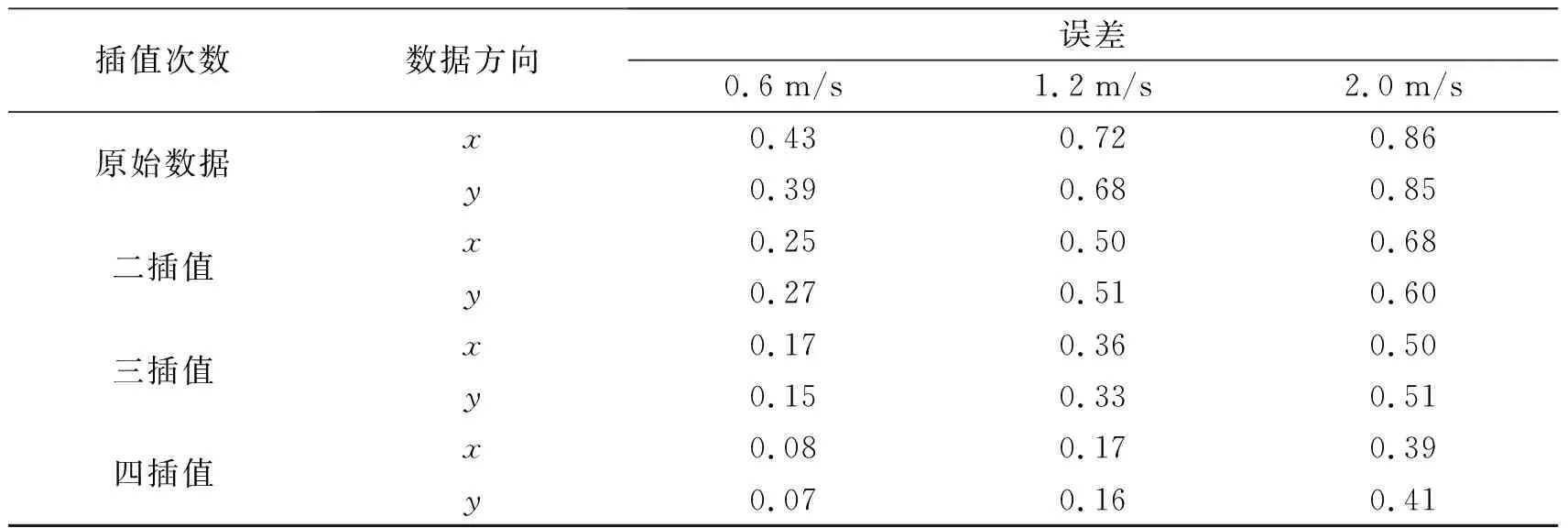
表1 数据处理误差

由表1可知:在2.0 m/s速度下,三插值处理效果较原始数据误差减少58.14%,即定位精度提升58.14%;随着插值处理次数的增多数据点增多,定位精度也相应提高;当机器人平台移动速度增大时,数据点变得稀疏,精度有所下降;随着插值处理次数的增加,数据量倍增,会导致平台计算压力陡增,影响到其他计算工作。

4 自适应Neville插值与状态信息融合控制

传统多次Neville插值算法在野外机器人定位中存在高成本、弱适应、低效率等问题:固定插值次数难以适应不同环境和场景需求,往往导致定位精度不足或计算开销过大;在复杂环境、高负载状态下计算速度过慢,影响实时性和响应性;当速度较快、姿态变化较大时,固定的数据填补不能满足精度要求。

为解决上述问题,本文提出一种自适应插值改进算法:当系统负载变高,环境变得平坦、开阔、障碍物较少,速度较慢和姿态变化较小时,降低插值次数,以减少计算开销并提高系统实时性;相反地,当系统负载较低,环境复杂性增加、存在障碍物,速度较快和姿态变化较大时,适度增加插值次数,以提高定位精度。通过动态调整插值次数,能够灵活适应不同情况,提高系统效率和性能。改进后的插值流程见图8。重复开展野外试验,结果显示:当速度为0.6 m/s和1.2 m/s时,插值精度不变;当速度为2.0 m/s时,插值精度较三次Neville插值提升了21.56%。

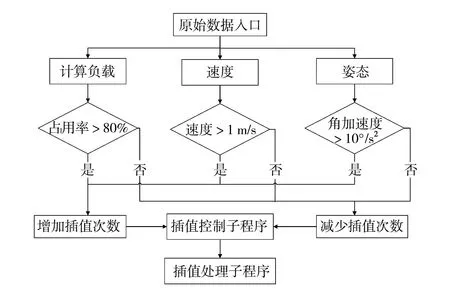
图8 插值流程Fig.8 Interpolation flow

从精度看,当传统算法部署在较低成本野外移动机器人上时,面对复杂野外场景,无法提供稳定的精度提升;根据机器人状态信息动态调整插值次数,可以提供应对复杂环境的动态精度提升。

从计算效率看,传统算法在高负载或简单环境下会产生不必要的计算开销,降低了系统的实时性;根据实时系统负载和环境情况动态调整插值次数,可以提高系统的计算效率和响应速度,使得机器人能够更快速、准确地响应环境变化,而不要求在野外移动机器人上持续堆叠计算单元。

5 小 结

本文通过多次Neville插值增补GPS数据,并开展了野外试验。结果显示:增加插值次数能够提升定位效果,在模拟野外工况下,三次Neville插值可使定位精度提高58.14%。同时,需要在插值次数和计算负担之间进行取舍,高次插值对精度提升存在边际效应,且计算开销较大;低次插值会出现适应性低、效率低等问题。本文提出的自适应插值改进算法,依据系统状态动态调整插值次数,可以节约成本、提升适应性和优化性能,为野外移动机器人定位提供一种有效的工程应用方案。未来可以进一步探索该方法的应用范围和优化策略,以推动野外机器人在实际工程中的应用。