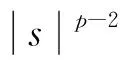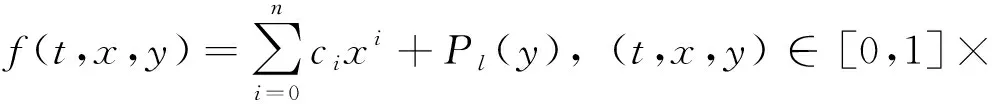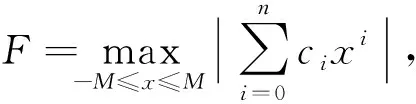一类带p-Laplace算子的非线性二阶m点共振边值问题解的存在性
2024-02-13刘美玉马锦然裴明鹤
刘美玉,马锦然,裴明鹤
(北华大学数学与统计学院,吉林 吉林 132013)
0 引 言
本文主要研究带p-Laplace算子的非线性二阶微分方程m点共振边值问题
(1)

近30年来,非局部边值问题已经成为微分方程定性理论中一个快速发展的研究领域。对这类问题的研究不仅受到理论兴趣的推动,而且还受到工程、物理和生命科学中的一些现象可以用这种方式进行建模事实的推动[1-2]。自1995年,GUPTA[3]首次研究了二阶m点共振边值问题解的存在性,非局部共振边值问题的研究取得了较大的进展[2,4-15]。注意到,以上文献所采用的研究方法主要有不动点指数理论[4,13]、迭合度理论[6,9,15]、Leray-Schauder连续性定理连同一些不动点定理[7-8,10,13]以及上下解方法等[11-12,14]。但有关带p-Laplace算子的二阶微分方程多点共振边值问题解的存在性研究较少见到[16-17]。
受上述文献以及文献[18-19]的启发,本文主要利用拓扑横截方法连同障碍带技巧,建立带p-Laplace算子的非线性二阶m点共振边值问题(1)的解的存在性结果。这里,我们想强调的是,本文的结果不仅是新的,而且对非线性项f不附加任何增长限制,同时非线性项f中的导数项的次数可以超过p次。
1 主要结果
在本文中,我们将使用如下条件:
(H1) 存在M>0,使得
xf(t,x,0)>0, ∀t∈[0,1],|x|>M。
(H2)存在常数Li,i=1,2,3,4满足L3 f(t,x,y)≤0, (t,x,y)∈[0,1]×[-M,M]×[L1,L2] , f(t,x,y)≥0, (t,x,y)∈[0,1]×[-M,M]×[L3,L4] 。 引理2[19-20]假设 则H(·,1)是本质的,从而H(1,1)在D内有不动点。 由连续函数的介值性,不难得到如下结果: 考虑边值问题族 (φp(x′) )′=λf(t,x,x′),t∈[0,1] , (2) (3) 其中λ∈(0,1] 。 引理4假设(H1)成立。则对边值问题族(2)-(3)的任意解x=x(t),都有 |x(t)|≤M,t∈[0,1] 。 (4) 证明:假设存在t0∈[0,1]使得|x(t0)|>M,不妨设x(t0)>M。令t1∈[0,1]使得 (5) 则根据引理3,我们可设t1∈[0,1), 从而x′(t1)=0。于是根据条件(H1),有 (φp(x′(t)))′|t=t1=λf(t1,x(t1),0)>0 , x′(t)>0,t∈(t1,t1+δ) 。 这与式(5)矛盾。证毕。 现在我们利用障碍带技巧得到x′(t)的先验界。 引理5假设(H1)和(H2)成立,则对边值问题族(2)-(3)的任意解x=x(t),有 (6) 证明:首先,定义两个集合S0和S1如下: S0={t∈[0,1]:L1 则S0和S1均是空集。事实上,假设S0≠∅,则存在t0∈S0,从而0 L1 (7) 并且 x′(t1)≤x′(t)≤x′(t2),t∈[t1,t2] , 从而[t1,t2]⊂S0。注意到,由引理4,|x(t)|≤M,t∈[0,1],所以根据(H2),有 (φp(x′(t)))′=λf(t,x(t),x′(t))≤0,t∈[t1,t2] 。 x′(t2)≤x′(t1) , 这与式(7)矛盾。这表明S0=∅。类似可证S1=∅。于是由边界条件(3)以及x′(t)在[0,1]上的连续性,我们可知式(6)成立。证毕。 现在,我们定义Banach空间X=C1[0,1]×具有如下范数: 设 U={(x,r)∈X:x(0)=0,r∈} 以及 则U是X的闭凸子集,并且D是U的相对开子集。 则F是本质的。 则易证H(x,r,λ)是紧算子。显然H(x,r,1)=F(x,r),H(x,r,0)=(0,0)∈D, 所以根据引理1,H(x,r,0)是本质的。 现在我们证明 H(x,r,λ)≠(x,r), (x,r)∈∂D,λ∈[0,1] 。 (8) 显然,当(x,r)∈∂D时,H(x,r,0)≠(x,r)。假设存在(x0,r0)∈∂D以及λ0∈(0,1],使得H(x0,r0,λ0)=(x0,r0),则x0=0以及 从而 因此,根据(H1)可推得|r0|≤M, 从而(x0,r0)∈D,这与(x0,r0)∈∂D且D为开集矛盾。这表明式(8)成立。于是根据引理2,F(·,·)=H(·,·,1)是本质的。 证毕。 定理1假设(H1)和(H2)成立,则边值问题(1)至少存在一个解x=x(t)满足式(4)和式(6)。 其中符号“*”表示向量的转置。利用Arzelà-Ascoli定理容易证明算子G是紧算子。 假设(x1,r1)是G(·,·,1)的一个不动点,则 以及 于是 以及 因此 令x2(t)=x1(t)+r1,t∈[0,1]。易见,x2是问题(1)的解,并且根据引理4和引理5可知x2满足式(4)和式(6)。因此,为了证明问题(1)的满足式(4)和式(6)的解的存在性,只需证明算子G(·,·,1)具有不动点。注意到,G(·,·,0)=F(·,·),并且由引理6可知F是本质的,所以为了得到G(·,·,1)的不动点的存在性,只需验证引理2的条件(ii)成立。假设存在(x0,r0)∈∂D,λ0∈[0,1],使得G(x0,r0,λ0)=(x0,r0),则由引理6知,λ0≠0,所以λ0∈(0,1]。于是 以及 (9) 因此 特别地,有 x′0(0)=0 。 即 兹令x(t)=x0(t)+r0,t∈[0,1]。 则易见,x是边值问题(2)-(3)当λ=λ0时的解。因此,根据引理4以及引理5,有 ‖x0+r0‖∞=‖x‖∞≤M, (10) 以及 注意到,x0(0)=0, 所以由式(10)知|r0|≤M,从而 ‖x0‖∞≤M+|r0|≤2M<2M+1 。 综上可得,(x0,r0)∈D,这与(x0,r0)∈∂D且D为开集矛盾。故引理2的条件(ii)成立。证毕。 例1考虑带p-Laplace算子的二阶m点共振边值问题 (11) 令 则f在[0,1]×2上连续。再令ri(i=1,2,…,ν,ν≤n)是n次多项式的所有实根。记 M=max{|r1|,|r2|,…,|rν|}>0 。 则当t∈[0,1],|x|>M时,有 Pl(y)-F≤f(t,x,y)≤Pl(y)+F。 于是若sup{Pl(y)-F:y<0}>0且inf{Pl(y)+F:y>0}<0,则(H2)成立,从而由定理1,带p-Laplace算子的二阶m点共振边值问题(11)至少存在一个非平凡解。




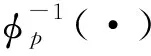
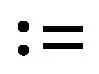
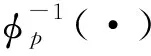
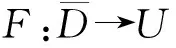
2 应用举例