基于BB步长的近端随机递归动量算法

钱玉香,赵 勇,杨 帆

(重庆交通大学数学与统计学院,重庆 400074)

0 引 言

本文考虑如下的复合优化问题:

minx∈dΨ(x)=f(x)+g(x) ,

(1)

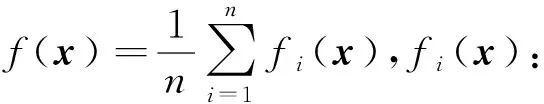
为了有效求解复合优化问题(1),国内外学者提出了诸多高效的算法。FUKUSHIMA等[3]提出的近端梯度下降(ProxGD)算法是解决该类问题的一种经典算法,其主要迭代步骤为:

xt=proxηg(xt-1-η∇f(xt-1)) ,

其中η>0为步长。当样本数据非常大时,ProxGD算法每一步的计算成本都非常昂贵。因此,GHADIMI[4]用随机梯度代替全梯度,提出了近端随机梯度下降(ProxSGD)算法。但随机采样的方式引入了随机误差,限制了该算法的收敛速度。XIAO和ZHANG[5]提出了一种近端随机方差缩减(ProxSVRG)算法来提高ProxSGD算法的收敛速度。NGUYEN等[6]提出了一种近端随机递归梯度(ProxSARAH)算法并达到了相同的效果。此外,CUTKOSKY和ORABONA[7]提出了一种随机递归动量(STORM)算法求解非凸优化问题,该算法结合动量递归技术和自适应步长来实现方差缩减的效果。WANG和WEN[8]将动量递归技术与近端梯度算法结合,提出了求解非凸非光滑复合优化问题的近端随机递归动量(ProxSTORM)算法。

众所周知,步长是影响梯度类算法收敛速度的一个关键因素。在大多数随机算法中,通常采用两种步长策略:1)固定步长,需要手动调整参数以达到最佳性能;2)衰减步长,但是当迭代接近最小值时,可能会降低算法性能。为了解决这一问题,TAN等[9]将Barzilai-Borwein(BB)步长[10]应用到SVRG中,提出了SVRG-BB 算法求解强凸优化问题,并且通过数值实验验证了SVRG-BB算法具有良好的算法性能,可以达到与使用最佳步长的SVRG算法相同甚至更好的效果。YANG等[11]将BB 步长与mS2GD算法结合,提出mS2GD-BB算法,并证明了mS2GD-BB算法对于非光滑强凸目标函数在期望意义下是线性收敛的。为了进一步提高小批量算法的收敛速度,YANG等[12]将改进的BB步长(RBB)与Acc-ProxSVRG算法结合,提出Acc-ProxSVRG-RBB算法求解强凸优化问题,BB步长的使用解决了参数调优的困难并达到了与这些算法使用最佳步长时相同甚至更好的收敛速度。然而,当目标函数非凸时,使用BB步长或RBB步长导致分母可能接近零,甚至为负。故上述算法不能有效求解非凸问题。因此,MA等[13]提出SVRG-SBB算法求解随机非凸嵌入问题,该算法将SBB步长和SVRG算法结合并通过数值实验验证了算法的有效性。但是计算步长时,SBB步长使用全梯度,导致计算成本较昂贵。

受文献[11-13]的启发,本文将改进的SBB步长与ProxSTORM算法结合,提出ProxSTORM-BB算法求解非凸非光滑复合优化问题。然后,在合适的假设条件下证明了算法的收敛性。最后,通过数值实验验证了算法的有效性。

1 基本符号与定义

定义1[14]设g:d→d∪{∞}是适定的下半连续凸函数,对x∈domg,定义

为g在x处的次微分。

定义2[15]定义广义梯度为

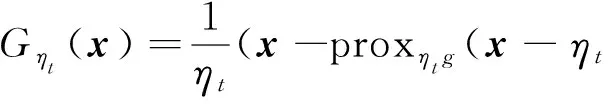
其中,ηt表示第t次迭代的步长。当g≡0时,Gηt(x)=∇f(x)。

定义3[16]对于一个凸函数g,定义它的邻近算子为

假设1 设∇fi(x),i∈[n]是利普希茨(Lipschitz)连续的,其中利普希茨常数L>0,即

‖∇fi(y)-∇fi(x)‖≤L‖y-x‖, ∀x、y∈d。

假设2 存在σ∈[0,+∞),使得

E[‖∇fi(x)-f(x)‖2]≤σ2, ∀x∈d,i∈[n] 。

2 ProxSTORM-BB算法

经典的BB步长[10]为

但是使用全梯度导致计算成本非常昂贵,故利用随机梯度代替全梯度,有

其中γ为正常数。受到BB步长成功应用于随机优化算法的启发[11-13],将改进的BB步长与近端随机递归动量(ProxSTORM)算法相结合,提出了ProxSTORM-BB算法求解问题(1)。具体算法框架如下:

3 收敛性分析

下面来分析ProxSTORM-BB算法的收敛性,首先介绍本节将用到的引理。

引理1假设1～2成立,{vt}是由算法1产生的,其中a∈(0,1),则

E[‖vt-∇f(xt)‖2]≤(1-a)2E[‖vt-1-∇f(xt-1)‖2]

基于上述引理,建立ProxSTORM-BB算法的收敛性。

证明:由xt+1的定义和g的凸性可得,对∀y∈d,有

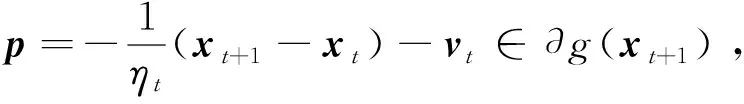
令y=proxηtg(xt-ηt∇f(xt)),由近端算子的最优性条件[16]可得

即

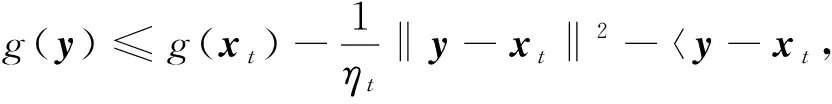
由于∇f是Lipschitz连续的,则

再结合Ψ(x)和Gηt(x)的定义并取全期望, 有

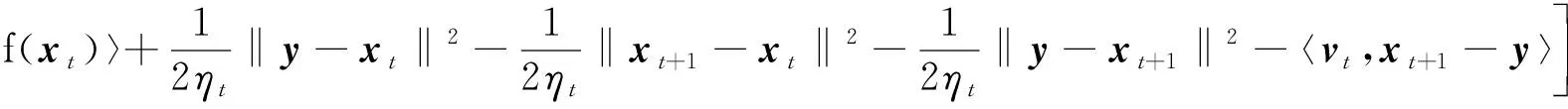
其中最后一步不等式由2ab≤a2+b2和Gηt(x)的定义可得。

接下来分析ηt的取值范围

结合假设2可知,

下面,我们构造一个Lyapunov辅助函数

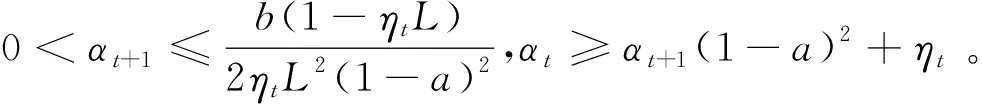
其中ξ>L+γ。由R(xt+1)的定义可得

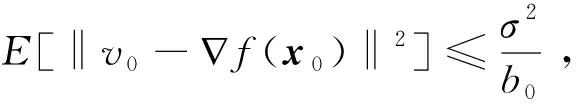
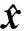
证毕。

4 数值实验

本节通过数值实验来验证ProxSTORM-BB算法的有效性。我们主要考虑了2个例子,所有的实验均是在MATLAB 2019a,Windows10系统下进行的。计算机基本参数为AMD Ryzen 5 5500U @2.10 GHz 和16 GB内存。其中“loss”代表求解目标函数所得的残差损失(目标函数值减去最优值),“CPU time”表示程序运行的时间,单位为秒。在实验中固定批量大小b=20,并且选择CINA.test(n=3 206;d=132)和a9a.test(n=16 281;d=122)为数据集。

例1[17]考虑如下非凸非光滑复合优化问题:

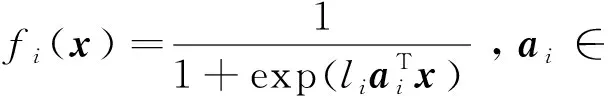
首先,为了验证ProxSTORM-BB算法的有效性,将ProxSTORM-BB算法和使用固定步长的ProxSTORM算法进行对比。同时为了使实验结果更加准确,其他参数(小批量b和动量参数a)的设定均相同,并且在实验中两个算法的初始步长均选取η0=0.015。实验结果如图 1所示。

下面,验证初始步长对ProxSTORM-BB算法的影响。在保证其他参数相同的情况下,选取了3个相差较大的初始步长:η0=0.009,η0=0.015和η0=0.1,在不同的数据集上进行实验。 实验结果如图2所示。

最后,为了比较ProxSTORM-BB算法与其他算法的性能,将ProxSTORM-BB算法、 ProxSGD算法和ProxSVRG算法在不同的数据集上进行了对比。为了使结果更加准确,在ProxSVRG算法中,选取小批量b=20。实验结果如图3所示。

例2考虑如下非凸非光滑复合优化问题:

与例1类似,为了验证ProxSTORM-BB算法的有效性,将ProxSTORM-BB算法和使用固定步长的ProxSTORM算法进行对比。实验结果如图4所示。

下面,同样在保证其他参数相同情况下,选取了3个相差较大的初始步长:η0=0.009,η0=0.015和η0=0.1,在不同的数据集上进行实验来验证初始步长对ProxSTORM-BB算法的影响。实验结果如图 5所示。

最后,将ProxSTORM-BB算法、ProxSGD算法和ProxSVRG算法在不同的数据集上进行了对比。实验结果如图6所示。

实验结果:

1)在图1和图 4中,x轴代表CPU时间,y轴代表求解目标函数所得的残差损失。由图1和图4可知,对于例1和例2,在不同的数据集上,ProxSTORM-BB算法和使用固定步长的ProxSTORM算法相比,都达到了相同甚至更好的效果。在相同的CPU时间下,ProxSTORM-BB算法使相应问题的目标函数值下降更快,有更小的残差损失,这验证了我们所提出算法的有效性。

图1 BB步长与固定步长对比Fig.1 Comparison of BB step size and fixed step size

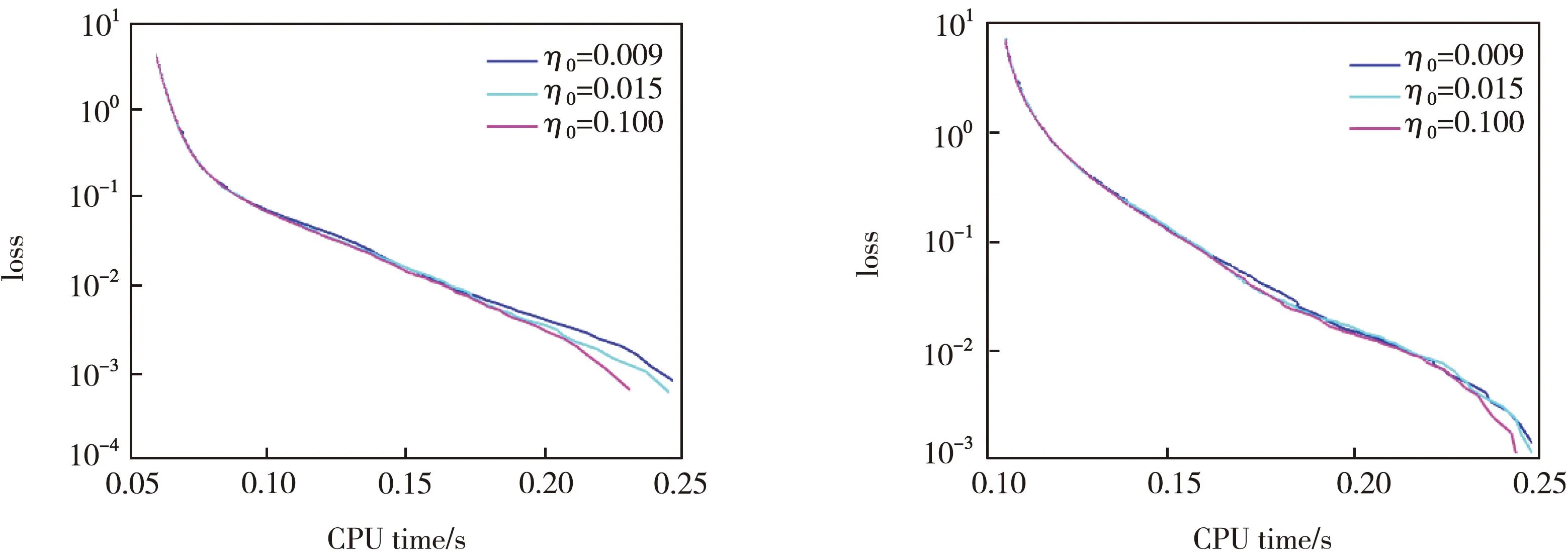
图2 不同初始步长对比Fig.2 Comparison of different initial steps

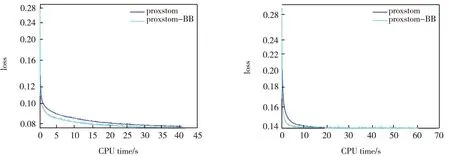
图4 BB步长与固定步长对比Fig.4 Comparison of BB step size and fixed step size

2)由图2和图5可知,针对例1和例2,在数据集CINA上,不同的初始步长对ProxSTORM-BB算法的影响很小;在数据集a9a上,不同的初始步长对ProxSTORM-BB算法的影响几乎可以忽略。因此,ProxSTORM-BB算法对于初始步长的选取具有鲁棒性。

图5 不同初始步长对比Fig.5 Comparison of different initial steps

3)在图3和图6中,x轴代表CPU时间,y轴代表求解目标函数所得的残差损失。由图3和图6可知,对于例1和例2,在不同的数据集上,ProxSTORM-BB算法都使相应问题的目标函数值下降更快。在相同的CPU时间下,有更小的残差损失,实现了更快的收敛速度。因此,ProxSTORM-BB算法具有更好的性能。

图6 与其他算法对比Fig.6 Comparison with other algorithms