混合策略改进的粒子群算法

朱茂桃,刘 欢,吴佘胤,商高高

(江苏大学 汽车与交通工程学院, 江苏 镇江 212013)

0 引言

粒子群算法(particle swarm optimization,PSO)是Kennedy等[1]在1995年提出的,因其结构简单,参数少且易于实现,受到众多学者的研究,并被广泛运用于交通、物流、特征选择等多个领域[2-3]。但粒子群算法本身也存在收敛精度低、速度慢、易早熟等缺点。

目前,众多学者提出了不同策略来改进PSO算法。钱晓宇等[4]提出基于局部搜索的反向学习竞争粒子群优化算法,将初始种群随机分成四类,将类中粒子按照适应值大小进行排序并执行相应的搜索策略,丰富了种群的多样性,在算法后期各粒子相互竞争,增强了粒子跳出局部最优的能力,在高维测试中也表现出较好的性能,但所需迭代的次数较多。李国森等[5]提出基于邻域驱动的粒子群算法,引入邻域驱动策略将粒子划分到不同的邻域中,通过邻域间的信息交流,自适应更新粒子的位置,较好地平衡了全局搜索能力与局部勘探的能力,但没有验证算法在高维度上的性能。陈曦等[6]引入莱维飞行和黄金正弦公式对粒子的速度和位置进行更新,增大了粒子的搜索范围,在一定程度上提升了算法的收敛速度和精度,但跳出局部最优能力仍有提高的空间。刘清等[7]在线性递减惯重粒子群算法的基础上,将目标函数的梯度信息以扰动的形式添加到速度更新公式中,粒子进行迭代时随机选择速度更新方式,在不影响收敛精度的同时提高了算法的速率,但无法收敛到最优解。于海波等[8]提出带偏向性轮盘赌的多算子协同优化算法,根据轮盘赌策略对种群执行不同的搜索机制,将每次迭代后的信息进行交流汇总并对全局最优施加高斯变异,虽然增强了算法的收敛性能,但在求解多极值问题时效果欠佳。

为进一步提升PSO算法的性能,本文中提出了一种改进的粒子群算法。将精英反向学习策略[9]与Circle映射[10]引入到种群初始化,提升种群质量同时扩大搜索范围;通过改变粒子速度更新公式,更好地平衡PSO算法的全局探索与局部勘探能力;结合基于自适应t分布的变异策略,进一步增强了全局探索和跳出局部极值能力。通过15个测试函数表明,改进的PSO算法在高维和低维函数上具有很强的寻优能力与稳定性。

1 相关算法的介绍

1.1 粒子群算法

粒子群算法是一种基于群体智能的优化算法[11],最初起源于对鱼群和鸟群等自然现象的模拟。粒子在搜索过程中,通过相互间的信息交流不断改变自身的速度与位置,最终聚集到最优解附近。粒子速度更新公式如式(1)所示,位置更新如式(2)所示。

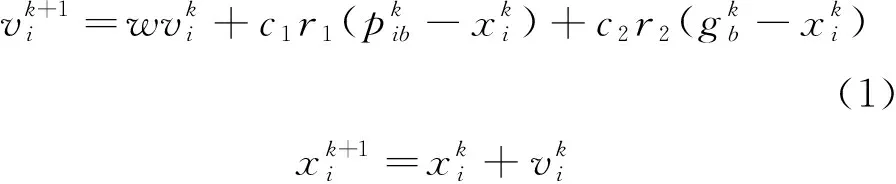
(2)

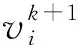
1.2 黑寡妇优化算法(BWOA)

蜘蛛在网中的运动模型有线性与螺旋2种,如图1所示。表达式见式(3),Xi(t+1)为更新后的蜘蛛位置,Xbest为当前最好的蜘蛛位置,m为[0.4,0.9]的随机数,β为[0,1]的随机数,Xr1(t)为随机选择的第r1个蜘蛛,Xi(t)为当前蜘蛛的位置。

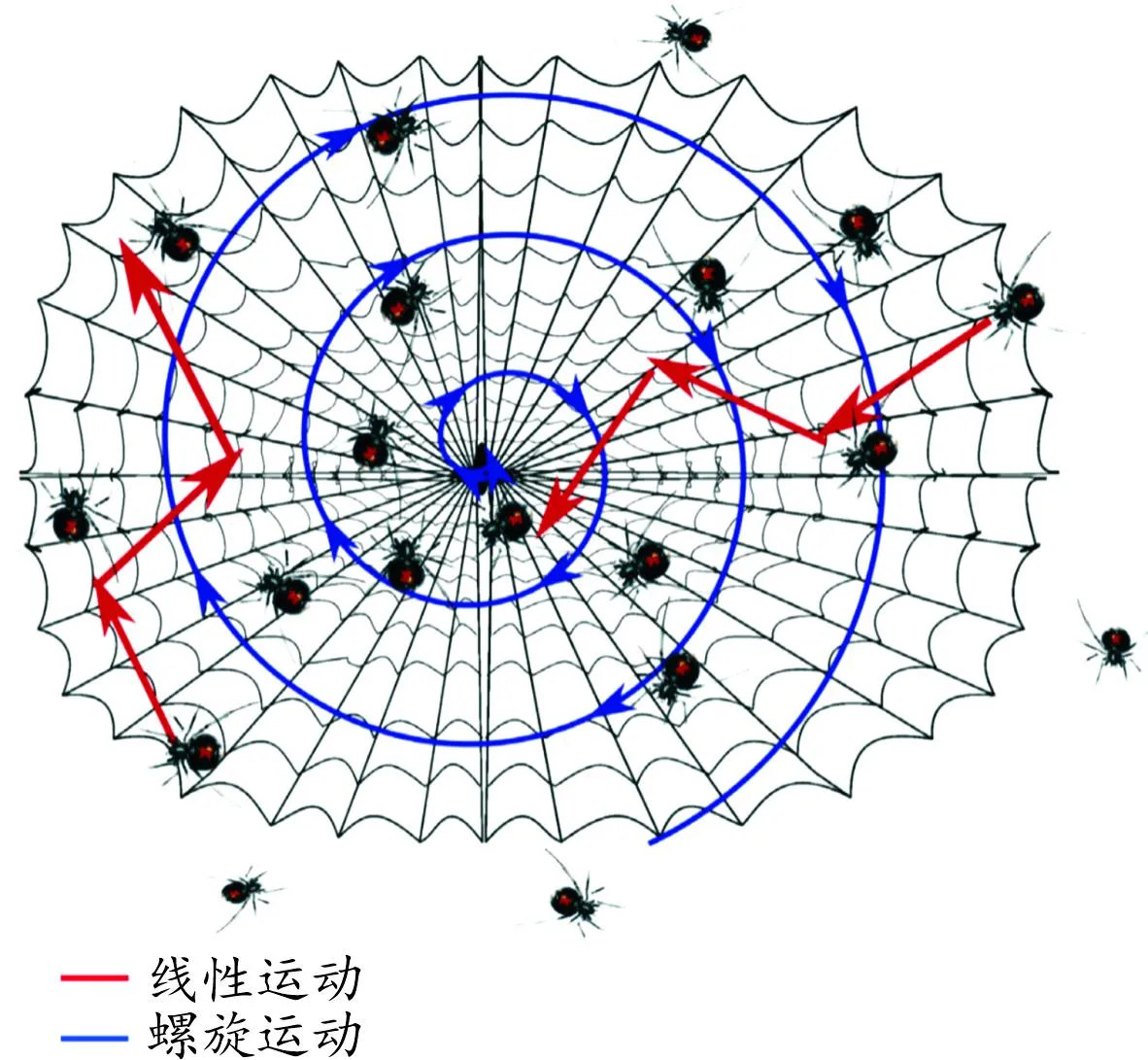
图1 线性(linear movement)与螺旋(spiral movement)运动

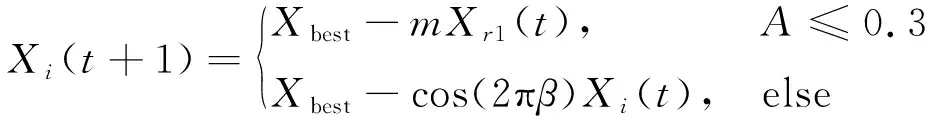
(3)

定义信息素为

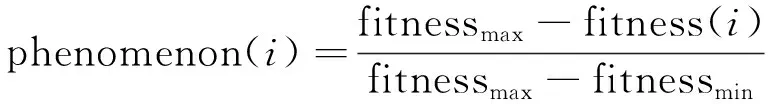
(4)

式中: fitnessmax与fitnessmin是最好与最差的适应值;fitness(i)是第i个蜘蛛的适应值。信息素低的蜘蛛会被替换:

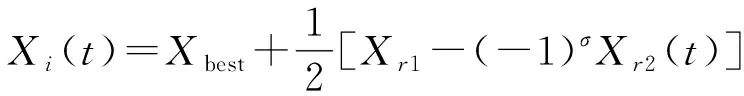
(5)

式中:Xi(t)为信息素低的蜘蛛的位置;r1、r2为1到种群数量N之间随机的2个不相等的数;σ为二进制数{0,1}。

1.3 反向学习

受机器学习中反向学习概念的启发,Tizhoosh[13]于2005年提出反向学习算法。精英反向学习算法[14]的核心思想为:在种群进行搜索时,同时搜索当前解与其动态反向解,并将较好的解保留到下一代。

反向解的定义:设X=(x1,x2,…,xD)为D维空间上的一点,xi∈[li,ui],则其反向解为

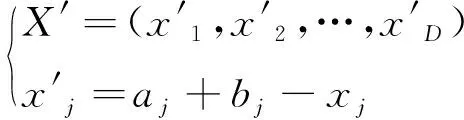
(6)

动态反向解的定义:设X=(x1,x2,…,xD)为D维空间上的一点,则其动态反向解为

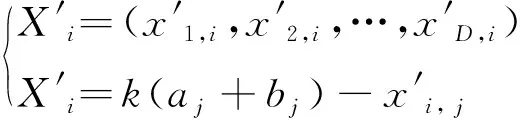
(7)

式中:xi∈[li,ui],k∈(0,1)。

2 本文改进的算法

2.1 融合Circle映射与精英反向学习的种群初始化

混沌映射因其具有遍历性、规律性等特点[14],常被用于种群的初始化中,但群数量较低时,无法覆盖到较好的点,使得算法的搜索效率降低。因此,本文将精英反向学习策略融入到混沌映射中,充分利用混沌映射遍历性的特性,在初始化种群时,同时搜索混沌映射解与其动态反向解,进一步扩大算法的搜索范围,选择较优的解作为初始种群,避免盲目性,提升初始种群的质量。引入Circle映射,如式(8)所示。

式中:xi+1, j为第i+1个粒子的第j维上的混沌序列值;xi, j为第i个粒子在第j维上的序列值。

使用融合Circle映射与精英反向学习策略,Circle映射对数量为20的种群分别在100维及200维上进行初始化,在Sphere函数上进行30次测试,并设置最大迭代次数为100。实验统计结果见表1,收敛曲线如图2所示,结合图表可以看出使用融合Circle映射与精英反向学习策略进行种群初始化的PSO收敛速度最快,且精度最高,这是因为引入了精英反向学习的Circle映射使得种群在2个空间上同时进行搜索,可以扩大种群的搜索范围,结合精英淘汰制提升了初始化种群的质量,从而提升算法的搜索效率。

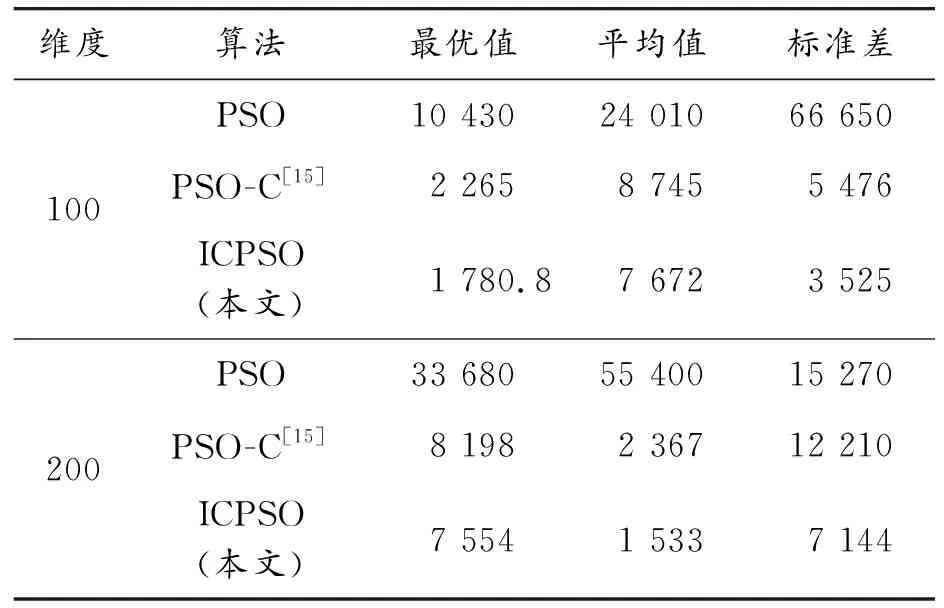
表1 Sphere函数测试结果

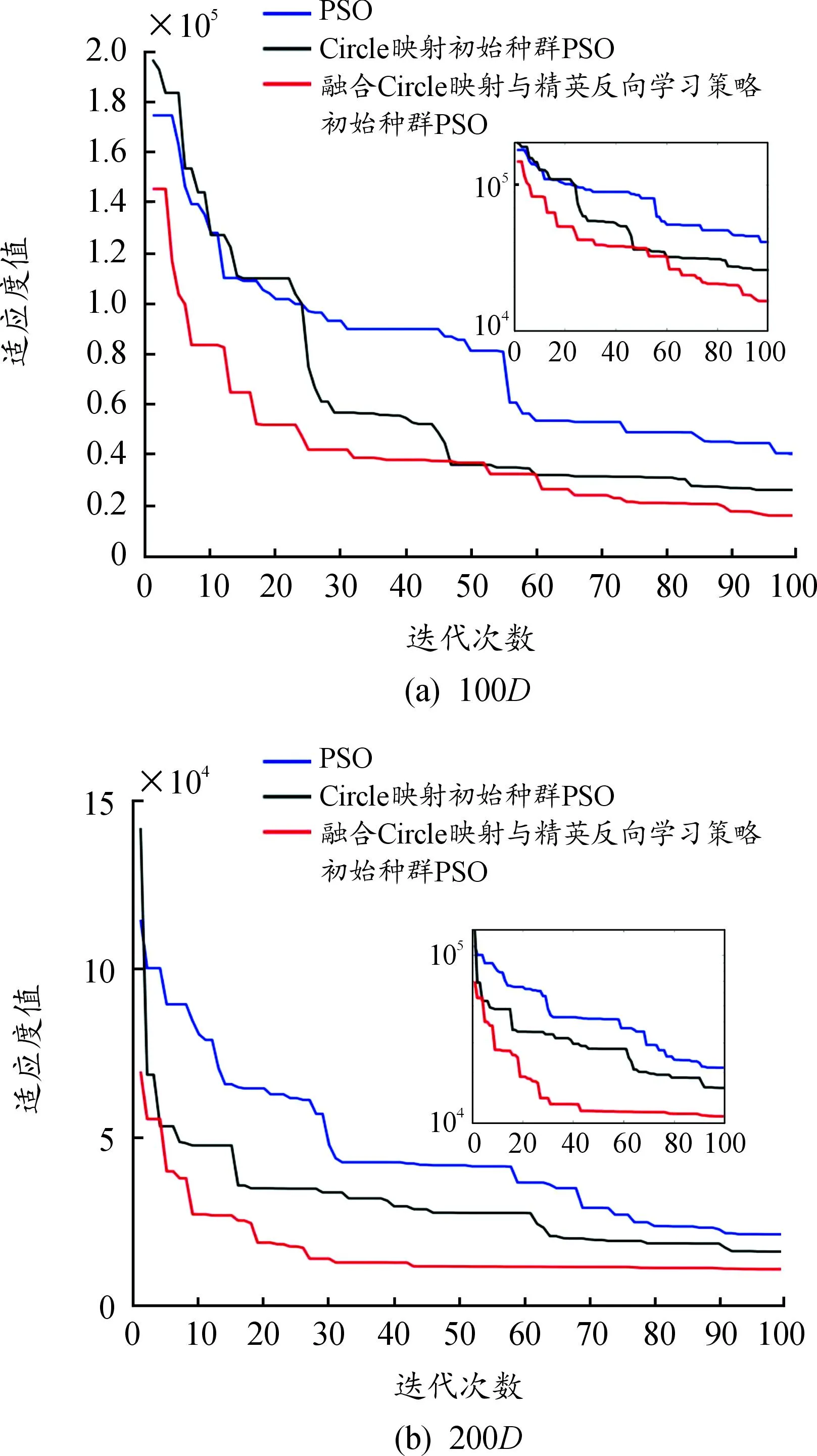
图2 不同策略初始化种群时Sphere收敛曲线(30D)

种群初始化的步骤如下。

步骤1：随机初始化第一个粒子混沌序列值x1, j,j=1,2,…,D,D为种群的维数。

步骤2：依次计算每个粒子的序列值,如式(8)。

步骤3：生成种群动态反向解,如式(7)。

步骤4：计算粒子的初始化位置,如式(9),其中,Xlj、Xuj分别为粒子在第j维的上下界。

步骤5：选取适应度值较好的粒子作为初始化种群。

Xi, j=Xlj+(Xuj-Xlj)×xi, j

(9)

2.2 改进惯性权重与学习因子

惯性权重可以影响粒子群算法的全局搜索能力与局部勘探能力,较大时利于全局搜索,此时种群的搜索范围扩大,较小时利于局部勘探,此时粒子在当前点附近进行精细搜寻,算法跳出局部极值的能力增强。提出一种非线性递减的惯性权重策略:

w=wmax-(wmax-wmin)·

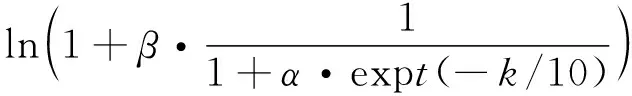
(10)

式中:wmax、wmin分别为惯性权重最大值与最小值;k为当前迭代次数;α、β为系数。

对学习因子改进的公式如式(11)所示。cmax、cmin分别为惯性权重最大值与最小值;k、K分别为当前迭代次数与最大迭代次数;c1为个体学习因子,c2为社会学习因子,前期应使c1大一些,c2小一些,粒子多向自身进行学习,提升算法的全局探索能力,后期则刚好相反,多向全局历史最优学习,增强局部勘探能力。

(11)

选取Sphere和Griewank作为测试函数(见表2),设置种群数为50,最大迭代次数为100,在每个测试函数上进行30次测试,将本节改进算法(PSO-IW)与其他3种相关粒子群算法进行对比,收敛曲线如图3所示,实验统计结果如表3所示,参数设置如表4所示。

表2 基准测试函数

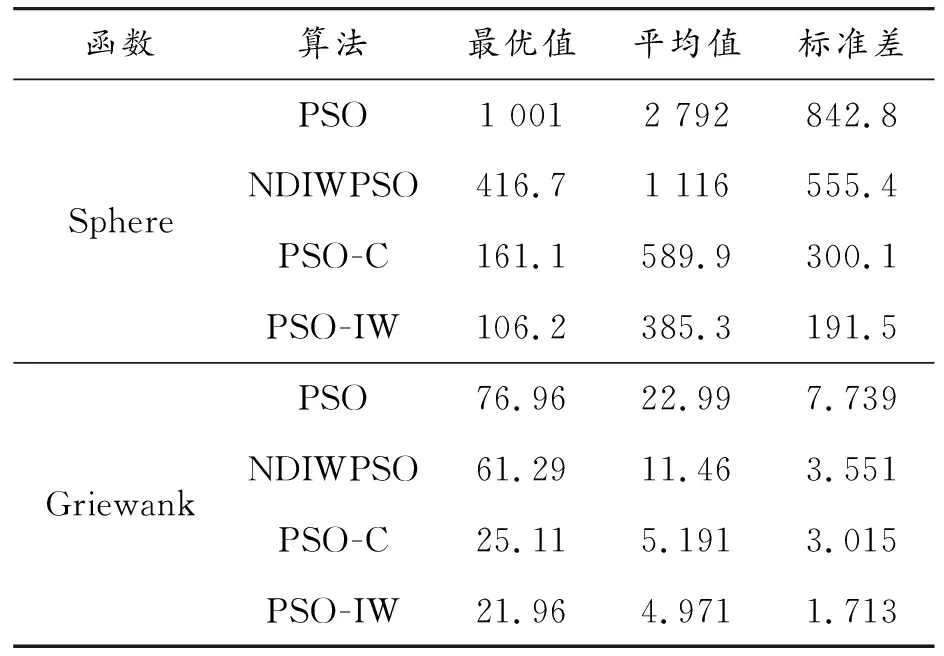
表3 Sphere与Griewank函数测试表

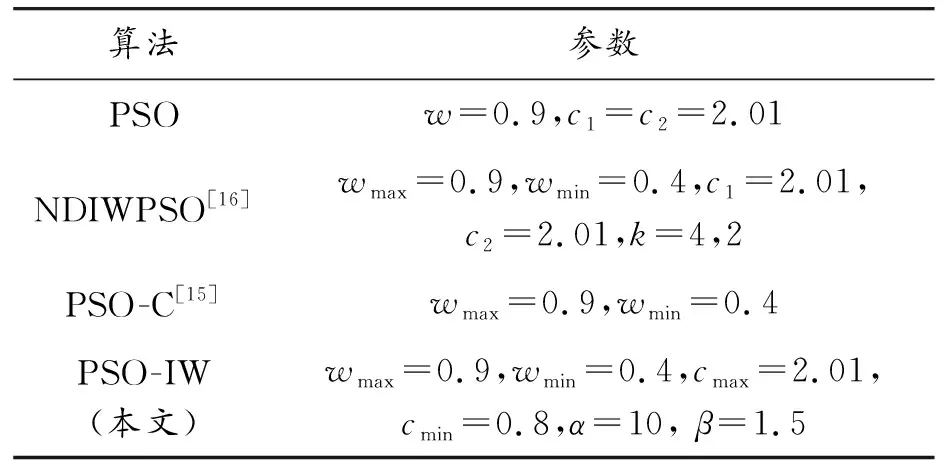
表4 相关粒子群参数设置

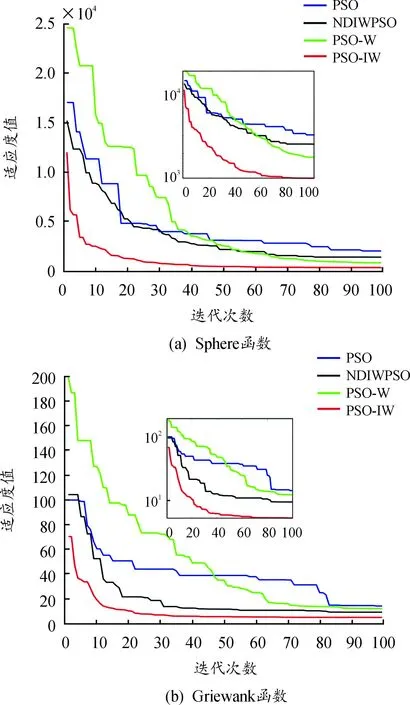
图3 不同策略改进PSO时收敛曲线(30D)

4种算法均没有找到最优解,但PSO-IW在单峰和多峰上函数上都具有较快的收敛速度,同时可以注意到PSO-IW不仅在2个测试函数上均找到了最小精度的解,同时平均值、标准差均比其他3种算法少,这说明PSO-IW有着稳定的寻优能力。

2.3 引入蜘蛛移动策略

在标准PSO中,粒子通过不断朝着自身历史最优与全局最优的方向飞行来寻找最优解,粒子在飞行过程中找到某个局部最优点后难以摆脱,且可能会吸引其他粒子向其周围聚集,使种群陷入局部最优,同时随着其他粒子越来越接近全局最优粒子,种群多样性降低,收敛速度会大幅下降甚至发生进化停滞。

受BWOA位置更新公式的启发,对粒子的速度更新公式进行调整。并引入概率p∈[0,1],当p<0.3时,采用式(12)更新速度,否则采用式(13)更新粒子速度,其中m为[0.4,0.9]的随机数,β为[0,1]的随机数,(-1)σ为方向控制因子,σ为二进制数{0,1}。

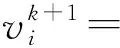
(12)

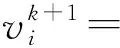
(13)

将改进速度更新公式后的PSO(PSO-IC)与标准PSO分别在单峰测试函数Sphere和多峰测试函数Griewank上进行30次测试,种群数设置为50,最大迭代次数为100,收敛曲线如图4所示,实验统计结果如表5所示。可以看出,引入蜘蛛策略后的PSO算法具有更快的收敛速度,这是因为与标准PSO相比,改进后的PSO算法中粒子以线性与螺旋形2种方式来搜寻最优解,扩大了算法的搜索范围,丰富了种群多样性,进而加快收敛速度,在2个测试函数上,引入蜘蛛策略后的PSO算法虽然都有过一段时间的停滞,但均跳出了局部最优并找到了最优解,这是通过引入方向控制因子,粒子以线形和螺旋形2种方式围绕粒子个体最优位置和全局最优位置进行震荡式来回搜索,不仅进一步丰富粒子飞行方向的多样性,还极大地增强了粒子跳出局部最优的能力。通过对比可以得出,无论在单峰还是多峰函数上,引入蜘蛛移动策略改进的PSO有着很强的适用性。

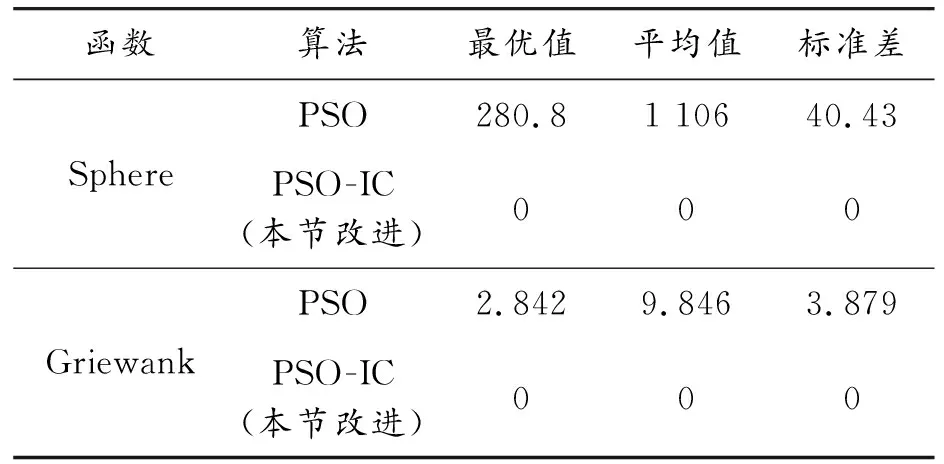
表5 Sphere与Griewank函数测试

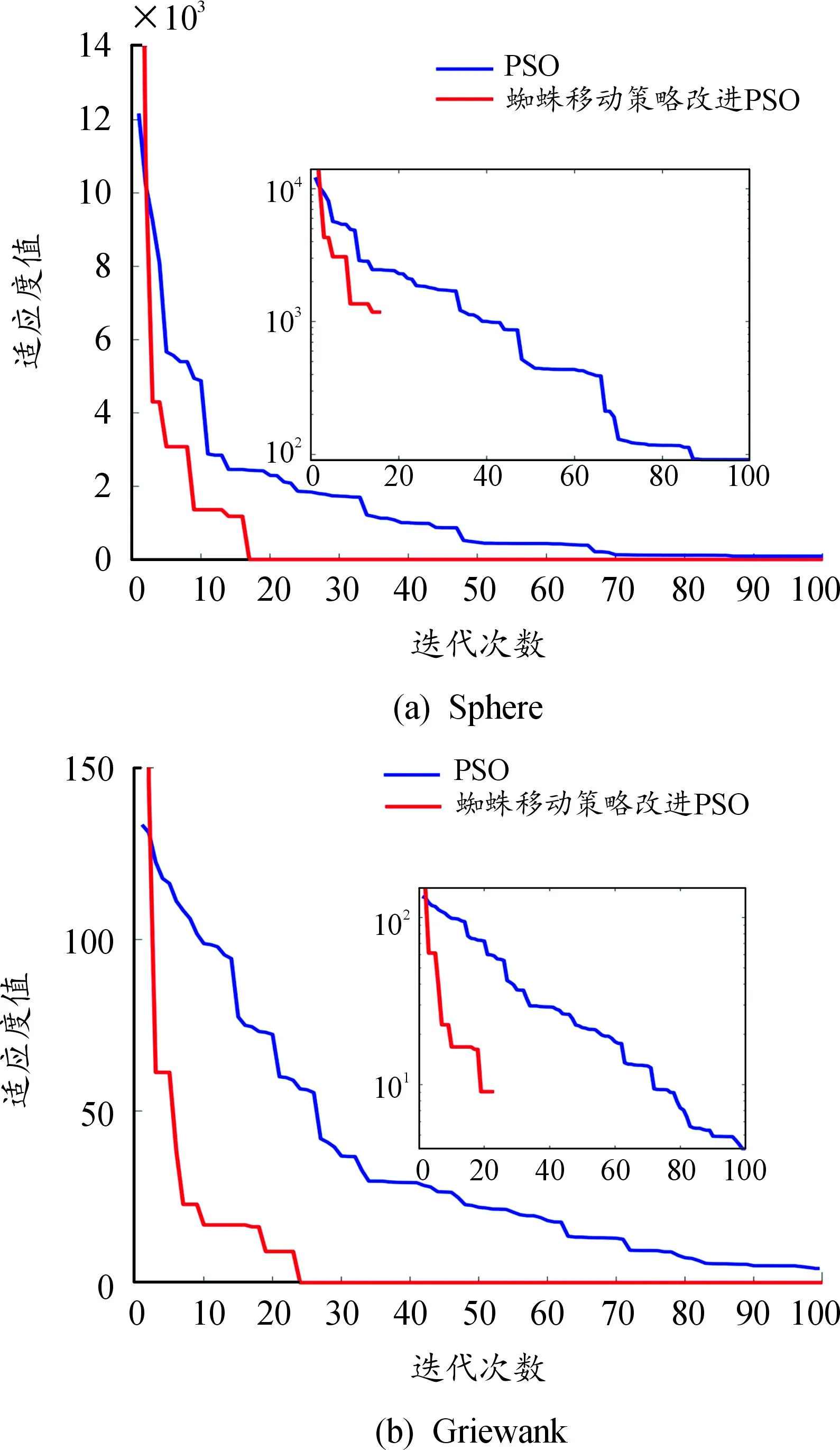
图4 蜘蛛移动策略改进PSO曲线(30D)

再结合改进的惯性权重与学习因子,更好地平衡PSO算法的全局搜索能力与局部勘探的能力。

2.4 自适应t变异策略

t分布又称学生分布[17],自由度n为其唯一参数,当n向正无穷发生变化时,其形态也由平缓变成陡峭。t(n=1)=c(0,1),t(n→∞)=N(0,1),其中N(0,1)为高斯分布,c(0,1)柯西分布。如图5所示,将迭代次数作为t分布变异的自由度,可以很好地结合高斯变异与柯西变异的优点,在算法迭代前期,曲线靠近柯西分布,可以增大算法的搜索空间,在迭代后期,曲线向高斯分布靠拢,此时有利于算法的局部开发。t变异公式为

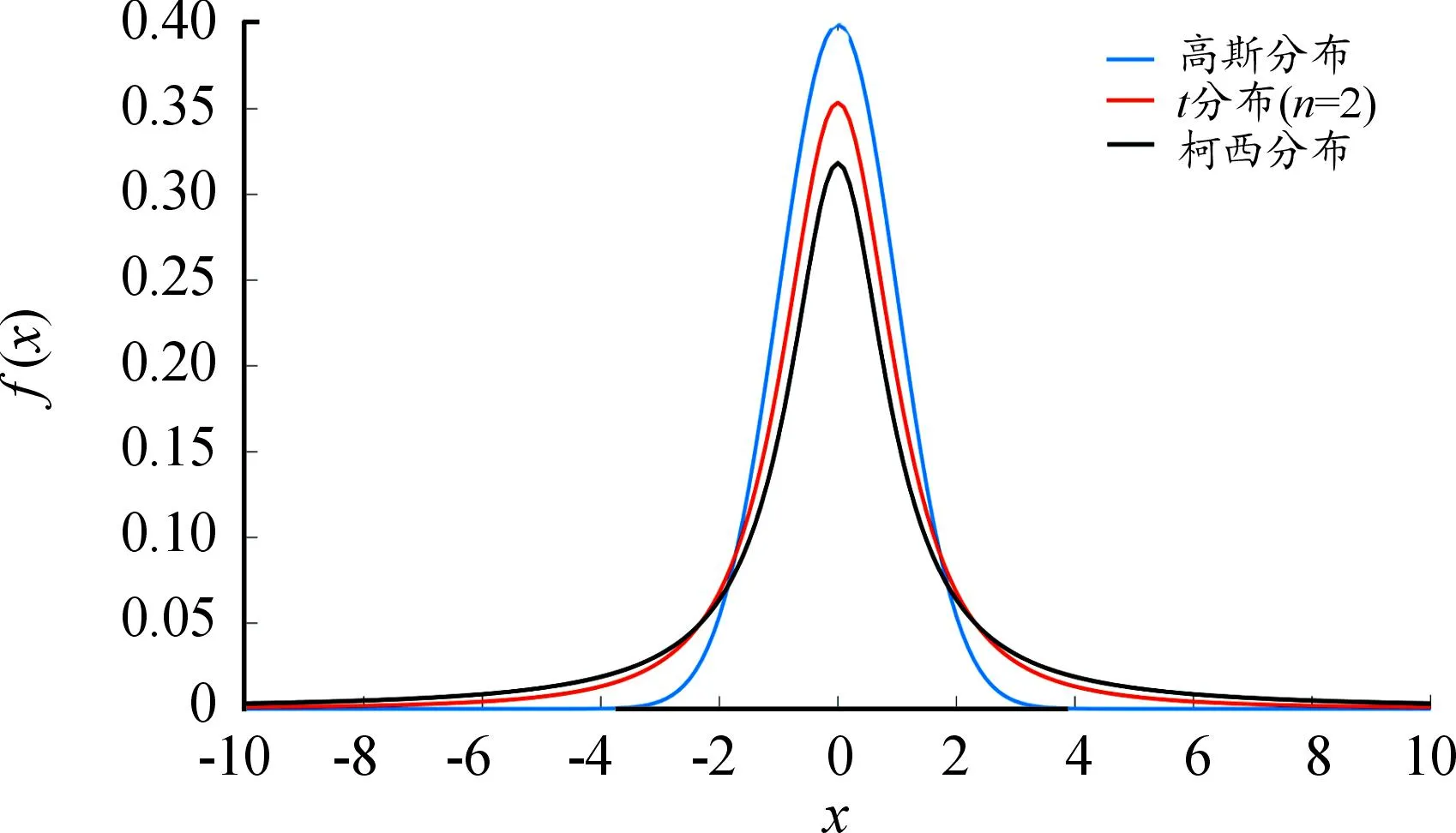
图5 高斯分布、t分布、柯西分布曲线

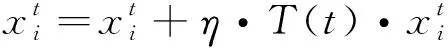
(14)

式中:η为步长参数;T(t)为以算法的迭代次数t为自由度的t变异。

若η为一个常数,并不利于算法的寻优,在PSO算法前中期,η应较大些,有利于跳出局部极值,算法后期,η应较小些,提高收敛能力。因此本文采用一种指数型的变异步长:

η=expt(-d/D)

(15)

式中:d为当前迭代步长;D为最大迭代步长。

为了进一步增强粒子跳出局部最优的能力,提出基于t分布变异的策略。每次迭代完成后,在最优解附近生成基于t变异的新解并对比取优,变异如式(14)所示。前期算法处于探索阶段,此时变异的步长需要大一些,扩大粒子的搜索范围,增强算法的多样性,随着迭代次数的增加,粒子已逐渐接近最优解,算法进入局部搜索阶段,此时需要较小的步长来保证算法在最优解附近进行小范围的精确搜索。

在粒子群算法中,粒子通过自身历史最优与全局粒子最优不断调整自身的飞行方向,自适应t变异使得算法在迭代前期会产生较大的扰动,算法逃离局部极值的能力得到增强,避免局部极值对粒子飞行轨迹的误导,进一步提升算法的收敛速度,收敛后期,随着扰动的减小,算法会在局部位置进行精确搜索,配合蜘蛛移动策略,使得算法有更好的局部寻优能力。

2.5 改进粒子群算法(ICPSO-CT)的执行步骤

具体执行步骤如下。

步骤1：初始化种群,设置最大迭代次数、种群数量、问题维度,按式(7)—式(9)初始化种群的位置。

步骤2：计算各粒子的适应度值,找出个体最优值pb与全局最优值gb。

步骤3：生成概率p,若p<0.3,按式(12)更新粒子速度,否则,按式(13)更新粒子速度。

步骤4：根据式(2)计算粒子的位置,并对粒子做越界处理。

步骤5：执行t变异策略,并对粒子做越界处理。

步骤6：判断是否达到最大迭代次数,若是,则进行步骤7,否则进行步骤2。

步骤7：结束程序,输出算法找到的最优结果。

3 函数测试及结果分析

3.1 测试函数

本文选取了15个基准测试函数,包括9个单峰函数和6个多峰函数。单峰函数因其极值的唯一性,常用来测试算法的收敛速度。多峰函数具有多个局部最优,几乎难以优化,一般用来测试算法的收敛精度。基准测试函数信息如表2所示。

3.2 实验环境

测试环境如下:Windows 10操作系统,处理器为Intel(R) Core(TM) i5-11400H @ 2.70 GHz,在Matlab 2018a上进行测试实验。

3.3 算法参数设置

为验证所提出的改进算法(ICPSO-CT)的有效性,选取原始粒子群算法(PSO)、IPSO-CSC[15]、黑寡妇算法(BWO)[18]进行对比。为避免实验的随机性,设置各个算法的种群数为50,最大迭代次数为100次,在每个测试函数上独立运行30次,记录各自的平均值、标准差及最优值。算法参数设置如表6所示。

表6 算法参数设置

3.4 单峰函数测试

4种算法在单峰函数的测试结果如图6所示,表7给出了实验统计结果。可以看出在9个单峰函数测试中,ICPSO-CT算法的收敛速度最快,且收敛速度明显优于IPSO-CSC,这是因为同Circle映射的种群初始化相比,融合了Circle映射与精英反向学习策略的种群初始化不但提升了种群质量,而且更加丰富了种群多样性,进而加快算法的收敛速度。在函数F1—F8上,ICPSO-CT与IPSO-CSC均找到了最优解,但在函数F6、F8上ICPSO-CT算法的平均值和标准差均低于IPSO-CSC且均为0,而平均值与标准差可以反映算法的寻优精度与稳定性,说明通过引入蜘蛛移动策略,不仅加快了算法的收敛速度,同时还增大了粒子的搜索范围,避免了基本粒子算法存在的搜索盲区,提升了算法的收敛精度。对于函数F9,4种算法均没有找到最优解, IPSO-CSC找到的最优解精度最低且平均值最小,说明在函数F9上,IPSO-CSC拥有较好的普适性。但对于总体单峰函数测试效果而言, ICPSO-CT具有更强的适应性。

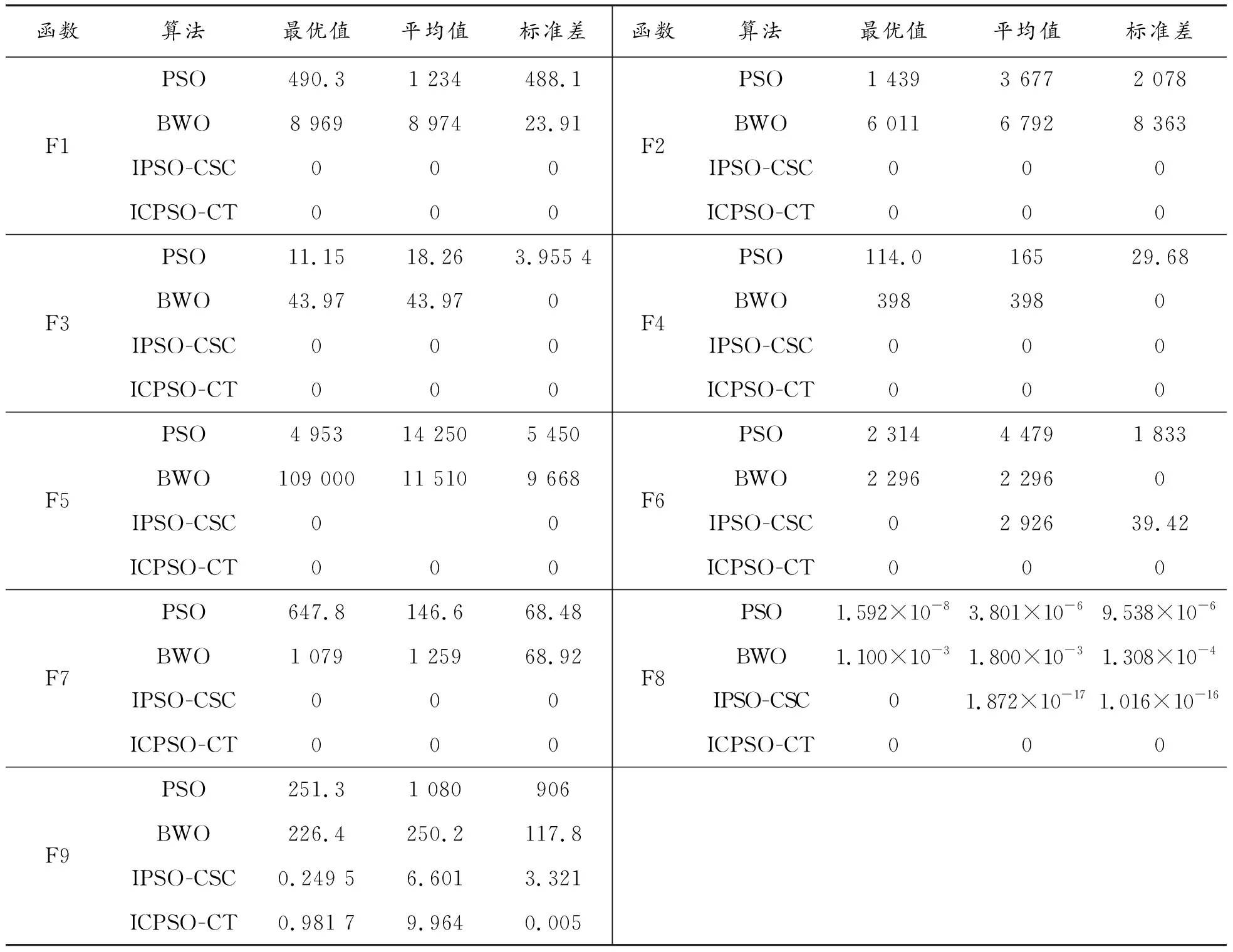
表7 单峰函数测试结果

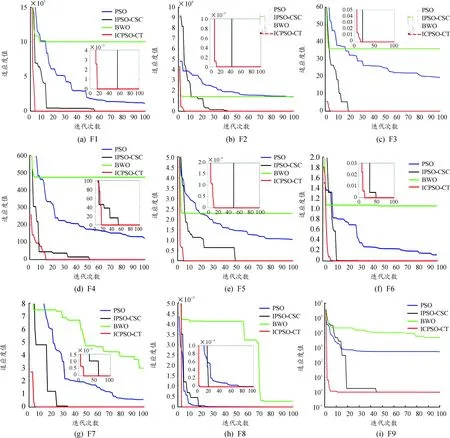
图6 单峰函数测试结果曲线(30D)

3.5 多峰函数测试

图7给出了4种算法在多峰函数的收敛曲线,实验统计结果如表8所示。可以看出ICPSO-CT算法明显快于其他3种算法,进一步说明了融合了Circle映射与精英反向学习策略的有效性。在测试函数F10、F14、F15上,ICPSO-CT可以在较小的步长内找到最优值,证明算法在多峰函数上依然有良好的寻优能力,这是因为通过引入蜘蛛移动策略改变了粒子的飞行方式,扩大了算法的搜索范围,从而加快了算法收敛速度,而由于方向因子的存在,使得粒子在收敛后期围绕着自身历史最优与全局历史最优进行震荡式来回搜索,极大地提升了粒子跳出最优的概率。在函数F14上,虽然ICPSO-CT存在短暂的停滞,但很快跳出并找到理论最优解,说明算法有很强的收敛能力,证明算法拥有很强的跳出局部极值的能力,这是因为自适应t变异策略的存在,粒子的搜索范围会得到进一步提升,当粒子陷入局部最优时,仍然有一定几率摆脱局部极值的束缚,再结合震荡式来回搜索,算法跳出局部最优能力得到极大提升。在函数F10上,只有ICPSO-CT找到了最优解,这无疑再次证明了算法跳出局部最优的能力。在函数F12和F15上,ICPSO-CT与IPSO-CSC均找到了理论最优解,但IPSO-CSC的平均值与理论最优解并不相等,而ICPSO-CT的最优解与平均值相同,说明在多峰函数上算法依旧具有很强的稳定性。

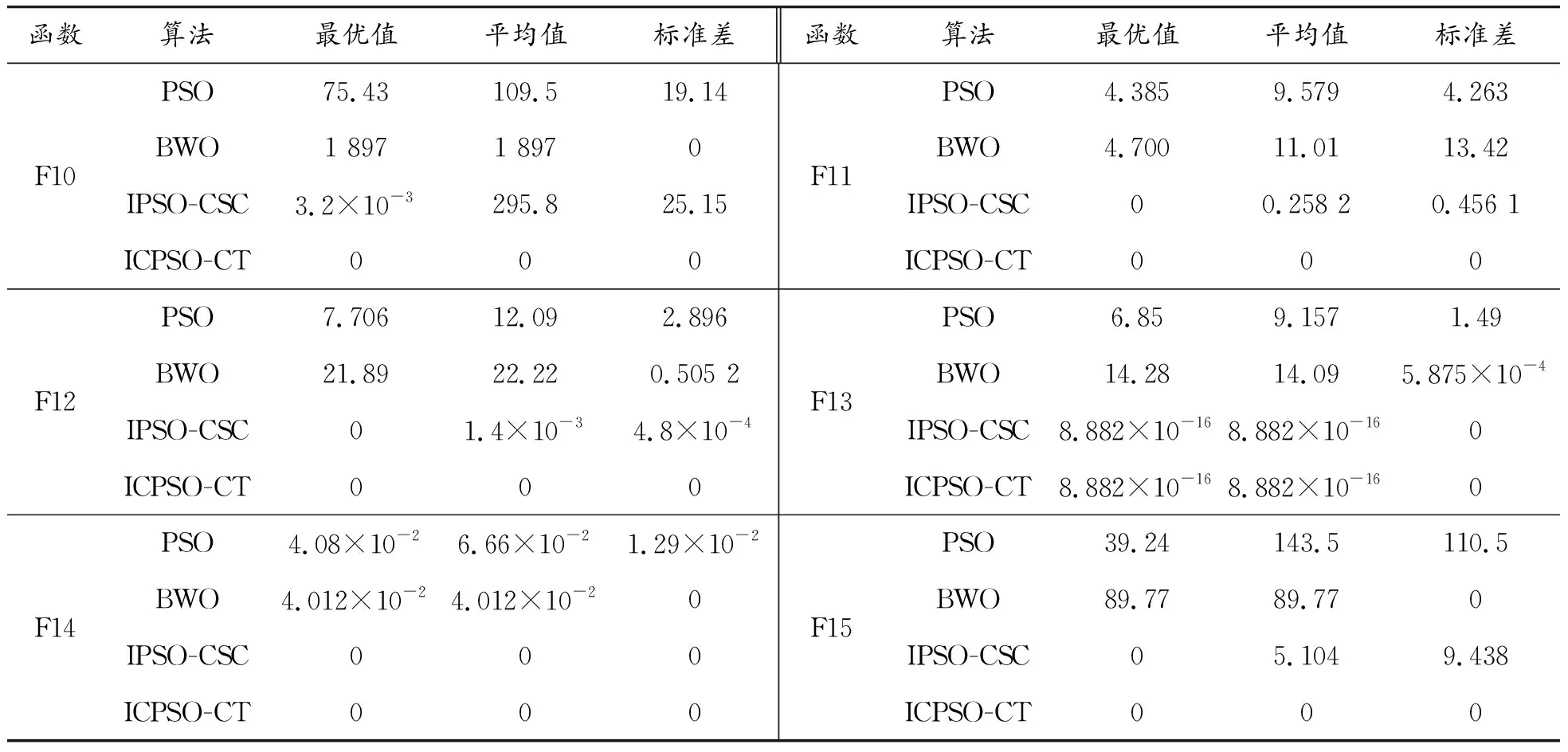
表8 多峰函数测试结果

3.6 高维函数测试

为进一步测试函数的收敛稳定性,将ICPSO-CT与IPSO-CSC在100维的函数F1、F6、F13、F15进行实验。图8给出了收敛曲线,实验统计结果如表9所示。在函数F1、F6、F15上,虽然ICPSO-CT与IPSO-CSC均找到了理论最优解,ICPSO-CT的最优解与平均值、方差均为0,说明在高维函数上ICPSO-CT依旧有稳定的寻优性能。在F13上,2种算法均没有找到最优解,且有相同的收敛精度,但ICPSO-CT算法所用的迭代步数较少,说明融合了Circle映射与精英反向学习策略在高维函数上依旧保持有效性。综合以上图表可以得出:在迭代步长相同时,ICPSO-CT的收敛精度小于其他3种算法,在收敛精度相同时,ICPSO-CT的收敛速度较快。说明ICPSO-CT较其他3种算法而言,在收敛速度、收敛精度和跳出局部最优能力3个方面有较大优势。

表9 高维函数测试结果曲线(100D)

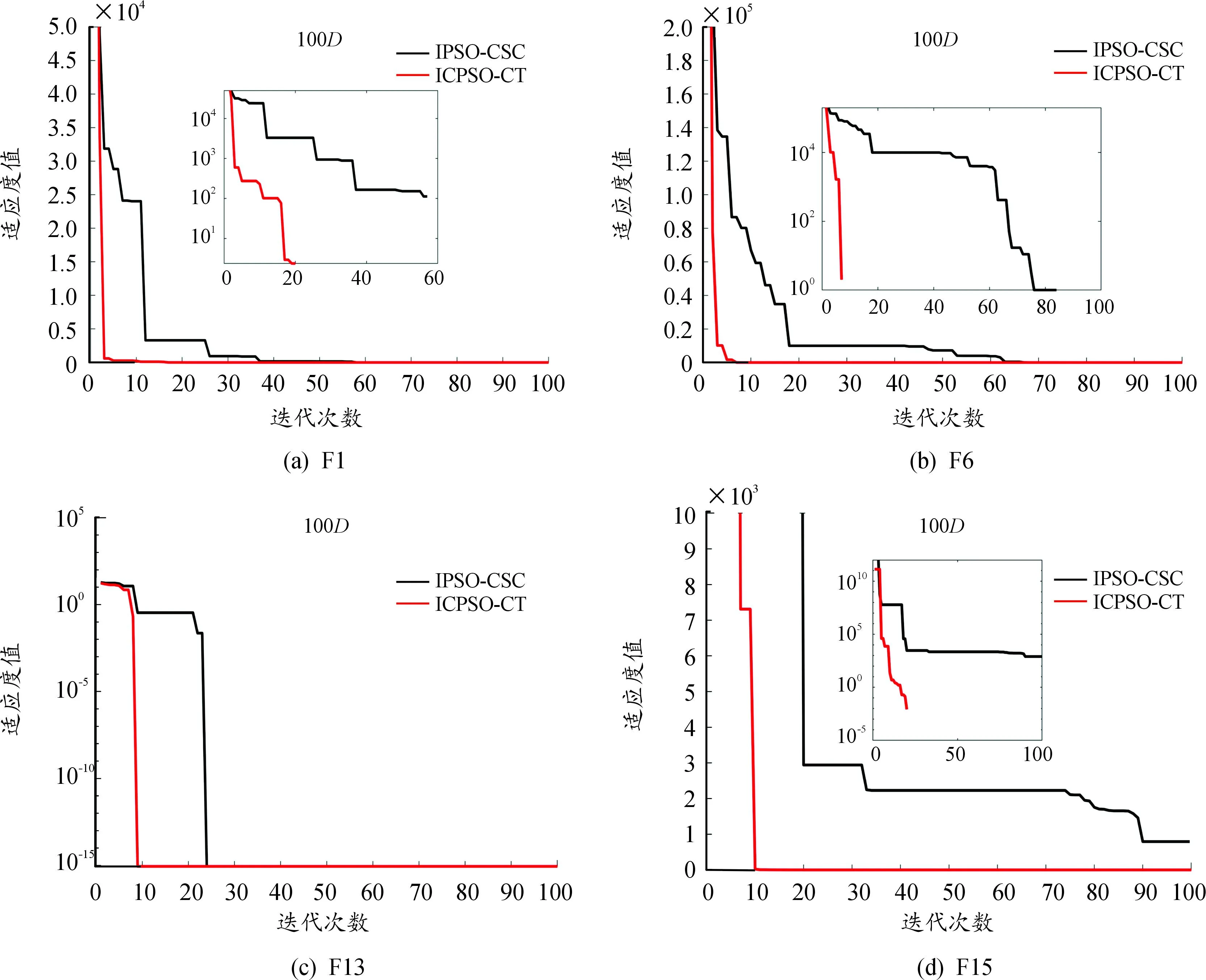
图8 高维函数测试结果(100D)

4 结论

针对基本粒子群算法存在的缺陷,提出一种混合策略改进的粒子群算法。首先,通过融合Circle映射与精英反向学习策略进行种群初始化,提升种群的质量,有利于加快算法的收敛速度;然后通过改变惯性权重w,学习因子c1、c2和粒子速度更新公式,更好地平衡ICPSO-CT全局搜索与局部勘探的能力;最后提出自适应t变异策略,提高了算法的寻优精度与跳出局部最优的能力。通过15个测试函数表明算法在不同维度的单峰函数、多峰函数上具有较好的收敛精度和良好的寻优稳定性。

通过实验可以发现,若将初始种群点全部设在边界处,在单峰函数上算法的收敛速度和寻优精度会得到进一步加强,这可能是与实际生活中大部分最优解均在边界处取得有关。