基于弹塑性模型的某舰炮抽壳力仿真计算
2024-02-03郝攀,张冰,梅帅
郝 攀, 张 冰, 梅 帅
(1.海军驻郑州地区军事代表室, 河南郑州 450015; 2.中国船舶第七一三研究所, 河南郑州 450015)
0 引言
抽壳是舰炮射击过程的重要环节,舰炮射击后,留在炮膛内的空药筒被抽壳机构抽出并被排壳机构排出炮外,否则,滞留的药筒将影响下一发射击,进而影响舰炮连发性能。 为使舰炮射击开闩后药筒在射击振动等因素作用下不会提前出膛,保证连发射击时正常抽壳,一般通过弹炮匹配性设计赋予药筒抽壳时一定的抽壳阻力。
抽壳过程是一个包含弹塑性变形、接触、摩擦等复杂因素的瞬态动力学过程[1],影响抽壳力的因素较多,主要有弹炮间隙、抽筒子与药筒力学性能、药筒与炮膛的摩擦系数、最大膛压等[2]。 曾志银等[3]利用ANSYS 有限元非线性分析功能, 建立了身管与药筒的接触二维非线性有限元模型, 利用直接求出自由度藕合节点约束反力的方法获取抽筒力;汪衡等[4]采用ANSYS/LS-DYNA 显式动力分析软件建立了二维的药筒与身管模型, 对药筒整个发射过程进行数值仿真, 从仿真结果中提取有用的相关数据进行退壳力的计算;康艳祥等[5]采用有限元方法建立了某自动武器抽壳过程仿真模型,模型中忽略了温度的影响,把药筒塑性变形简化为双折线模型, 给出了抽壳力随时间变化曲线;倪璐瑶等[6]通过理论计算、数值分析和试验方法计算抽壳力,分析了最大膛压、初始间隙、药筒壁厚与抽壳力的关系;谭波等[7]建立了抽壳机构的有限元动力学仿真模型,模型中未考虑塑性材料加工硬化行为,得到了抽壳力随时间的变化曲线和药筒速度随时间的变化曲线,分析了抽筒模板位置变化对药筒速度的影响;孙晓雄等[8]建立了药筒及炮膛轴对称二维CCAE 有限元模型,模型中考虑了药筒不同区域不同力学性能, 分析了不同温度及不同药筒材料对抽壳性能的影响;程斌等[9]使用双线性材料模型建立了某小口径火炮抽壳过程有限元模型,计算了抽壳力, 对不同膛压下的抽壳过程进行了研究,分析了发射后药筒再进膛的状况。
以上诸多抽壳过程的研究文献中, 有的利用的二维平面模型,有的利用的是解析模型,有的采用的简易的双折线塑性模型, 研究的侧重点有所不同, 结果也千差万别。本文在前人研究的基础上,建立了抽壳过程弹塑性有限元动力学模型, 采用Johnson-Cook 本构模型描述药筒弹塑性大变形行为,模型中考虑了应变率、温度及材料硬化的影响。详细分析了药筒贴膛及抽壳过程的力学行为,明确了药筒贴膛规律及应力应变分布规律, 定量地给出了抽壳力数值。
1 抽壳动力学仿真模型
1.1 抽壳机构有限元模型网格
根据实际工程尺寸建立抽壳机构三维装配模型,模型主要有身管、药筒、抽筒子及闩体组成,然后对各个构建划分划分网格,如图1 所示,模型中共有636432 个单元。
1.2 边界条件及载荷
对身管进行全约束,约束闩体x、y 移动及xyz 转动自由度,约束抽筒子y 移动自由度,在抽筒子转轴处建立转动自由度。 药筒为自由状态,药筒外表面与身管内表面、药筒地面于闩体表面、 抽筒子抽壳面与药筒底缘内面分别建立硬接触,药筒与身管摩擦系数为0.1,其余摩擦系数为0.15。
在药筒内表面施加火药气体压力, 压力曲线如图2所示。
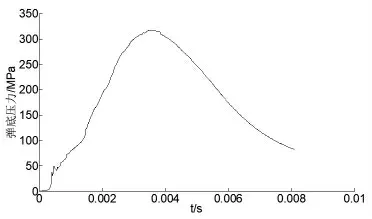
图2 膛底压力曲线
1.3 材料本构模型
身管、闩体及抽筒子采用线弹性本构模型,弹性模量为206000MPa,泊松比为0.35。 药筒在发射时存在较大弹塑性变形,采用Johson-Cook本构模型模拟药筒在高压作用下的力学行为,即:
式中:σ、εp、ε·0分别为等效应力、塑性应变、参考应变率(准静态试验下的材料应变率,常见值为1×10-3);A、B、C、k1 和k2 为材料常数;T0为室温、TM材料熔点温度、T 为膛内温度。
药筒本构模型参数参照文献[9],见表1。

表1 药筒材料本构模型参数
2 计算结果分析
通过弹塑性动力学有限元数值仿真, 获取药筒与炮膛动态应力分布,为分析药筒动态贴膛过程,分别截取药筒贴膛前、与炮膛协同变形及平衡态的应力云图,如图3所示。

图3 药筒贴膛过程
分析图3(a)可知,由于药筒与炮膛之间存在初始间隙,在膛压作用下,药筒开始径向自由膨胀,在没有接触炮膛之前,首先向左运动至与闩体镜面接触。由此可以明确,药筒在运动及变形过程中,首先贴闩,然后开始贴膛。随着膛压继续增大,药筒继续变形,直到与炮膛内壁接触后一起膨胀变形,如图3(b)所示,当膛压达到峰值时,药筒与炮膛变形达到最大,在此过程中,药筒出现一定程度塑性变形。 随着膛压下降,炮膛开始弹性恢复,同时迫使药筒也开始共同收缩,应力状态如图3(c)所示。当膛压完全消失后,炮膛与药筒共同收缩至平衡状态,应力状态如图3(d)所示,由于共同收缩过程中炮膛对药筒存在反向加载,因此,达到平衡状态时药筒与炮箱处于贴紧状态,存在一定过盈量,抽壳过程需要克服抽壳阻力。
为分析平衡状态时药筒与炮膛的受力状态, 沿药筒口部至底部方向依次提取多个炮膛内表面节点应力,提取点位置如图4 所示。 根据提取应力值, 绘制成应力曲线,如图5 所示。

图4 节点应力提取位置示意图
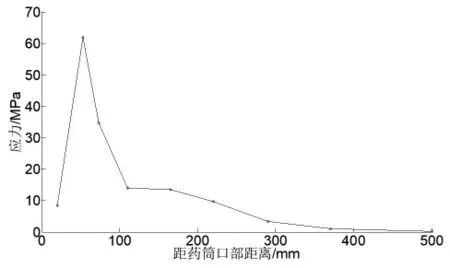
图5 炮膛与药筒接触应力
分析图5 可知, 炮膛与药筒口部圆柱段及斜肩接触部应力较大,向药筒底部方向依次降低。这是因为发射时主要靠药筒口部圆柱段闭气, 根据药筒分区域热处理要求,药筒口部材料屈服强度较低,更容易塑性变形,收缩至平衡状态时炮膛与药筒之间过盈量较大。
图6 为抽壳阻力曲线,由图可知,药筒与炮膛收缩至平衡状态后抽壳阻力不再变化, 保持在13320N 左右,药筒被抽出时与炮膛分离,抽壳阻力将为0。
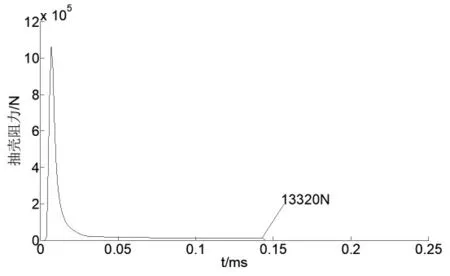
图6 药筒速度曲线
根据抽壳机构工作原理,抽壳时抽筒子作用于药筒,克服抽壳阻力后使药筒瞬时获得一个较大的初速, 沿排壳通道排出炮外。 图7 为药筒速度曲线,由图可知,最大抽壳速度为18.9m/s,能够满足连发射击对抽壳的要求。

图7 药筒速度曲线
3 结论
本文采用Johnson-Cook 本构模型开展了弹塑性抽壳过程动力学仿真, 分析了药筒动态贴膛规律及其贴膛过程中药筒与炮膛动态应力分布,得出主要结论如下:
(1)药筒在运动及变形过程中,首先贴闩,然后开始贴膛。当膛压完全消失后,炮膛与药筒共同收缩至平衡状态,达到平衡状态时药筒与炮箱处于贴紧状态,存在一定过盈量,即存在抽壳阻力。
(2) 药筒与炮膛收缩至平衡状态后抽壳阻力保持在13320N 左右,不再变化;抽壳后药筒瞬时获得较大的初速,最高可达到18.9m/s,此初速能够满足连发射击工况下的设计需求。
