大时滞过程控制方法比较研究

陈宇昊， 王玎楠， 朱建国， 郑天歆

（1.中国空空导弹研究院， 河南洛阳 471009； 2.中国人民解放军95607 部队， 四川成都 610011；3.空装外场局， 北京 100038； 4.中国人民解放军94314 部队， 河南郑州 450000）

0 引言

时滞现象是一种时间上的延迟， 是指系统的扰动不能被及时反映到控制作用上，控制作用往往滞后一定时间才能反映到对象输出上， 调节效果不能被适时反映的现象。 一般认为纯滞后时间与系统的时间常数之比θ〉0.5，则认为该过程为大时滞过程。

1 内模控制方法研究

1.1 内模控制的研究状况

内模控制（IMC）主要特点是结构简单、设计直观简便，具有较少的在线调节参数和易于调整的特点。典型的设计方法包括零极点对消、预测控制、自适应IMC、采用模糊决策和仿人控制等。此外，IMC 还具有良好的鲁棒性能、跟踪性能和动态性能等控制性能[1]。

1.2 内模控制原理

内模控制等效结构图如图1 所示。

图1 内模控制等效结构

根据图1 可得式：

1.3 内模控制器的设计

第一步：分解对象模型

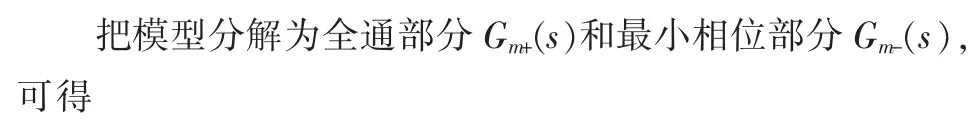
Gm+（s）包含Gm（s）中的纯滞后环节和右半S 平面的零点，且｜Gm+（s）｜＝1，∀ω

通常，Gm+（s）形式如下：

第二步：模型误差的鲁棒性设计

为了能够抑制模型误差对系统的影响、 增强系统的鲁棒性，在内模控制器中加入低通滤波器F（s），一般情况下F（s）只需要取如下形式：

取n 为1。 λ 为时间常数，一般情况下取（0.1-2）λ，选取（0.1，0.5，1.2）τ，使得λ=5，25，50，100。 按照λ 的四种可能分别进行仿真，得如图2 所示。 比较得知λ 取5 时仿真效果最好，可得出内模控制器为：

图2 分别取5，25，50，100 时的仿真图

1.4 内模控制器的仿真研究

系统给定点输入r（t）=1（t），扰动输入d（t）=0.1×1（t-700），根据扰动D（s）加在Gp（s）之后的仿真图与加在其之前的仿真结果对比如图3 所示。

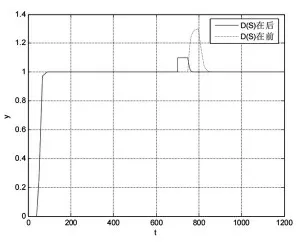
图3 扰动加在对象之后

分析仿真图可得，扰动加在之前时，它的反应时间相较于加在之后延迟了50s，加在之前的系统对扰动的反应明显更强烈，超调更大，但最终都能较快的归于稳定。

2 史密斯预估控制方法研究

2.1 史密斯预估控制的研究状况

Smith 预估控制的主要目的是对纯滞后进行补偿，通过一个预估模型来估计对象的动态特性， 并将无时滞的被控量反馈给控制器，从而提高系统的控制效果[2]。

2.2 Smith 预估补偿控制原理

Smith 预估补偿控制是一种有效的克服纯滞后的控制方法。 基本原理是在控制器上并联一个补偿环节，用于补偿受控对象中的纯滞后部分。

史密斯预估控制的原理框图如上所示，图中Gc'（s）为控制器的传递函数，Gp（s）=Gp0（s）e-ts为时滞对象的传递函数，Gm（s）=Gm0（s）e-rs是系统的预估模型。

由图4 可以导出闭环系统的传递函数为：

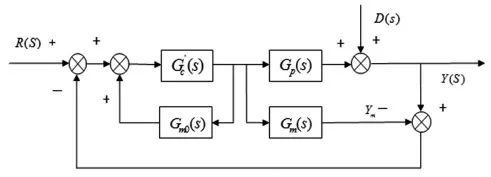
图4 史密斯预估控制系统

图5 改进的Smith 预估控制系统

图6 Smith 预估控制

经过Smith 预估控制后，系统的特征方程已经不包含纯滞后项， 从而使系统的控制性能大大改善。 实际上，Smith 预估器的模型参数与被控时滞对象肯定存在误差，因此系统的特征方程仍然带有时滞因素。

2.3 改进后的Smith 预估器

本文提供一种表现出色的改进方案。该改进方案旨在提高常规Smith 预估控制系统的性能，同时保持简单易实施的优势。 通过减小稳定域极限的压力，该改进方案成功克服了常规Smith 预估控制系统的局限性。 其结构如下：

最显著优化方案就是用Gn0（0）代替了原来的Gm0（0）。该系统对参考输入的稳态误差为零， 同时对扰动具有抑制作用。

2.4 Smith 预估控制器的仿真

由之前的设计选择， 组成Smith 控制的Simulink 仿真图，再根据需要在仿真的同时调试参数，并且在时间t=200s 时加入一个幅值为1 的阶跃扰动，可得结果如下：

由上图的仿真结果可观察得到，Smith 预估控制方式的目标值跟踪特性较好，其抗扰性能较好，消灭静态误差的能力也很强。

3 PID 控制方法研究

3.1 PID 控制方法的研究状况

工业控制过程中，目前最广泛应用的控制方法是PID控制，因其结构简单、稳定性好、通用性强、鲁棒性好、可靠性高及使用方便等优点，成为最通用的控制方法。 PID控制的一个重要问题是参数整定， 即确定控制器的比例度、积分时间和微分时间[3]。

3.2 PID 控制原理及算法

图7 是典型PID 控制系统结构图， 在PID 调节器作用下对误差信号分别进行比例、积分、微分组合控制，调节器的输出作为被控对象的输入控制量。 PID 控制器是一种线性控制器，它根据给定值r（t）与实际输出值y（t）构成控制偏差。

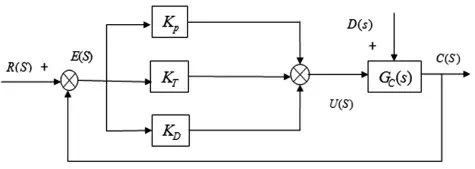
图7 典型PID 控制系统结构图

PID 的控制规律为：

为有效提升房建监理质量，应当提升从业人员的职业水平、专业素养，保证监理人员始终具有高度的责任心、对整个工程的质量进行监管，对居住者的生命财产健康负责。因此，在进行房屋建设监理时，需要事先对监理计划进行制定、预先选择有效的监理措施，对相关不安全因素进行预防，降低质量问题发生几率。除此之外，监理从业人员，需要具备过硬的专业素养，可认真细致的检查工程实际情况，工作严谨、态度认真，脚踏实地、注意细节。严格按照相关规定进行细节检查，透过现象看本质，提升质量监理的有效性。

相应的传递函数为：

式中：KP—比例系数；TI—积分时间常数；TD—微分时间常数。

而通常干扰通道中还会有纯滞后环节， 使被调参数的响应时间滞后一个值τ，即Yτ（t）=Y（t-τ），表明调节过程沿时间轴平移了一个τ 的距离， 所以干扰通道出现有纯滞后不会影响系统调节质量， 但干扰进入系统中的不同位置也会产生不同的作用。

PID 控制器各个校正环节的作用如下：

比例环节：系统的响应速度和调节精度同KP呈正相关， 但KP过大则会产生超调，KP过小则会使响应速度变慢，使系统静动态特性变坏。

微分环节： 微分作用系数Kd可以改善系统的动态性能，但Kd过大会使系统的调节时间延长，抗干扰性能降低。

积分环节：积分时间常数Ti越大积分作用越弱，反之则越强。积分作用系数Ki可以消除系统的稳态误差，但Ki过大会在响应过程产生较大超调，产生积分饱和现象，过小则会使系统稳态误差不易消除。

3.3 PID 控制参数整定方法

一般情况下，PID 控制器的参数整定方法包括比例系数KP、积分时间Ti和微分时间Td这三个参数的选取。 调节器参数的整定方法通常可以分为两大类： 一种是理论计算整定法；另一种方法是工程整定法。 在工程中应用较多的是工程整定法，如临界比例度法、衰减曲线法、经验试凑法和反应曲线法。

3.4 PID 参数整定

本文是在Matlab 环境下进行设计与仿真。 依据主动悬架系统性能指标要求和一些基本的整定参数的经验，选择不同的PID 参数进行仿真。 辅以Z-N 整定，这样既直观方便、计算量小，又便于调整与改进。

（1）只加入比例作用，求出系统等幅振荡时的Ku、Tu

用二分法试凑出比例调节器能产生等幅振荡时的Ku为0.37，由图8（b）得出的Tu有三组数据，分别为118.5、117.1、115.6，三个数据平均值可得Tu≈117.1。

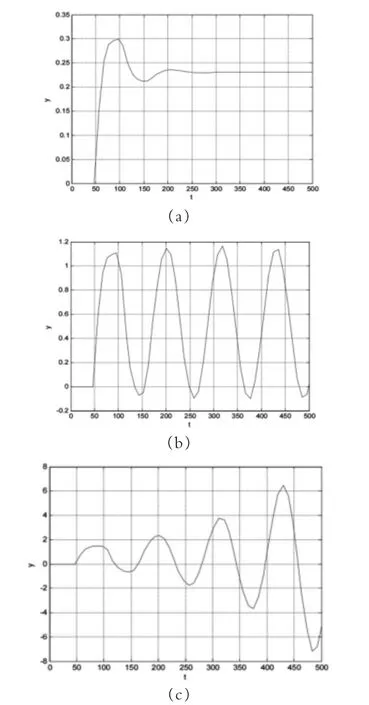
图8 不同Ku 时的仿真图

此时处在收敛状态，应该适当增大Ku。图8（a）图中仿真稳定值为0.22 左右，远远小于预定值1，图8（c）中Ku增至0.5 后发现曲线呈发散状态， 由二分法最终确定Ku取0.37 时系统等幅振荡效果最佳。

（2）已知Ku=0.37，Tu=117.1，当比例、积分、微分都起作用即PID 控制时：

Kp=0.6Ku=0.222，

则有：观察图9 可知，虽然PID 控制器的各项参数都是通过理论计算得到的，但仿真结果并不理想。而图10中是按理想状态下的参数来的，依然在振荡。尝试着继续减小Kp的值，消除静差的速度变快，但是以牺牲响应速度为代价的。

图9 PID 控制

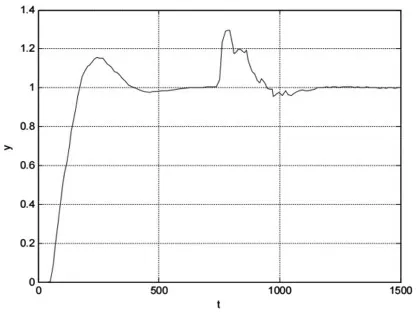
图10 调整后的PID 控制

适当继续减小Kp的值，可得到图10 中Kp为0.01 时的仿真结果，系统的稳定性变好但抗扰性能一般。即Kp减小时，系统跟踪性能变差。

4 控制方法的比较研究

在参数匹配时，内模控制的上升时间很短，动态响应速度较快、无超调、稳定性较好；PID 控制方式的上升时间要长，动态响应速度较慢，有一定的超调，稳定性稍差；PID 控制方式各方面的性能均差于内模控制方式[4]。

在参数失配时，在加入扰动后PID 控制系统的响应较大，波形出现较大波动，抗扰性较差。T 的增大对内模控制系统和PID 控制系统都起到优化的作用。 对于经调整后的PID 控制方式，τ 的增加对系统影响较小。 对于内模控制方式， τ 的增加对系统产生的影响表现在鲁棒性较差。其次，对于K，Τ，τ 减小后的仿真结果显示，K 的减小使PID 控制方式的系统鲁棒性和抗扰性都变好，但内模控制方式的动态响应速度变差。T 的减小对内模和PID 控制方式的影响都较小。 T 的减小并没有因为减小时滞而改善系统的控制品质，而是出现了负振荡。

5 结论

对于一个大时滞系统来说，PID 控制方式的系统除了抗扰性差之外，动态响应特性和鲁棒性相对较好。 PID 控制方式对参数不敏感，只要K，Τ，τ 发生变化，系统就会相应地发生变化。 根据上面的研究，K，Τ 的增加而τ 不变较有利于提高系统的控制品质。