基于薄片漏斗试样的N06230合金高温低周疲劳性能研究
2024-02-01于明明韩光照谢逍原蔡力勋
于明明,韩光照,谢逍原,蔡力勋
(1.东方电气集团东方锅炉股份有限公司,自贡 643001;2.西南交通大学力学与航天航空学院,成都 610031)
0 引 言
N06230合金是一种综合性能优良的Ni-Cr-W-Mo系高温合金,具有出色的抗氧化、抗氮化性能和优异的高温强度及长期热稳定性等,被广泛用于航空航天、电力、化工过程等行业[1-2]。随着太阳能光热发电行业的发展,该合金已成为塔式熔盐光热发电机组吸热器主要组件吸热管的首选材料。吸热器在运行过程中会受到设备启停时的升降温的影响,而温度波动所产生的交变应力会对吸热管造成疲劳损伤。因此,研究N06230合金管的高温低周疲劳性能对分析吸热器的耐久性有重要意义。
根据GB/T 26077—2021,用于低周疲劳试验的板状试样厚度应在2.5~5.0 mm范围;对于厚度小于2.5 mm的板状试样,需设计约束几何结构以及与试样几何结构相匹配的抗屈曲装置以防止循环失稳,且抗屈曲装置与试样之间的摩擦力会对试验结果造成影响。由于N06230合金吸热管上截取的工作段等直薄片试样厚度不满足直接开展低周疲劳试验的要求且不便施加抗屈曲装置来防止循环失稳,因此难以采用上述试验方法得到对称循环疲劳下完整、精确的材料Manson-Coffin(M-C)律。为解决此类薄片试样在疲劳试验过程中的循环失稳问题[3-4],MANTIN等[4]设计了一种漏斗圆弧半径和漏斗根部宽度相等的薄片漏斗试样来进行轴向等幅低周疲劳试验,结果表明:当施加的轴向名义应变幅不超过1.5%时,试样均未发生循环失稳;薄片漏斗试样解决了薄片试样疲劳循环失稳问题,但由于缺乏非标准试样弹塑性变形解析表征,该试验采用漏斗根部平均应变幅和截面平均应力幅作为循环应变幅和应力幅以确定材料的M-C律,这与漏斗根部处于单向应力状态的材料代表性体积单元的真实应力幅、应变幅存在较大偏差,因此试验结果难以与标准圆棒试样低周疲劳试验获得的M-C律等效。蔡力勋课题组[5-8]基于能量密度等效理论建立了描述薄片漏斗试样几何尺寸、材料循环应力幅-应变幅关系参数、试验载荷幅和位移幅之间关系的理论模型,并提出了基于薄片漏斗试样获取材料循环应力幅-应变幅关系和M-C律的低周疲劳试验方法;采用多种工程金属材料完成了薄片漏斗试样和标准圆棒试样低周疲劳试验,发现用薄片漏斗试样获得的材料低周疲劳寿命预测曲线与用标准圆棒试样获得的曲线具有良好的一致性。因此,作者采用基于能量密度等效理论的薄片漏斗试样低周疲劳试验方法,设计了国产和进口N06230合金管薄片漏斗试样以及配套弧形夹具,通过高温低周疲劳试验获取材料的应变幅-寿命曲线、循环应力幅-应变幅曲线及M-C律,以期为光热发电机组主组件吸热管的材料选择提供试验参考。
1 试样制备与试验方法
试验材料为国产和进口N06230合金管,规格分别为φ45 mm×1.2 mm,φ50.8 mm×1.5 mm,化学成分见表1。设计的薄片漏斗试样和配套弧形薄片夹具如图1所示。国产和进口合金管薄片漏斗试样的工作段几何尺寸一致,长度H为18 mm,宽度W为10 mm,厚度B为1 mm,漏斗根部宽度T为5 mm,半径R为5 mm,试样两端夹持段宽度L为15 mm。由于2种合金管的规格不同,因此需根据管径设计不同的配套夹具,以保证薄片试样夹持段与夹具密切贴合,即夹具弧形夹持面直径和管直径相同。此外,试样的轴心与夹具轴心应保持一致。
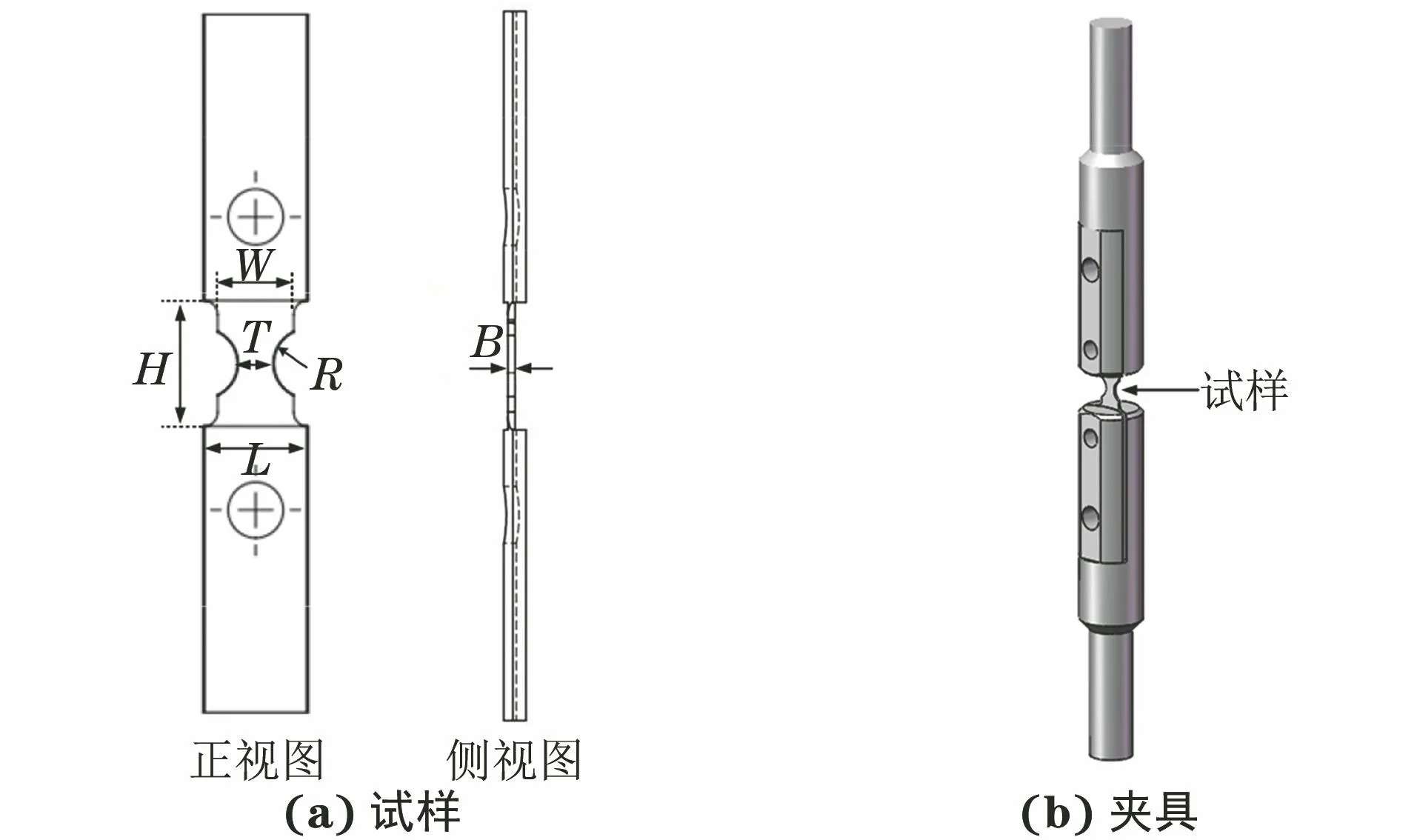
图1 薄片漏斗试样和夹具结构示意Fig.1 Structure diagram of sheet-funnel specimen (a) and fixture (b)

表1 国产和进口N06230合金管的化学成分Table 1 Chemical composition of domestic and imported N06230 alloy tubes
在MTS 809-25 kN型电液伺服材料试验机上进行高温低周疲劳试验,采用配套夹具对薄片试样进行夹持,且夹具与试验机液压夹具之间采用刚性连接,连接系统具有良好的同轴度。将MTS 632.53 F-14型高温应变引伸计(标距为12 mm,量程为-10%~20%)的上下臂分别安装于跨漏斗两侧,用于轴向名义应变控制。试验时的加载应变速率为0.005 s-1,试验机载荷传感器和引伸计精度均为0.5级,试验温度为650 ℃,加热设备为对开式高温大气电阻炉,炉腔内等温区温度控制精度为±1 ℃。选择5~7级应变水平完成等幅循环低周疲劳试验,当试样加载载荷较循环稳定载荷下降20%时,判定试样失效。
2 模型的建立及参数的确定
2.1 模型的建立
循环应力幅-应变幅关系反映的是材料在不同应变幅作用下循环稳定时循环应力幅的响应。在应变循环作用下,循环稳定应力幅-应变幅关系[5-8]可表示为

(1)
式中:σa,εa分别为应力幅和应变幅;εe-a,εp-a分别为纯弹性应变幅和纯塑性应变幅;E为弹性模量;K,n分别为循环应变强化系数和循环应力强化指数。
基于能量密度中值等效和能量密度降维等效,以及有效变形域体积和能量密度等效单元的等效应变与试样加载线位移幅(或侧向加载位移幅)之间的幂律假设[5-8],建立关联材料循环应力幅-应变幅关系参数、试样几何尺寸、试验载荷幅和位移幅之间关系的载荷幅-位移幅模型,基于模型,若已知材料的循环应力幅-应变幅关系参数和试样几何尺寸,可实现材料循环载荷幅-位移幅的精确预测。载荷幅-位移幅模型如下:
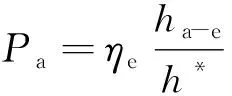
(2)
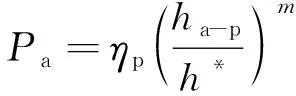
(3)
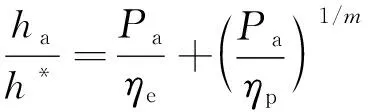
(4)
ηe=k0EA*
(5)
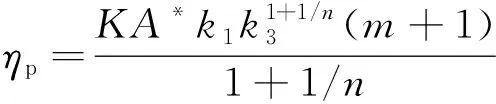
(6)
m=k4/n+k4+k2-1
(7)
A*=(2L-πR)B
(8)
式中:Pa为载荷幅;ha-e,ha-p,ha分别为侧跨漏斗弹性位移幅、塑性位移幅和总位移幅;A*,h*分别为特征面积和特征位移,其中h*=R;ηe,ηp分别为纯弹性和纯塑性加载系数;m为纯塑性加载指数;k0,k1,k2,k3,k4均为模型常数,可通过有限元分析确定。
对载荷幅-位移幅模型整理可得材料循环应力幅-应变幅关系参数模型,即

(9)

(10)
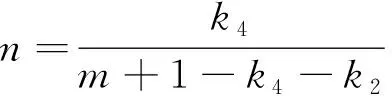
(11)
由高温低周疲劳试验获得循环稳定Pa-ha曲线,其初始线性部分视为纯弹性变形,分别以线性关系和幂律关系回归Pa-ha/h*试验曲线和Pa-ha-p/h*(ha-p=ha-Pa/he)曲线,即可获得he,hp,m,根据式(9)~式(11),可确定E,K,n。
薄片漏斗试样根部通常为疲劳裂纹萌生区,且漏斗根部处于单轴应力状态,因此假设当薄片漏斗试样根部应变幅与标准等直圆棒型疲劳试样应变幅相同时,二者的疲劳寿命相当[5-6]。在薄片漏斗试样疲劳试验中,通过控制引伸计测得的是跨漏斗侧向名义应变幅εa-m,无法直接测得漏斗根部实际应变幅εa-r和应力幅σa-r。因此,需建立漏斗根部代表性单元的应变幅εa-r与εa-m之间及漏斗根部代表性单元的应力幅σa-r与平均应力幅σa-m(载荷幅与漏斗根部横截面积的比值)之间的关系,进而获得漏斗根部代表性单元应变幅εa-r与疲劳寿命Nf的关系曲线。
金属材料的低周循环疲劳寿命可采用M-C律[9-10]描述:
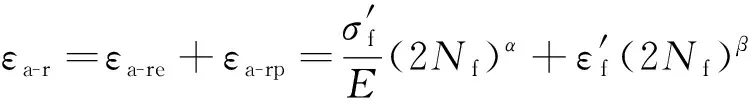
(12)

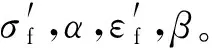
2.2 模型常数的确定
采用有限元分析软件ANSYS对薄片漏斗试样准静态拉伸过程中的弹塑性变形行为进行有限元分析。由于弧形薄片漏斗试样两端夹持段与夹具通过螺栓紧密连接,而中部变形区域为等直段,因此在有限元分析中仅对中部变形区域进行建模分析,有限元网格模型如图2所示。试样主体部分采用SOLID 185单元,最小网格单元尺寸约为0.167 mm,节点总数为19 747个,单元总数为16 200个。模型上端施加固定约束,下端进行位移加载。薄片漏斗试样高温低周疲劳试验时采用的引伸计标距为12 mm,因此取跨漏斗两侧间距为12 mm的厚度方向中部两节点位移差作为跨漏斗位移幅,即为引伸计采集的名义应变转化的位移。
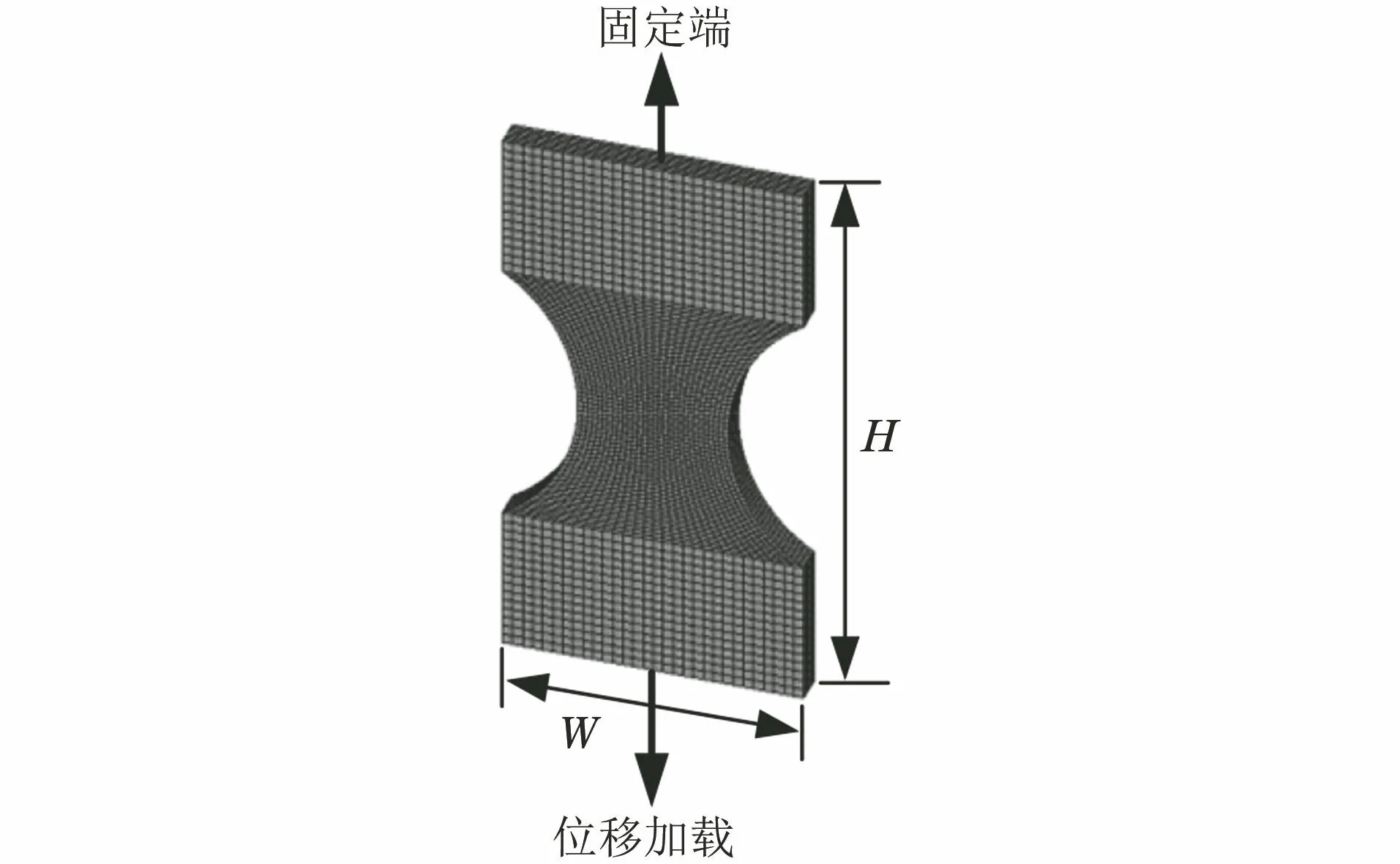
图2 薄片漏斗试样工作段的有限元网格模型Fig.2 Finite element mesh model of working section for sheet-funnel specimen
分别对薄片漏斗试样准静态拉伸过程进行纯弹性分析和纯塑性分析,以确定模型常数。N06230合金管的弹性模量约200 GPa,因此在进行纯弹性分析时,选取E为200 GPa进行数值模拟,获得薄片漏斗试样的纯弹性载荷幅-位移幅曲线。对载荷幅-位移幅曲线进行线性回归,即可获得纯弹性加载系数ηe[11-12]。根据式(3),可确定模型常数k0。
由于载荷幅-位移幅模型是具有材料普适性的理论方程,因此模型常数k1,k2,k3和k4可通过对理想材料(具有相同的K和不同n)薄片漏斗试样进行纯塑性分析确定[11-13]。取K为1 000 MPa,n分别为4, 6, 8, 10, 12,根据式(1)通过给定应力幅计算对应的应变幅,进而通过多线性本构模型输入到有限元分析软件中进行模拟,获得对应不同n的薄片漏斗试样的纯塑性载荷幅-位移幅曲线;采用幂律关系分别回归5条纯塑性载荷幅-位移幅曲线,获得纯塑性加载系数和纯塑性加载指数数据组。根据式(3),定义λ=hp(1+1/n)/[KA*(m+1)],则

(13)
m=k4(1+1/n)+k2-1
(14)
分别采用指数关系和线性关系对λ-(1+1/n)和m-(1+1/n)进行回归,从而确定k1,k3和k2,k4,如图3所示。综上,模型常数k0,k1,k2,k3,k4分别为0.169 2, 0.542 8, 0.985 6, 2.396 0, -0.003 6。
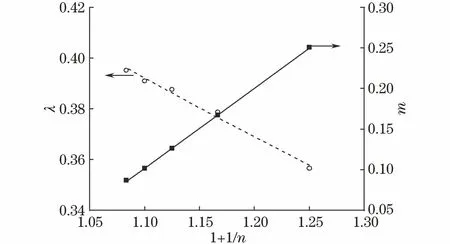
图3 λ与(1+1/n)以及m与(1+1/n)的拟合曲线Fig.3 Fitting curves of λ and (1+1/n) and m and (1+1/n)
2.3 模型的验证
选用不同预设K和n组合的弹塑性材料进行薄片漏斗试样弹塑性数值模拟,获得对应的载荷幅-位移幅曲线,根据薄片漏斗试样高温低周疲劳试验方法和确定的模型常数,预测对应的K和n,绘制循环应力幅-应变幅曲线,并与有限元分析预设的循环应力幅-应变幅曲线进行对比,以此来判断该模型的普适性。将预设的K和n组合通过各向同性多线性本构模型输入到有限元本构关系中。E取200 GPa,K分别取200,500,1 500 MPa,n分别取4,6,8,10,12,所选用的材料常数覆盖了大部分常规工程材料。根据有限元分析获得的载荷幅-位移幅曲线,采用材料循环应力幅-应变幅关系参数模型预测获得E,K和n,进而获得循环应力幅-应变幅曲线,结果如图4所示,并与有限元分析预设的循环应力幅-应变幅曲线进行对比。由图4可知,预测得到的曲线与有限元分析预设的曲线非常吻合。根据GB/T 37782—2019,采用优度评价预测曲线与预设曲线之间的接近程度,拟合优度越趋于1,表明两者之间一致性越高。计算表明所有工况模型预测曲线的拟合优度均高于0.98,说明该模型对于预测材料的循环应力幅-应变幅关系具有普适性和精确性。
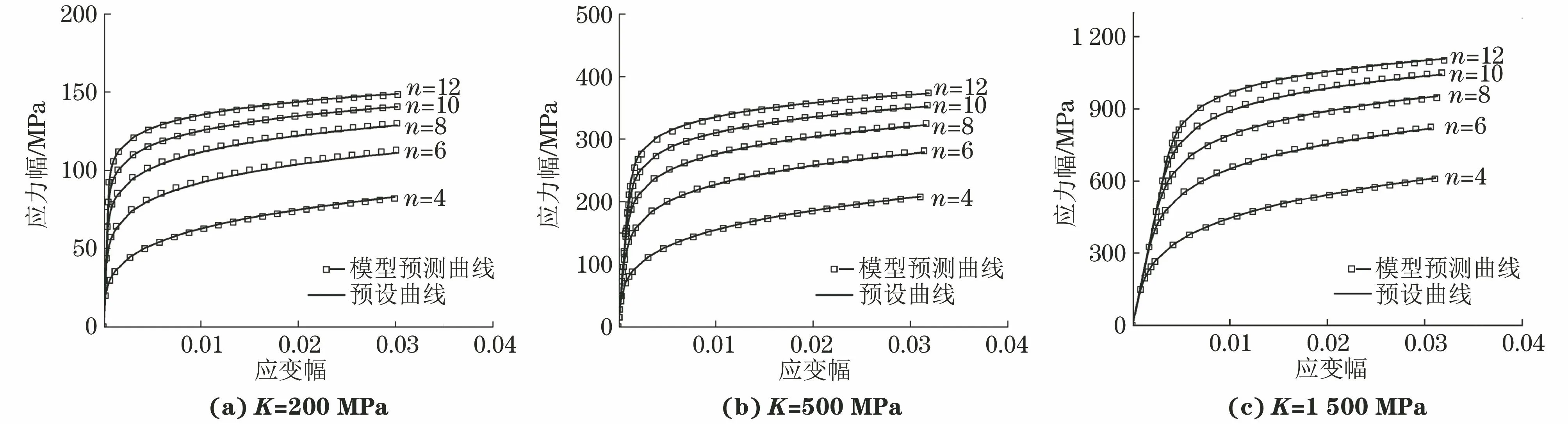
图4 模型预测不同K值下应力幅-应变幅曲线与预设曲线的对比Fig.4 Comparison of predicted stress amplitude-strain amplitude curves under different K values by model with preset curves
3 结果与讨论
3.1 循环应力幅-应变幅关系曲线
对国产和进口N06230合金管薄片漏斗试样进行变幅对称循环加载,获得的在各级名义应变幅控制下的循环稳定载荷-位移滞回环曲线以及Pa-ha曲线如图5所示。分别以线性关系和幂律关系回归Pa-ha/h*试验曲线和Pa-ha-p/h*曲线获得he以及hp和m,代入式(3),计算得到循环应力幅-应变幅关系参数(见表2),进而绘制循环应力幅-应变幅曲线。由图6可知,国产N06230合金管的循环应力幅-应变幅曲线与进口合金管相近。

图5 国产和进口N06230合金管薄片漏斗试样的循环稳定载荷-位移滞回环曲线和Pa-ha曲线Fig.5 Cyclic stable load-displacement hysteresis loop curves and Pa-ha curves of sheet-funnel specimens of domestic (a) and imported (b) N06230 alloy tubes
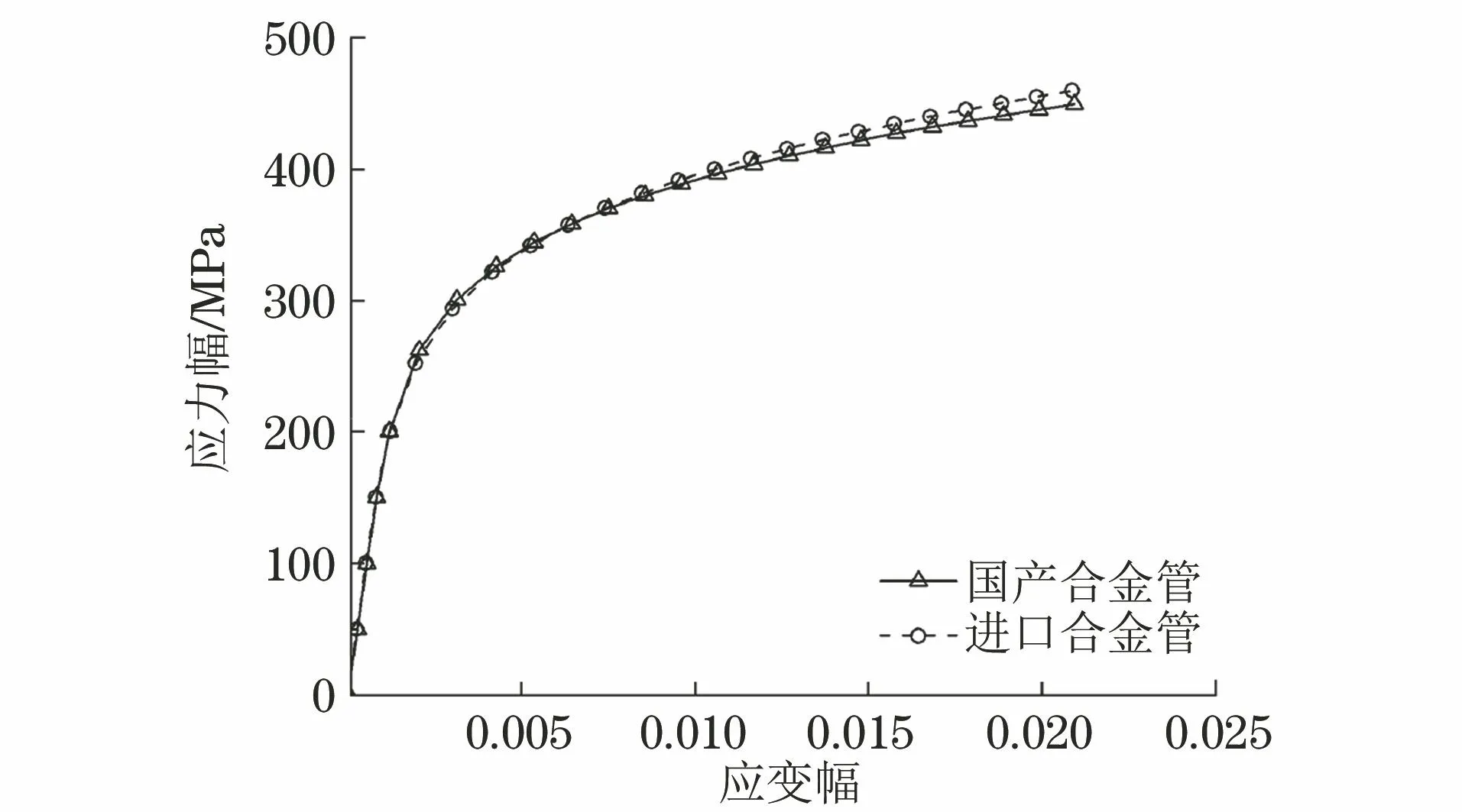
图6 国产和进口N06230合金管的循环应力幅-应变幅曲线Fig.6 Cyclic stress amplitude-strain amplitude curves of domestic and imported N06230 alloy tubes

表2 国产和进口N06230合金管的循环应力幅-应变幅关系参数Table 2 Cyclic stress amplitude-strain amplitude relation parameters of domestic and imported N06230 alloy tubes
3.2 局部应力幅、应变幅的获取
将2种合金管的循环应力幅-应变幅关系代入有限元软件中进行数值模拟,提取名义应变幅εa-m(跨漏斗各6 mm位置节点的位移与引伸计标距的比值)、平均应力幅σa-m、漏斗根部代表性单元的应变幅εa-r和应力幅σa-r,得到εa-r与εa-m之间以及σa-r与σa-m之间关系,如图7所示。
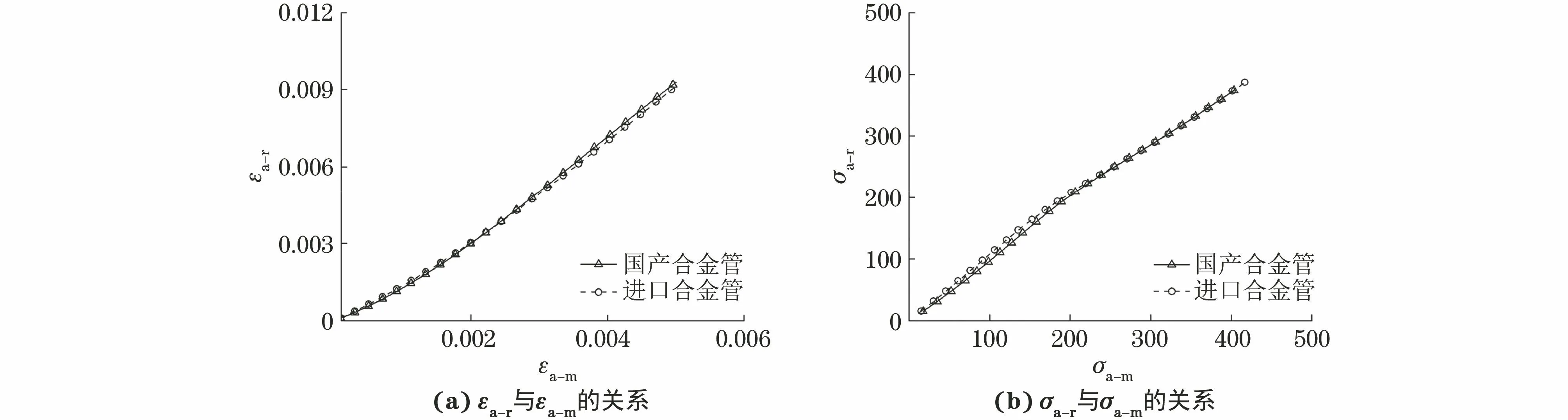
图7 国产和进口N06230合金管薄片漏斗试样的εa-r与εa-m以及σa-r与σa-m之间的关系Fig.7 Relations between εa-r and εa-m (a) and between σa-r and σa-m (b) of sheet-funnel specimens of domestic and imported N06230 alloy tubes
在高温低周疲劳试验的名义应变幅范围内,漏斗根部应力幅和应变幅与平均应力幅和名义应变幅之间的关系可简单采用多项式描述:
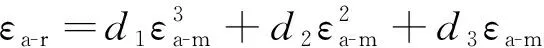
(15)

(16)
式中:d1,d2,d3,e1,e2,e3均为回归系数,拟合结果列于表3中。

表3 国产和进口N06230合金管薄片漏斗试样εa-r与εa-m以及σa-r与σa-m的多项式回归系数Table 3 Polynomial regression coefficients between εa-r and εa-m and between σa-r and σa-m
3.3 疲劳寿命预测
根据2种合金管的薄片漏斗试样低周疲劳试验获得的εa-m-Nf曲线,结合εa-r与εa-m及σa-r与σa-m之间的关系,将名义应变幅和平均应力幅转换为漏斗根部应变幅和应力幅,预测得到的疲劳寿命拟合曲线如图8所示,M-C模型参数列于表4中。由图8可知,在650 ℃条件下,当应变幅低于0.004 02时,国产合金管的疲劳寿命略高,而当应变幅高于0.004 02时,国产合金管的疲劳寿命略低。
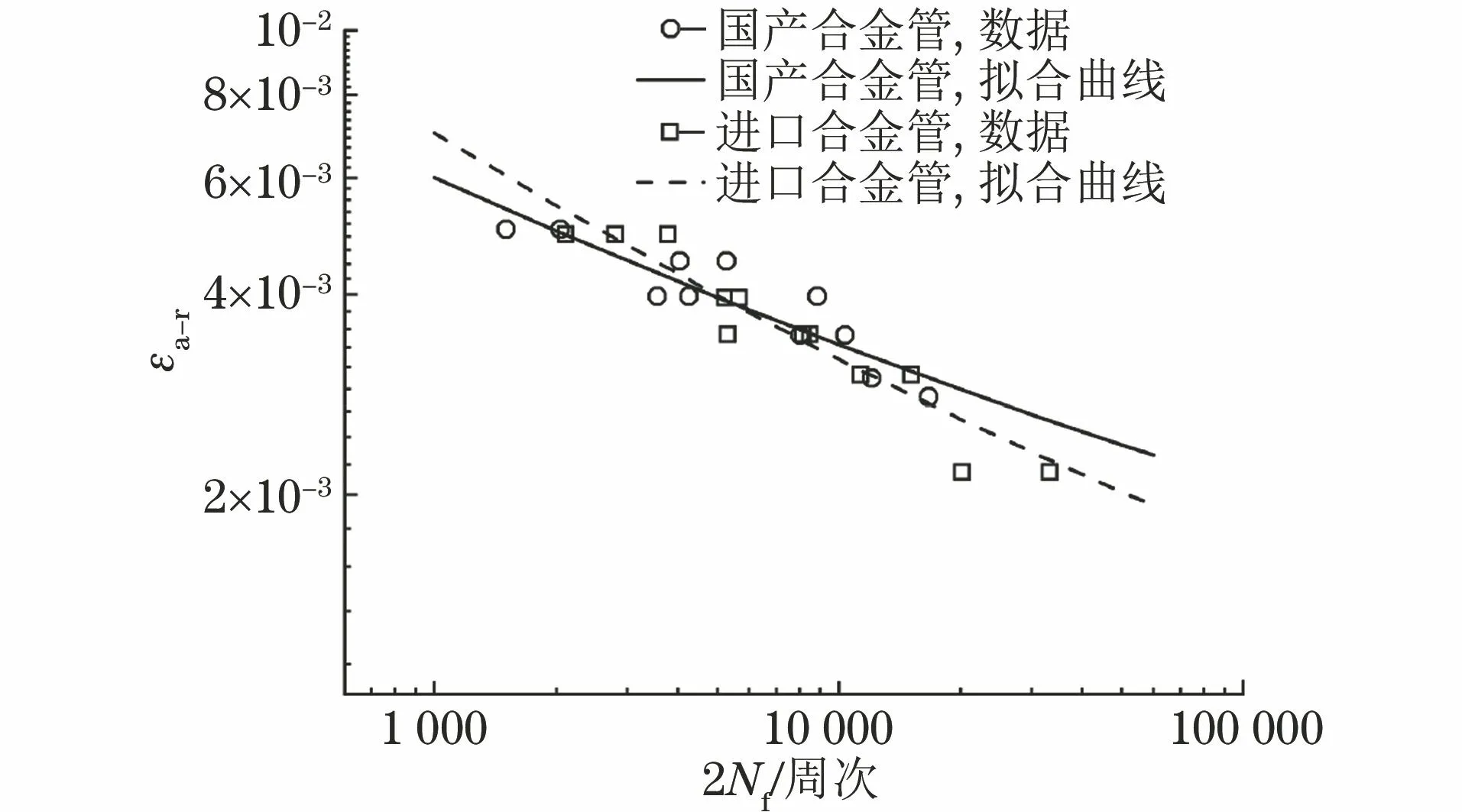
图8 国产和进口N06230合金管的疲劳寿命拟合曲线Fig.8 Fatigue life fitting curves of domestic and imported N06230 alloy tubes

表4 国产和进口N06230合金管的M-C模型参数Table 4 M-C model parameters of domestic and imported N06230 alloy tubes
4 结 论
(1) 根据薄片漏斗试样高温低周疲劳试验方法和确定的循环应力幅-应变幅关系参数模型常数,获得的应力幅-应变幅曲线与有限元分析预设的曲线相吻合,符合性优度均高于0.98,说明该模型对于预测材料循环应力幅-应变幅关系具有普适性和精确性。
(2) 国产N06230合金管的循环应力幅-应变幅曲线及高温低周疲劳性能与进口合金管相近;当应变幅低于0.004 02时,国产合金管的疲劳寿命略高,而当应变幅高于0.004 02时,国产合金管的疲劳寿命略低。
