对照“评价”搞研究 立足“课标”抓教学

陈小璐 徐永忠

2022年高考过去了，留给我们研究的东西很多，特别是数学卷．下面我们以立体几何问题做一点研究，以利于今后教学工作的有效开展．

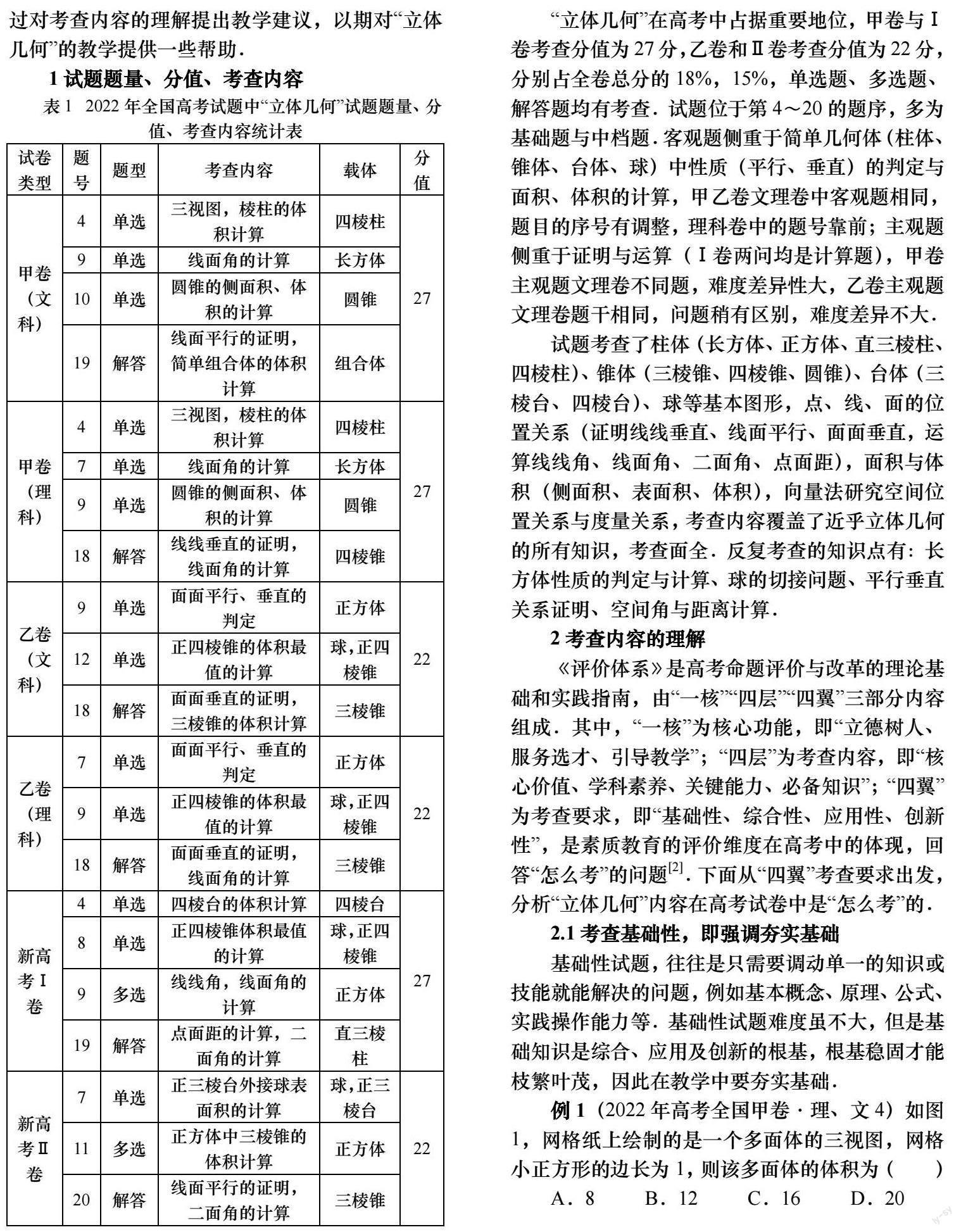
立体几何研究现实世界中物体的形状、大小与位置关系．高中立体几何学习有两个阶段：一是必修课程主题三中的立体几何初步，主要内容有认识和理解空间点、直线、平面的位置关系，平行、垂直的性质与判定，简单几何体的表面积与体积的计算；二是选择性必修课程主题二中的空间向量与立体几何，主要内容有运用向量的方法研究空间基本图形的位置关系和度量关系，体会向量方法和综合几何方法的共性和差异[1]．立体几何的学习有助于用数学的眼光观察世界，培养空间观念，实现几何直观与代数运算的融合．本文对照《普通高中数学课程标准（2017年版2020年修订）》（以下简称《课标（2020年修订）》）和《中国高考评价体系》（以下简称《评价体系》）研究2022年6套全国高考试卷中“立体几何”模块试题的题量、分值与考点，通过对考查内容的理解提出教学建议，以期对“立体几何”的教学提供一些帮助．

“立体几何”在高考中占据重要地位，甲卷与Ⅰ卷考查分值为27分，乙卷和Ⅱ卷考查分值为22分，分别占全卷总分的18%，15%，单选题、多选题、解答题均有考查．试题位于第4～20的题序，多为基础题与中档题．客观题侧重于简单几何体（柱体、锥体、台体、球）中性质（平行、垂直）的判定与面积、体积的计算，甲乙卷文理卷中客观题相同，题目的序号有调整，理科卷中的题号靠前；主观题侧重于证明与运算（Ⅰ卷两问均是计算题），甲卷主观题文理卷不同题，难度差异性大，乙卷主观题文理卷题干相同，问题稍有区别，难度差异不大．

试题考查了柱体（长方体、正方体、直三棱柱、四棱柱）、锥体（三棱锥、四棱锥、圆锥）、台体（三棱台、四棱台）、球等基本图形，点、线、面的位置关系（证明线线垂直、线面平行、面面垂直，运算线线角、线面角、二面角、点面距），面积与体积（侧面积、表面积、体积），向量法研究空间位置关系与度量关系，考查内容覆盖了近乎立体几何的所有知识，考查面全．反复考查的知识点有：长方体性质的判定与计算、球的切接问题、平行垂直关系证明、空间角与距离计算．

2 考查内容的理解

《评价体系》是高考命题评价与改革的理论基础和实践指南，由“一核”“四层”“四翼”三部分内容组成．其中，“一核”为核心功能，即“立德树人、服务选才、引导教学”；“四层”为考查内容，即“核心价值、学科素养、关键能力、必备知识”；“四翼”为考查要求，即“基础性、综合性、应用性、创新性”，是素质教育的评价维度在高考中的体现，回答“怎么考”的问题[2]．下面从“四翼”考查要求出发，分析“立体几何”内容在高考试卷中是“怎么考”的．

2.1考查基础性，即强调夯实基础

基础性试题，往往是只需要调动单一的知识或技能就能解决的问题，例如基本概念、原理、公式、实践操作能力等．基础性试题难度虽不大，但是基础知识是综合、应用及创新的根基，根基稳固才能枝繁叶茂，因此在教学中要夯实基础．

例1（2022年高考全国甲卷·理、文4）如图1，网格纸上绘制的是一个多面体的三视图，网格小正方形的边长为1，则该多面体的体积为（ ）

A．8 B．12 C．16 D．20

3教学建议

高考试题的研究不仅对高三复习有价值，对高一、高二年级初学立体几何及相关知识时也有很大的指导作用，所以我们必须站在一定的高度开展教学和复习工作．

3.1注重基础，落实课程标准

高考要求“全面考查基础知识”，《课标（2017版）》中的基本知识在复习过程中要全面覆盖，不留死角．不仅要关注高考重点问题、热点问题，冷门问题也要关注，例如2022年全国高考试题未考查的有动态几何问题、四点共面问题、开放型问题等．课程标准中提出要体会向量方法和综合几何方法的共性和差异，理解如图9．

要站在系统的角度看待立体几何教学与复习，不能考什么就教什么、复习什么，新高考没有考试说明了，对于我们的教学参照只有《课标（2020年修订）》与教材．《课标（2020年修订）》上列出的考试三级指标，就是我们应该对照的教学要求．

3.2 关注能力，提升核心素养

数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，立体几何知识的学习有助于提升直观想象、逻辑推理、数学运算素养．高考试题对学生的考查不仅是侧重基础知识的理解，更是侧重对学科素养的考查[3]． 立体几何的客观题需要作出图形，借助图形转化、解决问题，因此在教学过程中应培养作图能力，提升直观想象素养；主观题包含证明与运算，证明问题中定理内容需表达清晰，各步骤之间需逻辑准确，因此在教学过程中应提升逻辑推理素养；运算涉及体积与面积公式，空间向量法中线面角、二面角、点面距的向量公式，综合法作图平面化后求解三角形时正弦定理、余弦定理公式等，因此在教学过程中需提升数学运算素养． 另外，对于一些重要的结论、公式等的教学，一定要让学生有体验的时间和经历，也就是注意基本经验的积累，以减少死记硬背带来的失误．如2022年全国新高考1卷第20题的第一问，侧重学科素养的考查，没有直接考查三棱锥的体积公式，而是考查了三棱锥与同底等高三棱柱的关系，不少学生就将这个关系记成了二分之一，导致本题失误．学生初次学习这个概念是小学六年级，后来初中遇到就运用一下，到高中如果我们的教学对它们之间的关系只是一带而过，要求学生记住三棱锥体积公式，沒有让学生认真经历它们之间关系的推导过程，高考时学生记错关系（公式）就不难理解了．所以《课标（2020年修订）》中新增加的“基本活动经验”非常重要，应在平时的教学中加以落实． 3.3 渗透文化，彰显核心价值

核心价值是指即将进入高等学校的学习者应当具备的良好政治素质、道德品质和科学思想方法的综合，主要包括“政治立场和思想观念、世界观和方法论、道德品质和综合素质”3个一级指标和10个二级指标．“政治立场和思想观念”包含理想信念爱国主义情怀等方面的基本要求[2]．高考试题融合了中国古代数学文化与社会主义现代文明，注重考查数学文化素养．2018年全国Ⅲ卷中将中国古建筑中的榫卯结构与“立体几何”中的俯视图相融合，2019年全国新课标Ⅱ卷（理科）将中国悠久的金石文化与“立体几何”中的面数、棱长问题相融合，2020年全国Ⅰ卷将中国古代测量时间的仪器“日晷”与“立体几何”中的球、线面垂直、线面角问题相融合，2022年全国Ⅰ卷将我国重大的建设成就“南水北调”工程与“立体几何”中的棱台问题相融合．古代数学文化的融合，有助于弘扬中华优秀传统文化，厚植爱国主义情怀，促使学生认同中华文化．社会主义现代文化的融合，有助于增强中国特色社会主义道路自信、文化自信，促使学生勇于奋斗与担当，肩负起实现中华民族伟大复兴中国梦的时代重任！ 4结语立体几何是高中数学核心内容之一．教学过程中应注重以试题为载体，指导学生善用基本图形锻炼空间想象能力，强化核心知识的理解与应用，引导学生不断优化解题路径，整体把握知识结构，理解命题体系，提升数学核心素养．

参考文献

[1]中华人民共和国教育部．普通高中数学课程标准（2017年版）[S]．北京：人民教育出版社，2018

[2]教育部考试中心．中国高考评价体系[M]．北京：人民教育出版社，2019

[3]葛丽婷，郭玉锋，郎春雨．近十年高考立体几何试题直观想象素养考查研究：表现及趋势[J]．数学通报，2021，60（11）：41-48

（本文系江苏省基础教育前瞻性教学改革试验项目“数学写作提升核心素养的实践研究”（项目编号：2020JSQZ0147）的阶段成果）