含双腐蚀缺陷高钢级油气管道剩余强度研究

申玉健

(中国石油天然气股份有限公司华北油田分公司 河北 沧州 062550)

0 引 言

在管道运行的过程中,受土壤腐蚀、介质腐蚀和大气腐蚀的影响,管道表面会发生壁厚减薄现象,在载荷的作用下,缺陷部位会产生应力集中,进而影响管道的承压能力,严重时泄漏气体还会引发喷射火、闪火或蒸汽云爆炸等不良后果[1-2]。因此,对含腐蚀缺陷管道的剩余强度和剩余寿命进行计算和评价显得尤为重要。

目前,已有大量学者对管道剩余强度进行了研究,常用的评价方法有ASME B31G标准系列、C-Fer法、DNV-RP-F101规范和PCORRC法等[3],这些方法基于断裂力学和爆破试验数据拟合得到,具有一定的科学性,但均以含单腐蚀缺陷的中低强度钢为研究对象,仅有DNV-RP-F101规范给出了相邻腐蚀缺陷的相互作用判定依据,并对腐蚀缺陷组合长度和组合深度的计算进行了细化。在实际的开挖和维抢修作业中发现,缺陷位置、缺陷尺寸和缺陷间距通常具有一定的随机性和不确定性,对于两个或两个以上的相邻腐蚀缺陷,由于缺陷间距较近,其破坏模式和失效形式往往较单腐蚀缺陷更加复杂。崔铭伟等[4]对比了不同相邻腐蚀管道的剩余强度评价方法,但未对相互作用判定准则进行修正;孙明明等[5-6]研究了环向对齐和等效不规则双腐蚀缺陷的管道失效压力,但文中限定的工况过于特殊;陈飞[7]对X80管道的双腐蚀缺陷的相互作用规律进行了研究,但没有给出剩余强度的计算方法。目前,X100钢的投产应用是今后管道建设的发展方向[8-10],因此研究X100钢的腐蚀缺陷剩余强度属于前瞻性研究,具有一定的必要性。杨燕华等[11]虽然对X100钢的剩余强度进行了敏感性分析,但没有给出双腐蚀缺陷的极限作用距离;国外研究学者的研究对象多为X80及以下钢级[12-13]。基于此,通过Workbench平台建立X100钢的轴向和环向双腐蚀缺陷,考察缺陷长度、缺陷深度和缺陷间距对高钢级剩余强度的影响,并以单腐蚀缺陷评价方法为基础,构建双腐蚀缺陷剩余强度评价方法。研究结果可为高钢级管道力学性能的评估提供实际参考。

1 有限元分析可靠性验证

1.1 模型设置

有限元分析法是目前应用较多的用于管道剩余强度安全评价的方法,其计算结果与真实水压爆破实验值基本一致,已被诸多学者证实其准确性和科学性[4,7,11]。采用Solidwork软件建立管道模型,并将其导入Workbench平台,管道尺寸为Φ1 320 mm×22.9 mm,力学性能参数见表1。

表1 管道力学性能参数

采用Ramberg-Osgood方程模拟真实的应力-应变曲线,见公式(1)和图1。选取最具代表性的矩形缺陷为研究对象,为避免分析时产生应力集中,将缺陷边界进行圆角处理。

图1 X100钢的真实应力-应变曲线

(1)

式(1)中:εture和σture分别为真实应变和真实应力;σu,ture为实际的极限拉伸强度, MPa;E为弹性模量, MPa。

1.2 边界条件设置和网格划分

为提高计算速度,采用1/2的管道模型,分别在管道轴向端面和对称剖面上施加位移约束和无摩擦约束,内壁上只考虑压力载荷对等效应力的影响。为排除圣维南效应带来的端点作用,管道长度取2.5 m。

为细化描述缺陷处的参数,采用三维八节点积分单元对网格进行划分,如图2所示。

图2 网格划分情况

1.3 失效准则

考虑到高等级钢具有良好的韧性,基于Von Mises的等效应力在弹性极限准则和塑性极限准则上的应用较为保守,故在此使用塑性失效准则,即当管道的最大应力超过极限抗拉强度(886 MPa)时,此时施加的内压载荷即为剩余强度。Von Mises应力失效准则公式如下[14-15]:

(2)

式(2)中:σM为Von Mises等效应力, MPa;σ1、σ2、σ3分别为3个方向上的主应力, MPa。

1.4 模型验证

考虑到双腐蚀缺陷的剩余强度是以单腐蚀为基础,因此收集文献中的单腐蚀实验数据[16-18],进行有限元分析,并与其余评价方法结果进行对比,见表2。表2中,D为管道外径;t为壁厚;L为缺陷长度;d为缺陷深度。有限元分析结果的相对误差范围为0～1.98%,平均相对误差在所有评价方法中最小为1.01%,说明建立的非线性有限元模型可以较好地反映X100钢腐蚀管道的剩余强度,模型在边界条件、材料性能和载荷约束上的设置较为合理,可以作为后续双腐蚀缺陷的研究手段。

表2 不同方法计算结果误差

2 结果与分析

根据以往研究[5,8],缺陷宽度对管道力学性能的影响较小,故在此只考察不同缺陷长度、缺陷深度和缺陷间距对管道剩余强度的影响。为便于分析,采用无量纲化参数描述腐蚀特征,分别为腐蚀深度系数k1、腐蚀长度系数k2、相邻腐蚀轴向间距系数n、相邻腐蚀环向间距系数c等,公式如下:

(3)

式(3)中:SA为相邻腐蚀轴向间距,mm;θ为相邻缺陷夹角,(°)。利用控制变量法,在有限元分析模块中施加不同强度的内压,观察腐蚀缺陷处的最大等效应力和剩余强度的变化情况。

2.1 双腐蚀缺陷轴向分布

保持双腐蚀缺陷在同一轴线上,考虑到现场中的管道缺陷多为短缺陷,即k2=1,故在该条件下,考察施加内压载荷与最大等效应力之间的关系,如图3所示。当内压较小时,管道首先进入弹性阶段,缺陷处的等效应力呈直线上升;随后,管道达到屈服阶段,此时缺陷处的应力增加很少;最后,随着内压的增加,管道进入强化阶段,当最大等效应力等于管道极限抗拉强度时,管道发生破裂。在缺陷深度较浅时,不同缺陷轴向间距下的最大等效应力几乎一致;在缺陷深度较深时,缺陷轴向间距越大,对应的最大等效应力越小。

图3 不同k1和n下内压载荷与等效应力的关系(k2=1)

考察不同腐蚀长度、腐蚀深度在n值变化时对管道剩余强度的影响,如图4所示。剩余强度随着n值的增加而增大,最后趋于稳定。当n值较小时,双腐蚀作用下的剩余强度远小于单腐蚀单独作用于管道,此时缺陷间的相互作用对剩余强度产生较大影响,内应力沿缺陷长轴对称分布,最大应力位于双腐蚀缺陷的轴向中间区域;当n值较大时,缺陷间的相互作用逐渐减弱,最大应力从双腐蚀缺陷的轴向中间区域转移到缺陷内部,此时管道剩余强度等于单腐蚀缺陷单独作用于管道。腐蚀长度系数k2越大,管道剩余强度越小,且这种减小趋势越来越小;腐蚀深度系数k1越大,管道剩余强度越小,且这种减小趋势越来越大,证明了腐蚀深度对管道失效压力的影响较大。

图4 轴向腐蚀缺陷参数对剩余强度的影响

2.2 双腐蚀缺陷环向分布

保持双腐蚀缺陷在同一环向上,在腐蚀长度系数k2=1的条件下,考察管道内压载荷与等效应力之间的关系,如图5所示。按照θ从0°到180°换算(步长20°),共得到7个环向间距系数c,分别为0、0.63、1.26、1.89、2.53、3.16、3.79。与双腐蚀缺陷轴向分布的应力变化结果一致,随着内压的增加,管道的变形发展先后经历了弹性、屈服和强化阶段,不同环向间距下的最大等效应力几乎不发生变化。此外,对比图3和图5,相同腐蚀深度下,缺陷轴向分布的最大等效应力要大于缺陷环向分布,因此双腐蚀缺陷在轴向分布时的危险系数更高。

图5 不同k1和c下内压载荷与等效应力的关系(k2=1)

考察不同腐蚀长度、腐蚀深度在c值变化时对管道剩余强度的影响,如图6所示。剩余强度随着c值的增加而增大,最后趋于稳定。当腐蚀深度不变时,腐蚀长度越长,管道剩余强度越小,且这种减小趋势越来越大;当腐蚀长度不变时,腐蚀深度越大,管道剩余强度越小,且这种减小趋势越来越大。此外,对于环向缺陷,只有在腐蚀长度较长时,c值的变化对剩余强度较敏感,而腐蚀深度的变化对剩余强度不敏感。

图6 环向腐蚀缺陷参数对剩余强度的影响

2.3 剩余强度公式拟合

通过表2观察,对于单腐蚀缺陷,除有限元分析法外,DNV-RP-F101规范的预测结果相对误差最小,故以该方法为基准进行修正,公式如下:

(4)

(5)

p=pf+b1k1b2·k2b3·nb4·cb5

(6)

式(6)中:p为双腐蚀缺陷作用下的剩余强度, MPa;pf为单腐蚀缺陷的剩余强度, MPa;σu为极限拉伸强度, MPa;M为当量长度系数;b1～b4为待定系数。当双腐蚀缺陷为轴向分布时,公式(6)中的cb5项不存在,当双腐蚀缺陷为环向分布时,公式(6)中的nb4项不存在。

对公式(6)的参数进行拟合,通常将其变形为下式:

p-pf=b1k1b2·k2b3·nb4·cb5

(7)

两边取对数后:

ln(p-pf)=lnb1+b2lnk1+b3lnk2+b4lnn+b5lnc

(8)

随后,对公式(8)进行线性替换,通过最小二乘法即可得到待定系数。但从公式(6)向公式(8)转换时,所求待定参数的最小二乘估计是基于公式(8),而非公式(6),两者存在数据不同源的现象。因此,采用1stopt软件对公式(6)进行多元非线性拟合,选择差分进化法、最大继承法、遗传算法、模拟退火算法、下山单体法、自组织群移法、共扼梯度法,设置最大迭代次数1 000,实际输出控制数20。通过对比多种全局优化算法,不同优化算法的迭代次数和寻优精度有所不同,其中模拟退火算法在限定迭代次数内的精度最高,故采用模拟退火算法求解待定参数。

缺陷轴向分布的拟合公式为:

(9)

缺陷环向分布的拟合公式为:

(10)

从b1的拟合结果可知,双腐蚀缺陷的剩余强度要小于单腐蚀缺陷的剩余强度,且缺陷轴向分布对腐蚀深度参数敏感,缺陷环向分布对腐蚀长度参数敏感,与前述的研究结果一致。将公式(9)～(10)的本文算法与DNV-RP-F101规范的计算方法对比,拟合结果如图7所示。可见,本文算法与有限元分析结果的吻合性更好,数据基本分布在回归线附近,相对误差更小,而DNV-RP-F101规范的计算结果大部分大于有限元分析结果,存在一定的不安全因素。

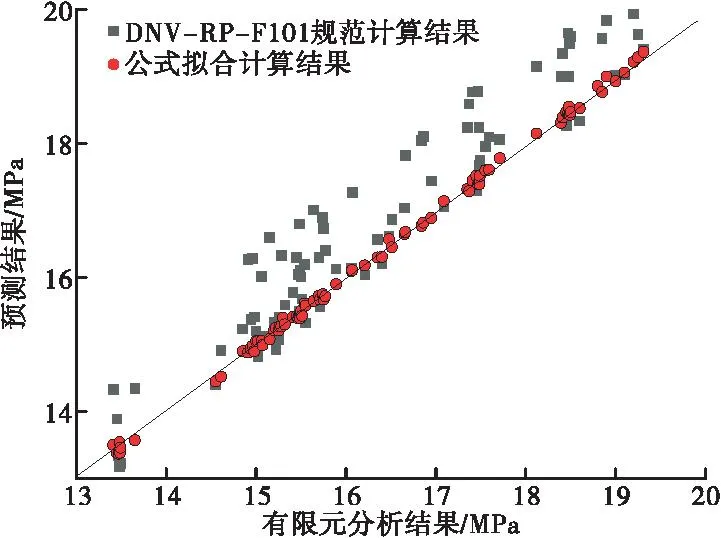
图7 剩余强度拟合结果

3 结 论

1)随着内压的增加,管道先后经历了弹性阶段、屈服阶段和强化阶段,在缺陷深度较深时,轴向间距对缺陷轴向分布时的最大等效应力影响较大;不同环向间距下的最大等效应力几乎不发生变化。

2)当n=2.5、c=1.26时为双腐蚀缺陷的极限作用距离,小于这个距离时,需考虑腐蚀缺陷间的相互作用和影响;大于这个距离时,按照单腐蚀缺陷计算管道剩余强度。

3)在DNV-RP-F101规范的基础上,修正了双腐蚀缺陷剩余强度评价方法,并通过全局优化算法确定待定参数,其计算结果精度较高,说明该方法具有较好的可靠性和科学性。

4)今后可进一步针对含内外双腐蚀缺陷、多点腐蚀缺陷、不规则腐蚀缺陷的管道剩余强度进行评价,完善高等级钢的力学特征分析。