埋地压力钢管结构计算规律分析

2023-09-12吴国茂

水利规划与设计 2023年9期

吴国茂

(遵义市水利水电勘测设计研究院有限责任公司，贵州遵义 563002)

0 引言

在水库、引调水、给排水工程中，多数为输水管道，在高水头、跨公路、减小占地、经济环保及复杂地形等输水埋地钢管使用越来越高。国内埋地管设计及理论最先在给排水设计规范[1]中，由于水利水电行业通常水头内水压力高，罗加谦等[2]通过某工程高水头埋地压力钢管设计研究，为后续高水头埋地管道设计提供了的依据；石长征等[3]通过给排水规范中埋地钢管的公式，将其中极限状态设计方法改为原水利水电钢管设计规范的允许应力法，得到计算结果与国外规范相接近，说明此法在水利水电行业设计中具有较好的适用性，值得进一步的探讨；伍鹤皋等[4]针对内压对回填钢管有复圆作用，对管底弯矩影响较大，在弯矩计算公式中加入内水压力项计算内水压力对弯矩的影响，随后纳入水利行业钢管设计规范[5]，使埋地钢管的结构计算理论在水利水电行业越来越成熟；段正刚等[6]针对现阶段钢管设计规范编制了结构计算及程序；张发茂等[7]通过回填刚性管和柔性管两种模型对比分析得出刚性钢管按柔性钢管计算是安全的，水利规范的允许应力法与给水钢管规范的极限状态设计方法对比得出二者计算结果基本相当；伍鹤皋等[8]基于正交试验法对埋地钢管参数敏感性进行分析，得到回填土和垫层的变形模量是影响埋地钢管结构的最主要因素，而沟槽的形态也对钢管结构产生较大的影响；陈万波等[9]针对埋地钢管变形公式系统规律分析，得到钢管的最大允许埋深与管侧土变形模量Ed和D/t的关系，在水重作用下钢管变形会加大，水压作用下钢管变形会大幅度的复圆，而高Ed约束作用下能够部分削弱水压的复圆效果；徐春峰等[10]认为埋地管道强度、刚度及抗浮刚度不要求，选择换管侧埋置土或砼包管比增加管道壁厚更合适。杨晓蕾等[11]利用给排水规范公式得到管底弯曲环向应力最大时与D/t的函数关系。现阶段研究者们只是针对某工程或某公式进行分析，没有系统深入对各公式中应力与各参数之间、各工况之间的相互关系进行分析，为了解决设计者困惑，提高设计理论水平，本文通过系统分析，得到回填压力钢管计算的相关规律。

1 埋地钢管结构计算相关公式

根据水利水电工程压力钢管设计规范[5]有：

(1)

(2)

(3)

Fv=Fso+Ft=γtHsoD1

(4)

(5)

式中，P—内水压力；r—钢管半径；t—钢管壁厚；K、K1、K2—与管底土弧中心角有关的系数；Ed—管侧土综合变形模量；Es—钢材的弹性模量；Fv—管顶竖向荷载；Gw—单位长度管道内水重；Gst—单位长度管道自重；M1—各荷载在管底引起的弯矩；σb1—管底环向弯曲应力；σθ—总环向弯曲应力；Hso—管顶埋深；Pt—单个轮压；pv—放空时内外压差；pe—管道外压；pk—钢管临界外压。

总体来说，埋地管影响主要因素有t、r、P、θ、Ed、Hso、Pt、ΔTS，文中主要针对这些参数进行分析。

2 正常运行工况下应力与各参数关系

2.1 管底环向弯曲应力、总环向应力与壁厚、半径关系

将公式(1)带入(2)得到

(6)

设各参数见表1。

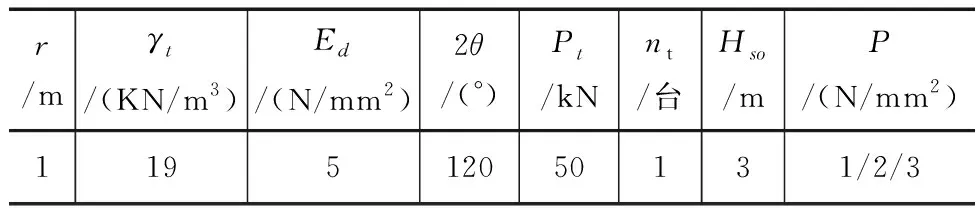
表1 各参数设定值

不同壁厚t与总环向弯曲应力、总环向应力的关系如图1—2所示。从图1—2可以看出，随着壁厚t增加，管底环向弯曲应力σb1先增大后减小，总环向弯曲应力σθ整体出现减小趋势，但在较低水头下，出现与σb1相近的规律，原因是低水头下产生的环向应力太小不足以改变σb1的规律，得到与σb1相近的规律；在不同内水压力P作用下，P越大，σb1越小，而σθ越大，说明当内水压力增加时，可以减小σb1，相应对σθ有减小作用，但内水压力的增加对σθ增加幅度大，因此总体上σθ呈增大趋势。

图1 不同内水压下环向弯曲应力σb1与壁厚t关系

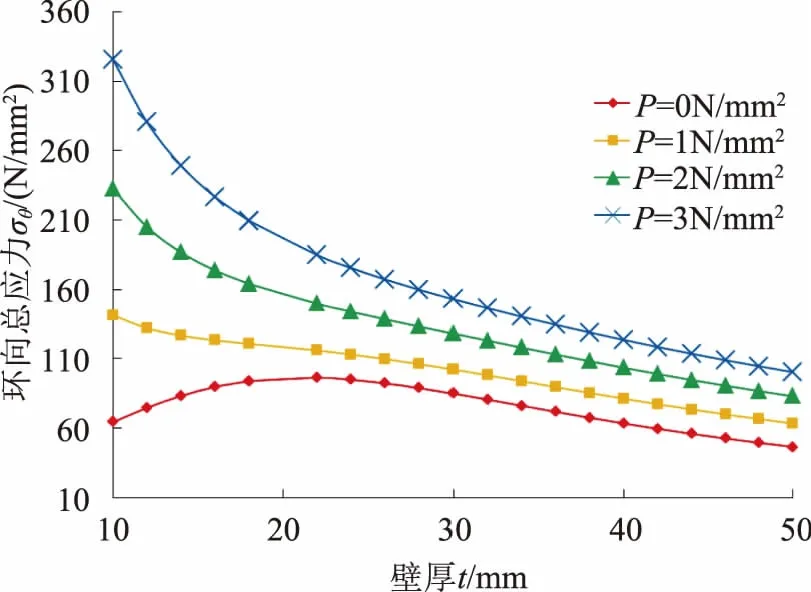
图2 不同内水压下总环向应力σθ与壁厚t关系

在不考虑管道自重Gst中壁厚t的影响下，对公式(2)管底环向弯曲应力σb1中壁厚t求导，得到计算公式如下：

(7)

可以通过公式(7)计算最大弯曲应力σb1对应的壁厚t，当为管内充水或放空工况时，即不考虑内水压力P的作用得到最大弯曲应力σb1对应壁厚t。

当同时变化壁厚t、半径r情况时，其他参数见表1，得到总环向应力σθ如图3—4所示规律。

图4 P=1.0N/mm2总环向应力σθ与t、r关系

从图3—4中可以看出，相同t的情况下，随着r的增加，σb1先增大后减小，σθ呈增大趋势。通过变化内水压P、Ed和管底土弧中心角θ下，环向弯曲应力σb1最大时，t/r一般在1/30～1/80之间。

2.2 管底引起环向弯曲应力与管底土弧中心角的关系

通过图5对比分析不同管径得到，管底弯曲应力σb1与土弧中心角2θ的呈反相关关系。随着2θ增大而迅速减小，当2θ=180°时，弯曲应力最小；当2θ=60°时，弯曲应力比(弯曲应力与最小弯曲应力比)约为1.42；当2θ=90°时，弯曲应力比约为1.20；当2θ=120°时，弯曲应力比约为1.08；当2θ=150°时，弯曲应力比约为1.02，因此2θ在90°～120°之间时，是较为经济安全的角度范围。

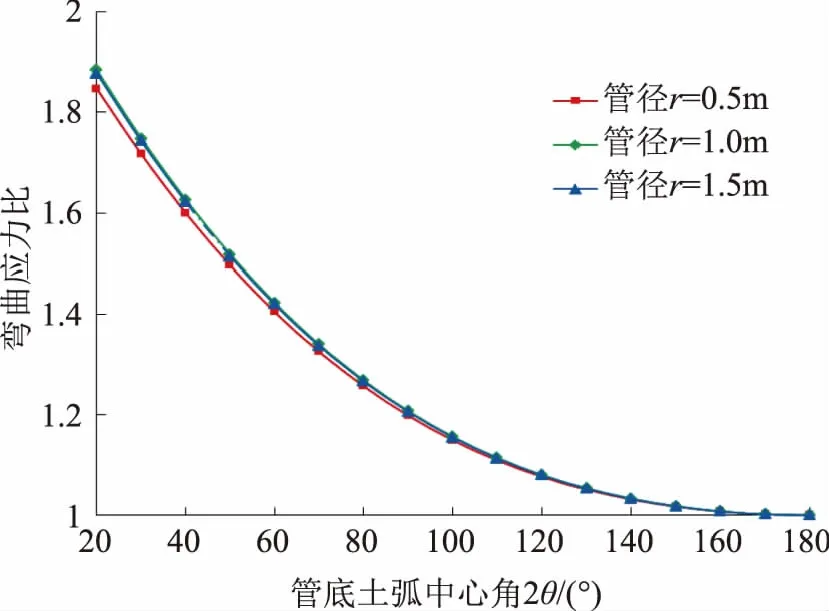
图5 不同管径下环向弯曲应力比与管底土弧中心角的关系

2.3 管底环向弯曲应力与埋深+车辆荷载关系

根据计算公式(2)、(4)可以看出，当无车辆荷载Pt时，弯曲应力σb1与埋深Hso为线性关系；当有车辆荷载Pt作用需要通过分析，设汽车单个车轮轮压Pt分别为10、30、50、100KN，其他参数见表1，可分别得到不同Hso+Pt下，与σb1的关系，如图6所示。

图6 不同车辆荷载下环向弯曲应力与埋深关系

通过图6分析得到在有汽车荷载情况下，当埋深Hso较小时，环向弯曲应力较大；随着埋深增加，底部环向弯曲应力先减小后增大；当埋深Hso≥3m时，汽车荷载的变化对环向弯曲应力影响较小；在汽车荷载下埋深1～2m之间，环向弯曲应力σb1最小，管径较小时取大值。

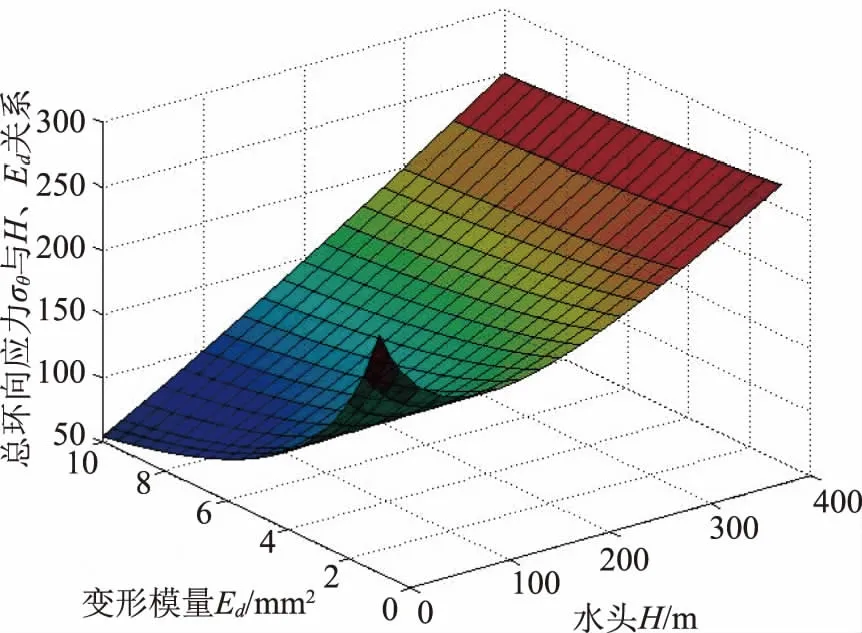
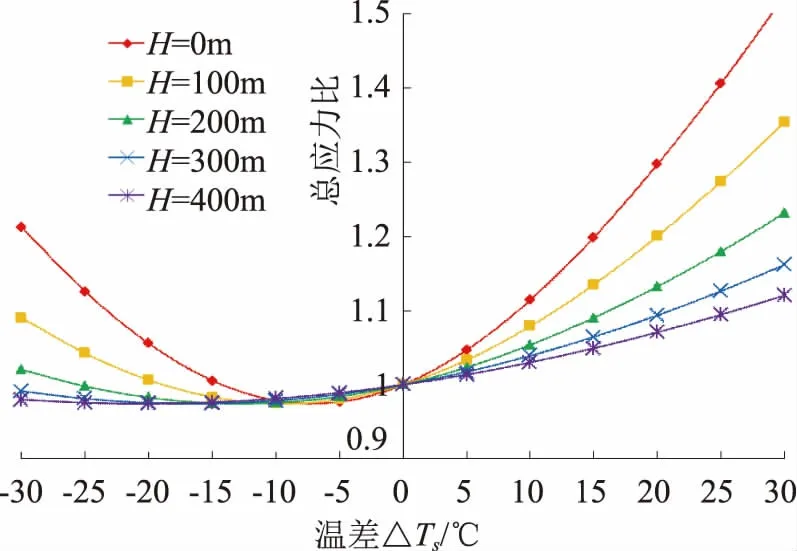
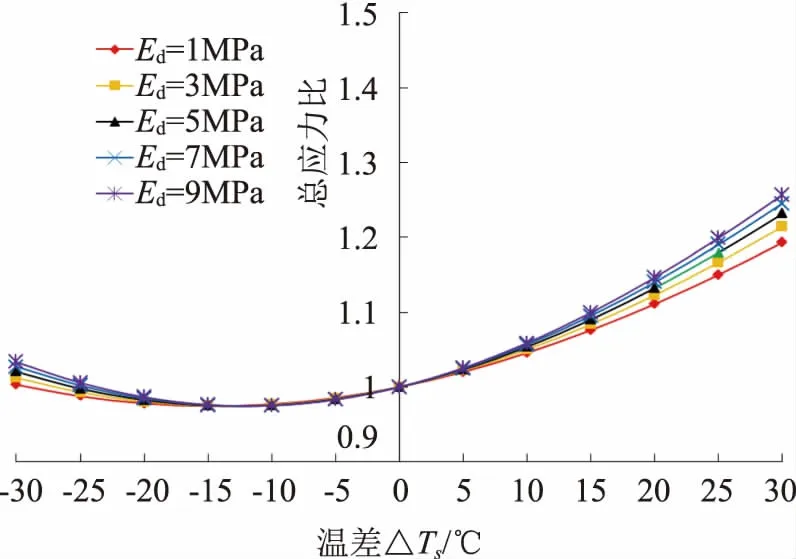
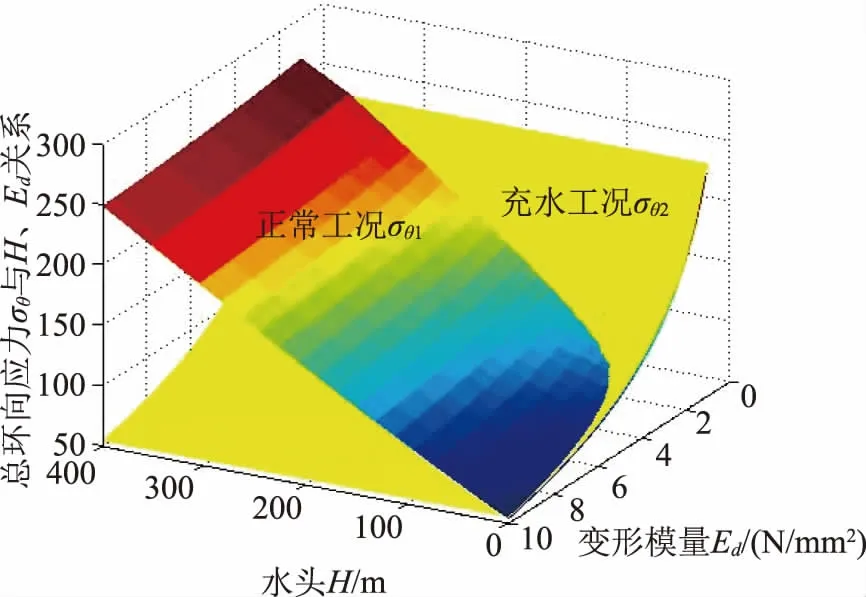
此外，通过对公式Ft=WtD1进行分析，当a+2Hsotanφ

(8)

修正后得到管底引起环向弯曲应力σb1与埋深的关系如图7所示，通过对比分析，埋深较浅段修正后的弯曲应力有明显减小。

图7 不同车辆荷载下环向弯曲应力与埋深关系(修正后)

2.4 管底环向弯曲应力、总环向弯曲应力与内水压、管侧土变形模量关系

给排水规范[1]环向弯曲应力σb1未考虑内水压P作用，水利钢管设计规范[5]中考虑了P后，管底环形弯曲应力σb1有减小作用，总体上环向弯曲应力σθ与水压P(P=0.01H，H为水头)是反相关关系；环向弯曲应力σθ与内水压P是正比例关系；结合表1的除管经外参数(r=1.5m时t=24mm)，在变化管侧土变形模量Ed的情况下，得到总环向应力σθ与H、E关系如图8—9所示。