一种钻井指向式导向机构的力学分析*

刘 昌,陈雪菲,程为彬,李 锐,胡少兵,吕姜辉

(1. 长江大学地球物理与石油资源学院 湖北 武汉 430100; 2.长江大学电子信息学院 湖北 荆州 434023)

0 引 言

动态指向式旋转导向钻井工具具有导向能力强、钻井效率高和井眼光滑等优势,但对钻井工具的稳定性、控制精度和井眼位置的控制等提出了更高的要求[1]。导向装置是旋转导向钻井系统的核心部分,是实现调整钻头轨迹方向的关键结构,对导向机构的力学分析进行研究,可为自主研发指向式旋转导向机构提供一定的设计基础。尹福来通过建立偏置芯轴动力学模型,对其能量、稳态动力学和扭转耦合动力学等问题进行研究[2];杨磊和冯定等人建立导向工具的力学模型,推导出各个参数的计算公式,分析各个参数对导向轴的影响[3-5];李洪涛通过拉格朗日方程建立微分方程,考虑阻尼和传动比等因素分析导向机构的力学模型[6];张红和张光伟建立了外壳、主轴的关系式和力学模型,分析了偏置力关于各个参数的表达式[7-9]。上述研究采用单一的方法进行分析,存在力学模型建立不精确的问题,可能导致模型分析出现误差。

本文通过纵横弯曲法[10-11]和有限元法[12-16]建立力学模型,建立外壳与导向轴的挠度曲线方程,分析影响导向装置偏置能力的相关因素。

1 导向机构及其工作机理

静态指向式旋转导向机构的设计如图1所示,采用单偏心环偏置导向轴,改变偏置角度大小,通过后关节旋转改变偏置角度的方向,单偏心环偏置角度与关节旋转角度的矢量合成角度为导向角度。偏心环由中空旋转台和伺服电机带动,中空旋转台可以减速增矩,偏心环旋转时会给导向轴一个偏置力,从而偏置导向轴。后关节采用中空旋转台和伺服电机进行驱动,通过球形万向节带动前关节旋转,从而使钻头朝指定方位进行偏转。

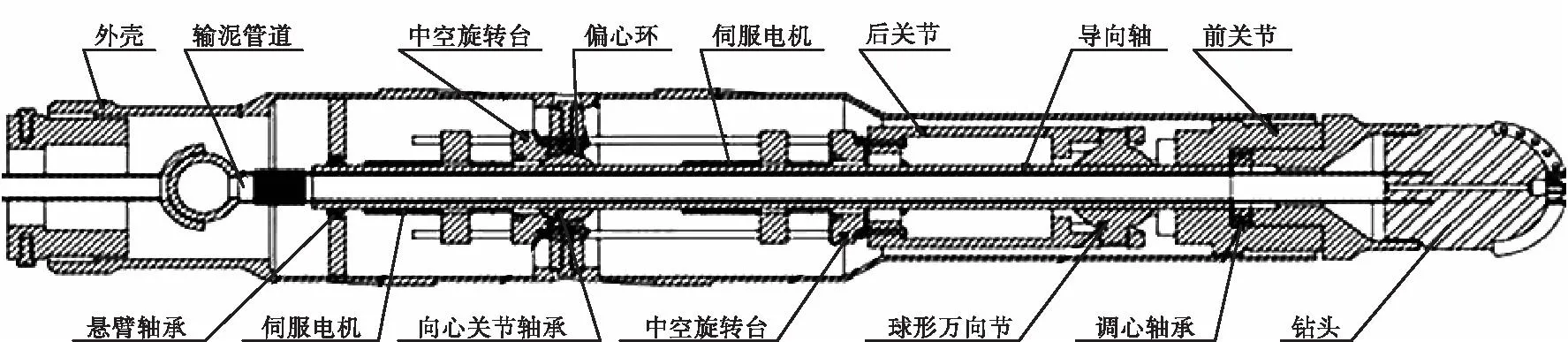
图1 指向式旋转导向机构样机设计图

导向功能调节如图2所示,当处于稳斜状态时,导向轴偏置钻头,使钻头达到预设角度,后关节处于静止状态;当处于造斜状态时,通过电机驱动偏心环,偏置钻头达到预设角度,再通过后关节旋转,调节偏置的方向,从而达到按预设方向偏置不同角度的要求[17]。

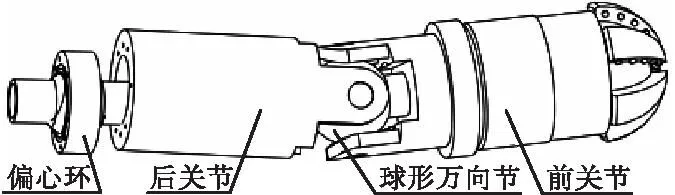
图2 导向功能调节示意图

2 关键结构动力学分析

2.1 导向轴力学建模

综合考虑单偏心环、悬臂轴承和调心滚子轴承等因素,建立指向式旋转导向工具井斜平面主轴与外壳的静力学模型,如图3所示。

图3 导向轴力学模型

以调心轴承中心为参考系的原点O建立坐标轴。L为远钻端悬臂轴承与近钻端调心滚子轴承之间的间距,m;L1为单偏心环与近钻端调心滚子轴承之间的间距,m;L2为单偏心环与远钻端悬臂轴承之间的间距,m;F为单偏心环偏置导向轴的偏置力,N;B为主轴作用点,C为外壳作用点。

根据力平衡方程和力矩平衡方程,可以得到导向轴和外壳在偏心环处的变形与转角关系。

1)导向轴挠度曲线方程:

(1)

式中:E1为导向轴的弹性模量,Pa;I1为导向轴的截面惯性矩,m4。

2)外壳挠度曲线方程:

(2)

式中:E2为外壳的弹性模量,Pa;I2为外壳的截面惯性矩,m4。

根据作用力与反作用力,导向轴与外壳在B、C点所受的径向力相等,故由上述方程可知B、C点的挠度方程。挠度关系ωB+ωC=e,式中e为偏心距。 将B、C点挠度方程和挠度关系式合并,可得偏心环处的偏置力F。

(3)

根据挠度曲线和位移的微分关系,可以得到导向轴上任意一点的微分函数,即可求得导向轴近钻段偏转角θ0。

(4)

2.2 向心关节轴承应变应力分析

根据牛顿第三定律可知,导向轴对向心关节轴承的作用力F1与偏置力F等大反向,因此:

(5)

造斜时,偏心环处于旋转状态,此时向心关节轴承可以等效为一个环形结构,内环受到导向轴施加在向心关节轴承的力F3。选取任意一个时刻,对其瞬态进行受力分析,该单元节点位移有8个自由度,如图4所示。在节点上的位移可组成一个矩阵qe;在节点上的力可组成一个矩阵Fe。

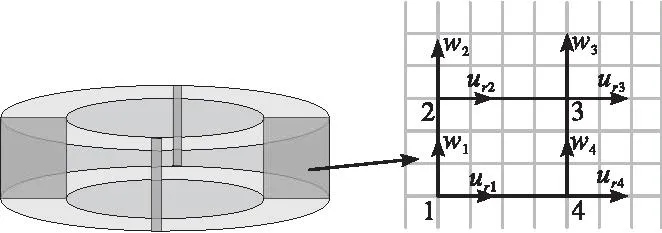
图4 偏心环等效图及单元节点矩形图

导向轴与向心关节轴承接触可看作线接触,即单元截面受到一个均布载荷,大小为F1,所以矩阵Fe也可以表示节点力。

偏心环是轴对称结构,没有环向位移,只有径向应力σr、轴向应力σz和剪应力τrz,其中τrθ,τzθ均为0。3个应力对应的3个应变分量分别为εr、εz和γrz。

通过单元位移函数和几何方程,可以得到单元应变表达式:

(6)

式中:B为应变矩阵。

将应变分量的物理方程改成应力分量的物理方程:

(7)

式中:D为轴对称弹性矩阵。

将应变表达式代入物理方程中可得:

(8)

式中:S为应力矩阵。

由虚功原理,求解刚度矩阵Ke:

(9)

则该系统的刚度方程为:

(10)

3 数值模拟计算与结果分析

3.1 材料参数配置

导向结构外壳采用材料为合金结构钢35CrMoV,材料性能见表1,其外径D1=218 mm,内径d1=208 mm,极惯性矩I1=3.797 0×107m4;偏心环材料采用Tc4钛合金,材料性能见表2,其外径D2=118 mm、内径d2=90 mm,极惯性矩I1=1.259 3×107m4。向心关节轴承材料与偏心环一样,其内外径分别为Φ50 mm、Φ90 mm,宽度为36 mm,故可知单元矩形的长为36 mm,宽为20 mm,厚度取1 mm。

表1 合金结构钢 35CrMoV材料性能

表2 Tc4钛合金材料性能

3.2 向心关节轴承应力应变结构分析

将材料数据代入到式(10)中可求得:

将式(10)代入到式(7)中可得单元里任意一点x、y的应变函数。单元节点1、2点坐标分别为(-10,-18),(-10,18)。

将式(10)代入到式(8)中可得单元里任意一点x、y的应力函数。单元节点1、2点坐标分别为(-10,-18),(-10,18)。

即可知单元1、2所受到的应力均小于860 MPa,其应变均在0.1 mm左右,在材料承受范围之内。

3.3 导向装置模态分析

将参数代入公式(5),在偏心距保持5 mm不变,导向轴刚度保持不变,改变外壳刚度,使外壳刚度与导向轴刚度成一定比值的情况下,得到偏置力F随偏心装置距离调心轴承L1变化而变化的图像,如图5所示。

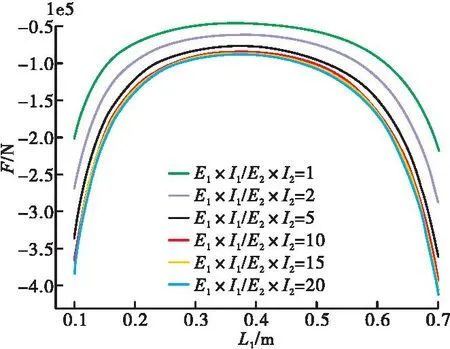
图5 偏置力随偏心装置位置变化

由图5可以看出,随着偏心装置向调心组合轴承靠近,偏置力大小总体上呈先上升后下降的趋势,且在接近悬臂轴承和调心轴承处变化趋势非常大,而在L1取[0.3,0.5]段时偏置力变化相对比较稳定,当外壳刚度与导向轴刚度之比到达5时,之后增加刚度比对偏置力大小的影响很小,故偏置力偏心装置设计在悬臂轴承与调心轴承中间较为合理。

将公式(5)中的F值取图5中外壳刚度与导向轴刚度之比为5时的最大值73 kN。改变偏心装置距离调心轴承L1,在不同的外壳刚度与导向轴刚度之比的情况下偏心距的变化情况如图6所示。

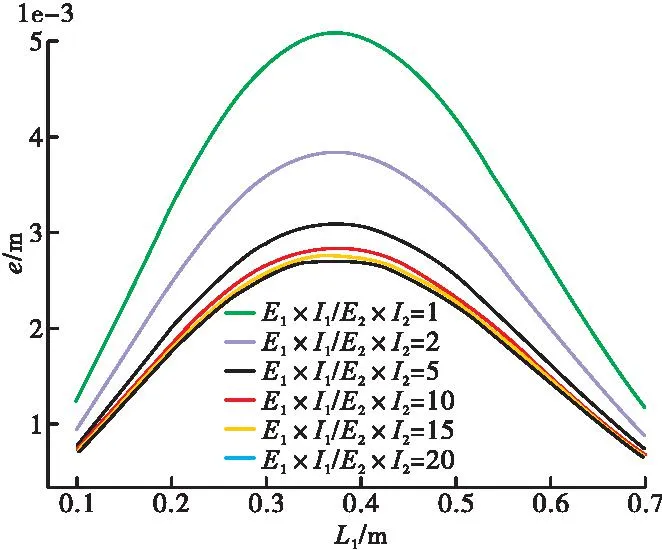
图6 偏心距随偏心装置位置变化

由图6可得,在取最大值F的情况下,偏心距会随着偏心装置安装的位置先增加后减小,当外壳刚度和主轴刚度比值达到5后,外壳刚度与导向轴刚度之比对偏心距的影响很小。

将不同的参数代入公式(4),同样在不同外壳刚度与导向轴刚度之比的情况下改变偏心装置距离调心轴承L1,得到钻头转角θ的变化图,如图7所示。

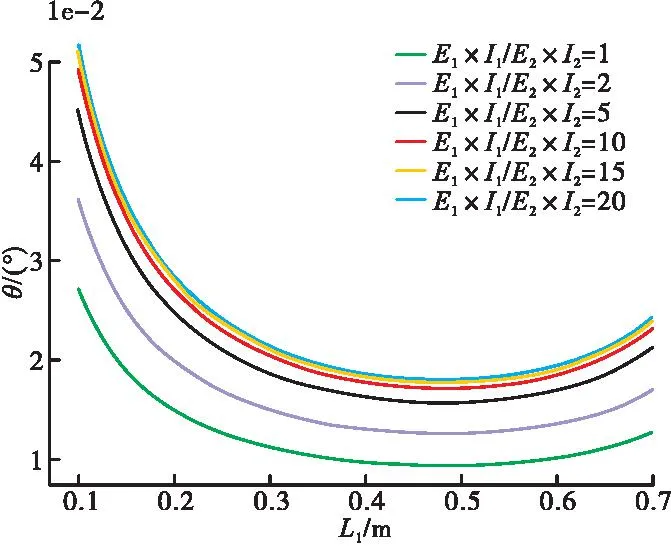
图7 钻头偏角随偏心装置位置变化

由图7可看出,随着偏心装置距离调心轴承L1越来越大,钻头转角总体呈下降趋势,且在悬臂轴承、调心轴承处钻头倾角变化趋势较为显著,同时外壳刚度与导向轴刚度之比大于5后,外壳刚度与导向轴刚度之比对钻头转角的影响比较小。

当L1越小,即偏心装置越靠近调心轴承时,钻头转角呈倍数增长,工具的造斜能力越强。如图5中,当L1取[0.3,0.5]段时,偏置力大小变化趋势非常小,所以在不影响偏置力大小的情况下,取L1等于0.3时,钻头转角较大,造斜能力较强。

对前后关节进行瞬态动力学分析,给定旋转约束,前关节受到钻压的反作用力,给定前后关节的边界条件,利用有限元软件进行数值模拟计算,得到前后关节在导向钻井工具中应用时的等效应力图和等效弹性应变,如图8、图9所示。

图8 前后关节等效应力

图9 前后关节等效弹性应变

前后关节采用合金结构钢 35CrMoV材料,通过球形万向节和前后关节传递动力,考虑钻压为50 kN的载荷,通过划分网格并进行运算。得到最大等效应力181.64 MPa,远小于屈服极限应力930 MPa,其薄弱点弹性应变最大只有0.001,满足设计要求。

4 结 论

1)通过纵横弯曲法建立力学模型,综合考虑指向式导向工具外壳和导向轴的相互作用,对导向轴及偏心环的向心关节轴承进行力学分析,推导出导向轴各单元的挠度、转角计算公式。

2)分析偏置力、偏心距和钻头转角随着偏心装置安装的位置及外壳与导向轴刚度比之间的关系,通过偏置力、偏心距、钻头转角的变化图,选择外壳刚度和主轴刚度之比为5,L1为0.3 m,偏心距为3 mm的设计参数。

3)通过有限元法建立等效力学模型,分析向心关节轴承及前后关节的应力应变分析,通过校核各参数满足材料的极限屈服强度。