基于径向基函数神经网络的永磁同步电机转速自适应控制策略∗

刘泓杉，刘慧博

(内蒙古科技大学信息工程学院，内蒙 古包头 014010)

PMSM 因其体积小、结构简单、可靠性高、良好的转矩和速度控制特性[1]等特点，使得在发电系统、医疗器械、机器人、电动汽车等领域中得到了广泛的应用。在这些应用中，具有良好的转速控制性能是极为重要的。在PMSM 的转速控制系统中，转子磁场定向控制(Field-Oriented Control，FOC)理论得到了广泛应用。然而，由于PMSM 是批量化产品，同一批次产品会也会存在生产不一致。同时，随着时间的推移，PMSM 也会因机械磨损、温度变化以及复杂的工作条件[2]等因素，导致电机的转动惯量(J)、阻尼系数(B)等参数存在不确定。此外，由于非线性摩擦和复杂的工作条件[3－4]，导致外界负载产生波动。参数的不确定性和复杂的负荷波动均会导致系统稳定性差，速度波动大。

近年来，PMSM 调速控制器的设计成为当前的研究热点，并提出了大量先进的控制方法来解决上述问题，以实现良好的调速性能。为了获得快速的动态响应和较强的抗波动性能，文献[5]提出了一种新的自抗扰控制算法，通过自抗扰控制可以实现转速控制的快速性和稳定性，但由于自抗扰控制算法的可调参数较多，控制效果高度依赖于参数整定，因此，难以应用于实际工程。文献[6]中，提出了一种优化的自抗扰控制算法，该方法基于一种新的非线性函数，构造了自抗扰控制器的各个分量，实现了转速控制的快速跟踪和较强的抗干扰性能。文献[7]提出了一种基于李雅普诺夫的新型控制方法，解决了PMSM 电机在复杂负荷波动下的转速控制稳定性。然而，在文献[3－5]中，均将J和B视为常数，没有考虑其结构参数的不确定性。在实际工程中，参数的不确定性往往会导致较差的速度控制性能，为此，文献[8]引入了一种带扰动力矩观测器(Disturbance Torque Observer，DTO)的自适应滑模控制方法来实现速度控制，该方法收敛速度快，且跟踪精度高。

文献[9]中，研究了一种结合非线性分数阶PID切换流形、扩展状态观测器和超扭曲趋近律的SMC方法，以实现较小的稳态误差。文献[10]中，引入了一种关于反步控制器(Backstepping Controller，BSPC)和干扰观测器(Disturbance Observer，DOB)结合的速度控制方案，该方法利用非线性DOB 来估计不确定参数和复杂负载转矩，经试验表明，该控制方案可以抵抗外界不确定性干扰，实现速度的稳定控制。文献[11]中，研究了一种结合积分项和SMC 方法的BSPC调速方法，以降低参数不确定性和负载波动的影响。文献[12]针对PMSM 设计了输出反馈非线性H∞控制器，具有较强的鲁棒性和抗波动性能。文献[13]通过引入带有补偿控制项的模型参考自适应控制(Model Reference Adaptive Control，MRAC)方法，实现了PMSM 电机转速响应的快速性和鲁棒性。在文献[8－12]中，同时考虑了复杂的负载波动和J、B的不确定性，提高了速度控制性能。然而，有许多控制器参数具有不确定性，往往通过反复试验来调整这些参数，高度依赖于控制参数的整定结果，此外，通过试错法获得的控制器参数通常是常数，并非对所有工作转速条件都是最优的。

文献[14]中，针对PMSM 提出了一种带有神经网络的速度控制方法，利用神经网络辨识不确定负载，实现了自适应控制。文献[15]中，提出了一种自适应神经有限时间跟踪控制方案，以获得精确的跟踪。在该方法中，一个神经网络用于估计参数不确定的函数，另一个神经网络用于观察不可用状态。文献[16]在神经网络的基础上，研究了一种新型的PMSM 速度控制算法，以获得对不确定参数和波动负载的良好自适应性能。考虑到参数不确定性和负载波动，文献[17]研究了一种基于递归小波的智能最优Elman NN 速度控制方案，以获得快速响应和良好的抗波动性能，在该方法中，最优控制律的逼近是通过神经网络实现的。在文献[13－16]中，均基于神经网络进行PMSM 转速控制，提高了永磁同步电机的速度控制性能，对后续的研究具有重要的指导意义。在各种神经网络中，径向基函数神经网络(Radial Basis Function Neural Network，RBFNN)具有网络结构简单、逼近性好、学习速度快、泛化能力强等固有特点，近年来被广泛应用于不确定和复杂的工业控制系统[17－20]。

然而，对于PMSM 的转速控制研究而言，利用RBF 神经网络进行优化控制，同时考虑复杂负载波动和不确定J、B的研究很少，在该方法的启发下，本文提出了基于RBFNN 的控制参数自适应整定方法。

本文针对PMSM 的转速控制问题，提出了一种结合自适应速度控制器和RBFNN 的转速控制解决方案，以减少参数不确定性和复杂负载波动的影响。与以往的研究结果相比，本文的主要贡献总结如下:①首先基于李雅普诺夫稳定性理论和考虑参数不确定性和负荷波动的电机转动方程，设计了一种自适应速度控制算法来实现速度控制，并证明了所提出的自适应速度控制算法是渐近稳定的，同时，自适应速度控制算法具有减小复杂负载波动和J、B不确定性对速度控制性能影响的特点。②鉴于自适应控制参数设计较为困难，考虑到复杂负载、永磁同步电机参数和自适应速度控制器(Adaptive Speed Controller，ASC)参数的不确定性，采用RBFNN 对ASC的所有参数进行优化，从而保证PMSM 电机在整个速度范围内均能获得最佳的速度控制性能。

本文在第1 节，考虑了PMSM 的参数不确定性和复杂的负载波动，并建立了PMSM 的数学模型。并以此为基础上，设计了渐近稳定的ASC 控制算法，并证明了控制算法的稳定性。第2 节，基于RBFNN 理论实现了速度最优控制。第4 节进行了试验验证与结果分析。

1 考虑参数不确定性和负载波动的PMSM 模型

为简化分析，假定PMSM:①不考虑磁路饱和。②不考虑磁滞和涡流损耗。③忽略作用在转子上的绕组阻尼。④磁场是正弦分布的。

此外，由于生产不一致、机械磨损、温度变化和复杂的工作条件等因素，导致J和B是不确定的。由于非线性摩擦和复杂的工作条件，负载是波动的。

根据FOC 理论和上述假设，PMSM 相对于d－q坐标系的电压方程和电磁转矩方程表示为:

式中:ud、id、Ld分别是定子在d轴的电压、电流、电感；uq、iq、Lq分别是定子在q轴的电压、电流、电感；Rs、ψf、ωe、Te、np分别是定子电阻、永磁体磁链、角速度、电磁转矩和极对数。

同时，建立了考虑参数不确定性和复杂负载波动的PMSM 动力学方程:

基于FOC 理论[5]，PMSM 的速度控制通常采用双闭环控制结构，由扭矩环(扭矩环通过两个电流闭环实现)和一个速度外环实现内转矩环，如图1所示。

图1 基于FOC 理论的PMSM 转速闭环控制

在本文研究中，重点关注PMSM 的转速外环控制，为了更加清晰地设计转速控制，结合式(3)可以将图1 进一步简化成图2 所示。

内部扭矩控制环相当于外部速度环的延时环节，扭矩闭环控制响应通常为微秒级，而PMSM 的时间常数为J/B，通常在毫秒级，因此，PMSM 的时间常数远大于扭矩的时间延迟。根据主导极点法，内部扭矩环的时间延迟可以忽略不计，因此，图2 进一步简化成图3 所示。

图3 PMSM 转速闭环控制框图

2 转速闭环控制设计

速度控制偏差e以及偏差的导数定义为如下:

如果电机的温度、磨损、生成一致性、外界负载均不发生变化，那么均为常数，为了分析这些因素对速度控制性能的影响，本文认为分别是J，B，TL的函数，而不是时间的函数。

本文选择的李雅普诺夫函数，如下所示:

式中:V是正定函数，k2是大于0 的有界增益，且:

将V求导可以得到:

将式(3)、式(5)代入式(8)可以得到:

考虑到速度控制的稳定性和偏差e的收敛性，必须是负半定，因此，ASC 转速控制律如下:

式中:k1>0 是有界控制增益。

将式(10)代入式(9)可以得到:

因此，ASC 控制系统是稳定的，且自适应＾J，

此外，根据(6)、式(11)可知，V是一个递减函数且有界，如下所示:

联立式(3)、式(5)、式(10)可得到:

根据式(11)可以进一步求导得到:

根据Barbalat 引理，可知:

根据式(11)、式(15)可以进一步得到:

表明，即使在J、B不确定且存在负荷波动的情况下，由ASC 控制仍然是渐近稳定的。

3 基于RBFNN 的转速控制参数优化

在第2 节详细分析了转速控制算法的理论推导并证明了控制律的稳定性，然而控制参数的取值决定了控制系统的动态响应性能，如超调量、响应时间等，在第3 节将系统阐述参数设计方法。

根据式(5)、式(7)、式(10)可以进一步将控制律写成如下表达式:

根据式(17)，可以看出控制律由反馈控制和补偿控制组成，其中补偿控制部分只需根据PMSM 转速及其转速的导数即可确定，反馈控制部分主要根据偏差e、偏差的导数以及偏差的积分线性组合得到，且控制参数k1、k2的取值将影响PMSM转速控制的动态响应性能，因此，如何优化反馈控制参数k1、k2的取值是极为重要的。

从反馈控制部分可以看出，反馈控制实际上是PID 控制算法的标准表达形式，因此，本文进一步将图3 的控制框图画成图4 所示。

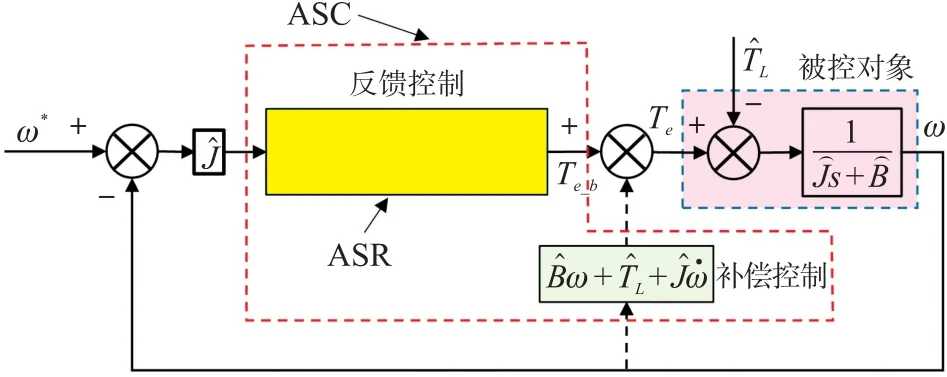
图4 基于反馈＋补偿控制框图

图5 基于RBFNN 的反馈控制参数优化原理框图

在各种神经网络中，RBFNN 具有网络结构简单、逼近性好、学习速度快、泛化能力强等固有特点，能够根据控制偏差，自适应调整控制参数实现最优控制，因此，本文提出基于RBFNN 的ASC 控制系统反馈控制部分的参数优化方法，其优化原理框图如下所示，其中RBFNN 的作用是根据反馈控制的输出u和被控系统输出ω进行系统辨识获取被控对象等效模型，然后根据辨识结果动态调整反馈控制参数k1、k2，实现期望转速的准确跟踪。

RBFNN 是一种局部逼近网络，可以逼近任意连续函数，是由Moody 等提出的一种具有单隐藏层的三层前馈神经网络模型，它模拟了人脑中局部调整和相互覆盖接收域的神经网络结构。

①网络结构:RBFNN 由输入到输出是完全非线性的，而隐藏层到输出层是线性的，可以加快学习速度并防止陷入局部最优，其网络结构如图6 所示。本文在RBFNN 设计中，设定总层数为3 层，输入层为3 个神经元，隐藏层为6 个神经元，输出层为2 个神经元。

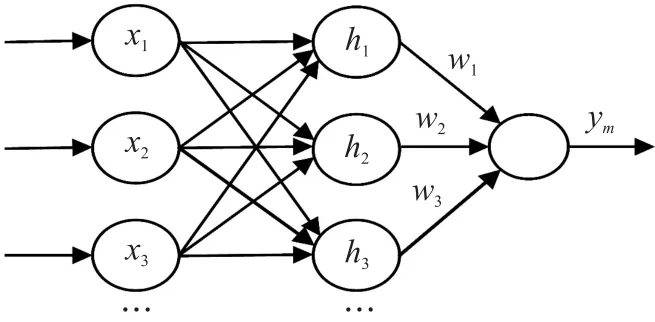
图6 RBFNN 网络结构

②被控对象Jacobian 辨识原理:在RBFNN 中，x＝[x1，x2，x3，…，xn]为输入变量，在本文中:n＝3，x＝[Te＿b，ω，ωlast]，其中，ωlast代表上一时刻的电机转速，设置径向基向量h＝[h1，h2，h3，…，hn]，其中hj代表高斯径向基函数:

网络的第j个节点的中心矢量矩阵Cj＝[Cj1，Cj2，…，Cji，…，hjn]，i＝1，2，…，n，假设网络的基宽向量为:

bj为基宽参数，网络的权向量为:

辨识网络的输出为:

辨识网络的性能目标函数为:

本文中，y(k)代表在k时刻的电机转速，ym(k)代表在k时刻的辨识系统的电机转速。根据梯度下降原理，输出权、节点中心及其节点基函数的迭代算法如下:

上面式子中，η代表学习率，本文取0.1，α代表动量因子，本文取0.01，Jacobian 阵算法为:

式中:取x1＝u(k)，k1、k2的调整采用梯度下降法，如下所示:

4 仿真实验验证与分析

为了验证本文提出的基于RBFNN 的ASC 控制算法的有效性，选取了某一典型PMSM 电机作为研究对象，并在MATLAB/simulink 环境下搭建了电机模型以及基于RBFNN 的ASC 控制算法，本文所选电机的基本参数如表1 所示。

表1 PMSM 参数

搭建的仿真模型如图7 所示。

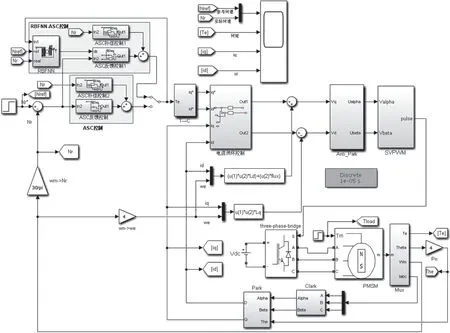
图7 基于RBFNN 的ASC 控制仿真模型

在仿真模型中，PWM 开关频率为10 kHz，仿真步长0.000 01 s，ASC 反馈控制中的控制参数k1初始值为0.1，k2初始值为1；RBFNN 中，采用3－6－2网络结构，其学习速率设置为0.1，动量因子α＝0.01，隐含层的节点数量为6。

5.1 转速控制验证

为了观察PMSM 电机在整个转速范围内的动态响应性能，选择100 rad/s(低速)、200 rad/s(中等转速)和300 rad/s(高转速)作为参考转速，施加固定负载转矩5 N•m，并且对测量的转速施加高斯白噪声，模拟真实电机转速测量值，分别对比ASC 控制算法和基于RBFNN 的ASC 算法的转速动态控制效果，3 种不同转速下的控制效果如图8(a)、图8(b)、图8(c)所示。

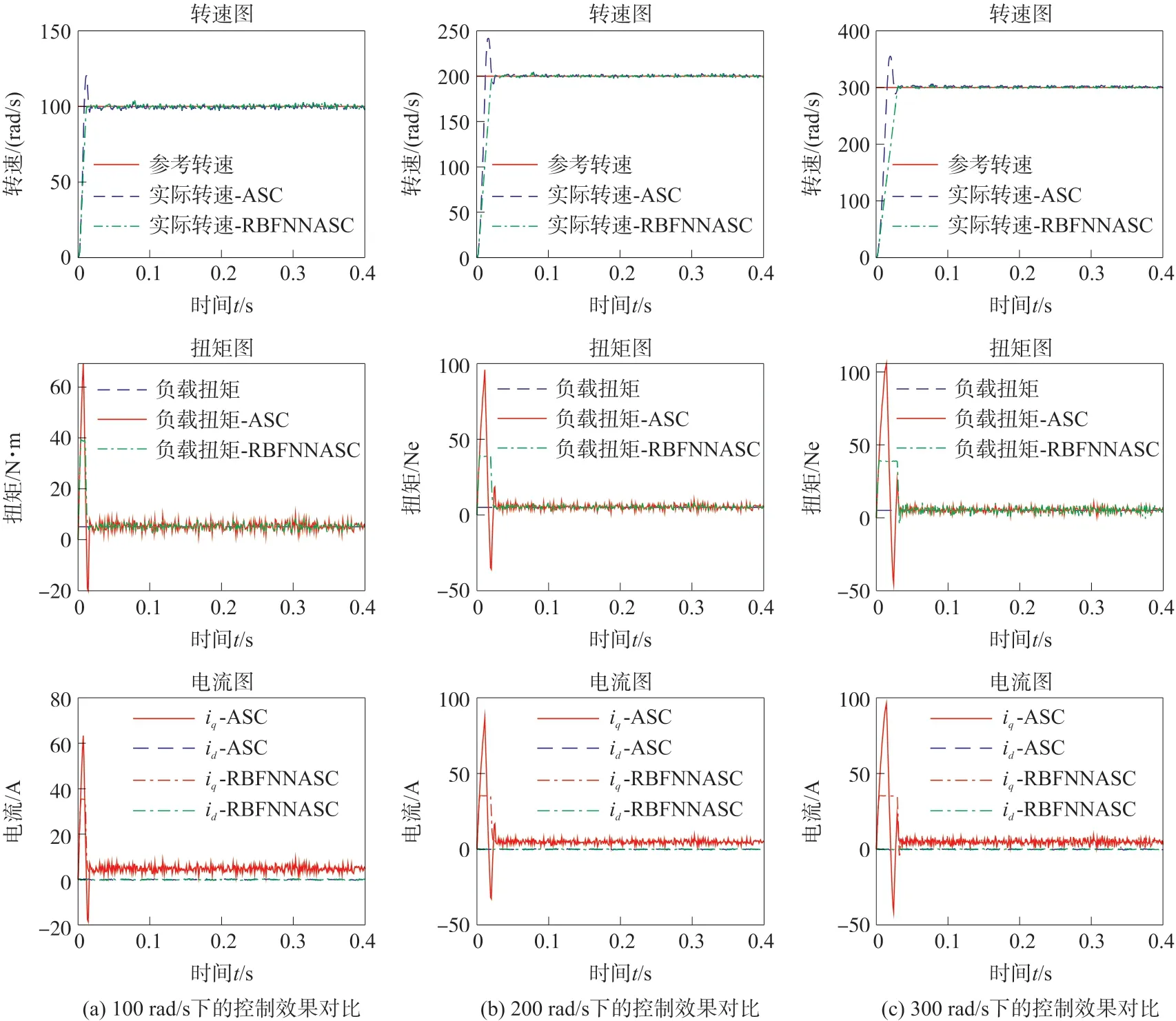
图8 ASC 与RBFNNASC 算法在不同转速下的控制效果对比—(固定负载)

图8(a)显示了阶跃参考速度为100 rad/s 时的响应曲线。在初始时刻，参考转速从0 变为100 rad/s。①ASC 与RBFNNASC 两种方法都能快速达到期望转速，转速响应时间大概是0.02 s(响应时间按照达到控制目标的90%的时间计算)，然而ASC 算法存在一定的超调，RBFNNASC 则快速平稳地达到了目标转速。②电机扭矩最终与负载扭矩趋于一致，稳定在5 N•m 附近。ASC 算法的输出扭矩最大值为69 N•m，且波动较大，而RBFNNASC 算法则最大扭矩为39 N•m，并且在初始阶段，扭矩没有出现扭矩正负交替的情况。③在ASC 控制下，iq的波动约为(5±3.2)A，在RBFNNASC 控制下，iq的波动约为(5±3.4)A。虽然RBFNNASC 的iq波动略大于ASC 控制，但在实际应用中5±3.4 A 是可以接受的。

图8(b)显示了阶跃参考速度为200 rad/s 时的响应曲线。在初始时刻，参考转速从0 变为200 rad/s。①ASC 与RBFNNASC 两种方法均快速达到期望转速，ASC 的转速响应时间大概是0.02 s，但ASC 算法超调量较大，而RBFNNASC 转速响应时间大概是0.03 s，虽然响应时间稍晚有所增加，但其能够快速平稳地达到目标转速，并且没有超调。②在动态调节阶段，ASC 算法的输出扭矩最大值高达93 N•m，且波动较大，而RBFNNASC 算法则最大值仅为42 N•m。③在ASC 控制下，iq的波动约为5±2.5 A，在RBFNNASC 控制下，iq的波动约为(5±2.6) A。RBFNNASC 的iq波动略大于ASC 控制。

图8(c)显示了阶跃参考速度为300 rad/s 时的响应曲线。①300 rad/s 的目标转速下，ASC 与RBFNNASC 方法均快速达到期望转速，ASC 响应时间为0.025 s，ASC 算法超调量较大，而RBFNNASC响应时间大概是0.032 s，虽然响应时间稍晚有所增加，但超调极小。②在初始阶段，ASC 算法的输出扭矩最大值高达106 N•m，RBFNNASC 算法则最大值仅为40 N•m。③在ASC 控制下，iq的波动约为(5±3.6)A，在RBFNNASC 控制下，iq的波动约为(5±3.8)A。

5.2 负载动态变化下的转速控制验证

为了验证ASC 算法与RBFASC 算法在整个转速范围内的抗扰动性能，分别设定电机在100 rad/s(低速)、200 rad/s(中等转速)和300 rad/s(高转速)作为参考转速，然后在0.5 s 处，负载扭矩突然由5 N•m 变为30 N•m，在0.7 s 时，负载扭矩从30 N•m 再次变为5 N•m，ASC 与RBFNNASC 算法在不同转速下的控制效果如图9(a)、图9(b)、图9(c)所示。

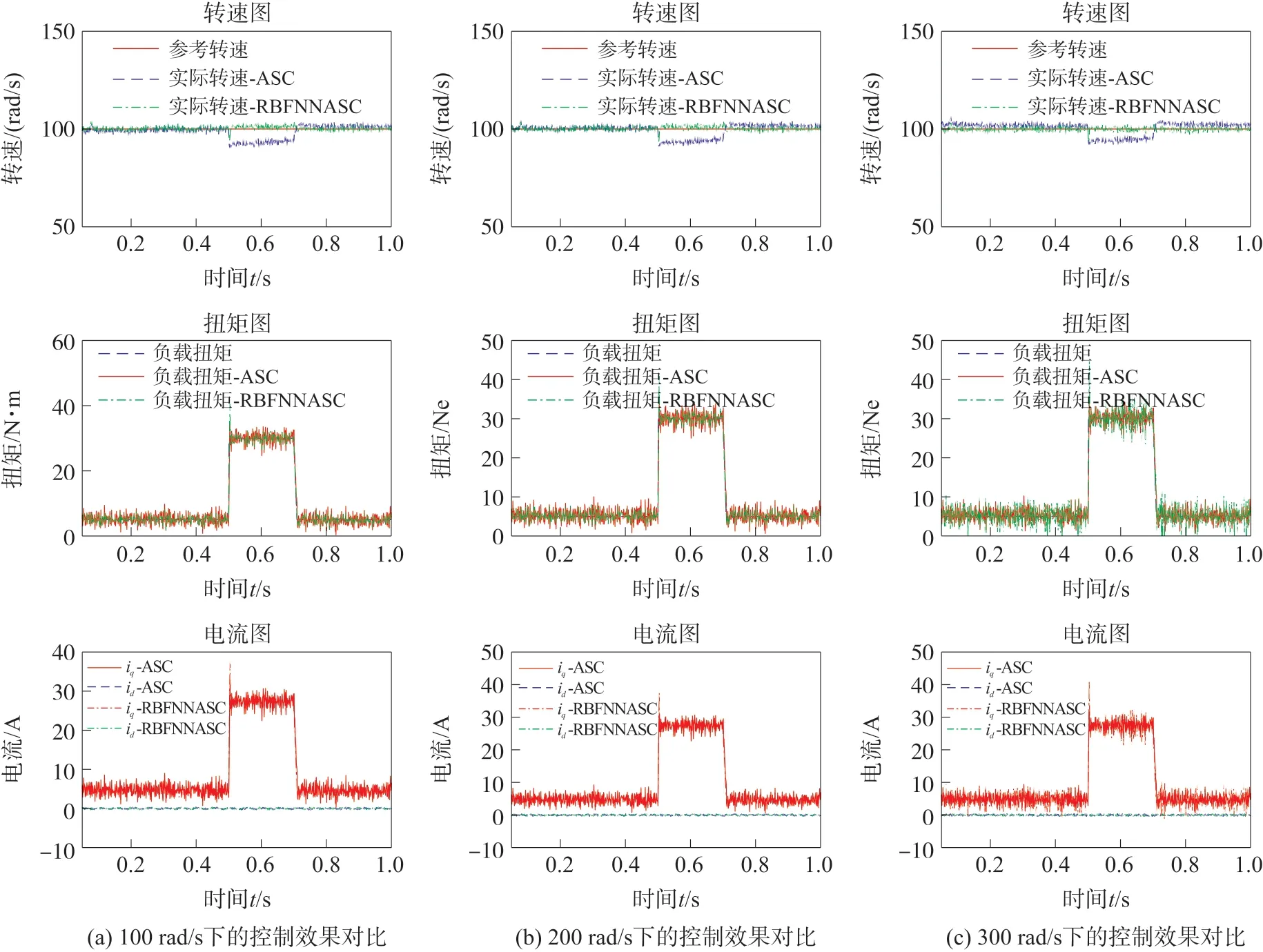
图9 ASC 与RBFNNASC 算法在不同转速下的控制效果对比二(负载动态变化)

从图9(a)可以看出:100 rad/s 的目标转速下，0.5 s 处，负载扭矩突然变为30 N•m 后，ASC 算法的转速急剧下降至89 rad/s，维持0.2 s 后，负载扭矩突然变为5 N•m，其转速再次恢复至100 rad/s，在负载突变时，其转速发生了较大变化。然而，RBFNNASC 算法则在0.5 s 处，负载扭矩突变时刻，快速增加输出扭矩使其维持在目标转速100 rad/s附近，在0.5 s～ 0.7 s 之间，其稳定转速大约在102.5 rad/s，略高于目标转速。

从图9(b)可以看出:200 rad/s 的目标转速下，0.5 s 处，负载扭矩突然变为30 N•m 后，ASC 算法的转速急剧下降至191 rad/s，维持0.2 s 后，负载扭矩突然变为5 N•m，其转速再次恢复至200 rad/s，在负载突变时，其实际转速相对于目标转速下降了9 rad/s。然而，RBFNNASC 算法则在0.5 s 处，负载扭矩突变时刻，也能维持在目标转速200 rad/s 附近，在0.5 s～0.7 s 之间，其稳定转速约为202 rad/s，略高于目标转速，实际转速相对于目标转速变化量为2 rad/s。

从图9(c)可以看出:300 rad/s 的目标转速下，0.5 s 处，负载扭矩突变后，ASC 算法的转速急剧下降至291 rad/s，维持0.2 s 后，转速再次恢复至200 rad/s，在负载突变时，其实际转速相对于目标转速下降了9 rad/s。RBFNNASC 算法则在负载扭矩突变时，能维持在目标转速200 rad/s 附近，在0.5 s～0.7 s 之间，其稳定转速约为200 rad/s，实际转速与目标转速非常接近。

通过图9(a)，图9(b)，图9(c)可以看出，相对于ASC 算法而言，RBFNNASC 算法的转速波动显著下降，其抗干扰能力显著提高。

因此，RBFNNASC 在整个速度范围内具有良好的系统稳定性、快速的响应性和较强的抗波动性能。

6 结论

针对J、B的不确定性以及外界负载波动导致系统稳定性差，速度波动大的问题，本文提出了一种基于RBFNN 的ASC 控制方法。首先，考虑到PMSM 的参数不确定性和复杂的负载波动，建立了永磁同步电机的动态运动方程。其次，构造了正定的Lyapunov 函数V，并通过构造一个负半定的，保证了ASC 是渐进稳定的。然后，将ASC 算法控制律分解成补偿控制和反馈控制部分，通过分析可以知道，补偿控制部分只需根据PMSM 转速及其转速的导数即可确定，然而反馈控制部分的控制参数k1、k2的取值将影响PMSM 转速控制的动态响应性能。接着，本文提出基于RBFNN 的ASC 控制系统反馈控制部分的参数优化方法，RBFNN 根据反馈控制的输出和被控系统输出进行系统辨识获取被控对象等效模型，然后根据辨识结果动态调整反馈控制参数k1、k2，实现期望转速的准确跟踪。最后，通过不同转速下，ASC 算法与RBFASC 算法的控制效果对比表明，RBFNNASC 速度控制方法在整个速度范围内具有良好系统稳定性、快速的速度响应和较强的抗波动性能。