“视点”与世界几何秩序的构建——托勒密《地理学》制图思想新探

鲁博林

(清华大学 科学史系,北京 100084)

托勒密(Claudius Ptolemy,约公元100—170年)的《地理学》(GeographicalHyphegesis)作为古代西方地学和制图学方面的代表著作,自文艺复兴以来一度主导西方世界图像和地理观念的塑造。遗憾的是,自近代科学革命以来很长一段时间内,科学史界对该书并未投以特别的关注——在许多史家眼中,它或被视为一部无关思想的制图手册,或被认为是过时的古代地理论述。直到19世纪,西方古典学界逐渐认识到《地理学》的历史价值,以诺布(C.F.A.Nobbe,1791—1878)等学者为首开始对庞杂的《地理学》抄本谱系进行校勘、编定,继之有昆茨(O.Cuntz)、费舍尔(J.Fischer)等奠定了该书文献研究的基础。以此为前提,《地理学》在20世纪之后逐渐进入科学史的视野,但受限于“分科治史”的实证史进路影响,托勒密的制图方法始终被诺伊格鲍尔(O. Neugebauer)等史家视为现代投影的古代雏形,因而成为一种合理但过时的地图投影尝试。[1-2]而埃杰顿(S.Y.Edgerton)等艺术史家则努力在《地理学》与近代透视法之间建立联系,以图证明这部古代作品所潜藏的现代性。[3]两者看似殊途,实则反映的都是基于现代科学视角的治史进路。地图史家迪尔克(O.Dilke)更是在哈利(J.B.Harley)与伍德沃德(D.Woodward)编定的《制图学史》中,以典型的辉格史语调对该进路下的托勒密《地理学》做了盖棺论定的评价。[4](1)在迪尔克看来,托勒密《地理学》的核心是其“地图投影理论”,而投影理论的贡献在于“对后世制图学发展的重要性”。这种典型的辉格史论调颇能代表20世纪科学史界对《地理学》的普遍态度。另外由于该书在中世纪长期沉寂,至文艺复兴后才有广泛影响,所以相关研究也侧重后者的时段,对其古代起源的研究并不受到重视。

然而近几十年来,随着科学史界的思想史转向以及该书新译本的相继出版,国际学界开始进行新一轮评注和解读。(2)该书最新的英译本为伯格伦与琼斯对理论章节的节译本(Berggren &Jones, 2000);而德译本则为伯尔尼大学“托勒密研究中心”(Ptolemaios-Forschungsstelle)历经十年的编译成果,并附古希腊文对照Stückelberger &Graßhoff(2006)。其余英译大多为早期史蒂文森(E.L.Stevenson)令人不甚满意的拉丁文英译本的重印。以陶布(Liba Taub)、琼斯(A.Jones)等为代表,科学史家开始从思想史、哲学史的角度重估托勒密的诸多作品。[5-6]《地理学》自然在重估的作品之列,如费凯(Jaqueline Feke)、谢格罗夫(D.Shcheglov)等学者便基于对关键性概念在同时代著作中的运用所做的语言学分析,试图阐明古希腊地学、斯多亚哲学和托勒密的数学哲学对该书的影响。[7-8]然而,类似讨论仍基于概念界定等理论文字展开,对制图步骤的细节着墨不多。确切地说,当下学界对托勒密地理制图的数学理解,仍基于20世纪70年代诺伊格鲍尔等人的解读。这在很大程度上,妨碍了科学史学者对作为古代数学化作品的《地理学》数学思想的深入分析。更不必提,由光学角度或视点切入托勒密制图的研究几乎仍处于空白。因此在下文中,我们将首先点明《地理学》作为数学化作品的本质特征,以此将其置于古希腊地理传统中并引出“视点构建”的重要性。以假想的“视点”为线索,本文试图借助对托勒密制图过程的重构,揭示视点背后的光学与几何思想,并展示《地理学》如何在此基础上综合古代的数学传统,将居住世界纳入一个宏大的古代数学世界图景之中。

1 《地理学》观念概说与制图新论

《地理学》的希腊语原题为Γεωγραφικφγησις(英语:Geographical Hyphegesis),意为“地理描绘指南”,学界一般简称为“地理学”。在古代西方的地学语境中,“地理”(γεωγραφα)是一个涵盖范围相当广泛的概念,既可以指对不同地域民族地貌的文学类记载,也可以指对已知世界轮廓的图像化描绘。但自从希腊化时期的亚历山大学者埃拉托色尼(Eratosthenes)第一次在传世文献中明确以“地理”为题撰写专著以来,制图尤其是基于天文几何方法的数学制图,便成为了古代地理学的应有之义。[9]同属亚历山大学派的托勒密《地理学》,正是在这一意义上展开论述的。不仅如此,托勒密还将“地理”的内涵精准地规定为“世界制图”,使之不仅和现代地理概念大相径庭,也和当时与地理描绘相关的其他概念区别开来。故而甫一开篇,他便如此写道:

地理学是一种模仿,是对整个世界的已知部分和与之关联的事物的绘制。它与地志学(χωρογρφα, chorography)不同,后者作为独立的门类,着手描绘相互独立的地区,并切实记录下尽可能多的各项事物;而地理学的本质是把已知世界作为一个单一的、连续的实体来展示,展示其性质和排布方式,它只关注与边界、轮廓相关的元素。(PtolemyGeography1.1.1-2)([10],57页;[11],52-53页;[12],3页)(3)本文参考的《地理学》译文综合了最新的英译和德译本,对关键概念的阐释则核对了由诺布(Nobbe)编定的古希腊文本。此处英译本将“地理学”译为“世界制图学”(world cartography),“地志学”译为“区域制图学”(regional cartography),意在加以普及性的阐释,本文基于思想史研究的立场,主张仍译为“地理学”和“地志学”,以还原其知识语境。此段重点参考了德译本和诺布本。

这里托勒密将“地理学”(geography)和“地志学”(chorography)相对举,前者指的是对整个世界的地理描绘,而后者是对部分区域的地理描绘,此处的描绘主要就图像而言。因此他将地理学比喻为“画一幅完整的头部肖像”,而地志学则类似“只有耳朵或眼睛的图像”。与后者相比,地理学更重“量”而非“质”,强调距离的合比例大于摹仿的逼真。因此数学方法在地理学中“占据着绝对的优先性”,其目标就是“尽可能按照真实世界的比例来绘制地图”。(Geography1.1.5-7)可见书中所谓“地理学”,本质是对已知世界大致轮廓的几何绘制。

然而须注意的是,这里的“世界”并非现代意义上覆盖全球的地理范围,而是当时古希腊罗马文明已知的地域。在托勒密所继承的古代地学传统中,有一个专门的术语对此加以指代,即οκουμνη (oikoumene),意即“有人居住的世界”或“居住世界”。早在亚里士多德的《气象学》(Meteorologica)中,该词就作为希腊地理论述的核心被提出。亚氏选取了希腊语中表示居住的动词“οκω”,以该词的阴性现在时中动态分词形式搭配表示“大地”的词“γ”,组成了“οκουμνη γ”(有人居住的大地),再将其截取为缩短形式,便造出了οκουμνη一词。[13-14]在古希腊的知识语境中,“居住世界”的含义几乎等同于“已知大地”(包括周边海洋与岛屿)。古代西方的地理论述借此得以开辟出一方独立空间。尤其在地球观念成为共识后,居住世界相对于地球和天界的位置关系逐渐明确,如亚里士多德所言,“居住世界的宽度(纬度)是有限的,在一定的气候范围内,可延伸为围绕地球一条相续不断的环带”。[13-14]埃拉托色尼则进一步将其限定在赤道以北、极圈以南、东西跨度不超过半球、约占球面四分之一的象限之内。[15]

托勒密的地理写作,基本延续了传统的“居住世界”图景。兼之身处罗马帝国领土扩张与贸易交往空前繁荣的时代,作者对居住世界的尺度有了更切实的认知。他意识到要在平面上描绘横跨半个地球的居住世界,必然面临相似性与合比例性、便利与尺度精准的两难。《地理学》对此也毫不回避地加以讨论。他首先将地理制图分为“球面制图”和“平面制图”两大类型。前者是对大地形状的原比例缩小,不涉及任何形变,但难以制作和观看;后者更加一目了然,方便浏览,却须加以复杂的几何设计。(Geography1.18)对继承了古希腊地学传统的托勒密来说,如何设计出一种更好的平面制图法才是重点所在。但由于从球面到平面的转换必然存在形变,哪些比例应当保留,哪些比例只能舍弃,就成为必须加以选择的问题;同时,他还希望保持世界制图“在形状上同真实的居住世界尽可能相似”,这进一步规定了比例保留的限度与表现形式。([10],82页)基于上述考量,一定程度上定量化、几何化呈现的“合比例性”与“相似性”,成为了托勒密搭建地理制图框架的两大基本原则。[7]

从现代制图理念的角度加以反观,可知相似性与合比例性根本上是难以兼顾的。对相似的绝对追求很大程度将进入光学的论域,进而导向文艺复兴后兴起的透视理论;对合比例原则的恪守则可能根据比例的细分,如距离、角度、面积等的不同,被归入不同的现代投影类型。显然,托勒密的制图并非其中任意一种,而是力图在两者之间求取平衡。这自然使得《地理学》中的制图体系很难在数学内部实现完全自洽。但恰恰是在这种矛盾和复杂的张力中,托勒密给后人呈现了相当独特的几何设计。该设计的难点在于,如何将两种看似矛盾的原则统合为一体,并在相当程度上兼顾两者。从《地理学》构建的体系来看,托勒密是成功的,以至于地理史论述在提及托勒密制图法时,往往以“投影”等现代术语加以称呼。但事实上,无论是托勒密本人的论述,还是古代西方的制图传统中,都无“投影”一说。[16]这种辉格式表达在方便现代人理解的同时,实则妨碍了对托勒密制图的深入研究。近年来,研究者开始意识到这一问题,如英译者琼斯(A. Jones)认为,《地理学》的制图法由于数学上的不一致,更像是某种“定性模仿”(qualitative imitation)。([10],39页)不过仅仅以“定性”来盖棺论定托勒密的制图体系也不公平。应当说,为了将相互矛盾的原则加以统合,托勒密的设计有不甚严密甚至跳跃之处,但就制图框架的实用性和可扩展性而言,他的方法体系仍不失为数学上的杰作。最重要的是,托勒密在西方乃至世界地理制图史上,第一次依托视点的假定和转换,完成了对世界地图的系统性几何构建,由此呈现的世界图景也对西方的地理和制图思想产生了决定性影响。在下一节中,我们将以托勒密的第一和第二平面制图法为例,详细展示托勒密是如何基于想象的视点,创造性地搭建起他的地理制图体系的。

2 从“视点”出发:托勒密地理制图的数学重构

《地理学》中一共提到了3种平面制图方法,其中前2种专门用于地图制作,第3种则用于展示当时流行的地球环仪(ringed globe)上的居住世界图像(更接近于透视图像)。(4)这里的“地球环仪”托勒密称为“Κρικωτπης σφαρας”,即在常见的天文仪器环仪(即中国古代“浑仪”)中嵌入地球仪。该仪器外层共包含了7个代表天球大圆的环圈,分别为天球赤道、黄道、穿过分点的经线、南北回归线、北极圈和南极圈。根据托勒密的记载推测,这很可能是一种当时用于表现居住世界、地球和天球关系的展示型仪器(Geography 7.6.1)。因此我们重点讨论前2种方法。首先是托勒密的第一平面制图法。在引入具体的绘制步骤之前,作者从视觉成像原理的角度阐述了设计依据:“当视线开始投向球面北部象限的中央,即居住世界大部分所在的位置,此时让球体相对于眼睛转动起来,使得每根经线都相继位于眼睛的正对面、且经线平面穿过视锥顶点(κορυφςτςψεως),经线就会呈现为直线。然而纬线却不会如此,因为北极的位置偏离了视轴(ξονοςτνψεων),于是纬线明显呈现为向南凸出的圆弧状。”(Geography1.20.6)([10],82页;[11],110-111页)

命题22:如果一段圆弧被置于眼睛所在的平面内,那么圆弧将呈现为一条直线。(图1右)[17]

根据托勒密的规定,由于视点与球面相对地轴转动,每根经线会在不同时刻相继处于眼睛的正对面即视平面之内,因此原本作为圆弧的经线相对于视点自然呈现为直线。相比之下,纬线的再现依据似乎更加复杂。与之相关的首先是《光学》中的“命题10”:

命题10:当一个平面位于眼睛的下面,则平面上越远的地方,看起来越高。(图1左)[17]

图1 欧几里得《光学》命题10(左)与命题22(右)示意图[20]

该命题中,眼睛与平面的相对位置与托勒密所说的视点与纬线平面的位置是相符的。命题结尾还附加了一个推论:“在更高处看到的物体,看起来将是凹陷的。”[21]这就意味着,处在视点斜下方的每一条纬线,都会呈现为两头高、中间低的曲线。在古希腊的几何传统中,曲线或者是圆(弧),或者是圆与圆或直线的叠加。正如数学史家克莱因(M. Kline)所言:“希腊人不仅把数学主要限于几何,他们甚至把几何只限于那些能用直线和圆做出的图形。”[22]据此托勒密选择了最简化的形式,将所有纬线都设定为“向南凸出的圆弧”。进一步地,托勒密还将球面上经纬线的关键几何特征挪用于平面。比如,球面上的纬线都是相互平行,因此地图上的纬线圆弧也应相互平行,即互不相交的同心圆。再如,球面上的经线都(在北半球)相交于一点并与纬线垂直,因此地图上的经线也相交于一点并与纬线垂直,实际等同于纬线圆弧的半径,所交之点即共同圆心。

上述规定主要出于相似性的考量。要在平面上保留球面居住世界的大致比例,托勒密还需要对重要经线与纬线的长度比加以规定。一方面,由于地图上的纬线组成了一个同心圆框架,该框架中纬线长度变化与纬度变化成正比关系,这与球面上的余弦函数关系显然不符。(7)在托勒密制图法中,同心圆半径上的单位长度与单位纬度成正比,而纬线作为圆弧同样与半径长度成正比,因此纬线λ与纬度φ的变化亦称正比关系,即Δλ=αΔφ。但在球面上,纬线(圈)的长度λ与相应纬度φ的关系遵守余弦变换,设地球半径为r,则λ=2πr*cos(φ)。因而从数学上讲,托勒密只能保证两条纬线的长度与真实比例相符。为了控制居住世界的整体形变,他最终选择了最长和最短的两根纬线,即穿过极北之地图勒(Thule, 63°N)的纬线以及赤道。另一方面,由于所有经线都呈现为过共同圆心的直线,托勒密设计了一种独特的几何变换,即假定经线是从球面上“展平”在地图上的。故而经线上的1单位弧长(即1度)对应于1单位长度。这样,不仅地图上所有经线都等长,每一纬度对应的长度也相等,由此提供了合比例制图的基础。但相应的,单位经度与单位纬度对应的长度比(以下简称“经纬比”)却难以做到和球面处处相同。为此,托勒密延续了马里诺(Marinus of Tyre,活跃时间早于托勒密,但生卒年不详)的做法,仅保留了地学传统中作为世界中线的罗德岛(Rhodes, 36°N)的经纬比,即cos36°≈4∶5。(Geography1.21)经由上述对“纬线比”和“经纬比”的详细规定,第一制图法的定量数学框架便确定下来。最终呈现的图式十分类似于现代制图学的“圆锥投影”(如图2所示)。

图2 托勒密第一平面制图法几何框架示意图([23],1396页)

不过在上述图示中,可以明显看出第一制图法与圆锥投影的不同。图中以赤道为界,南北半球的图像出现了某种断裂。这是因为在赤道以南,纬线长度实际是递减而非递增,使得前述原则不再适用。因此在实际制图中,托勒密按照镜像对称的原理,直接按同纬度的北部纬线长度规定了南界纬线长度,再将相应经度的点与赤道直接相连,遂令南半球图像出现了严重扭曲。但即便在北半球部分,严格符合比例的仅有南北纬线之比、罗德岛的经纬比两对数量关系,([4],186-187页)因此无论就相似性还是合比例性而言,该地图都与球面的世界图像相距甚远。究其原因,则可追溯到托勒密一开始所设“视点”的局限。因此突破的关键便是对视点做出改进。基于上述思路,托勒密紧接着提出了他的第二平面制图法。将视点稍作调整,使得视轴同时穿过以下两点:(1)中央经线与中央纬线的交点;(2)地球的球心。(Geography1.24.10)([10],88页)同时令视点与球面保持一定距离,使得眼睛所见的差不多等于一个半球。对于这一点的几何推论,我们同样能在欧几里得《光学》中找到相关依据,即“命题23”和“命题24”。其表述如下:

命题23:单眼以任意方式看到的球体总是小于一个半球,而且所见球体本身呈弧形。

命题24:当眼睛靠近球体时,所见部分会进一步缩小,但看起来会变多。[17]

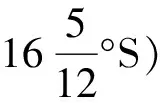
具体到绘制步骤,第二制图法遵循了与第一制图法相近的流程:首先根据视点位置确定呈现为直线的球面大圆,再加以展平。在第一制图法中,被展平的是先后位于中央的各经线;在第二制图法中,被展平的除了中央经线,还有过居住世界几何中心且与前者垂直的大圆。然后辅以平面几何推导,便能找到地图纬线圆弧的圆心位置。共同圆心一旦确定,各纬线的位置也相继确定。至此两种方法的步骤都是相近的。但第一制图法只须连接圆心与罗德岛纬线上按固定经纬比隔开的各点,便可得到作为直线的全部经线;而第二制图法则应在三条标准纬线上按照各自纬度相应的经纬比,计算出固定经度间隔(托勒密设定为5度)对应的线段长,以此标定不同经度的一组三点,方可依此绘制作为圆弧的经线。显然,第二制图法在制图流程上要更加繁琐,在后期根据经纬度标定地点时也不如第一制图法那样便利。但无论就相似性上还是合比例性而言,第二制图法都优于第一制图法,诚如托勒密自己所言,其“纬度范围和经度范围之比更加准确了”。 (Geography1.24.25)([10],93页)由此绘制出来的居住世界图像如图3所示。可以看出,不仅地图的整体轮廓更加符合球面呈现的外观,而且赤道以南部分也依照相同规则绘制,从而被纳入了统一的数学框架之中。([11],132-133页)

图3 托勒密第二平面制图法框架示意图([4],187页)

从第一制图法到第二制图法,视点的构建转换扮演了关键角色,同时也使古代制图在数学层面实现了质的飞跃,以至于在相当长时间内,许多制图史家都直接将其称为近代意义上的、基于特定几何点展开的“投影”(projection)。([23],883页;[10],36页)但正如前文所言,托勒密的时代既无“投影”概念,本文也反对专业研究者依附于这一出于权宜或普及之便而采用的说法。因“投影”本质是数学上的“点对点”映射,即所绘图形应当能通过将曲面上的点(L,φ)按照统一的函数f(L,φ)逐点、连续地投射到平面上的相应点(x,y)来直接获得。([23],879页)但显然,托勒密的制图法既非逐点映射,也不存在融贯一致的数学方法。事实上,《地理学》的制图至少综合了3种数学方法,其中包括:以欧几里得《光学》为代表的古希腊光学命题、传统的欧氏平面几何定理和托勒密自行设计的“展平”方法——为了求取相似性与合比例之间的平衡,三者在适用性和量化结果上并不一致。但借助假想的视点,托勒密巧妙地将三者统合为一体,构建出西方地图史上第一套系统性的几何制图理论。而潜藏在视点背后的,是有别于现代投影的制图思想和托勒密独特的数学世界图景。

3 “视点”的制图思想与数学世界图景

应当注意的是,光学和制图学的宗旨原本并不相同:欧氏光学的目的是“解释眼睛所见之物,而非模仿它”[26];而地理学却是“模仿”而非解释。换句话说,光学是将视觉现象还原为几何命题,制图学则旨在用几何命题重构现象。两者似乎构成了互逆的关系。但《地理学》的写作不只为还原视觉图像,也意在保留原有的数学比例,即在前述“相似性”与“合比例性”之间求取平衡——这也是托勒密制图与光学“嫡传”透视法的关键差异所在。因此,地理制图理论并非纯然是几何光学理论的“逆命题”,毋宁说,光学是再现居住世界所依托的数学传统之一——其中的关键便是“视点”。正是依托于特定视点,托勒密得以规定地图上经纬线的基本性质,并设计了展平的数学步骤。视点的不同将决定经纬线框架的不同以及展平对象的差异。在由此确立的“脚手架”基础上,构建制图体系的平面几何操作方才得以顺利展开。

视点在托勒密地理制图中的重要意义,也体现在数学家托勒密对古代制图思想的革新。地图绘制早在古典希腊时代便大量存在。在地球说兴起之前,古希腊人将居住世界视为一个巨大的平面,周围被大洋环绕,与此相应的地图则是圆形的周航图(γςπεριóδους)。[27-28]地球说兴起之后,亚里士多德、狄凯阿科斯、波西多尼奥斯等学者对居住世界的形状重新加以阐释,引出了长形、四边形、悬带状等多类地图,然而其共同点是制图过程均不存在视点,甚至是非数学的。[29]到了埃拉托色尼的《地理学》(Geographika)中,他将该学科确立为一门以描绘世界图像为宗旨、以几何学为主要方法的知识门类,居住世界的范围、位置,以及不同“地块”(σφραγδες)的大小和形状都可以计算得到。[30,9]遗憾的是,由于该书大部分已散佚,今人很难确定埃拉托色尼是否绘制过地图,但他却在传世长诗《赫尔墨斯》中,描绘了一种独特的地理视角:

赫尔墨斯从天界望去,

赫然看见五段美丽的“纬度带”:

“有两条的色彩,比幽然闪烁的蓝色更深;

一条呈红粉状,似是淬火而出……

还有两条环绕着两端的极点,天寒地冻。”[31]

此处作者借神祇之眼俯瞰地球,似乎预设了可用于制图的视点存在。只是诗性的想象并不等于数学的确立。事实上自埃拉托色尼以降,古希腊罗马的地图绘制在几何上有了长足进步,甚至发展出等间隔矩形地图、梯形地图等沿用后世的制图方式,但严格意义上的视点却并未真正出现。应当说,托勒密以前的世界地图绘制,更像是对小范围地图的简单扩大,很少考虑到世界尺度上球面的曲率和平面化的形变。正如斯特拉波所说:“我们的想象力能轻易地把平面图形转换到球面上去。”(Strabo 2.5.10)[32]但果真如此吗?与斯特拉波几乎同时代的托勒密,率先意识到其中的问题。在《地理学》中,托勒密严格指出了平面制图中形变的不可避免。(Geogrpahy1.21)更重要的是,他第一次在制图实践中确立了“视点”,从而使曾经不可捉摸的形变得以在数学层面被精确地把控。通过对视点的选择,他进一步改变经纬线的呈现方式,以保留不同的真实比例,从而探索出更加相似以及合比例的制图效果。这在古代西方制图史上,无疑是一项伟大的创举。

视点的引入和确立,既代表了托勒密对埃拉托色尼之“赫尔墨斯视角”的传承,也是托勒密对前人未竟之数学理想的进一步开拓。托勒密借此将地理学完整地纳入了数学科学领域:就合比例而言,居住世界在平面化后仍保留中心和边界的真实比例,从而将整体形变控制在可接受范围内,而非如马里诺的矩形地图一样随纬度升高而愈加扭曲;([10],34页)就相似性而言,纬线乃至经线被呈现为圆弧,初步还原了现实中俯瞰球面的几何效果,亦是空前的创造性设计。两方面的成就将地理学擢升到足以在数学方面比肩天文学的位置。正如托勒密在卷一开头所言:“在地理学中,数学方法占据着绝对的优先性。我们首先必须要研究清楚大地的形状、大小和相对于周边的位置,从而描述出已知部分的范围和性质。另外,还应说明已知世界的各地分别位于哪一条天球纬线之下,以确定……相关的天象。这些部分归属于最崇高和最美好的智性追求……因为诸天的运转能大致为我们所见;然而大地却只能借助(再现的)图像得到认识。”(Geography1.1.8-9)([11],54-55页)

尽管天地呈现有诸多不同,托勒密还是努力地创造条件(譬如借助再现的图像),将地理学纳入一个整体的数学宇宙之中。这也反映出托勒密作品背后宏大的学术理想。早在天文学代表作《至大论》中,托勒密就表明了他的数学哲学立场:即相比于神学和物理学,“只有数学才能为它的信徒提供可靠而不可动摇的知识”,并使得追随者能够以神性相关的恒常、秩序与合比例来改造自身。[33]从这句话中,我们能看出作者不仅志在揭示恒常不易的秩序,更试图再现秩序以作用于世界或自身。在另一部著作《和音学》(Harmonics)中,这一意图体现得更加明确。他认为:“和音理性能产生听觉上的特定秩序,正如图像理性能产生视觉上的秩序,批判理性能产生思想上的秩序。”[34]随后他指出,和音学家不仅揭示和音现象背后的几何比例,也运用乐器复现它们以产生听觉上的秩序。类似地,地理学家也须基于图像理性揭示世界在“视觉上的秩序”,并通过绘制地图来再现这一世界秩序。因此,借助数学方法在地界构建清晰、稳定与合比例之秩序,正是《地理学》写作的应有之意。

正如该书英译者伯格伦所说,托勒密的制图法提供了“一个数学地理学家想象视角下的地球视图”。[35]而笔者更愿意将其称为“一个数学家基于想象视点构建的世界地理的几何秩序”。在再现世界秩序的过程中,“视点”扮演了枢纽性的角色:唯有通过想象的、超越的视点,我们身处其中的居住世界才可能被定量地观察和模仿,进而被赋予一种数学的理性秩序。在这一意义上,视点充当了某种“阿基米德支点”,托勒密借此得以将地理学纳入他以数学为万物确立秩序的宏大学术蓝图之中。

4 结 语

综上所述,作为以居住世界为描绘对象、以几何为基本方法的古代地理制图理论之大成者,托勒密《地理学》继承并实践了埃拉托色尼的“赫尔墨斯视角”,将古代西方制图理论推向了新的高度。为了在数学层面精确把控世界图像从球面到平面的转变,托勒密基于古希腊欧几里得的光学传统,构建了几何意义上的视点,借此将3种不同的数学方法加以综合,以在相似性与合比例性之间求取平衡。由此设计出的托勒密第一与第二制图法,也成为西方地理史上第一套系统性的几何制图理论。《地理学》对视点的运用,折射出背后以数学哲学为基础的制图思想。在他看来,数学是一切可靠知识的来源,地理学也须基于隶属于数学的图像理性再现居住世界的视觉秩序。在此基础上,视点构成了托勒密地理制图的独一无二的前提:唯有通过假定的视点,居住世界才可能被定量地观察和模仿,进而被赋予理性的几何秩序。因此,视点充当了托勒密构建地理世界的几何秩序、实现球面向平面转换的“阿基米德支点”。作为托勒密学术理想的一部分,视点的假定指向了一个更为宏大的数学世界图景,也使得托勒密制图在古代西方乃至世界制图理论史上占据了不可替代的一席之地。