具有群体防御和Allee效应的Leslie-Gower模型的定性分析*
2024-01-27曾彩焕李自尊梁思甜
曾彩焕,李自尊,梁思甜
(南宁师范大学 数学与统计学院,广西 南宁 530100)
Leslie-Gower型的食饵-捕食者模型如下
(1)
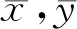
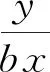

Ajraldi等[5]研究了食饵具有群体防御的模型,即当捕食者个体对食饵群体进行攻击时,食饵会聚集在一起进行防御,其功能响应以食饵密度的平方根为单位,这种群体行为对捕食系统的研究有着重大的作用.Maiti等[6]在[5]的基础上,研究了捕食者和食饵都具有防御功能的捕食系统,利用非线性近似的方法对原点附近的行为进行分析.Putra等[7]研究了具有群体行为的Leslie-Gower捕食模型,分析了系统的稳定性,结果表明改变初始条件和参数会使系统的稳定性发生改变.
(2)
为了简化系统,对模型(2)引入变换
得到
(3)
其中所有的参数均为正数.
1 系统的有界性
定理1系统(3)的解有界.
证明仿照文献[2]中定理4的证明方法.设(x(t),y(t))是系统(3)的任一解,则由系统(3)的第一个方程得
由Gronwall不等式可得


所以
令
由Gronwall不等式得
σ(t)≤L1+(σ(0)-L1)e-t,
故有
所以系统(3)的解是有界的.
2 平衡点分析
2.1 平衡点的存在性
系统(3)有灭绝平衡点E0(x0,y0)=(0,0),边界平衡点E1(x1,y1)=(1,0),E0和E1在任何参数条件下都存在.系统(3)的内部平衡点E*(x*,y*)满足

2.2 内部平衡点E*(x*,y*)的稳定性
定理2当ab<1时,E*(x*,y*)存在,定义
(4)

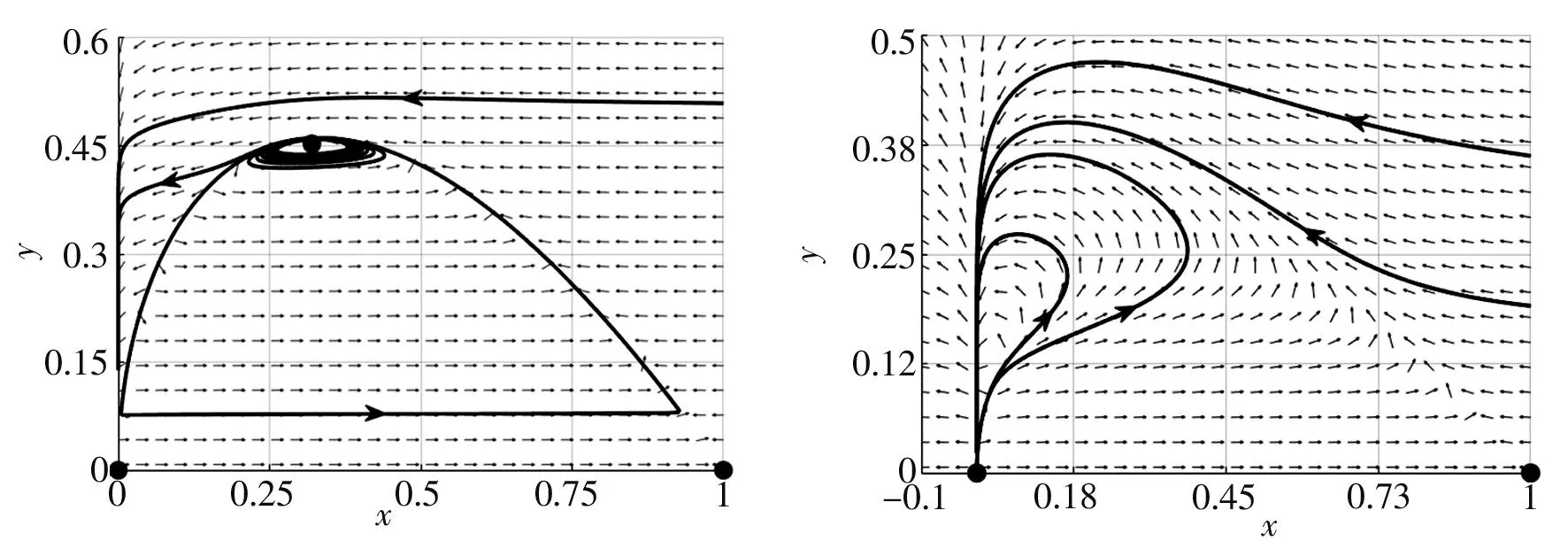
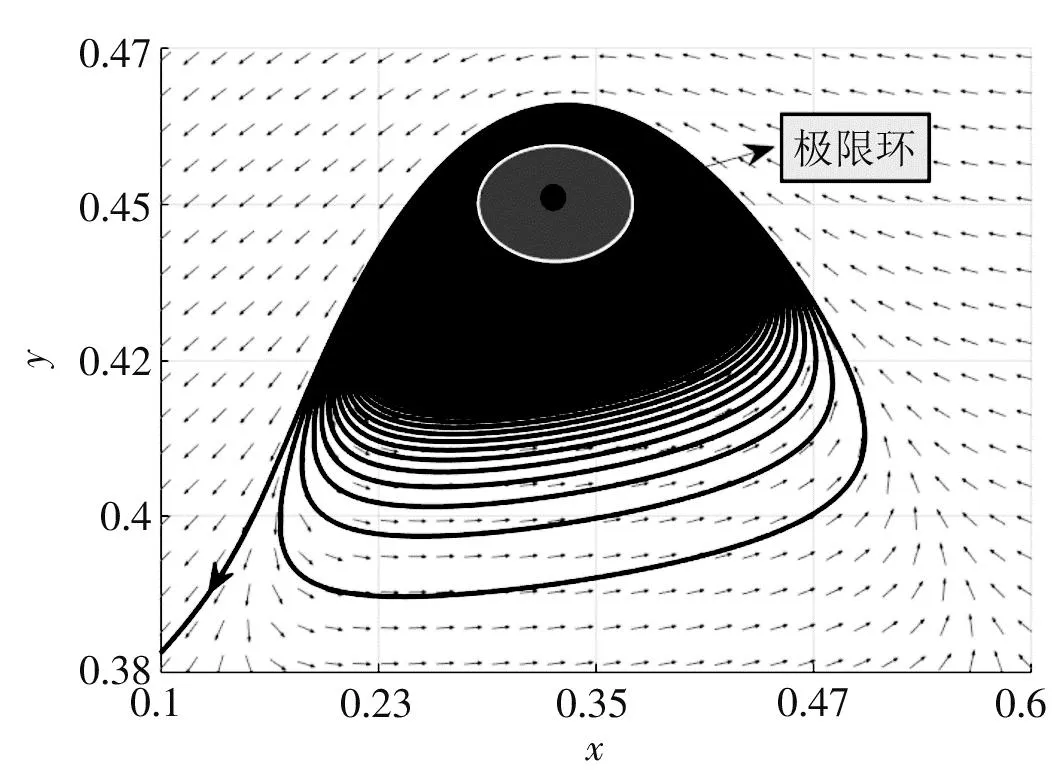
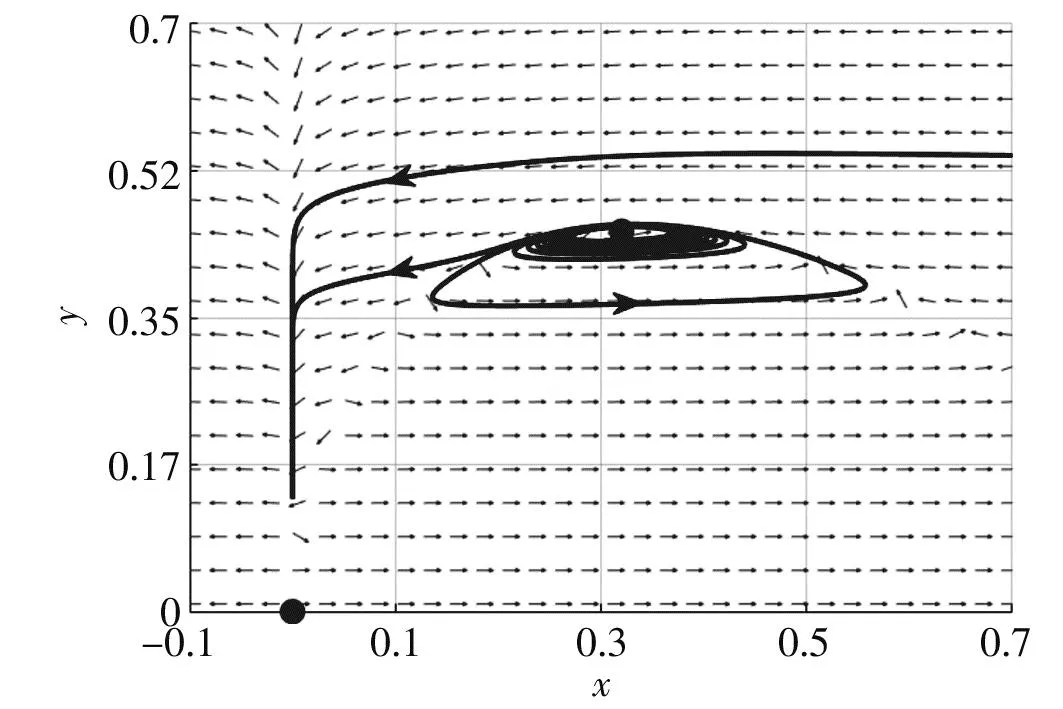
(1) 若B (2) 若B>B*,则E*(x*,y*)是不稳定的. 证明系统(3)的内部平衡点E*(x*,y*)的Jacobi矩阵为 (5) 特征方程为λ2-Pλ+Q=0,其中 因此有: (i) 若B (ii) 若B>B*,即P>0,则E*(x*,y*)是不稳定的. 定理3当1-2x-2s<0时,若E*(x*,y*)局部稳定,则E*(x*,y*)是吸引的. 证明当1-2x-2s<0时有 根据Bendixon判据可知系统(3)无周期轨,所以E*(x*,y*)是吸引的. 定理4系统(3)的平衡点E1(1,0)是鞍结点. 证明系统(3)在(1,0)处的Jacobi矩阵为 其特征值为λ1=-1,λ2=0.作变换X=x-1,Y=y-1,再二阶Taylor展开,则系统(3)转换为系统 (6) 其中P1(X,Y)和Q1(X,Y)是满足i+j≥3的幂级数项xiyj. 作变换X=ax+y,Y=-y,则系统(6)变为 (7) 其中P2(x,y)和Q2(x,y)是满足i+j≥3的幂级数项xiyj. 令τ=-t,得 (8) x=-By2+ABy3+o(y4), s=0.04,B=0.5下的相图 从而得到 图1 系统(3)在参数a=0.85,b=0.8, 我们通过对系统(3)作变换来研究它在E0处的稳定性,给出了以下定理. 定理5E0附近的轨线当ab<1时由稳定结点和鞍点组成,当ab≥1时由稳定结点和封闭轨线组成. (9) (10) 系统(10)在(0,0)处的Jacobi矩阵为 其特征根为0,可知平衡点(0,0)是高阶奇点.接下来利用“吹胀”的方法来研究高阶奇点附近的轨线结构.对(0,0)作沿X与Y方向的“吹胀”变换,相当于把流形上的计算转移到坐标卡上,接下来分别在X方向的坐标卡和Y方向的坐标卡进行分类讨论[9]. 在坐标卡{x=1}上令X=r,Y=ry,dτ=rdt,则系统(10)变为 (11) 其中P1(r,y)是满足i+j≥3的幂级数项xiyj,Q1(r,y)是满足i+j≥4的幂级数项xiyj. (c) 坐标卡{y=1} (d) 坐标卡{y=-1} (a) 坐标卡{x=1} (b) 坐标卡{x=-1} (c) 坐标卡{y=1} (d) 坐标卡{y=-1} 在坐标卡{x=-1}上令X=-r,Y=ry,dτ=rdt,则系统(10)变为 (12) 其中P2(r,y)是满足i+j≥3的幂级数项xiyj,Q2(r,y)是满足i+j≥4的幂级数项xiyj. 在坐标卡{y=1}上令X=rx,Y=r,dτ=rdt,则系统(10)变为 (13) 其中P3(r,x)和Q3(r,y)是满足i+j≥4的幂级数项xiyj. 在坐标卡{y=-1}上令X=rx,Y=-r,dτ=rdt,则系统(10)变为 (14) 其中P4(r,x)和Q4(r,x)是满足i+j≥4的幂级数项xiyj. 利用以上结果可得到4张坐标卡上的图形,然后转换到单位圆周外一个邻域内的图形,如图4(a)和图5(a)所示.最后把单位圆周缩到坐标原点,得到XOY平面上(0,0)附近的轨线,如图4(b)和图5(b)所示. (a) 系统(10)“吹胀”后的轨线结构 (b) 系统(10)缩回原点的轨线结构 由图4和图5可知,系统(10)当ab<1时在(0,0)附近的轨线由稳定结点和鞍点组成,当ab≥1时在(0,0)附近的轨线由稳定结点、鞍点和封闭轨线组成. 系统(3)与系统(10)的相图在第一象限内拓扑同胚,数值模拟结果如图6所示.当ab<1时,轨线最终会落在y轴上,捕食者和食饵的数量逐渐减少,最终趋于灭绝;当ab≥1时,内部平衡点消失,无论捕食者和食饵的初始值是多少,两个种群最终都会趋于灭绝. (a) 参数a=0.85,b=0.8,s=0.04,B=0.5 (b) 参数a=1.5,b=1,s=0.5,B=0.5 证明当ab<1时系统(3)存在内部平衡点E*(x*,y*).计算得 由上述结论可知系统(3)在E*处发生Hopf分岔. 接下来计算系统(3)的第一Liapunov系数,以研究其Hopf分岔的稳定性. 作变换X=x-x*,Y=y-y*,将平衡点E*(x*,y*)移到原点处,再在原点处泰勒展开到三阶,则系统(3)转变为 (3)' 其中, P1(X,Y)和Q1(X,Y)是满足i+j≥4的幂级数项xiyj. 根据文献[10]中的公式(3),系统(3)'的第一Liapunov系数为 其中Δ=a10b01-a01b10>0. 由上述分析可得以下结论:若σ>0,则E*(x*,y*)的Hopf分岔是亚临界的,产生一个不稳定的极限环;若σ<0,则E*(x*,y*)的Hopf分岔是超临界的,产生一个稳定的极限环. 图7 系统(3)在参数a=0.85,b=0.8,s=0.04,B=0.4下的相图 图8 系统(3)在参数a=0.85,b=0.8,s=0.04,B≈0.4525下的相图 图9 系统(3)在参数a=0.85,b=0.8,s=0.04,B=0.5下的相图 本文研究具有Allee I效应和食饵群体防御行为的Leslie-Gower捕食模型.证明了系统解的有界性,并分析了平衡点的存在性与稳定性.利用“吹胀”的方法来研究高阶奇点附近的轨线结构,并给出了跨临界分岔以及Hopf分岔的条件.通过计算系统的第一Liapunov系数来判断Hopf分岔的稳定性.最后用数值模拟验证了理论结果的正确性. 由上述分析可知,只有当捕食者的Allee效应阈值满足条件 时,系统(3)中的两个种群才能共存.如果Allee效应的阈值过大,捕食者的增长速率会变小,种群数量会下降直至灭绝.这意味着当捕食者种群受到Allee效应的影响较小时,捕食者更容易生存,并与食饵种群达到共同存活的稳定状态.所以,捕食者受到Allee效应的影响越小,对种群的多样性越有益.2.3 边界平衡点E1(x1,y1)的稳定性


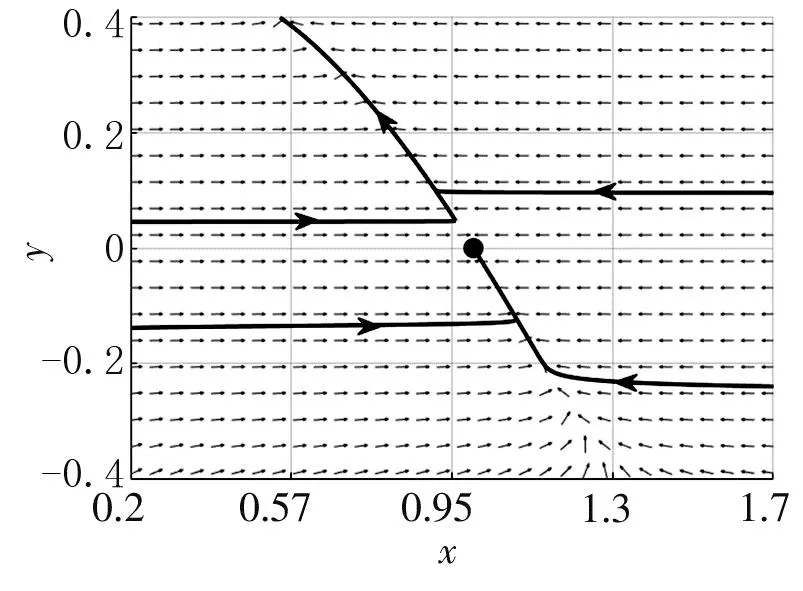
2.4 灭绝平衡点E0(x0,y0)的稳定性

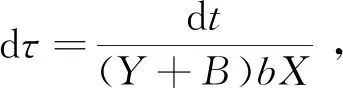
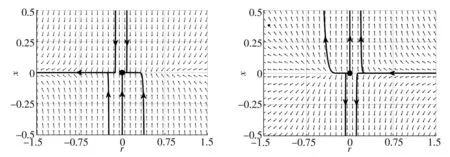





3 分岔分析
3.1 跨临界分岔


3.2 Hopf分岔
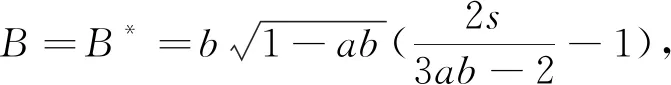
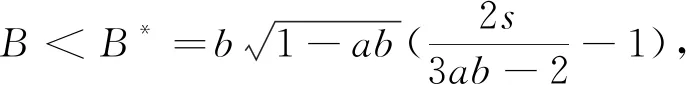

4 结论
