基于熵权TOPSIS的革命老区乡村振兴评价模型及实证

邢柏棋 于相伟 王茂彬 范兴奎

摘 要：本课题围绕革命老区以“三农问题”为核心的乡村振兴战略的总要求，通过收集整理革命老区发展状况数据，基于数学建模思想建立熵权TOPSIS模型对数据定量分析，构建革命老区乡村振兴科学评价体制。帮助全方位展示和动态掌握各地革命老区乡村振兴战略的推进进程；发现革命老区乡村振兴战略推进中的薄弱环节，对进一步分析预测乡村振兴战略前景、有针对性地调整革命老区乡村振兴战略各项规划具有重要意义。

关键词：“三农”问题；乡村振兴；熵权TOPSIS法

中图分类号：F323.8    文献标识码：A 文章编号：1005-6432（2024）01-0027-07

DOI：10.13939/j.cnki.zgsc.2024.01.007

1研究目的

1.1 探索建立功能完善、科學合理、可操作性强的统计监测指标体系

乡村振兴战略是围绕新时代“三农”问题，加快农业农村现代化步伐，加快推动我国农业大国向农业强国迈进的重大战略举措。探索建立功能完善、科学合理、可操作性强的统计监测制度，对全方位展示革命老区乡村振兴战略落地落实的状态、动态掌握各地革命老区乡村振兴战略推进的进程、发现革命老区乡村振兴战略推进中的薄弱环节、分析预测乡村振兴战略前景、有针对性地调整革命老区乡村振兴战略各项规划具有十分重要的意义［1］。

1.2 借助于数学模型构建革命老区乡村振兴评价理论体系

本课题围绕革命老区乡村振兴战略的总要求，针对革命老区总体目标任务及阶段安排，对生态指标、文明指标、管理指标、发展指标、红色文化指标等进行多元化评价和综合分析，遴选老区实施乡村振兴战略的科学性、建设性、可量化、可操作性的统计指标。借助于数学模型构建革命老区乡村振兴评价体系，通过数据分析定量地对革命老区乡村振兴进行深入的理论研究，这无疑对革命老区将乡村振兴战略落到实处具有十分重要的现实意义［2-3］。

2 研究现状

2.1 国内乡村振兴监测指标体系发展和研究现状

中国共产党始终高度重视“三农”问题，重视革命老区的乡村振兴工作。通过对国内有关文献的整理和分析，发现对于乡村振兴战略的规划与发展大多数是关于三农问题的本身研究，而对乡村振兴的研究刚刚提上日程，更没有形成完善有效的革命老区乡村振兴的理论评价体系。这样关于乡村振兴科学的评价研究就更具有重大而紧迫的现实意义。

2.2 国外乡村振兴监测指标体系发展动态

农村发展问题是各国急需解决的难题，作为当今世界重要的课题，国外对于农村的振兴有一定的评价标准。在现代化测评方面，比较有代表性的是英克尔斯评价指标体系，该评价体系由人均国民生产总值、农业产值占国内生产总值的比重、农业劳动力占总劳动力的比重、成人识字率等指标组成。英克尔斯的标准简洁明了，运用数据定量衡量农村发展振兴现状，可操作性强，具有很强的实用性。除此之外，谢尔登和康维尔斯的社会变迁指标对农村发展评价体制也有重要影响。由此可以看出，西方对于农村振兴评价机制问题有颇丰的研究成果。

3 乡村振兴评价机制——熵权TOPSIS法构建

在选取科学和系统的指标体系的基础上，运用熵权法求得指标的权重，运用TOPSIS法，借助指标的权重和数据，求得每个革命老区乡村振兴政策实施的评分，进而可以直观看出乡村振兴政策的实施效果，并依据该评价机制发现问题，及时调整政策。

3.1 评价乡村发展程度指标和研究对象的选取

在指标选取的过程中，应遵循系统性和全面性、科学性和实用性、先进性和可操作性以及符合总体要求的原则。

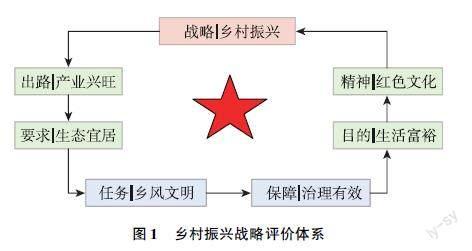
党的十九大剔除实施乡村战略的总体要求，即“产业兴旺、生态宜居、乡风文明、治理有效、生活富裕”，从产业兴旺切入到生活富裕结局构成了一个完整的目标。其中产业兴旺是乡村振兴的根本出路，生态宜居是乡村振兴的内在要求，乡风文明是乡村振兴的紧迫任务，治理有效是乡村振兴的重要保障，生活富裕是乡村振兴的主要目的。

综上所述，根据当代国家和政府对于乡村振兴战略的规划和要求，对相关性强的指标利用聚类等数学方法，优化指标选取。

本课题选取产业兴旺、生态宜居、乡风文明、治理有效、生活富裕以及红色文化等六个维度作为准则层，选取高标准农田占比、农业机械化水平、农业土地产出率、农村居民恩格尔系数、村庄绿化覆盖率、农村无害化厕所普及率、农业科技进步贡献率、历史文化价值等30个指标作为指标层，构建革命老区乡村振兴综合评价体系［8-12］，下面是对综合评价模型中维度层指标的选取，如表1所示。

针对研究对象的选取，根据查阅文献资料和实地走访调查，并重点参考中共中央民政部下发关于革命老区的判定标准等相关文件，选取15个具有深厚红色文化底蕴和革命历史的老区作为研究对象，如江西省的瑞金、黑龙江省的巴彦、山东省的临沂。

3.2 指标数据收集与整理

根据选取的革命老区和指标层，在国家统计年鉴、中国农业农村部等官方网站收集数据。对每个指标数据均选取最新数据或各省统计平均数据，保证了数据集的真实性和时效性，乡村振兴监测体系结果更加真实有效。

3.3 熵权TOPSIS评价模型

熵权TOPSIS法充分利用原始数据信息的同时剔除主观性，结合指标层的权重系数、评价对象指标层数据距离理想解的差距，对评价对象即革命老区进行评分，从而达到乡村振兴政策监测的目的，通过定量分析和精确评估结果，更好地调整和完善乡村振兴工作。

3.3.1 对指标数据的标准化处理

重点对指标数据建立初始矩阵A=（wtj）， 其中，wij表示第t个革命老区的第j个初始值标值。利用模糊隶属度对指标进行标准化。通过指标标准化处理，将原始数据的值控制在0～1，即相较于原始数据，其具有相同的尺度，在熵权TOPSIS法中对于指标熵权的确定和每年乡村振兴政策实施效果的评价更加客观合理。

对于指标的标准化分为正向标准化和负向标准化。其中正向化指标是指该指标值越大，表示乡村振兴政策落实越完善。负向化指标相反。针对本课题指标，除城乡居民收入比和农村居民恩格尔系数为负向化指标，其余指标都为正向化指标。根据此方法，设ytj为第j个评价对象第t个指标标准化后的值；n为被评价的对象数，则可通过正向化指标标准化公式（1）、负向化指标标准化公式（2）对指标进行标准化。

ytj=wtj－min1≤j≤nwtjmax1≤j≤nwtj－min1≤j≤nwtj（1）

ytj=max1≤j≤nwtj－wtjmax1≤j≤nwtj－min1≤j≤nwtj（2）

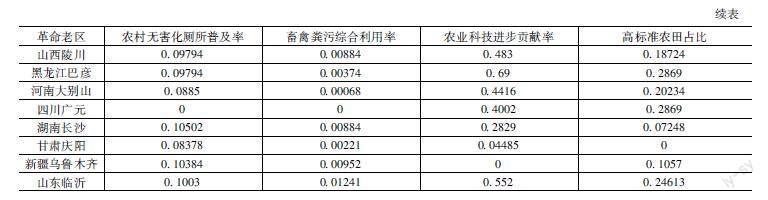
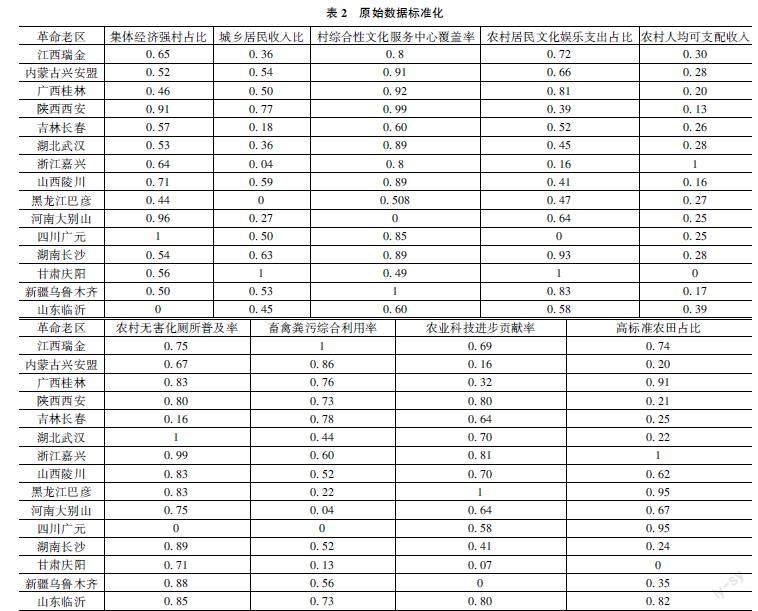
借助原始收集的指標数据，根据上述数据标准化处理方式，对数据进行预处理，指标数据进行预处理后部分展示如表2所示。

3.3.2 乡村振兴评价体系指标的熵值

根据乡村振兴评价体系对革命老区振兴工作评价的定量要求，并综合考虑指标之间的相互独立性，运用熵权法对指标的熵值进行确定。在信息论中，熵是对不确定性的一种度量。不确定性越大，熵就越大，包含的信息量就越大。在熵权法中，可以运用熵值的特性来判断乡村发展程度指标的离散程度，指标离散程度越大，该指标对乡村振兴评价体系的影响程度越大，即权重越大。这种对指标重要程度定量化的确定，精确度较高，客观性较强。结合指标收集的实际情况与指标之间的关系，在30个指标中选取9个数据来源准确、具有长远发展的目标作为评价指标体系，如高标准农田占比、无害化厕所普及率、居民文化娱乐支出占比等。熵权指标层构成体系如图2所示。

图2 乡村振兴监测指标体系

判定指标对应熵值和权重系数的公式如下：

设ej为第j个指标的熵值，pij为第i个系统中的第j项指标的特征比重。

pij=wtj∑ni=1wtj  ej=－1lnn∑ni=1pijlnpij（3）

式中，∑ni=1wtj为第j个指标的所有系统观测数据之和。

设指标j的差异系数为gj，30个指标权重系数为sj，公式表示如下：

gj=1－ejsj=gj∑30j=1wtj（4）

借助预处理指标数据，运用Python软件计算指标的差异系数和权重系数，结果如表3所示。

通过观察指标权重系数可知，高标准农田占比权重系数最大，在乡村振兴评价体系中影响程度最大，最重要。畜禽粪污综合利用率权重系数最小，对评价体系影响最小，重要程度较低。此结果有熵权值的概念得到印证，在原始数据中，各革命老区高标准农田占比指标数据差异度较大，即数据离散程度大，因此权重系数高。相反，畜禽粪污综合利用率指标数据差异度较小，离散程度较小，因此该指标权重系数较小。

3.3.3 革命老区乡村振兴评价得分

为定量地反映革命老区的乡村振兴发展指数，由指标数据和指标权重相乘，可以确定各指标数据加权值，强调了各指标重要程度的区别，优化完善了乡村振兴评价机制。设yij为第i个革命老区第j个指标标准化数据的加权值，wij为第i个革命老区的第j个指标观测值规范化处理后的值，sj为权重系数，根据上述加权方法可知：

yij=wijsj（5）

借助标准化后的指标数据和指标权重，可计算出评价指标加权后的数据矩阵，结果如表4所示。

结合评价体系的实际情况，采用TOPSIS法衡量各革命老区发展指标与理想解的贴近度。在指标体系中，挑选正向评价指标的最大值、负向评价指标的最小值组成评价体系中理想最优解，反之组成最劣解。理想最优解和最劣解也就是正负理想解。设y+j为第j个指标观测数据的最大值，y－j为第j个指标观测数据的最小值，j=1，2，…，30。

y+j=max1≤k≤nwkj  y－j=min1≤k≤nwkj（6）

按照最优理想解和最劣解公式，运用Python计算出：

y+j=［1.1.1.1.1.1.1.1.1］

y－j=［0.31 0.56 0.76 0.4 0.32 0.58 0.60 0.5 0.29］

计算出评价系统，即各个革命老区加权指标数值与正负理想解的欧式距离。在这里引入欧式距离，可以定量地反映某个革命老区与达到最理想的乡村振兴实施目标的差距。设d+i为第i个革命老区与正理想解的欧式距离，d－i为第i个革命老区与负理想解的欧氏距离，则：

d+i= （y+1－yi1）2+（y+2－yi2）2+…+（y+30－yi30）2（7）

d－i= （y－1－yi1）2+（y－2－yi2）2+…+（y－30－yi30）2（8）

借助以上公式可计算得到各革命老区对应的到正负理想解的距离：

在乡村振兴评价系统中，为定量地衡量各革命老区发展情况，即革命老区乡村振兴发展指数，引入相对贴近度的概念，设fi为第i个革命老区各自指标体系到正理想解的贴近度，fi值为各革命老区的乡村振兴发展指数。公式为：

fi=d－id－i+d+i（10）

式中，i=1，2，…，n。针对该乡村振兴发展指数，若革命老区的指标体系距正理想解距离近，距负理想解距离远，则fi→1，其乡村振兴发展指数较高，反之，fi→0，其乡村振兴发展指数较低。由此，按照fi值从大到小对各革命老区进行高低排序。fi值越大，排名越靠前，表示该革命老区乡村振兴发展水平越高；fi值越小，排名越靠后，表明该革命老区乡村振兴发展水平越低。

借助指标标准化后的数据和权重，运用Python软件对革命老区的得分进行求解，最终得出得分即乡村振兴评价指数结果，如表6所示。

分析以上革命老区得分即乡村振兴评价指数可知，浙江嘉兴的得分最高，其次是黑龙江巴彦、江西瑞金，得分处于中间的有山东临沂、河南大别山，最后是甘肃庆阳与吉林长春。

4 乡村振兴评价体系的分析与建议

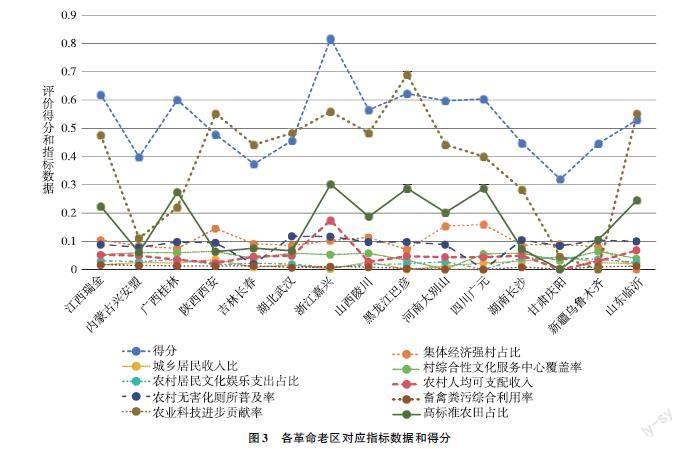
根据熵权TOPSIS法对乡村振兴评价监测体系的构建，得出的指标权重系数和革命老区的评价指数，可以定量地分析得分高的革命老区发展长处、得分低的革命老区发展不足之处，从而得到更为全面系统的发展建议。为直观看出各革命老区指标数据和最终得分结果，运用折线图形式进行展示，如图3所示 。

图3 各革命老区对应指标数据和得分

借助此折线图分析，针对评价指标，高标准农田占比和农业科技进步贡献各革命老区之间差别较大，数据离散程度较大，其他指标相反。针对得分，可以看出浙江嘉兴和江西瑞金排名较高，甘肃庆阳和内蒙古兴安盟排名较低。

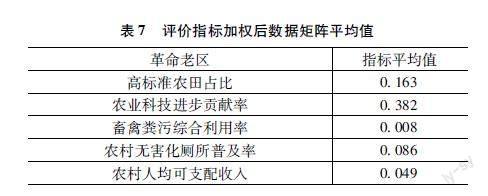
为方便判断各革命老区的指标数据水平，对各指标对应的数据求出其平均数，结果如表7所示。

重点借助革命老区浙江嘉兴对应的标准化后指标数据和权重可知，其所有指标数据都在平均值以上。通过表4和表7的数据可知，针对权重最高的高标准农田占比指标，其对应的加权后指标数值0.302远高于平均值0.163。同样，对于权重其次的农业科技进步贡献率其加权后指标数值0.558也远高于平均数值0.382。其次，统筹分析其全部加权后指标数值，浙江嘉兴革命老区是最接近TOPSIS法中正理想解即最优理想解；并且对于权重最小的畜禽粪污综合利用率，其加权后指标数值也高于平均数值。综合以上情况，在乡村振兴评价监测体系中，浙江嘉兴得到最高评分。加之，浙江嘉兴处于中国当今经济最发达的长江三角洲地带，气候温暖潮湿，适宜农业生产的发展，是最有发展潜力的革命老区。因此在乡村振兴政策实施过程中，需要重视权重系数高的指标，如大力开发高标准农田，将耕地的产出率提升。并且，加大投入对农业科学技术的研发、提高农业科技进步贡献率可提升农业生产产量，降低人工成本。这样，可以有规划地提升革命老区在乡村振兴评价监测体系的评价指数。

用相同的方式和思路对得分最低的甘肃庆阳进行分析，对于权重较高的高标准农田占比，其加权后指标数值为0，也就是在所有革命老区中处于最低水平。对于農业科技进步贡献率来说，甘肃庆阳革命老区的指标数值远低于平均值（也就是其综合分析所有加权后对应的指标数值），可以看出指标数值距离最优理想解最远，较为贴近最劣解。这也是其评分最低的主要原因。其在乡村振兴发展中也有成果，禽畜粪污综合利用率和村综合性文化服务中心覆盖率较高，比较贴近于最优理想解数值。但是，这两个指标在权重系数上处于较低水平，因此也是评价指数不高的原因之一。而且，相比于浙江嘉兴，甘肃庆阳位于较偏远的西部，大部分地区气候高寒、多风沙，环境较为恶劣，不利于农业的发展，整体经济水平较低。因此应着重根据当地的自然环境和人文条件，大力提高能有效适应当地多风沙环境的高标准农田占比，并且根据当地财政能力，多向农业技术发展方向投资，提升科技进步对农业生产的贡献。并根据此评价体系，在维持当前水平前提下，适当减少对畜禽粪污综合利用的发展和村综合性文化服务中心的建设。

同样，对于评分处于中间水平的山东临沂和河南平顶山，其指标数值不论是对于权重高还是低的指标都是处于平均值。且两地都是处于中原地区，气候和经济条件相似具有相似的发展前景。针对这两个革命老区，应在维持当前状况下，尽力发展每一项指标，向评分最高的浙江嘉兴靠拢。

参考文献：

［1］黄莉，邓诗靖，周芷秀，等.基于G1-熵权法的地域性红色文化旅游资源评价指标体系构建［J］.宁德师范学院学报（哲学社会科学版），2021，139（4）：42-50.

［2］顾凤岐，王爽．构建社会主义新农村指标体系研究［J］．统计与信息论坛，2006（5）.

［3］秦艳.我国乡村振兴的目标评价体系构建研究［D］.厦门：厦门大学，2018.

［4］中国统计信息网［EB/OL］.www.tjcn.org.

［5］龚纯，王正林.MATLAB语言常用算法程序集［M］.北京：电子工业出版社，2010.

［6］司守奎，孙玺菁.数学建模算法与应用［M］.北京：国防工业出版社，2011.

［7］张琴，王晓晴，李莉莉.乡村振兴统计监测指标体系的构建研究［J］.青岛大学学报（自然科学版），2022，35（1）：112-116.

［8］徐海丽.广西实施乡村振兴战略的统计监测指标与方法［J］.改革与战略，2019，35（6）：86-103.

［9］李刚，迟国泰，程砚秋.基于熵权TOPSIS的人的全面发展评价模型及实证［J］.系统工程学报，2011，26（3）：400-407.

［10］杨惠敏，付萍.基于熵权的多级模糊综合评价的应用［J］.北京：华北电力大学学报，2005，32（5）：104-107.

［11］迟国泰，曹婷婷，张昆.基于相关-主成分分析的人的全面发展评价指标体系构建［J］.系统工程理论与实践，2012，32（1）：111-119.

［12］范兴奎，闫洁，宋善洋.基于模糊评价的深圳市人才吸引力水平研究［J］.牡丹江师范学院学报（自然科学版），2019（106）：10-14.