自抗扰开关磁阻电机转速控制器的快速参数整定方法

摘 要：线性自抗扰控制（LADRC）器设计简单且性能优秀，但控制器参数的优化设计过程比较复杂。针对此问题，提出一种LADRC的快速参数整定方法，以实现控制器参数的快速优化设计。首先，建立并化简一阶模型辅助LADRC系统的数学模型；其次，利用频域特性分析方法详细地分析控制器参数和控制系统关键性能的定性及定量关系，如系统的稳定性、跟随性能、抗干扰能力、噪声抑制能力和对象参数鲁棒性，并提出基于控制器性能优化的快速参数整定方法。在此基础上，以开关磁阻电机转速控制器为研究对象，利用所提出的快速参数整定方法快速获取控制器参数。实验结果证明所设计的控制器有较好的抗干扰能力和鲁棒性，该方法对于LADRC有很好的工程实用价值。

关键词：线性自抗扰控制；参数整定；频域分析；鲁棒性；转速控制；开关磁阻电机

DOI：10.15938/j.emc.2024.11.011

中图分类号：TM352

文献标志码：A

文章编号：1007-449X（2024）11-0117-10

Rapid parameter tuning method of LADRC applied in switched reluctance motor speed regulation

LI Yiqian， MA Qishuang， XU Ping

（School of Automation Science and Electrical Engineering， Beihang University， Beijing 100191， China）

Abstract：Linear active disturbance rejection control （LADRC） possesses the unique advantage of simplified controller design and excellent performance， but the relationship between controller parameters and system performance is very complex. A rapid parameter tuning method for LADRC was proposed to realize quick design of the controller parameters based on performance optimization of the control system. Firstly， model of a first-order model-assisted LADRC system was built up and simplified. Detailed parametric analysis in frequency domain was then implemented to discuss main features of the system including stability， following performance， anti-disturbance ability， noise reduction ability and robustness. Furthermore， the proposed rapid parameter tuning method was introduced and the controller parameters in speed regulation of a switched reluctance motor control system were obtained rapidly， which were verified to be reasonable by later experiments. The proposed method is proved to be effective in practical disturbance rejection and robustness on the plant characteristics. The work is helpful to promote the engineering application of LADRC.

Keywords：linear active disturbance rejection control; parameter tuning; frequency domain analysis; robustness; speed control; switched reluctance motor

0 引 言

自抗扰控制（active disturbance rejection control，ADRC）采用主动抗扰的控制策略，其核心思想是将控制系统内外的所有不确定性干扰和动态过程视为系统的一个扩张状态，并在控制律中对其进行补偿^[1]。随着相关理论的逐渐成熟，ADRC已成功应用于各种领域并表现出优异的性能^[2-]。但 ADRC仍存在一个不可忽视的问题，即控制器的参数设计过程非常复杂。其中，线性自抗扰控制（linear active disturbance rejection control，LADRC）的参数整定问题相对简单且易于数字化实现^[4]，因此LADRC在工程实践中获得了越来越多的应用。

目前，LADRC已被用于解决电机控制领域的各种问题^[5-7]，其控制器的参数整定是控制系统性能优化的必要且关键环节。为此，文献[4]提出一种基于 “极点配置”的LADRC参数设计思路，其主要思想是利用带宽配置控制器的闭环极点，并将控制器的参数表示为带宽的函数。显然，对于控制器参数较多的情况，这种基于带宽的控制器参数设计方法可以在很大程度上简化控制器的参数整定过程。

文献[8]基于“极点配置”法分析一阶/二阶LADRC系统的观测器带宽对闭环系统稳定性的影响，并较为详细地论证控制系统稳定性对于被控对象的参数具有较强的鲁棒性。对于更特殊的应用需求，文献[9]提出一种基于查表法的LADRC控制器带宽参数的快速设计方法，并论述采用该方法时控制系统可以满足给定的剪切频率和稳定裕度指标。为了进一步优化LADRC的带宽参数，文献[10]分别从时域和频域角度分析LADRC系统的抗干扰能力，并通过仿真讨论两种带宽参数的比值对系统稳定性的影响。对于高阶或复杂的控制对象，LADRC的参数数量增加，这使得控制器的参数整定过程更加复杂。为此，文献[11]设计一个二阶线性自抗扰控制器使系统输出与给定相近似的频域特性，其控制器的带宽参数可利用数值方法求解最小二乘方程获得。该方法实现简单，但需要被控对象精确的数学模型，因此在许多应用场合中较难实现。上述文献分别从不同角度对自抗扰控制器的带宽参数进行优化，但仍缺乏对控制系统综合性能的分析。

除了上述基于带宽的参数整定方法，人工智能算法也被用于复杂的非线性或线性自抗扰控制器的参数整定^[12]，其思想是首先根据系统不同方面的性能需求设计一个合理的目标函数，然后可以采用遗传算法（genetic algorithm，GA）或其他自学习算法来求解最优的控制器参数^[1]。该方法的难点在于目标函数的设计比较复杂。除此之外，文献[14]中还介绍了通用形式自抗扰控制器和传统PID控制器的参数等效方法。该方法可以基于已有的PID控制器实现自抗扰控制器的快速设计，但两种控制器的性能只能在特定限制条件下近似等效^[15]。

综上所述，结合被控对象的特点并针对一种或多种性能优化的LADRC系统的参数整定问题仍需进一步研究。本文在上述研究的基础上，提出一种LADRC参数的快速整定方法，该方法包括LADRC系统模型的简化、系统性能的详细分析以及基于系统性能优化的快速参数设计。本文最后将该方法应用于开关磁阻电机（switched reluctance motor， SRM）的LADRC转速控制器的参数整定中，实验结果证明了该方法的有效性。

1 模型辅助LADRC系统的模型简化

1.1 LADRC的基本模型

对于一个n阶被控对象可以描述为：

x^（n）=f（x，d（t））+bu；y=x。（1）

式中：x为对象的状态变量；u和y分别为输入和输出；b为描述对象特性的系数。系统可能受到总扰动f包含外部扰动d（t）以及对象参数的不确定性影响。

对于一个n阶对象，通常可以构造一个n阶的自抗扰控制器。自抗扰控制器利用扩张状态观测器（extended state observer， ESO）估计系统状态和扰动，这体现了自抗扰控制是主动对干扰进行观测和抑制的。并且由于扰动是从系统输出中可观的，必然可以构建合适的扩张状态观测器实现对扰动的实时估计。对于n阶系统，常用的线性扩张状态观测器（linear extended state observer，LESO）表示为：

z·1=z2－h1（z1－y）；

z·n=zn+1－hn（z1－y）+b0u；

z·n+1=－hn+1（z1－y）。（2）

式中：h1，…，hn+1为LESO的增益系数；b0为控制补偿增益系数，取系数b的估计值。

自抗扰控制的核心在于利用观测的扰动对原控制对象进行动态化补偿，使其近似等效为纯积分串联型对象，即y^（n）≈u0，从而具有更简单的控制特性。不难证明，对于纯积分串联型被控对象，线性误差反馈控制律可实现较好的控制效果，从而简化控制律的设计，即：

u0=kp1（v－z1）+…+kpn（v^（n－1）－zn）；

u=u0－zn+1b0。（3）

式中：v为控制系统的给定输入；kp1，…，kpn为误差反馈控制律的增益系数。

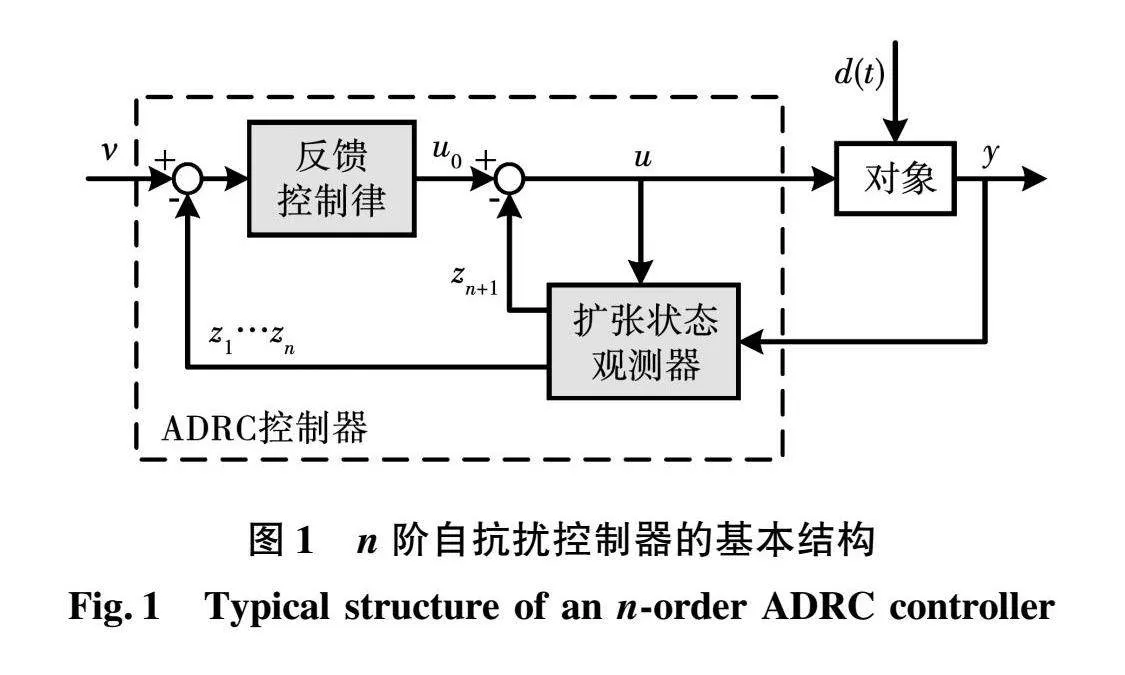
综上所述，n阶ADRC系统的基本结构如图1所示，控制器的待整定参数共有2n+1个，因此一个实用且快速的参数整定方法是十分必要的。

1.2 模型辅助LESO及其观测误差分析

对于大多数的应用场合，可以很容易通过测量或其他建模方法获得被控对象的粗略模型，因此可以利用被控对象已知的模型信息设计模型辅助扩张状态观测器（model-assisted ESO，MESO），从而提高观测器对未知扰动的估计能力。

本文分析的一阶对象表达式为：

x·=－ax+f+bu；

y=x。（4）

式中对象参数a近似已知，总扰动f仅描述了系统受到的不确定性外部扰动以及对象参数a建模不准确造成的影响。

同样地，可建立一阶控制系统的模型辅助扩张状态观测器和误差反馈控制律，结果分别为：

z·1=z2－h1（z1－y）－az1+b0u；

z·2=－h2（z1－y）。（5）

u=kp（v－z1）－z2+az1b0。（6）

扩张状态观测器能否准确地估计系统状态和扰动直接影响自抗扰控制器的性能。定义观测器的误差向量为ε=x-z，可得误差方程为

ε·=－2a－h11－h20ε+01f·Pε+Ef·。（7）

参考LESO参数的带宽整定方法，配置二阶观测器的两个极点均在观测器带宽ωo上，则h1=ωo-a和h2=ω2o。对于f·=0的情况，易得上述观测误差总能收敛至零。而对于更一般的情况，通常可假设f为阶跃函数形式的扰动，则可求得零初始观测误差下MESO的观测误差为

ε（t）=δte^－ωot（ωot+1）e^－ωot。（8）

式中δ为阶跃扰动的幅值。

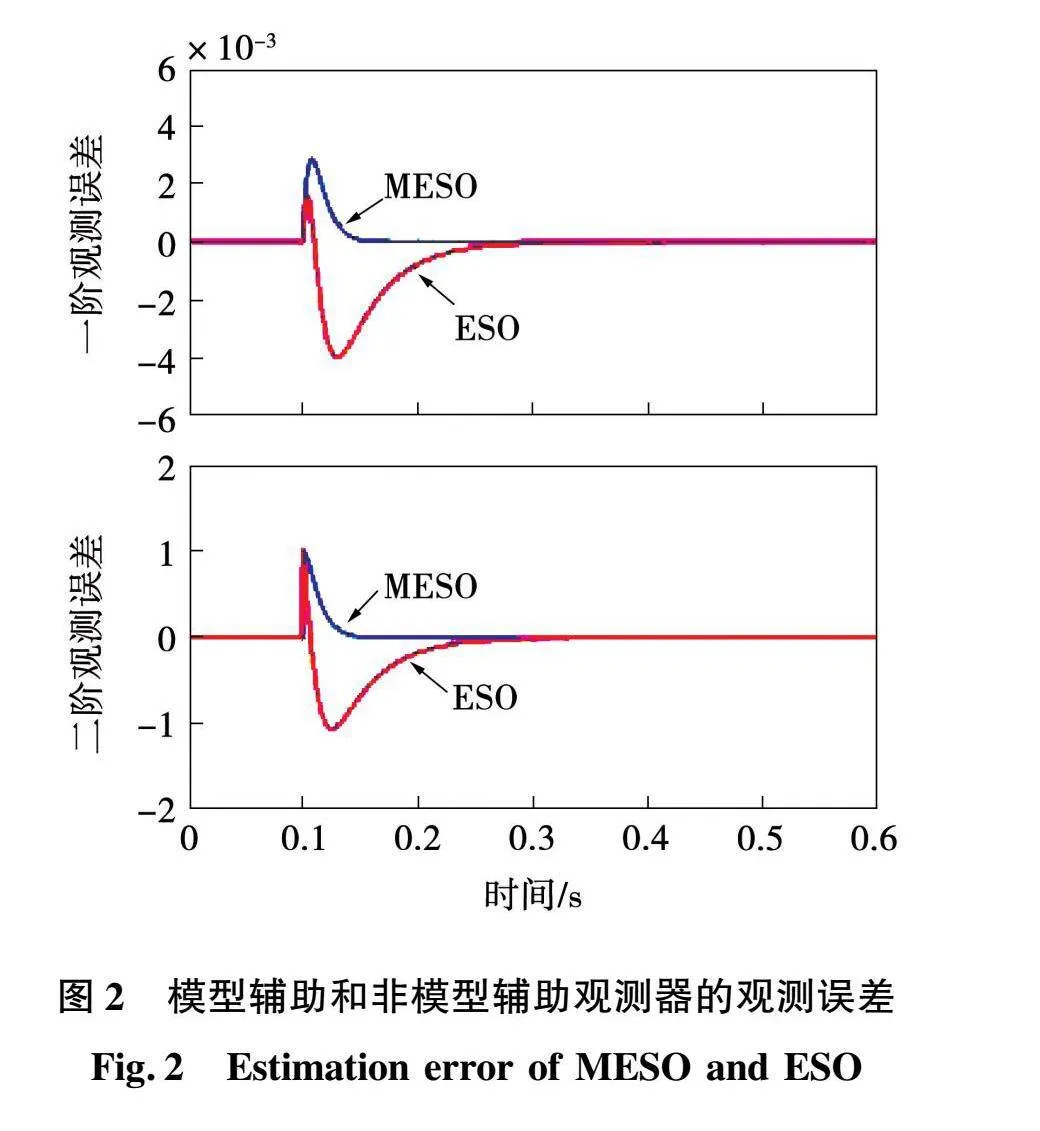
对于式（5）所示的状态观测器，各阶观测误差均可以快速衰减至零，且对单位阶跃扰动的观测误差的最大值分别为0.368/ωo和1。设t=0时刻系统受到单位幅值的阶跃扰动，扩张状态观测器对系统状态和扰动的观测误差如图2所示。

可以看出，MESO能在瞬态过程中较为准确地观测系统状态并估计扰动，表明MESO具有良好的动态观测能力。但在初始时刻，扩张状态即扰动的观测误差较大，即线性状态观测器存在微分峰值现象^[16]。此外，对比不含被控对象已知信息的扩张状态观测器，当取相同的增益系数时，MESO的观测误差更小，动态性能更优。

1.3 一阶LADRC系统的简化数学模型

根据式（5）和式（6），经拉普拉斯变换可得一阶自抗扰控制器的输出方程为：

u=1b0C（kpv－Hy）;（9）

C（s）=s2+（a+h1）s+h2s2+（h1+kp）s；

H（s）=（kph1－ah1+h2）s+kph2s2+（a+h1）s+h2。（10）

式中C（s）和H（s）分别为前向通道和反馈通道的传递函数。

令G（s）描述一阶被控对象，即

G（s）=1s+a。（11）

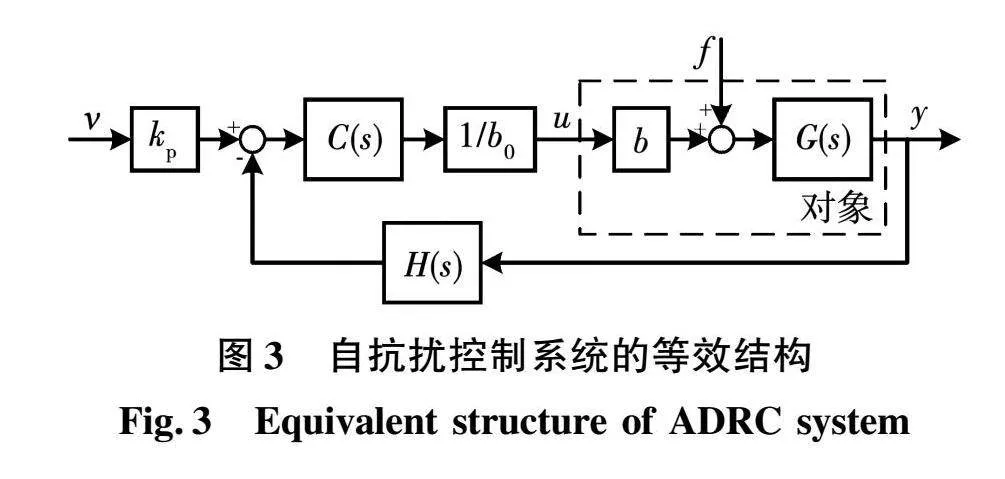
则上述一阶自抗扰控制系统可以等效为图3所示的系统。在该简化结构的系统中，扩张状态观测器和误差反馈控制律的作用仅由一个单闭环反馈回路表示。

由上述简化结构可求控制系统的输出方程和闭环传递函数为：

y=Gclv+Gyff;（12）

Gcl=kpCGbb01+CGHbb0N1（s）D（s）;（13）

Gyf=G1+CGHbb0N2（s）D（s）。（14）

式中：N1=［s2+（h1+a）s+h2］kpbb0；

N2=s2+（h1+kp）s；

D=s3+（h1+a+kp）s2+（kph1－ah1+h2）bb0s+

a（h1+kp）s+kph2bb0。

2 LADRC系统性能的参数化分析

由式（12）～式（14）可知，若对象参数a已知，控制系统的性能将由参数h1、h2、kp和b0共同决定。通过采用LADRC的带宽配置方法，即h1=ωo-a、h2=ω²o，kp在数值上等于控制器带宽，则上述参数被赋予了实际的物理意义，从而简化了控制系统性能的参数化分析过程。而控制补偿增益b0的取值为对b的估计值，此时控制系统的性能将完全取决于观测器带宽和控制器带宽。

2.1 系统稳定性分析

由图3可求控制系统的开环传递函数为

Gl=K0（T1s+1）s（T2s+1）（T3s+1）。（15）

式中：K0=Kbk2pω2oa（2ωo－a+kp）为开环传递函数的低频增益，Kb=b/b0为控制补偿比；

系数T1=（kp－a）（2ωo－a）+ω2okpω2o；

T2=1a；T3=1（2ωo－a+kp）。

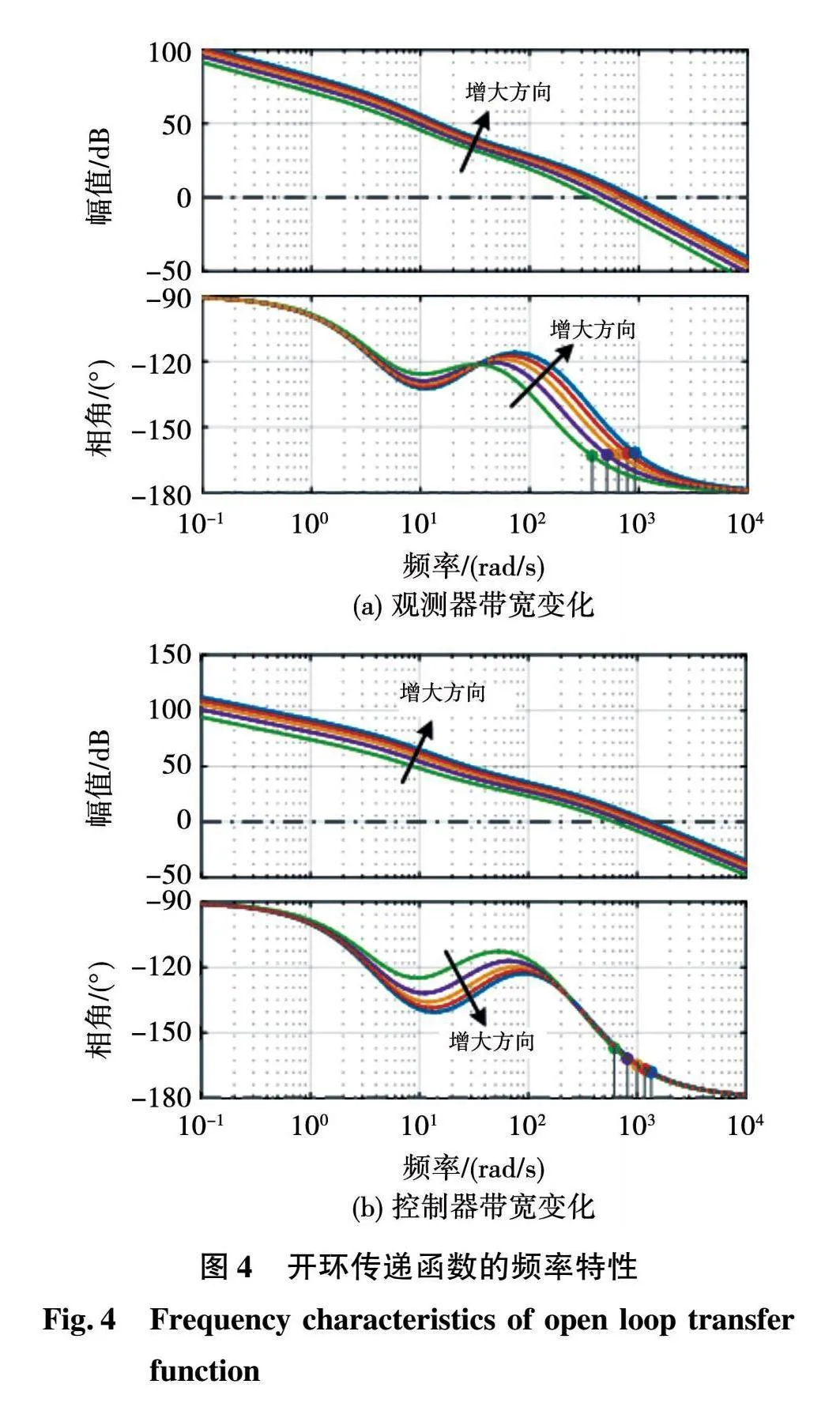
对于电机转速控制系统，由于存在机械转动惯量，控制系统式（12）的开环零、极点一般为负数，系统为最小相位系统。当观测器带宽和控制器带宽取不同值时，首先假设Kb=1，则系统开环传递函数的频率特性如图4所示。当带宽参数变化，系统的剪切频率随之改变，相频特性在中频段出现明显转折且最终趋于唯一的最小值-180°。因此根据Nyquist稳定性判据，闭环系统对于任意带宽参数均稳定。

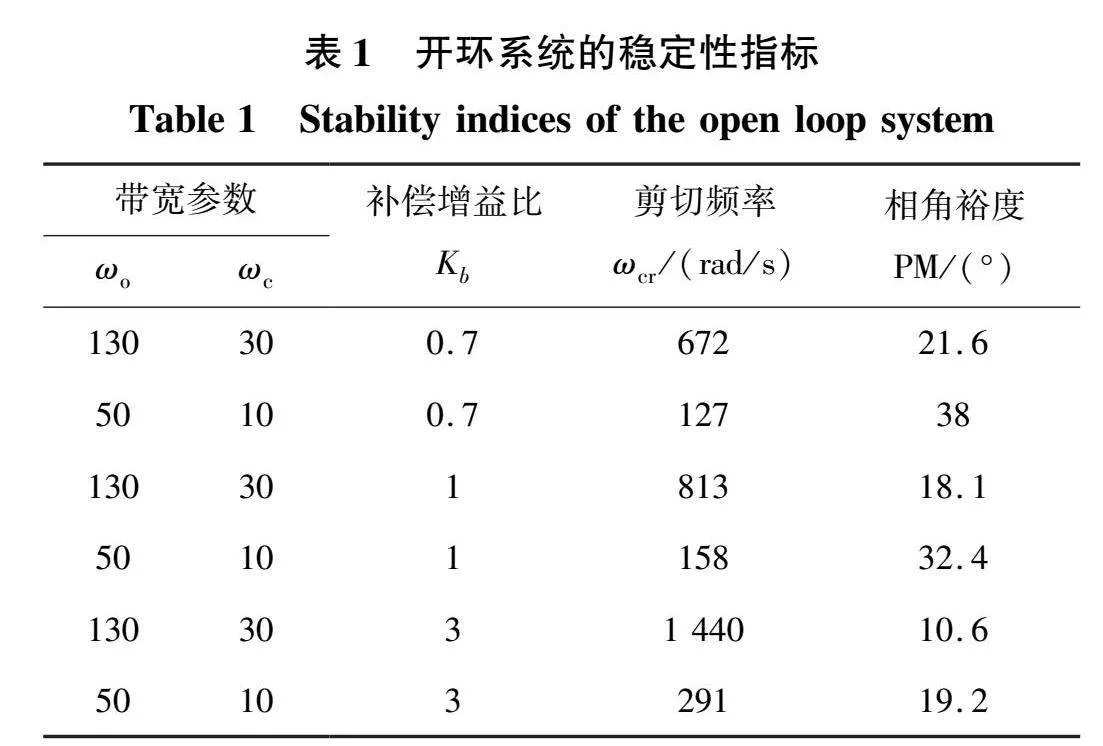
此外，由于Kb直接影响系统的低频开环增益而改变系统零、极点的分布，Kb≠1时控制系统的稳定性不变，但稳定裕度会有所不同。表1计算了带宽参数和Kb取不同值时开环系统的剪切频率和相角裕度，其中观测器带宽按工程经验取为控制器带宽的3～5倍^[4]。计算结果表明，当控制补偿增益b0较小即Kb较大时，系统的稳定裕度变小，因此b0的取值应满足控制系统对稳定裕度的要求。

2.2 系统跟随特性分析

b0为描述控制器补偿作用强弱的增益系数，一般取b0=b即Kb=1。忽略扰动f考察系统输出跟随期望给定的特性，则由式（13）可得，闭环系统的输出y关于输入v的传递函数可简化为一个一阶惯性环节，即

Gv=kps+kp。（16）

可见闭环系统的跟随性能仅和控制器带宽有关，进一步可求系统的阶跃响应为

y（t）=V（1－e^－kpt）。（17）

式中V为阶跃给定的幅值。

由式（17）可知，控制器带宽越大，自抗扰控制系统的跟踪速度越快，跟随性能也越好。用单位阶跃响应的调整时间ts1描述控制系统的跟踪速度，则ts1=3/kp。

2.3 系统抗干扰能力分析

扰动对控制系统输出的影响由扰动传递函数描述，将Kb=1代入式（14）可得系统输出关于扰动的传递函数为

Gf=s（s+2ωo+kp－a）（s+kp）（s+ωo）2。（18）

对于模型辅助ADRC系统，总扰动f既包含了未知的外部扰动，也包含了控制对象参数估计不准确或时变而导致的内部扰动。对于电机转速控制系统来说，外部扰动主要包括变化的机械负载以及电机转矩脉动。

1）负载变化扰动。

一般地，可将负载的突增或突卸看作一个阶跃变化形式的扰动。设t=0时刻控制系统受到一个阶跃变化的扰动f，其幅值为ΔTL，易得该扰动引起的系统输出为

y（t）=ΔTL［A1e^－kpt+（A2+A3t）e^－ωot］。（19）

式中：系数A1=－A2=2ωo－a（kp－ωo）2； A3=kp+ωo－akp－ωo。

特别地，若取ωo=kp=ω1，可求得式（19）的输出峰值Mp1≈0.736ΔTL/ω1，因此带宽参数越大，阶跃变化扰动对控制系统的影响就越小。

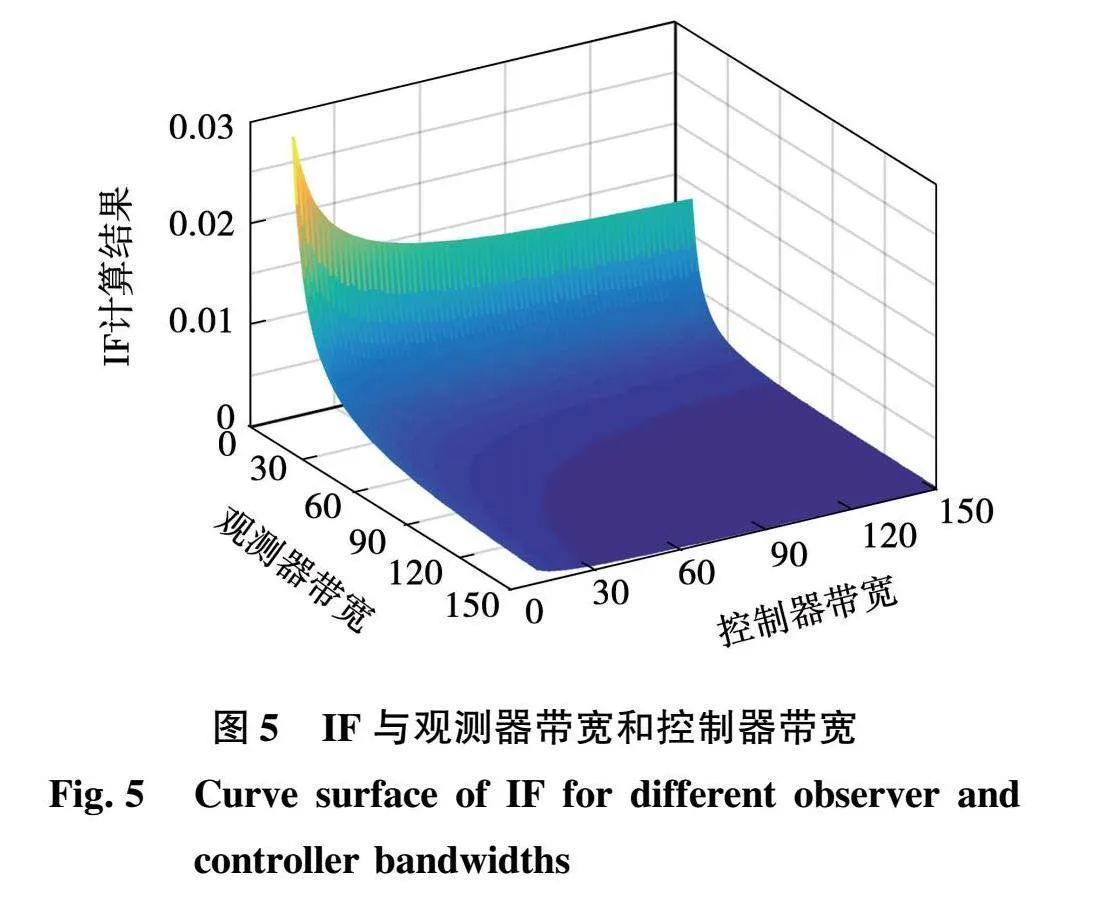
对于观测器和控制器带宽取值不相等的情况，定义IF为系统阶跃扰动响应的绝对值积分，即

IF=∫∞0|y（t）|dt=ΔTL（2ωo+kp－a）kpω2o。（20）

IF的大小描述了控制系统对阶跃变化扰动的抑制效果，且IF越小说明系统阶跃响应的幅值变化越小，恢复时间越短，即控制系统对扰动的抑制能力越强。图5绘制了IF关于带宽参数变化的曲面，可见当观测器带宽和控制器带宽取值较大时，系统的抗干扰能力得到了明显增强。

2）转矩脉动扰动。

对于电机转速控制系统来说，系统的控制量即转矩为光滑的平均转矩，然而在实际的控制系统中，尤其在开关磁阻电机的转速-转矩双闭环控制系统中，转矩脉动不可忽略，是控制系统的另一种主要干扰源。

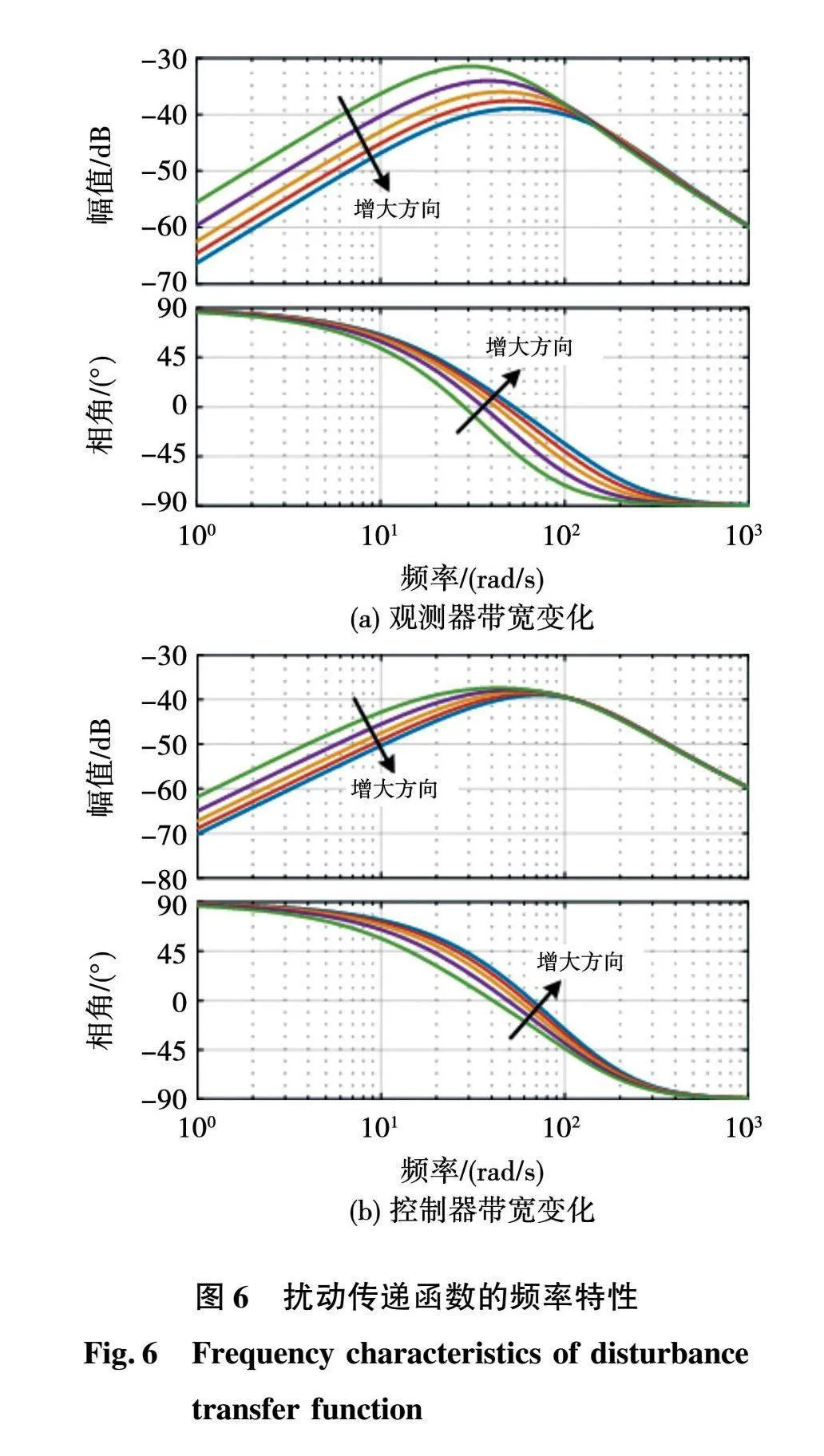
转矩脉动按照机理可分为由开关器件斩波导致的高频转矩脉动和由电机结构以及换相导致的中、低频转矩脉动。图6绘制了扰动传递函数的频率特性曲线。可以看出，扰动传递函数的幅频特性在全频段范围内均为负数，说明自抗扰控制系统对不同频率的扰动均有抑制效果，并且当观测器带宽和控制器带宽较大时，系统对扰动的抑制效果也更好。对于电机控制系统来说，开关频率一般不低于15 kHz，即由斩波导致的转矩脉动的频率约在10⁵ rad/s以上。而电机固有转矩脉动的频率和电机的结构以及转速相关，一般在10³ rad/s以上，因此上述扰动的影响均可以得到有效的抑制。

总的来说，自抗扰控制器的带宽参数主要影响控制系统对中、低频扰动的抑制效果，且系统的抗干扰能力在谐振频率处最差，Gf的谐振峰为

L（ωr1）≈20lg2ωo+kp－a2ω2o。（21）

2.4 系统噪声抑制能力分析

对于电机转速控制系统，由于传感器采样和数值运算等因素，闭环反馈的转速中往往叠加了噪声信号，噪声对控制系统输出的影响由传递函数Gδ描述。由图3所示的ADRC系统的等效结构，可求得Kb=1时噪声传递函数为

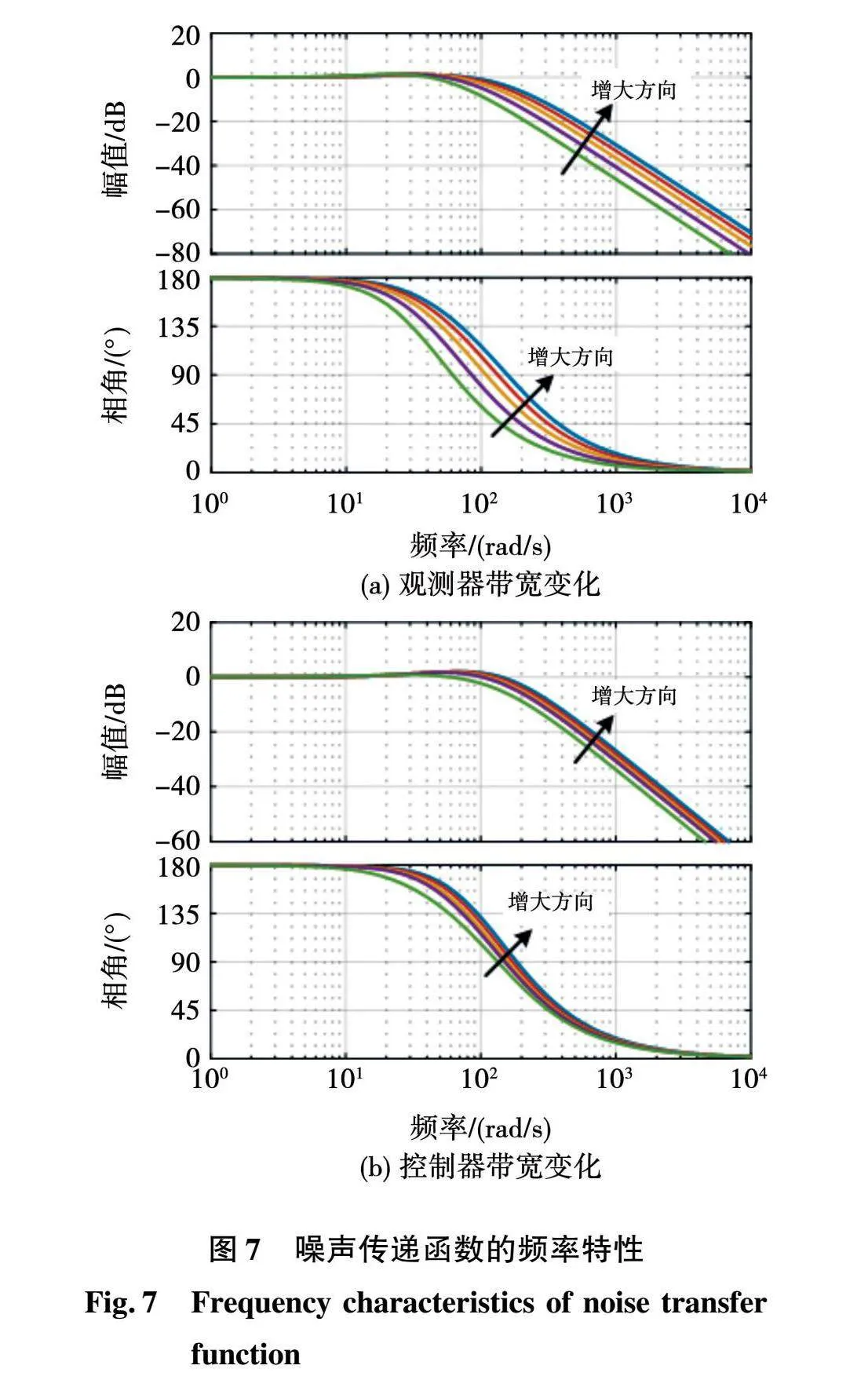
Gδ=－［（kp－a）（2ωo－a）+ω2o］s－kpω2o（s+kp）（s+ωo）2。（22）

噪声传递函数的频率特性如图7所示，在高频段幅频特性的斜率约为-40 dB/dec，说明控制系统对输出侧的高频噪声具有抑制作用，且抑制效果主要取决于观测器带宽ωo。观测器带宽越大，系统对高频噪声的抑制能力越弱。而在中、低频，系统的截止频率ωb1≈ωo，且对于低于截止频率的噪声不具有抑制能力。

2.5 系统参数鲁棒性分析

上文基于被控对象模型已知或近似已知的情况建立了模型辅助自抗扰控制器，这与实际应用相吻合。但当模型参数估计不准确或随时间变化时，系统性能的受影响程度反映了系统的鲁棒性。

抗干扰能力强是ADRC系统的主要优势之一，其关于对象参数的灵敏度为

Sa=Gf（s）aaGf（s）=－as（s+ωo）2。（23）

灵敏度越小，扰动传递函数对模型参数a的变化越不敏感，控制系统关于模型参数a的鲁棒性也就越好。

由上式可求扰动传递函数的最大灵敏度为

‖Sa‖∞=maxω－aωj（ωo+ωj）2=a2ωo。（24）

可见系统的鲁棒性只取决于观测器带宽，且观测器带宽越大，系统关于被控对象参数的鲁棒性越强。总的来说，ADRC系统对被控对象参数不敏感，当对象参数在较大范围内变化时，系统的输出性能近似不变。

3 参数快速整定方法与对比分析

3.1 基于系统性能优化的参数快速整定方法

通过将控制器的增益配置为仅和带宽有关的参数，LADRC系统的待整定参数仅为一个观测器带宽和一个控制器带宽，且两种带宽参数和系统性能紧密相关。总的来说，较大的控制器带宽可以提高系统的动态响应性能，但过大也会降低系统的稳定性和效率。与此同时，观测器带宽直接影响系统状态和扰动的观测误差，足够的观测器带宽是提高控制系统抗干扰能力和鲁棒性的重要因素，但也会引入更多噪声。因此在进行控制器参数整定时，必须综合考虑两种参数对系统多方面性能的影响。

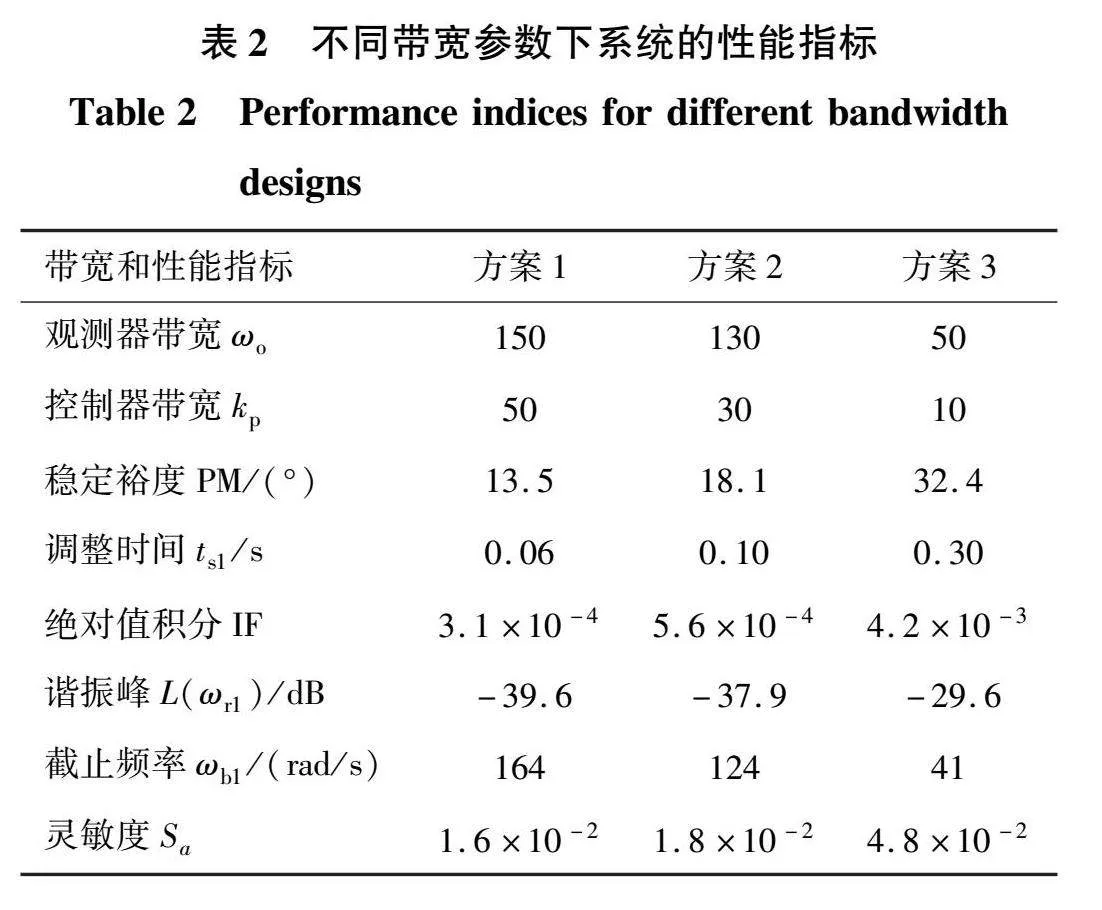
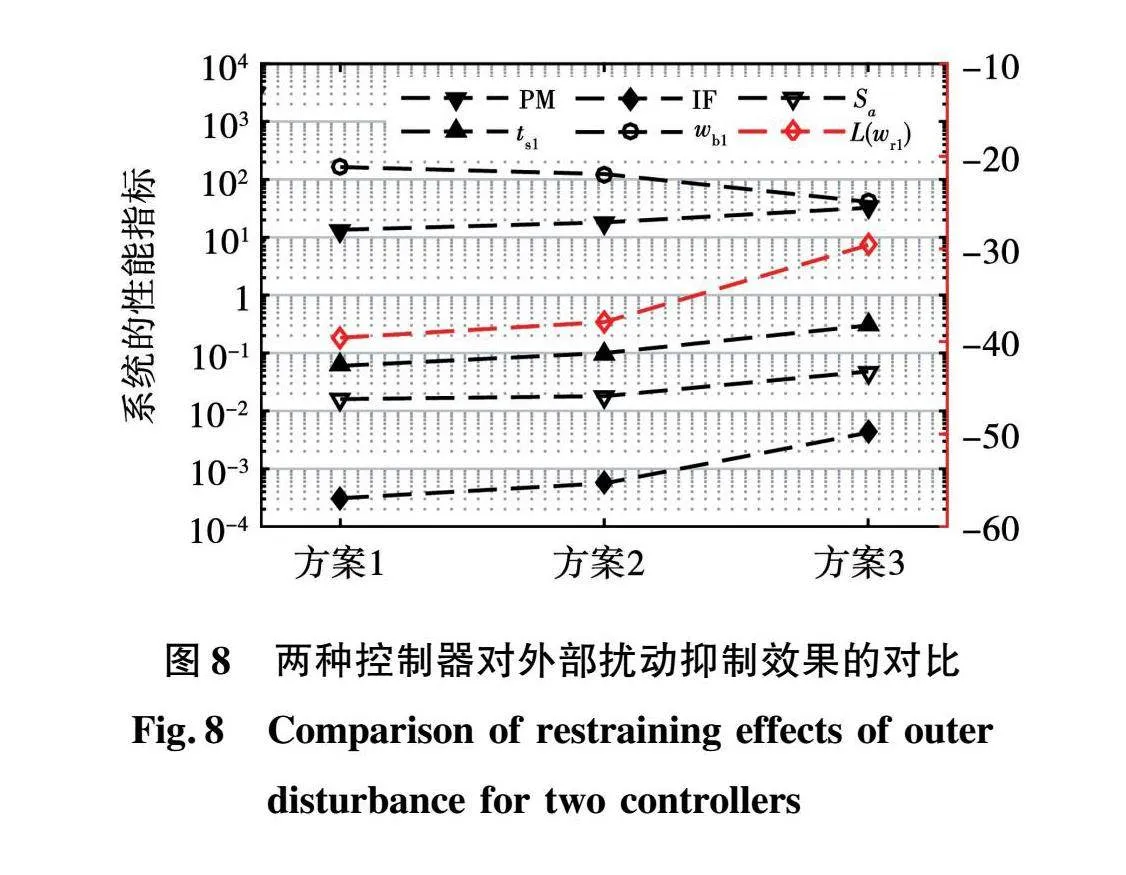
根据上文得到的LADRC系统性能参数化分析结果，可以快速设计满足不同性能需求的控制器参数。首先设计两个带宽参数在较大范围内变化，控制系统将呈现明显不同的性能，从而快速确定带宽参数的合适范围。在此基础上，通过对两个带宽参数分别进行微调，可以针对性地改善系统的某一个或几个控制性能，最终控制器的参数整定结果如表2和图8所示，其中谐振峰L（ωr1）绘制在右坐标系中。本文折中选择方案2并进行后续验证。

上述方法实现了自抗扰控制器带宽参数的快速整定，而控制补偿增益b0的值一般取为对模型参数b的估计值，当系统的实际输出存在振荡或较大时滞时，可进一步微调b0的值至最优。总的来说，b0较大时系统的稳定裕度更高，稳定性更好。

3.2 与传统PI控制的对比分析

对于开关磁阻电机转速控制，可以采用一个一阶PI控制器，配置PI控制器的参数使系统输出式（16）所示的跟随特性，则PI控制器的比例和积分系数满足：

Kp=kp/b；KI=akp/b。（25）

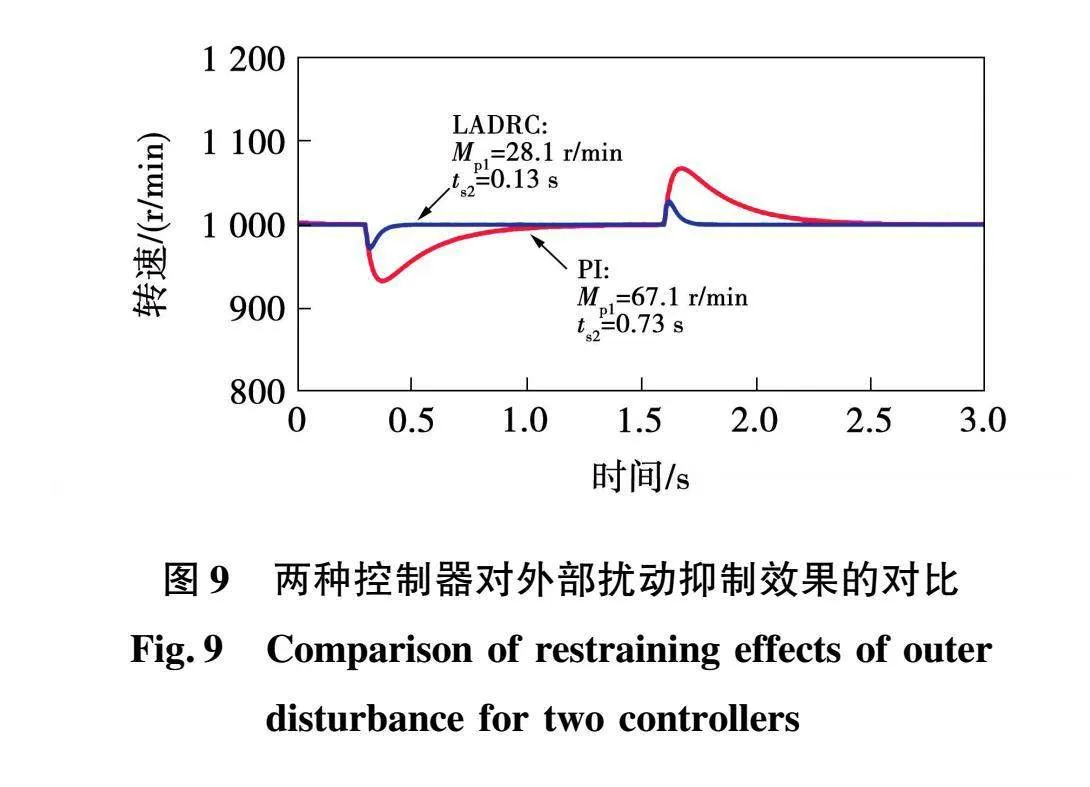
将线性自抗扰控制器和PI控制器分别应用于开关磁阻电机的转速闭环控制，并取控制器的带宽参数ωo=130、kp=30，仿真结果与对比如图9所示。可以看出，当两种控制系统输出相同的跟随特性时，线性自抗扰控制器对扰动的抑制效果更优，电机的转速波动更小、恢复更快。

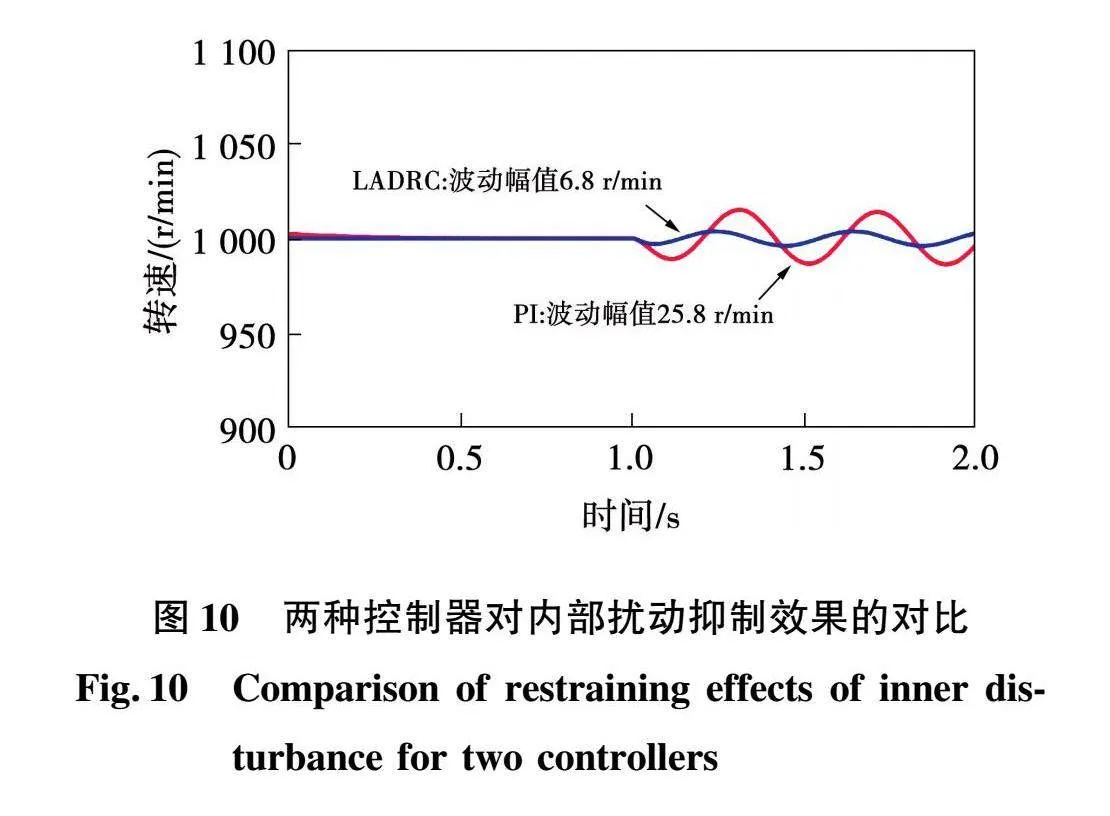
当电机参数发生变化时，两种控制器的输出特性也不同。令系统达到稳态后t=1 s时刻电机的阻尼系数上下波动20%，仿真结果如图10所示。可见两个控制系统均能输出较为平稳的转速，转速波动分别为6.8 r/min和25.8 r/min，因此自抗扰控制器的参数鲁棒性更高。

4 SRM转速控制系统实验验证

开关磁阻电机结构简单且易于控制，但具有较强的非线性特性，因此较难建立其精确的模型。本文以370 W四相8/6极开关磁阻电机为控制对象，利用线性自抗扰控制器实现其转速控制，并对自抗扰控制器的性能和对象参数鲁棒性进行验证。搭建的实验平台如图11所示，由开关磁阻电机、直流负载、传感器和驱动控制系统组成。其中开关磁阻电机的转动惯量约为0.008 22 kg·m²，阻尼系数约为0.001 72 N·m·s/rad，由此计算得到的控制对象系数如图11所示。增量式光电编码器用于测量电机转子位置信息，霍尔电流传感器用于采样绕组的电流。控制系统的DSP选用TMS320F28335，并通过上位机实时监控电机的转速和转矩。

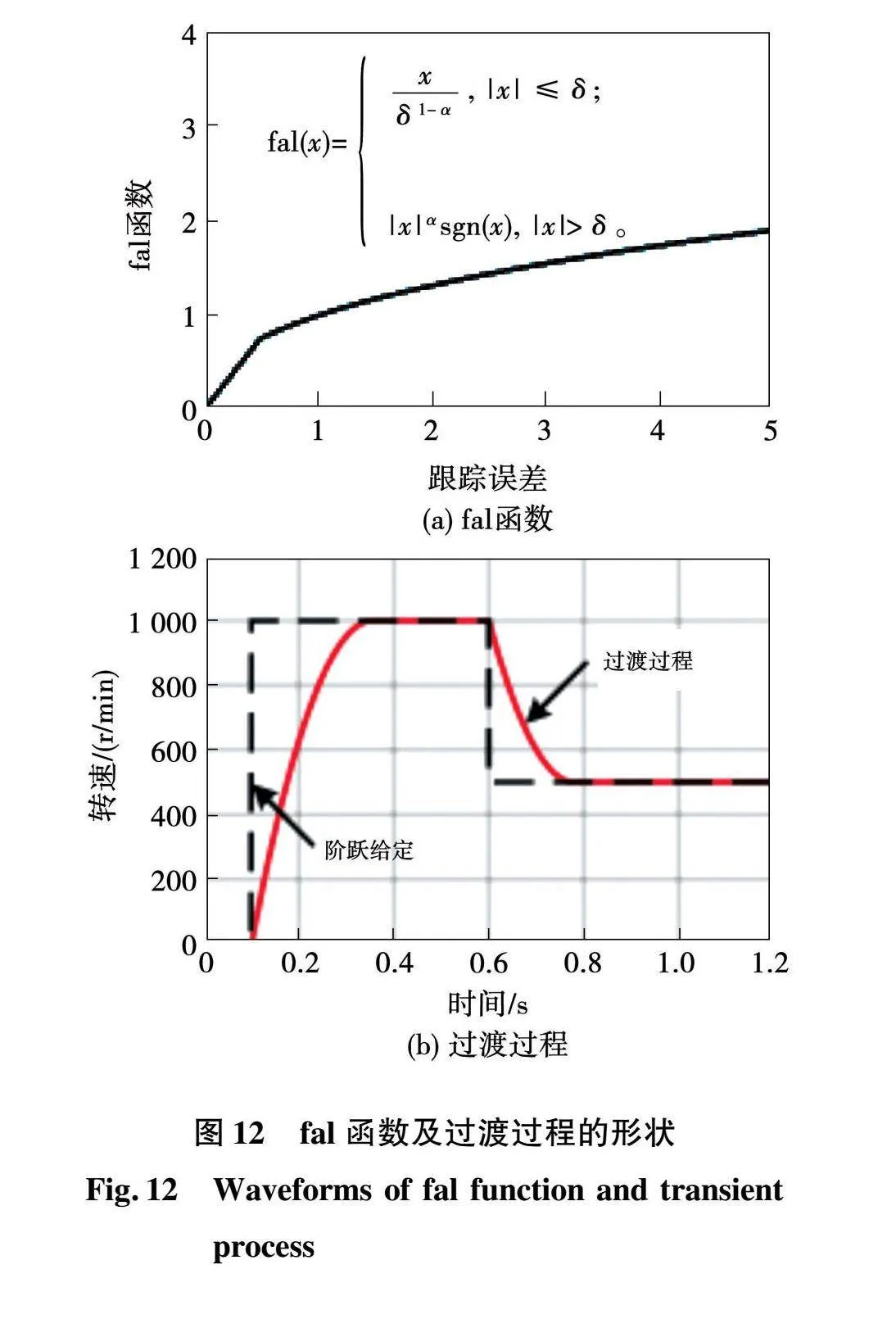
为了获得更好的动态性能，本文利用fal函数对转速给定设计了如下过渡过程，fal函数的形状及过渡过程如图12所示。过渡过程表达式为

v·1=rfal（v－v1）。（26）

式中：v1为过渡过程的输出；r为描述跟踪速度的系数。

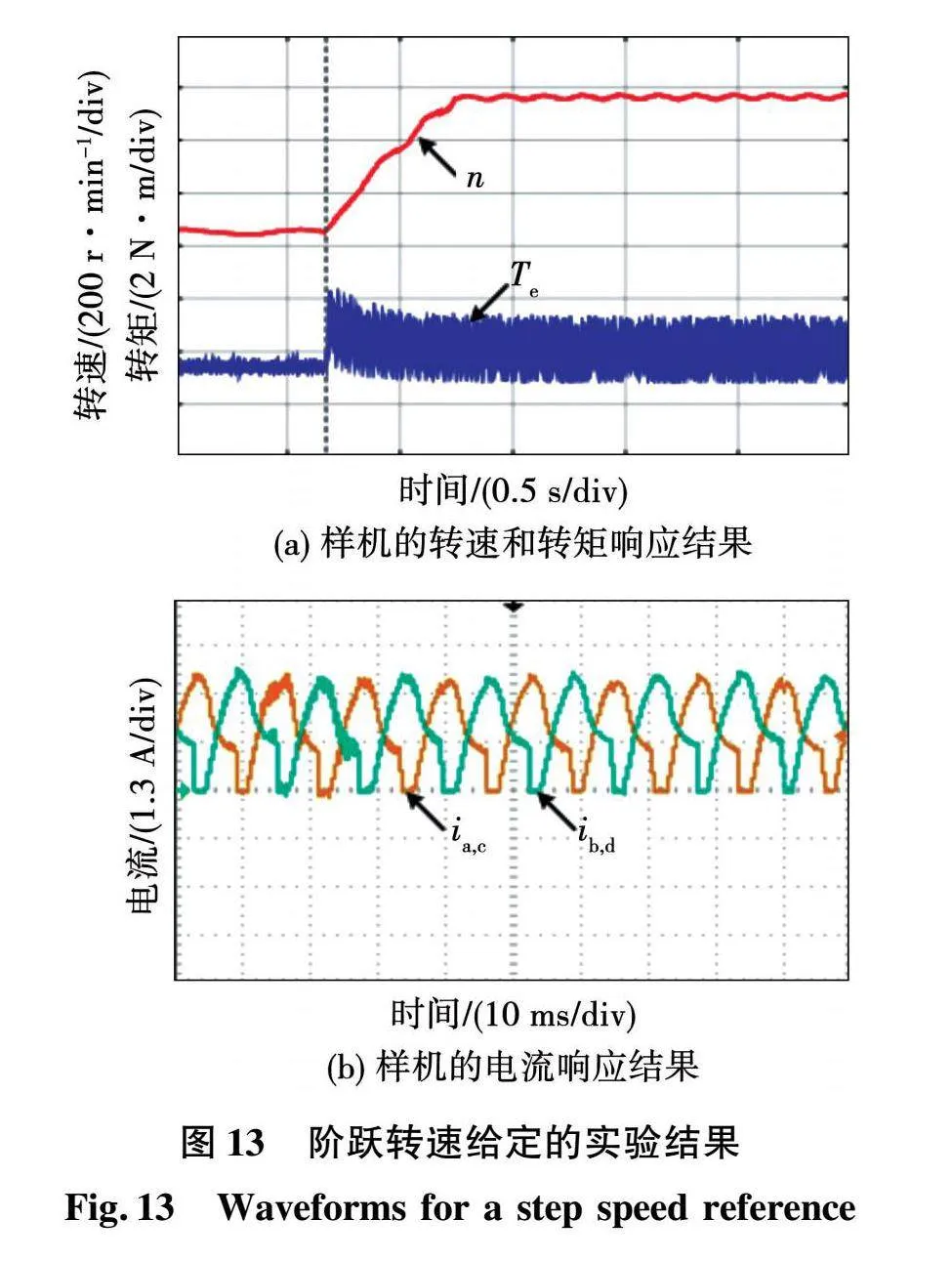
起动时设定转速的参考值突变600 r/min，通过上位机观察转矩-转速传感器的输出信号，结果如图13所示。电机转速可以快速跟随给定的转速值，上升时间约为0.5 s且动态过程中没有明显振荡，稳态后转速响应几乎没有静差且脉动较小，说明控制器具有较好的跟随性能和参数鲁棒性。稳态下测得的相电流波形如下，其中四相开关磁阻电机采用相邻两相同时导通的工作方式，即A、C相和B、D相不会同时导通，因此通常采用共用上桥臂的驱动电路。图中相电流波形为共用桥臂中的电流。

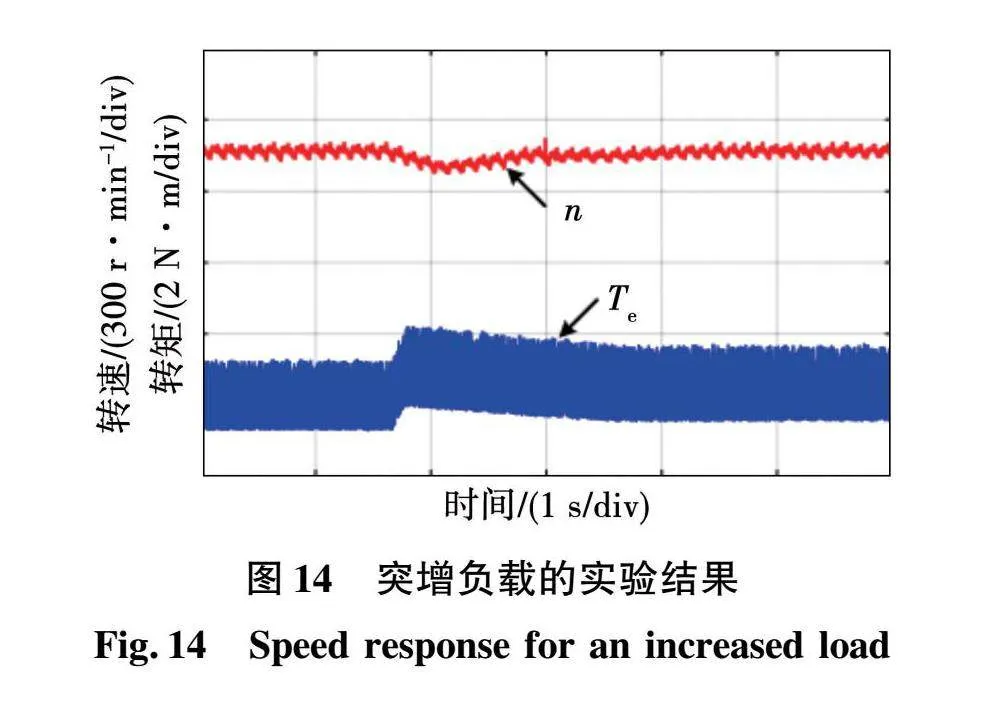
图14为负载突然增大时的实验结果，通过调节直流负载的电枢绕组使负载转矩增大0.5 N·m时，转速出现跌落，最大值约12%，并在约1 s后趋于平稳。输出速度总体上保持稳定，表明系统具有较强的抗干扰能力。

5 结 论

本文以一阶模型辅助线性自抗扰控制器为研究对象，提出一种控制器参数的快速整定方法，并将其应用于开关磁阻电机自抗扰转速控制系统中。结论如下：

1） 通过研究LADRC参数对系统性能的影响规律，实现了基于系统性能指标的控制器参数快速设计，有效简化了复杂的控制器参数整定过程。

2） 仿真和实验结果证明，采用所提出方法设计的LADRC系统具有较好的抗干扰能力和参数鲁棒性。

本文的研究成果有助于促进线性自抗扰控制在电机转速控制或其他领域的工程应用。

参 考 文 献：

［1］ HAN Jingqing. From PID to active disturbance rejection control [J]. IEEE Transactions on Industrial Electronics， 2009， 56（3）： 900.

［2］ ZHANG Chaoyu， ZHANG Chengming， LI Liyi， et al. An enhanced nonlinear ADRC speed control method for electric propulsion system： modeling， analysis， and validation [J]. IEEE Transactions on Power Electronics， 2023， 38（4）： 4520.

［3］ YUAN Changsheng， ZHOU Xuesong， MA Youjie. DC bus voltage control of wind power inverter based on first-order LADRC [J]. IEEE Access， 2022， 10： 3263.

［4］ GAO Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//American Control Conference， June 4-6， 2003， Denver， USA. 2003： 4989-4996.

［5］ FENG Liyun， SUN Xiaodong， TIAN Xiang， et al. Direct torque control with variable flux for an SRM based on hybrid optimization algorithm [J]. IEEE Transactions on Power Electronics， 2022， 37（6）： 6688.

［6］ DU Chao， YIN Zhonggang， ZHANG Yanping， et al. Research on active disturbance rejection control with parameter autotune mechanism for induction motors based on adaptive particle swarm optimization algorithm with dynamic inertia weight [J]. IEEE Transactions on Power Electronics， 2019， 34（3）： 2841.

［7］ WANG Gaolin， LIU Ran， ZHAO Nannan， et al. Enhanced linear ADRC strategy for HF pulse voltage signal injection-based sensorless IPMSM drives [J]. IEEE Transactions on Power Electronics， 2019， 34（1）： 514.

［8］ XUE W， HUANG Y. On frequency-domain analysis of ADRC for uncertain system[C]//American Control Conference， June 17-19， 2013， Washington， USA. 2013： 6637-6642.

［9］ JIN Huiyu， SONG Jingchao， ZENG Song， et al. Linear active disturbance rejection control tuning approach guarantees stability margin[C]//15th International Conference on Control， Automation， Robotics and Vision， November 18-21， 2018， Singapore. 2018： 1132-1136.

［10］ 张皎， 杨旭， 刘源翔， 等. 高阶线性自抗扰控制器的性能评估 [J]. 控制与决策， 2015， 30（7）： 1162.

ZHANG Jiao， YANG Xu， LIU Yuanxiang， et al. Performance evaluation for active disturbance rejection with high-order line extended state observer [J]. Control and Decision， 2015， 30（7）： 1162.

［11］ 张彬文， 谭文， 李健. 基于频域近似的线性自抗扰参数整定 [J]. 控制理论与应用， 2019， 36（5）： 831.

ZHANG Binwen， TAN Wen， LI Jian. Tuning of linear active disturbance rejection control via frequency domain approximation [J]. Control Theory amp; Applications， 2019， 36（5）： 831.

［12］ ZHANG Bin， YOU Shijun， LIU Mao， et al. Design and parameter tuning of nonlinear active disturbance rejection controller for permanent magnet direct drive wind power converter system [J]. IEEE Access， 2021， 9： 33839.

［13］ 刘勇智， 戴聪， 王程. 基于自抗扰的航空开关磁阻转速转矩控制方法 [J]. 电机与控制学报， 2020， 24（4）： 116.

LIU Yongzhi， DAI Cong， WANG Cheng. Method on aerial reluctance switched speed-torque control based on auto disturbances rejection [J]. Electric Machines and Control， 2020， 24（4）： 116.

［14］ JIN Huiyu， CHEN Yang， LAN Weiyao. Replacing PI control with first-order linear ADRC[C]//IEEE 8th Data Driven Control and Learning Systems Conference， May 24-27， 2019， Dali， China. 2019： 1097-1101.

［15］ ZHONG Sheng， HUANG Yi， GUO Lei. A parameter formula connecting PID and ADRC [J]. Science China （Information Sciences）， 2020， 63（9）： 175.

［16］ 孙佃升， 章跃进. 一种抑制初始微分峰值现象的改进型三阶时变参数扩张状态观测器 [J]. 电机与控制学报， 2017， 21（9）： 55.

SUN Diansheng， ZHANG Yuejin. Improved third-order time-varying parameters nonlinear ESO restraining the derivative peaking phenomenon [J]. Electric Machines and Control， 2017， 21（9）： 55.

（编辑：邱赫男）