一种准Z源逆变器驱动的六相永磁同步电动机转矩脉动抑制

摘 要：与三相永磁同步电动机（PMSM）相比，六相PMSM在抑制转矩脉动和故障容错等方面具有优势，适用于航空航天、国防等对可靠性有较高要求的领域。目前，六相PMSM系统大多使用的是电压源逆变器，特点是交流侧输出受限于电源电压，且逆变器中桥臂的死区会使输出电流发生畸变，使电动机产生转矩脉动。准Z源逆变器是一种集逆变和升压于一体的新型功率变换结构，且无需死区时间。将六相PMSM和准Z源逆变器结合在一起，提出一种新的空间矢量脉宽调制（SVPWM）策略，针对算法中有效矢量对q轴电流的变化进行补偿，并将直通时间插入到有效矢量之间，以抑制q轴电流脉动，从而减小转矩脉动，且该方法对零矢量的最大利用率可达100%。最后，通过仿真和实验验证了该PWM调制方式对转矩脉动抑制的有效性及可行性。

关键词：转矩脉动抑制；四矢量SVPWM；准Z源逆变器；升压；矢量作用时间；永磁同步电动机

DOI：10.15938/j.emc.2024.11.008

中图分类号：TM341

文献标志码：A

文章编号：1007-449X（2024）11-0081-13

Suppression of torque ripple in six phase PMSM driven by quasi Z-source inverter

GAO Hanying， SHU Tianhao， ZHAO Kangxu

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080，China）

Abstract：Compared with three-phase permanent magnet synchronous motor （PMSM）， six-phase PMSM have advantages in suppressing torque ripple and fault tolerance， and are suitable for aerospace， national defence and other occasions that require high reliability. In six-phase PMSM systems， voltage source inverters were predominantly employed， with the AC-side output being constrained by the supply voltage， and the dead zone of the bridge arms in the inverter causing output current distortion， causing torque ripple in the PMSM. Quasi Z-source inverter is a new power conversion structure that combines both inverter and boost functions and does not require dead time. A new space vector pulse width modulation （SVPWM） strategy was proposed by combining six-phase PMSM and quasi Z-source inverter. The change of q-axis current was compensated by the effective vector in the algorithm， and the shoot-through time was inserted between the effective vectors to suppress the q-axis current ripple and reduce the torque ripple and the method can achieve a maximum utilization of up to 100% for zero vector. Finally， effectiveness and feasibility of this PWM method for torque ripple suppression were verified by simulation and experiment.

Keywords： torque ripple suppression; four-vector SVPWM; quasi-Z-source inverter; boost; vector action time; permanent magnet synchronous motor

0 引 言

现有的永磁同步电动机（permanent magnet synchronous motor，PMSM）驱动系统通常采用的是电压源逆变器，交流侧输出电压不能高于直流侧电源^[1]；同时，为了确保系统的安全可靠性，电压源逆变器（voltage source inverters，VSI）同一桥臂中需引入死区时间，从而使VSI输出相电流发生畸变，产生转矩脉动^[2]。

针对VSI存在的问题，文献[]提出一种Z源逆变器（Z-source inverter，ZSI），即由无源器件组成的对称阻抗源网络，连接直流电源和逆变器，具有允许桥臂直通、调压范围宽、电流输出畸变小等优点，但是，它的电容电压应力较高，并且输入电流是断续的。文献[4]提出一种改进型准Z源逆变器（quasi-Z-source inverter，QZSI），该种结构不仅可以达到升压的目的，还可以降低启动电流和电容电压应力。QZSI和ZSI具有相同的电压增益，升压能力不足，因此难以满足某些高压场合的需求。

针对这一问题，国内外研究人员一直在不断地改进ZSI的拓扑，以寻求更高的电压增益。文献[5]提出一种准Z源间接矩阵变换器拓扑结构，这种拓扑结构比传统的两种拓扑结构输出电压增益高。为了使阻抗源网络输出更高的电压，文献[6]提出一种基于耦合电感的QZSI，该拓扑不仅具有ZSI的优势，同时利用耦合电感，使得QZSI因耦合电感的存在，能够通过改变电感的匝数和逆变器的占空比这两个自由度来调节阻抗源网络的输出电压，通过调整电感的匝数就能够在较小的占空比下让阻抗源网络的输出电压进一步提高。文献[7]提出一种倍压型ZSI，这种拓扑结构能够对漏感能量再利用，可以减小由于开关电感的引入产生的直流链电压尖峰。

在PMSM电机驱动领域，ZSI的成本低、结构简单且可靠性高，具有广泛的应用前景。因此，针对PMSM和ZSI相结合的控制策略被相继提出。文献[8]将ZSI应用于三相永磁同步电机驱动系统中，充分利用ZSI的升压特性，扩大了电动机的调速范围。ZSI应用于电机驱动系统的优势不仅体现在升压能力上，还在于可调的直流链电压，这是一个额外的能够影响驱动系统性能的自由度。文献[9]提出一种改进自抗扰控制的直流链电压控制技术。此外，文献[10]将滑模控制和前馈补偿相结合，在基于Z源逆变器的PMSM驱动系统中得到应用。文献[11]提出一种串联虚拟阻抗的形式来抑制电感的纹波电流，提高了系统的运行稳定性。

与三相PMSM相比，六相PMSM具有转矩脉动幅值小、相电流谐波成分低及容错能力高等优点。文献[12]介绍了应用六相Z源逆变器的简单升压（simple boost，SB）和最大升压（maximum boost，MB）调制方式，并提出一种减小开关损耗的调制方法。然而，SB调制方式升压比较低，MB调制方式的直通时间是变化的，这对无源元件提出了更高的要求。文献[1]提出一种应用于六相ZSI的改进最大恒定升压（maximum constant boost，MCB）调制方法，相较于SB方法，MCB具有更高的升压比；与MB方式相比，MCB具有恒定的直通时间，需要更少的Z源网络无源元件。与正弦脉宽调制技术相比，空间矢量脉宽调制（space vector pulse width modulation，SVPWM）技术数字化更易于实现。文献[14]提出一种基于神经网络分类的Z源六相逆变器SVPWM控制策略，由于神经网络算法的引入，增加了计算难度，难以实际应用。

以QZSI和六相PMSM驱动系统构成的系统为研究对象，构建一个可调直流母线电压和桥臂无死区的驱动系统，即在QZSI和四矢量SVPWM的基础上，提出一种新的SVPWM调制策略，采用非平均直通分段方式实现升压，以抑制转矩脉动，最后通过在MATLAB中进行仿真及实验对所提出调制策略和系统性能进行验证。

1 准Z源逆变器工作原理

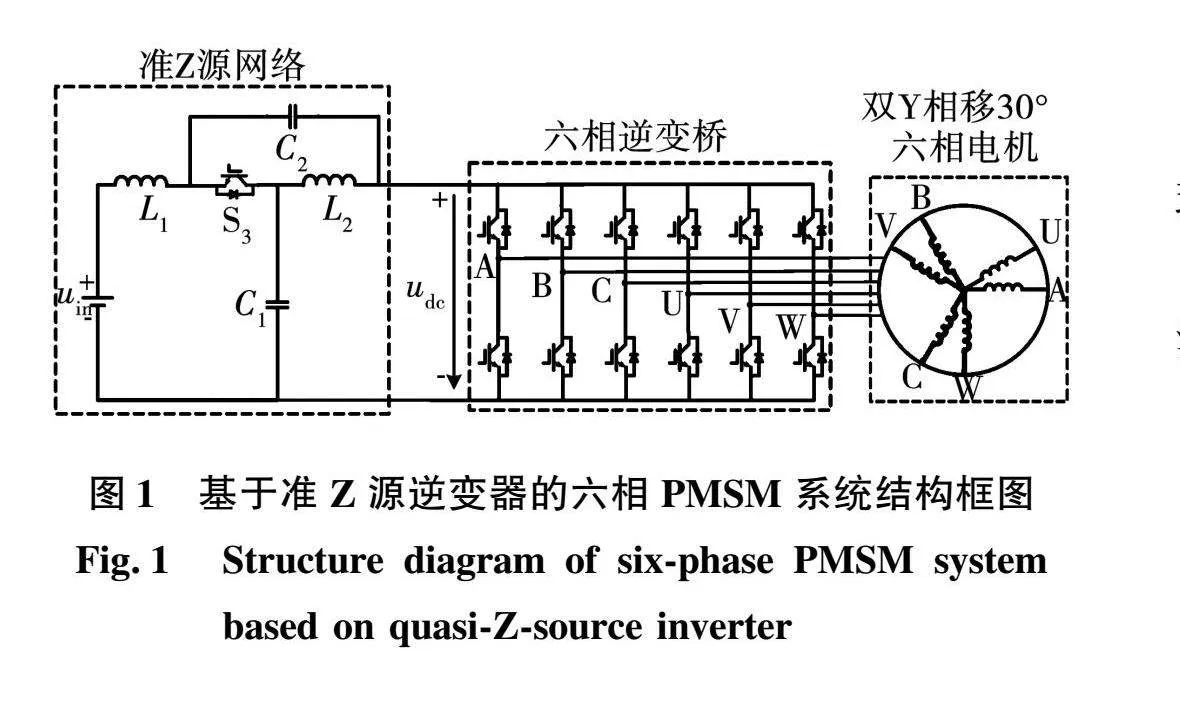
图1为基于准Z源逆变器的六相PMSM系统结构框图，由准Z源网络、六相逆变桥及六相永磁同步电机构成。由于准Z源网络的存在，一个半桥的两个功率开关管可同时导通，即直通。正是有直通状态的存在，才使得准Z源网络具有升压能力。

为了便于分析，假定Z源网络中无源器件的取值相同，即L1=L2=L，C1=C2=C。

图2展示了QZSI中逆变器处于直通和非直通两种工作状态下工作时的等效电路。无源器件电压、电流的正方向如图2（a）所示。

如图2（a）所示，当QZSI工作在直通状态时，电容C1对电感L2进行充电，直流电压源uin以及电容C2同时对电感L1进行充电，由基尔霍夫电压定律得出：

uin=uL1－uC2；

uL2=uC1；

udc=0。（1）

如图2（b）所示，当QZSI工作在非直通状态时，电感L1、L2和直流稳压电源放电，电容C1、C2充电，由基尔霍夫电压定律得出：

uin=uC1－uL1；

udc=uC1－uL2；

uL2=uC2；

udc=uC1+uC2。（2）

将开关周期设为Ts，直通时间设为Tsh，对电感L1、L2两端电压采用伏秒平衡原理分析，可得到：

uL1=Tsh（uin+uC2）+（Ts－Tsh）（uin－uC1）Ts=0；

uL2=TshuC1－（Ts－Tsh）uC2Ts=0。（3）

对式（3）整理后可得：

（uin+uC2）Dsh=（1－Dsh）（－uin+uC1）；

uC1Dsh=（1－Dsh）uC2。（4）

式中Dsh为直通占空比，Dsh=Tsh/Ts。

对式（4）化简整理后可以得到uC1、uC2和输入直流母线电压uin之间的关系式为：

uC1=1－Dsh1－2Dshuin；

uC2=Dsh1－2Dshuin。（5）

结合式（2）和式（5）可以得出，在非直通状态下直流链电压值udc与电容电压uC1、uC2和直流母线电压uin之间的关系为

udc=uC1+uC2=11－2Dshuin=Buin。（6）

式中升压因子B=1/（1－2Dsh），它通过直通占空比计算得出，表示准Z源网络的升压能力。

2 六相永磁同步电机数学模型

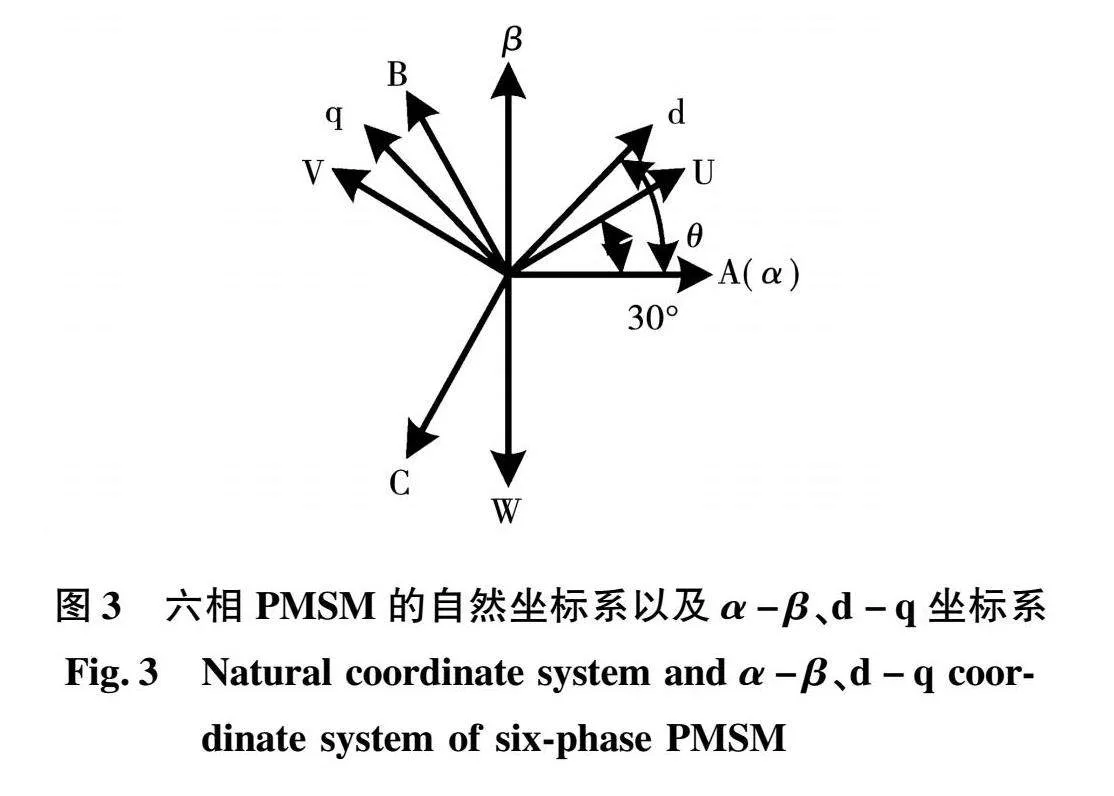
以图1所示的非对称六相PMSM为对象，它包括ABC和UVW两套绕组，在这两套绕组中各相均相差120°，A相和U相的电角度相差30°。六相电机在磁势空间分布上与十二相电机类似，转矩脉动频率上升至12次，转矩脉动幅度变小。图3为六相 PMSM 两套绕组的变量在α-β与d-q坐标系间的关系。

将六相PMSM进行矢量空间解耦变换，其各种变量映射在3个相互垂直的α-β、Z1-Z2与O1-O2平面。与α-β平面对应的变量与能量变换有关，与 Z1-Z2、O1-O2平面对应的变量与能量变换无关。

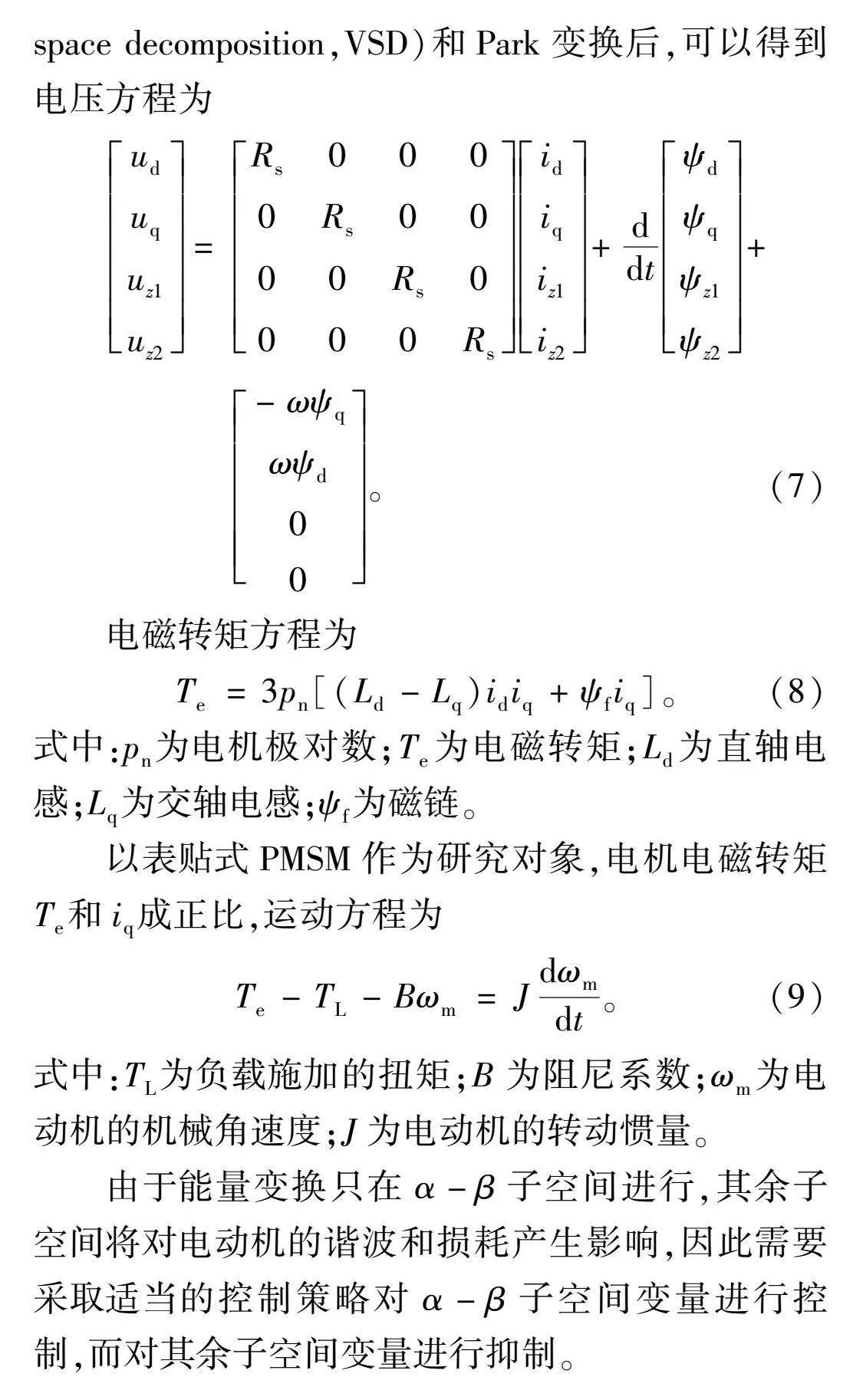
六相PMSM经过矢量空间解耦变换（vector space decomposition，VSD）和Park变换后，可以得到电压方程为

uduquz1uz2=Rs0000Rs0000Rs0000Rsidiqiz1iz2+ddtψdψqψz1ψz2+－ωψqωψd00。（7）

电磁转矩方程为

Te=3pn［（Ld－Lq）idiq+ψfiq］。（8）

式中：pn为电机极对数；Te为电磁转矩；Ld为直轴电感；Lq为交轴电感；ψf为磁链。

以表贴式PMSM作为研究对象，电机电磁转矩Te和iq成正比，运动方程为

Te－TL－Bωm=Jdωmdt。（9）

式中：TL为负载施加的扭矩；B为阻尼系数；ωm为电动机的机械角速度；J为电动机的转动惯量。

由于能量变换只在α-β子空间进行，其余子空间将对电动机的谐波和损耗产生影响，因此需要采取适当的控制策略对α-β子空间变量进行控制，而对其余子空间变量进行抑制。

3 改进四矢量SVPWM

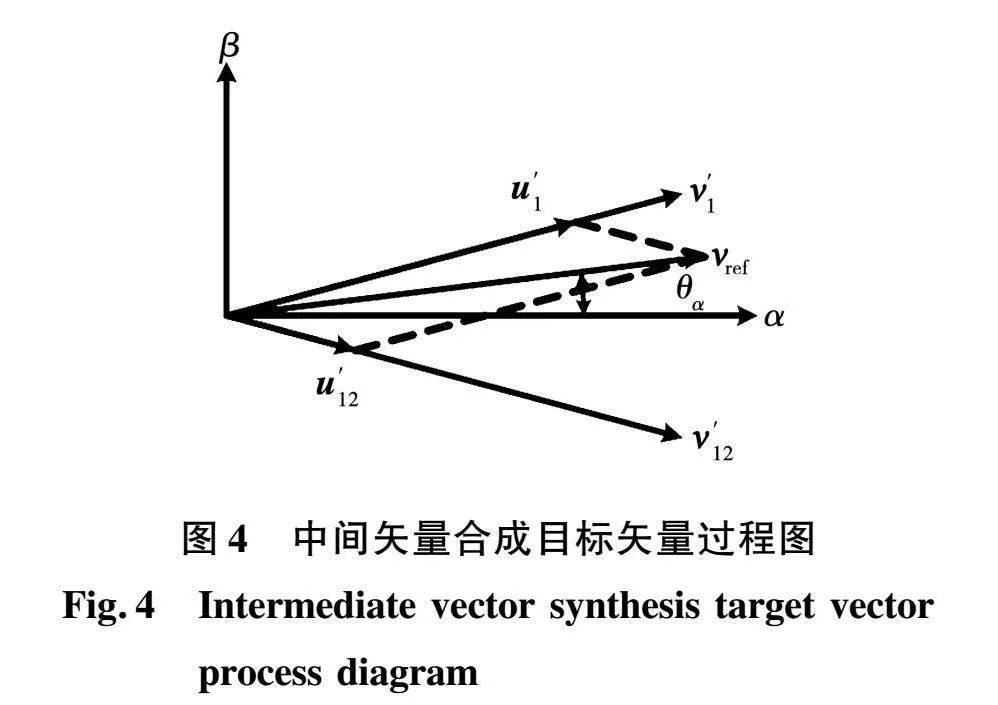
由文献[15]可知，假设目标矢量位于第一扇区，其相邻两个中间电压矢量为v′12和v′1，分布如图4所示。

图4中θα为目标矢量和α轴的夹角。在四矢量SVPWM算法中，设合成中间电压矢量v′1、v′12的基本电压矢量v1、v2、v3、v4的作用时间分别为T1、T2、T3、T4，表达式分别为：

T1=3（3－1）22VrefTsUdcsin（15°－θα）；

T2=3（3－1）22|vref|TsUdc［sin（θα+15°）+

3sin（15°－θα）］；

T3=3（3－1）22|vref|TsUdc［3sin（θα+15°）+sin（15°－θα）］；

T4=3（3－1）22|vref|TsUdcsin（θα+15°）。（10）

式中：Ts为开关周期；Udc为直流母线电压；θα为目标矢量与α轴的夹角。

3.1 直通平均分段改进四矢量SVPWM

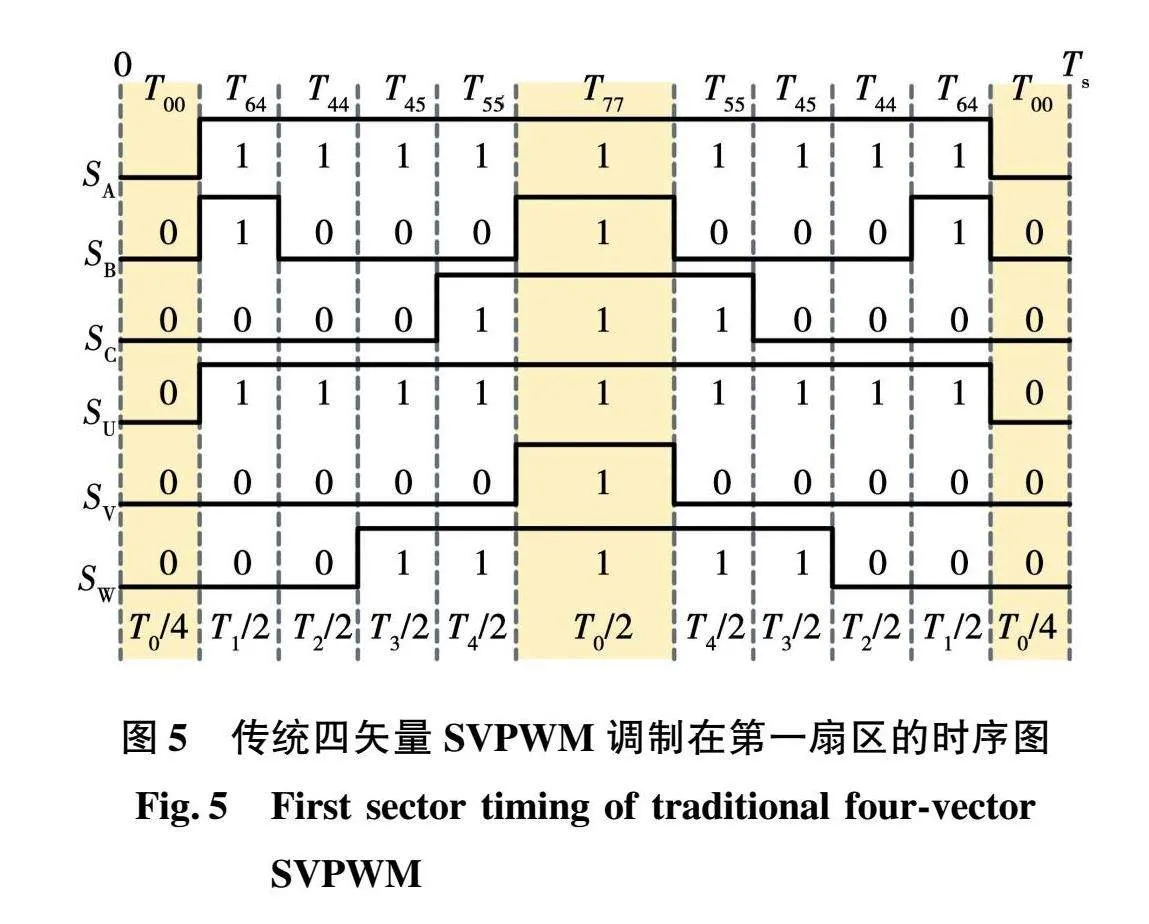
在传统四矢量SVPWM算法中插入直通时间可以实现QZSI的升压。传统四矢量SVPWM算法在第一扇区的时序如图5所示。

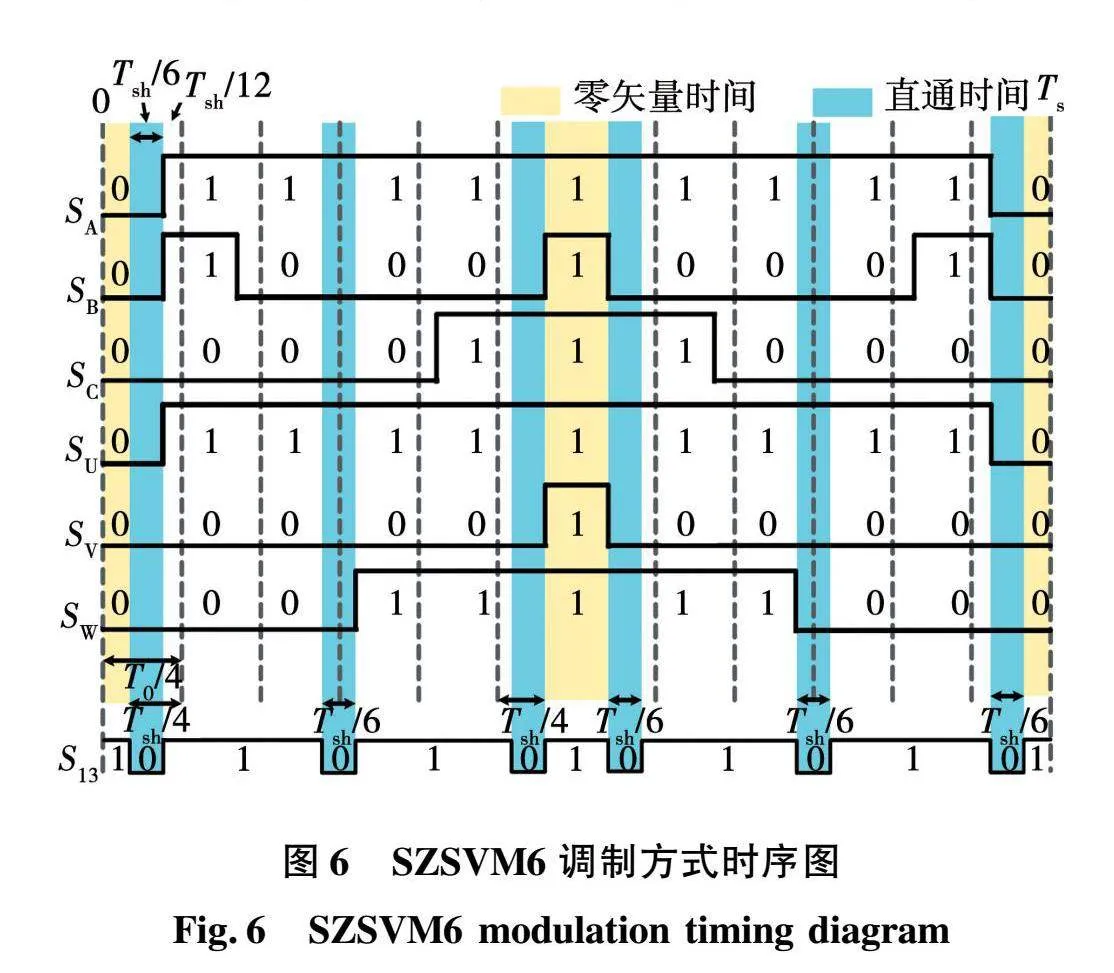
仿照三相准Z源逆变器的ZSVM6调制方式^[16]，对传统的四矢量SVPWM控制算法进行改进，将直通时间平均六分段插入到四矢量SVPWM中，记这种改进后的四矢量SVPWM调制方式为SZSVM6，以第一扇区为例的时序波形如图6所示。

这种方法是将直通时间平均分成六段，每一段的直通时间为Tsh/6。同时，由图6所示的SZSVM6调制方式时序图可以看出直通时间和零矢量时间之间的约束关系为

Tsh6+Tsh12≤T04，（11）

即

tsh≤T0。（12）

从式（12）可以看出， SZSVM6调制方式可以保证直通时间达到最大值，对零矢量的最大利用率可达100%，使准Z源逆变器升压能力达到最大。

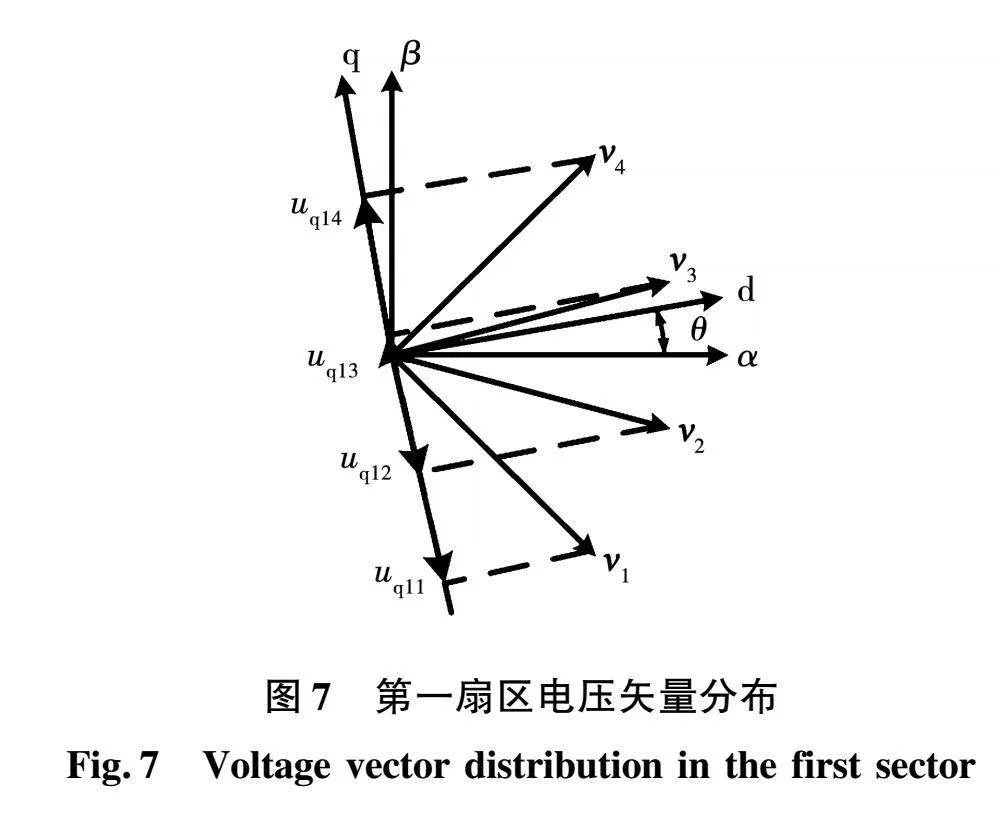
在第一个扇区内，4个基本矢量v1、v2、v3、v4的分布以及映射情况如图7所示。

将电压矢量v1、v2、v3、v4分别映射到q轴，由图7可以得到：

uq11=－Vsin（θ+45°）；

uq12=－Vsin（θ+15°）；

uq13=－Vsin（θ－15°）；

uq14=－Vsin（θ－45°）。（13）

式中：V=6（3－1）Udc/3；θ为d轴与α轴的夹角。

其他扇区的电压矢量映射到q轴上得到的分量为：

uqN1=－Vsin［θ+15°－（N－2）×30°］；

uqN2=－Vsin［θ+15°－（N－1）×30°］；

uqN3=－Vsin（θ+15°－N×30°）；

uqN4=－Vsin［θ+15°－（N+1）×30°］。（14）

式中N表示参考电压矢量所在扇区，N=1，2，…，12。

在i^*d=0控制方式下，由式（8）可以看出Te与iq成正比，因此，减小iq的脉动也就减小了Te的脉动。为了便于分析，认为电机处于正转稳态。

由式（7）可知，基于矢量空间解耦变换的六相PMSM在旋转坐标系下ud、uq的方程为

uduq=R00Ridiq+Ld00Lqddtidiq+－ωeLqiqωeLdid+ωeψf。（15）

对式（15）整理可以得到iq的变化率为

diqdt=1Lq（uq－Riq－ωeLdid－ωeψf）。（16）

在PMSM系统稳定运行时，可以认为在一个开关周期的初始时刻iq=i^*q、id=i^*d=0，对式（16）进行整理后可以得到在一个开关周期Ts内q轴电流值的表达式为

iq（t）－i*q=1Lq（uq－Ri*q－ωeψf）t。（17）

式中0≤t≤Ts。

当采用四矢量SVPWM算法时，在一个开关周期Ts内，目标矢量是由4个有效矢量（v1、v2、v3、v4）和一个零矢量v0合成的，其作用时间分别为T1、T2、T3、T4和T0。再结合式（14）可得出iq的增量与电压矢量的关系为

Δiqi=iq（Ti）－i*q=1Lq（uqNi－Ri*q－ωeψf）Ti。（18）

式中：i=0，1，2，3，4；uqNi为基本电压矢量vi的q轴分量；Ti为基本电压矢量vi的作用时间。

直通矢量和零矢量都不会产生有效电压分量，所以直通矢量产生的iq增量Δiqsh和零矢量产生的iq增量Δiq0的表达式分别为：

Δiqsh=－1Lq（Ri*q+ωeψf）Tsh；（19）

Δiq0=－1Lq（Ri*q+ωeψf）T0。（20）

式中Tsh为直通时间。

由式（19）、式（20）可知，当电机正转时，即ωegt;0，此时Δiqshlt;0，Δiq0lt;0。在一个开关周期内可以认为电机转速基本不变，则q轴电流维持在给定值附近波动，即

Δiq0+Δiq1+Δiq2+Δiq3+Δiq4=0。（21）

对上式进行整理可得

Δiq1+Δiq2+Δiq3+Δiq4=－Δiq0gt;0。（22）

式（22）表示一个开关周期内有效矢量对q轴电流产生的增量和为正值。

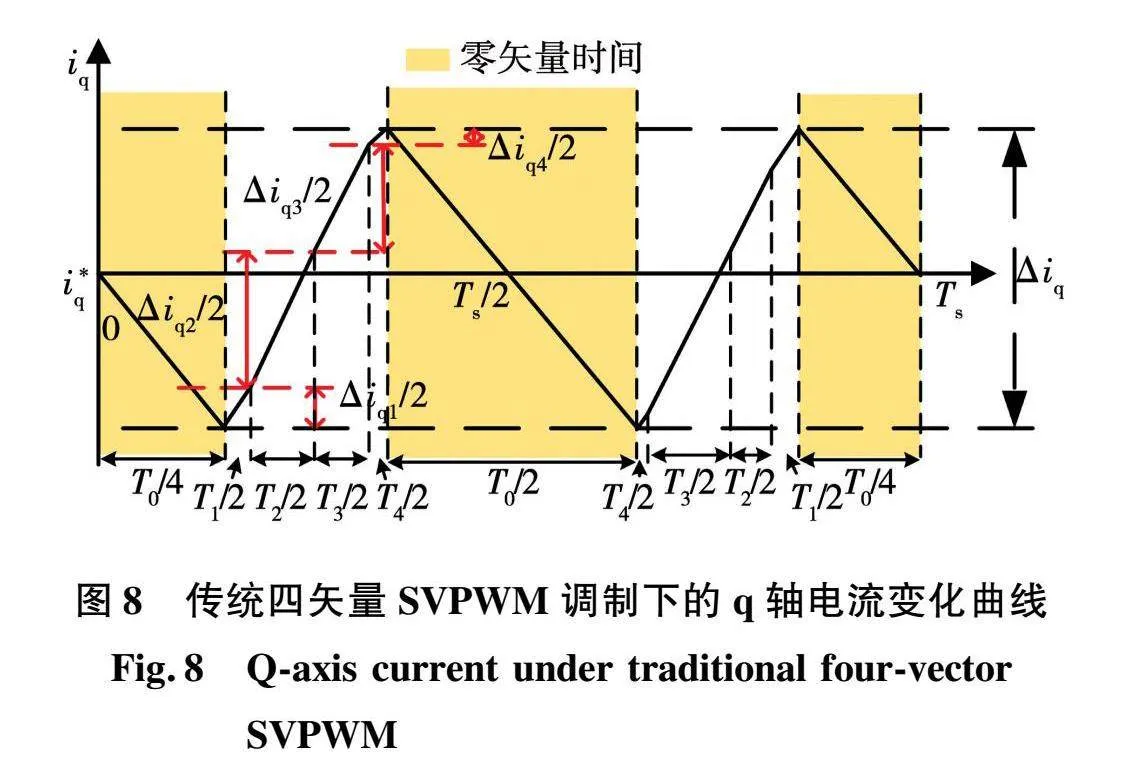
根据上述理论分析可以得出传统四矢量SVPWM调制方式下q轴电流在一个开关周期Ts内的变化轨迹，如图8所示。四矢量SVPWM控制算法在Ts内每段电压矢量作用时间相对于Ts/2呈对称分布，因此，在稳态时iq的变化在Ts内关于Ts/2中心对称。

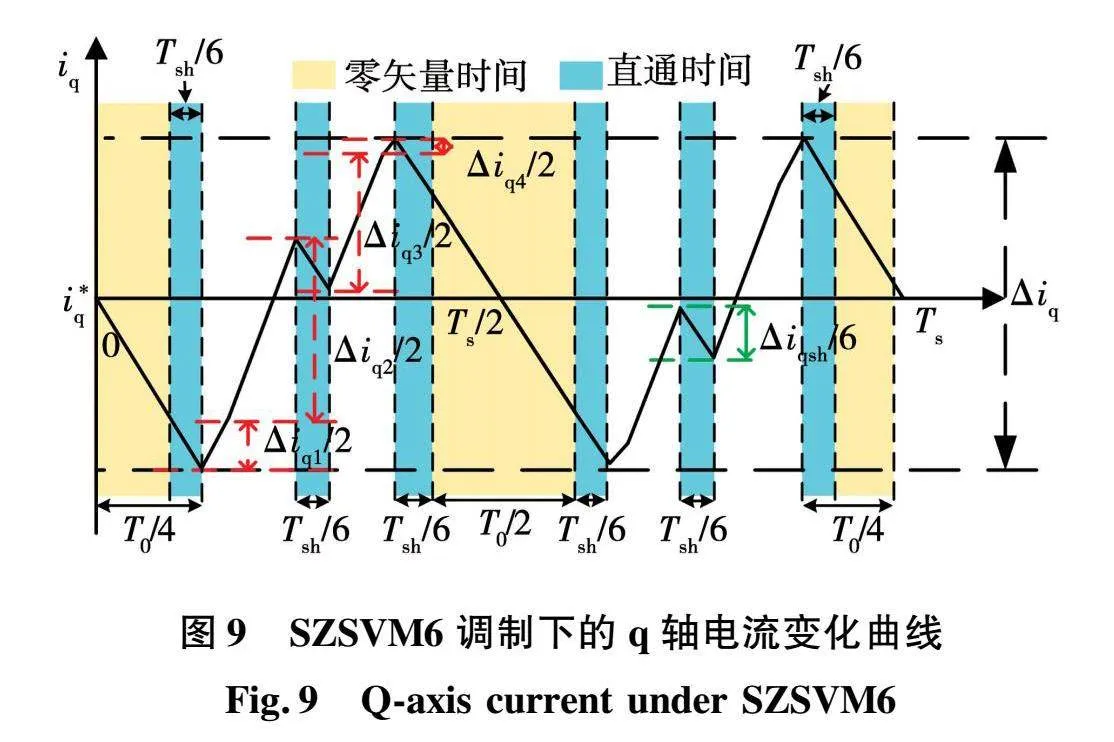
当采用SZSVM6调制时，根据图6所示的时序图可以得到SZSVM6调制下的q轴电流在一个开关周期内的轨迹，如图9所示。

与传统四矢量SVPWM相比，SZSVM6调制在有效矢量之间插入了Tsh/6的直通时间，使有效矢量对q轴电流的增量减小了Δiqsh/6，因此，SZSVM6的调制方式在每一个周期内都可以减小iq的脉动。

3.2 直通非平均分段改进四矢量SVPWM

通过前文分析可以得出，在有效矢量中插入直通矢量可以减小iq脉动，在SZSVM6调制下有效矢量之间的直通时间只有Tsh/6。为了进一步减小q轴电流的脉动，可以在有效矢量之间把所有的直通时间都插入进来。当总的直通时间相同时，在有效矢量中插入所有的直通时间，零矢量利用率可以达到100%，无论直通时间如何分段，每种分段方式下的零矢量与v1矢量切换时刻的q轴电流瞬时值都相同，v4矢量与零矢量切换时刻的q轴电流瞬时值也都相同。为了进一步利用直通矢量的灵活性来减小转矩脉动，同时考虑到有效矢量作用时对q轴电流产生的增量可以为负值，提出一种新的直通时间的计算方式，具体计算过程如下。

假设有效矢量v1、v2之间插入直通时间为Tsh1，其产生的q轴电流增量为Δiqsh1；在有效矢量v2、v3之间插入直通时间为Tsh2，其产生的q轴电流增量为Δiqsh2；在有效矢量v3、v4之间插入直通时间为Tsh3，其产生的q轴电流增量为Δiqsh3。

利用直通矢量对q轴电流产生的负增量来抵消有效矢量v1、v4作用时对q轴电流产生的增量，可以得到：

k1Δiq1=Δiqsh1；k2Δiq4=Δiqsh3。（23）

式中：k1=－1，Δiq1≥00，Δiq1≤0；k2=－1，Δiq4≥00，Δiq4≤0。

将式（18）和式（19）代入式（23）中可得：

k1Lq（uq1－Ri*q－ωeψf）T1=－1Lq（Ri*q+ωeψf）Tsh1；

k2Lq（uq4－Ri*q－ωeψf）T4=－1Lq（Ri*q+ωeψf）Tsh3。（24）

对式（24）整理后可得：

Tsh1=－k1uq1Ri*q+ωeψf－1T1；

Tsh3=－k2uq4Ri*q+ωeψf－1T4。（25）

如果Tsh1+Tsh3gt;Tsh，则需要通过式（25）进行如下处理：

Tsh1=Tsh1Tsh1+Tsh3Tsh；

Tsh3=Tsh3Tsh1+Tsh3Tsh。（26）

而Tsh2可以根据Tsh1和Tsh3计算得到，表达式为

Tsh2=Tsh－Tsh1－Tsh3。（27）

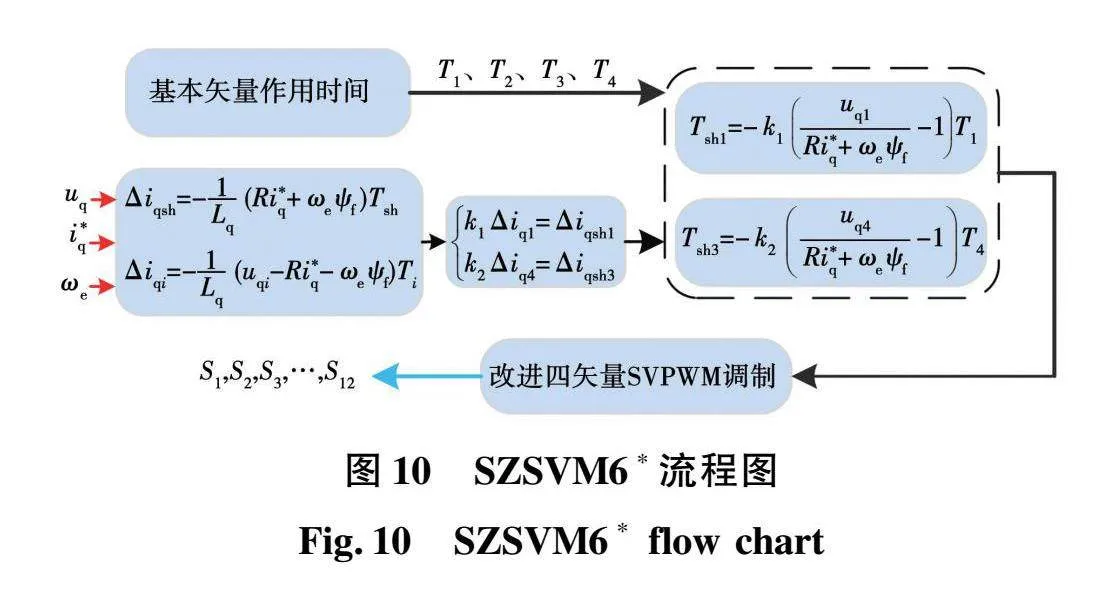
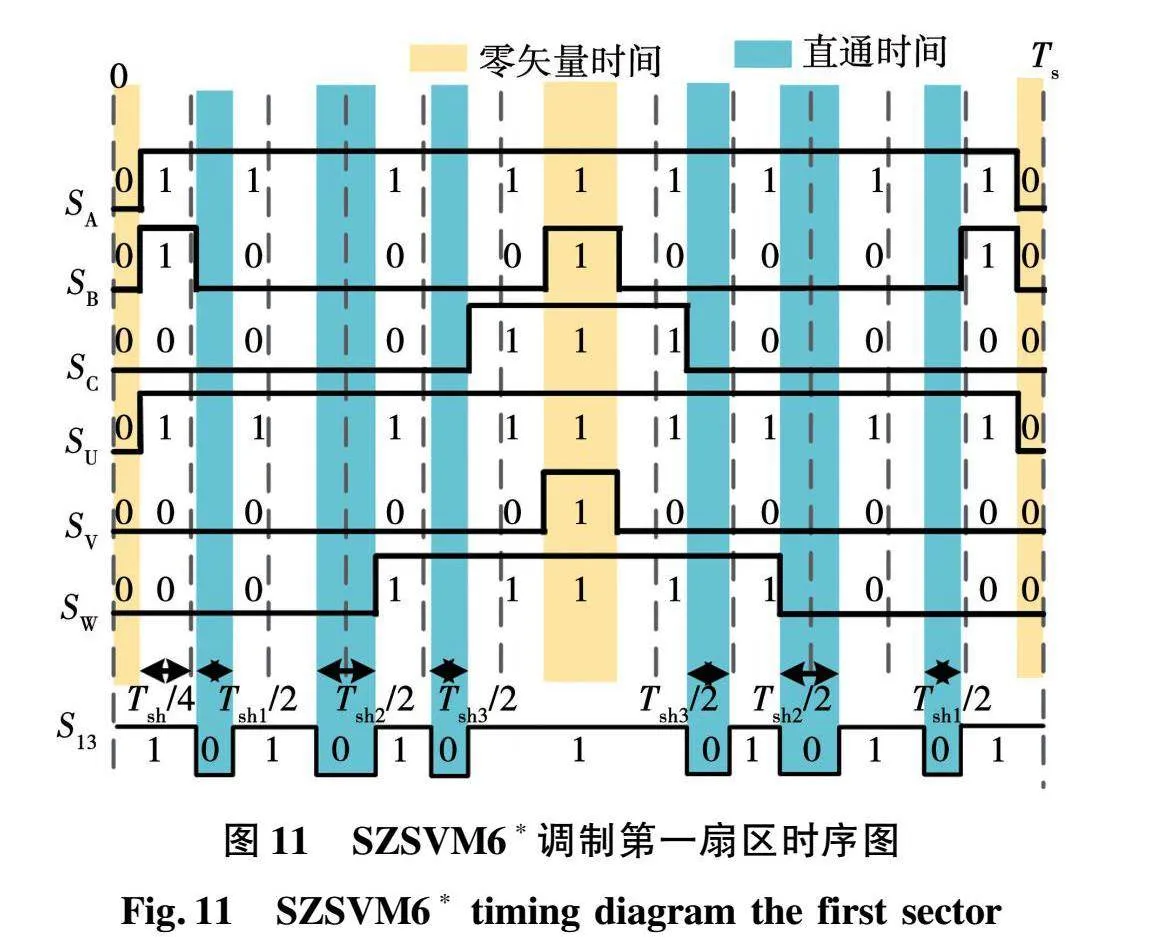
将上述计算得到的直通时间插入到四矢量SVPWM调制中，具体过程如图10所示，形成一种新的改进四矢量SVPWM调制，记为SZSVM6^*调制，如图11所示。

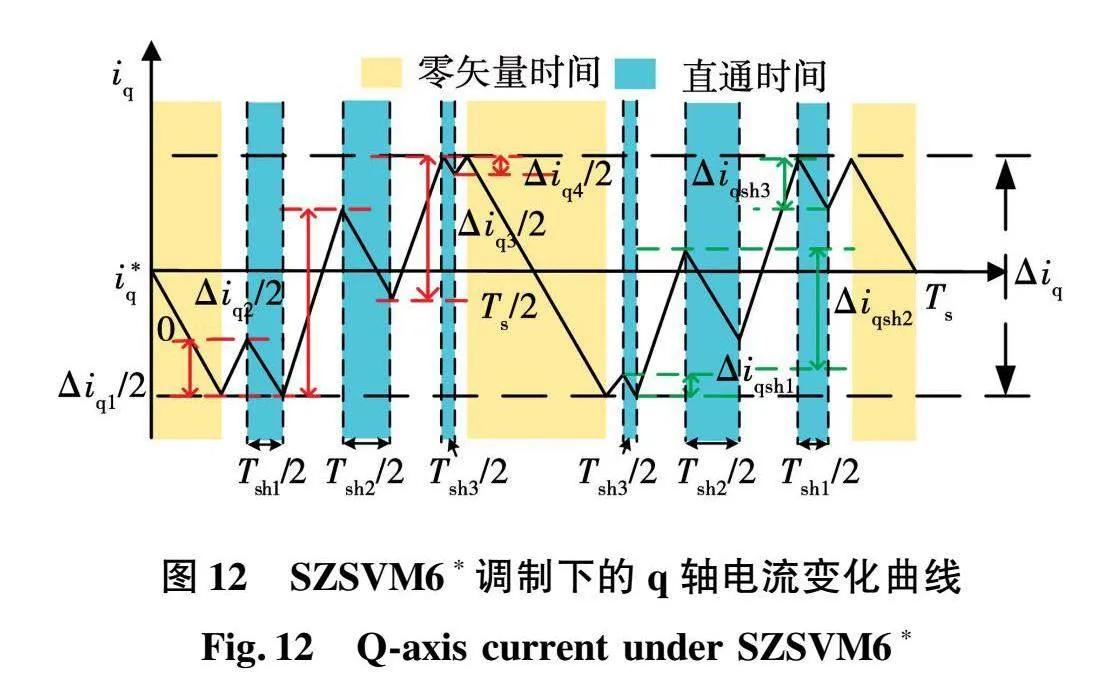
在SZSVM6^*调制方式下iq在一个开关周期内的变化曲线如图12所示。

与SZSVM6调制相比，SZSVM6^*调制将所有直通时间都插入到有效矢量之间，最大程度抵消有效矢量对q轴电流产生的增量，同时在一个开关周期内尽可能使q轴电流的实际值在参考值上下均匀分布，使q轴电流脉动更小，所以在SZSVM6^*调制方式下的电机转矩脉动更小。

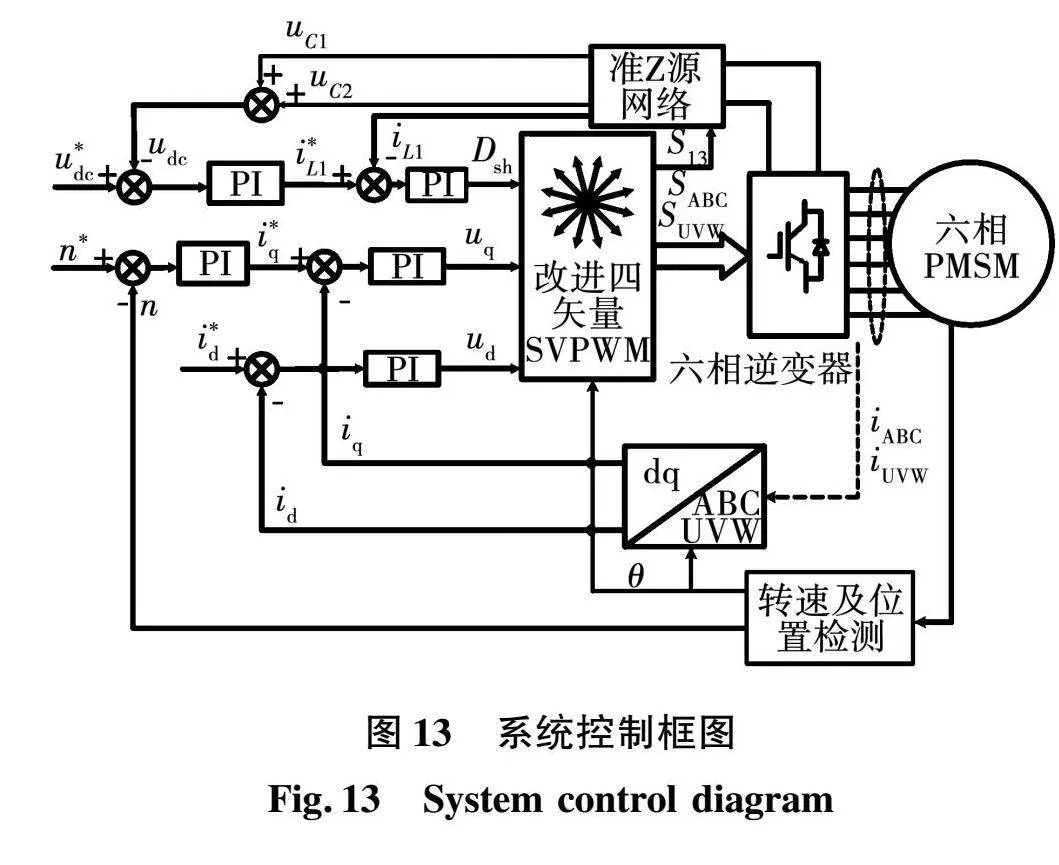
基于准Z源逆变器的六相PMSM系统的控制框图如图13所示，在对六相PWSM进行转速和电流双闭环控制的同时，也对准Z源网络进行电压和电感电流双闭环控制。

4 仿真分析

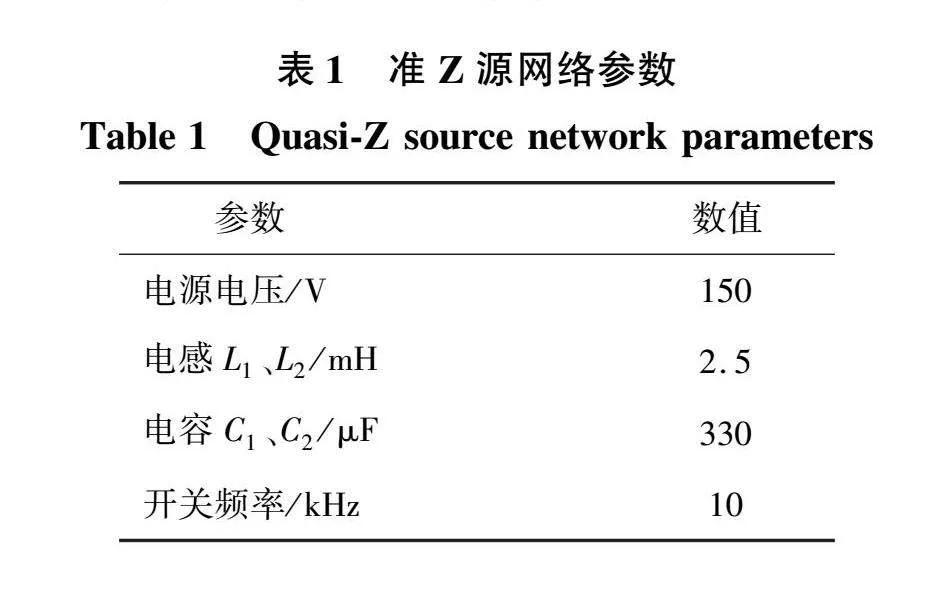
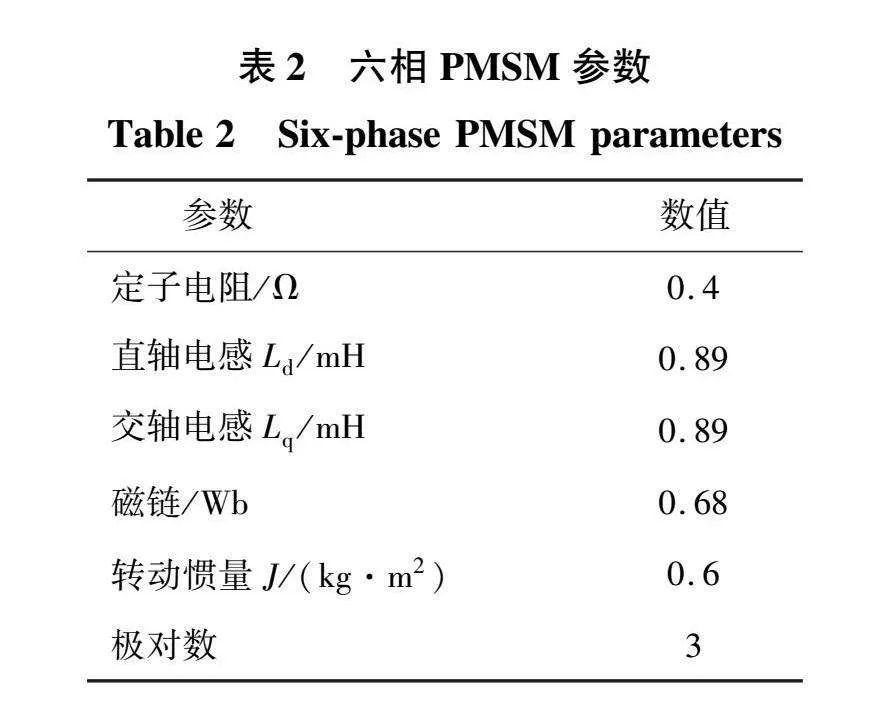
本节对上述理论进行仿真验证，在MATLAB/Simulink 中搭建系统的仿真模型，对传统SVPWM、SZSVM6和SZSVM6^*3种调制方式下系统的运行情况进行仿真对比。表1和表2分别为模型中准Z源网络的参数和电动机的参数。

4.1 改变电机转速仿真

下面对系统在传统SVPWM、SZSVM6和SZSVM6^*3种调制方式下改变电机转速时的运行情况进行仿真对比。将准Z源网络输出的直流链电压设定为250 V，电动机以100 r/min的转速启动，3 s时将转速增加到500 r/min，7 s后将转速降回100 r/min，可以得到仿真波形如图14～图16所示。

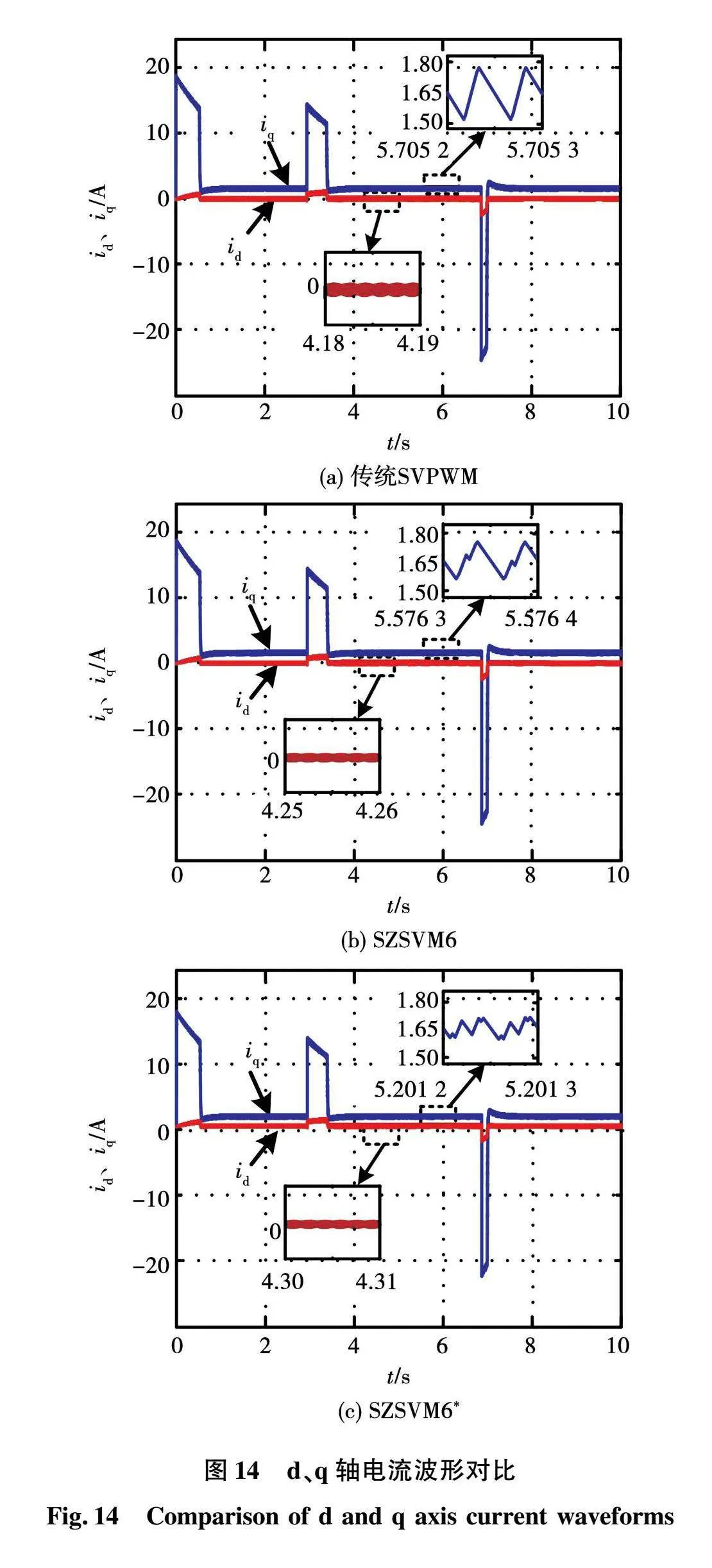
图14为3种调制算法时d、q轴电流波形。当转速发生突变时，3种调制算法下的系统d、q轴电流都发生了短暂的畸变，之后又恢复至稳态值。

从图14中可以看出，在传统SVPWM算法、SZSVM6算法以及SZSVM6^*算法下q轴电流脉动分别约为0.28、0.23和0.13 A。这表明SZSVM6^*算法对q轴电流脉动的抑制能力更强。3种调制策略下d轴电流波形基本相同。

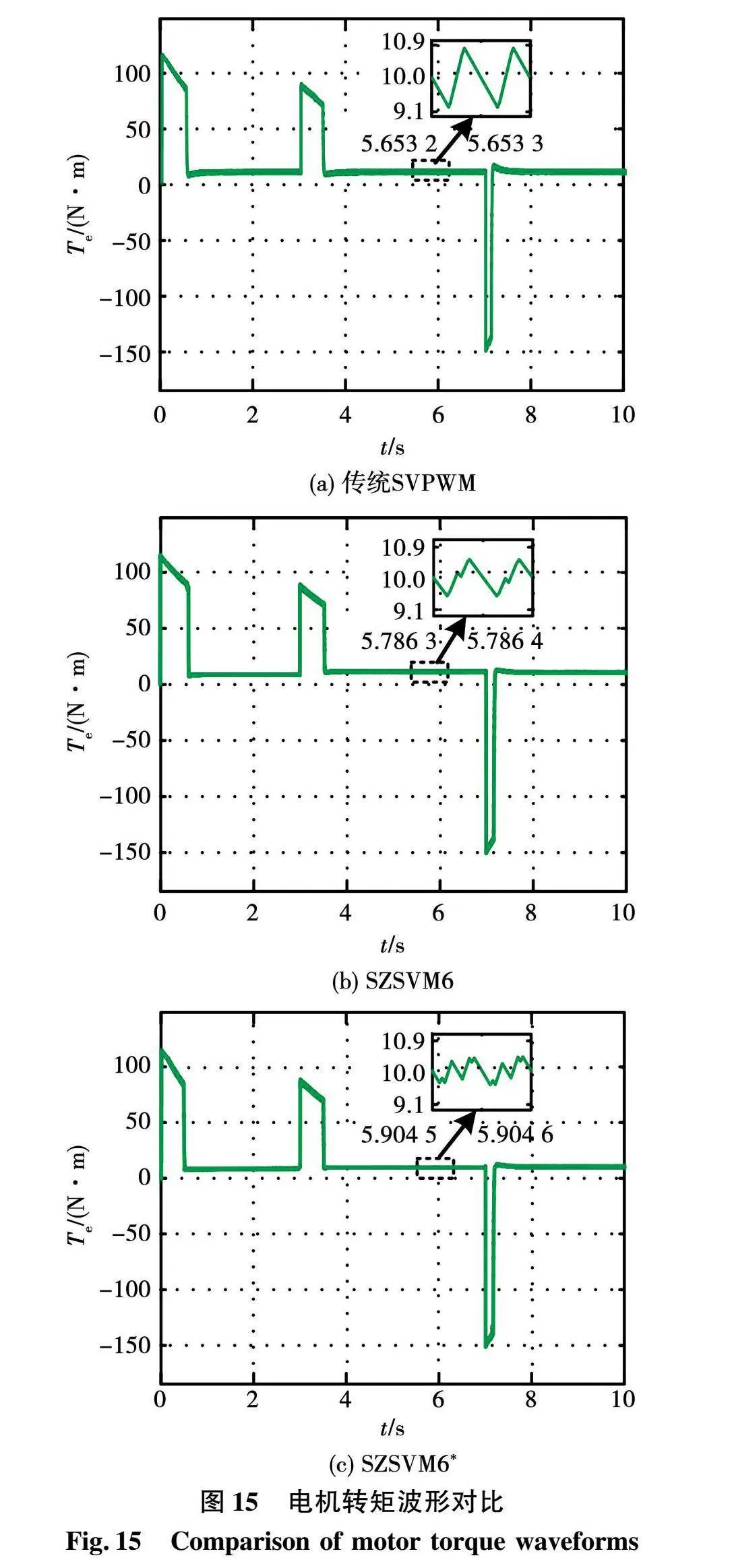
图15为3种调制算法下电机电磁转矩波形。当转速升高时，3种调制算法下电机的转矩都上升，但很短时间内转矩又恢复至稳定值。

从图15中可以看出，在传统SVPWM算法、SZSVM6算法以及SZSVM6^*算法下电机的转矩脉动分别约为1.8、1.3和1 N·m。这表明SZSVM6^*算法下电机的转矩脉动最小，而传统SVPWM算法下电机的转矩脉动最大。

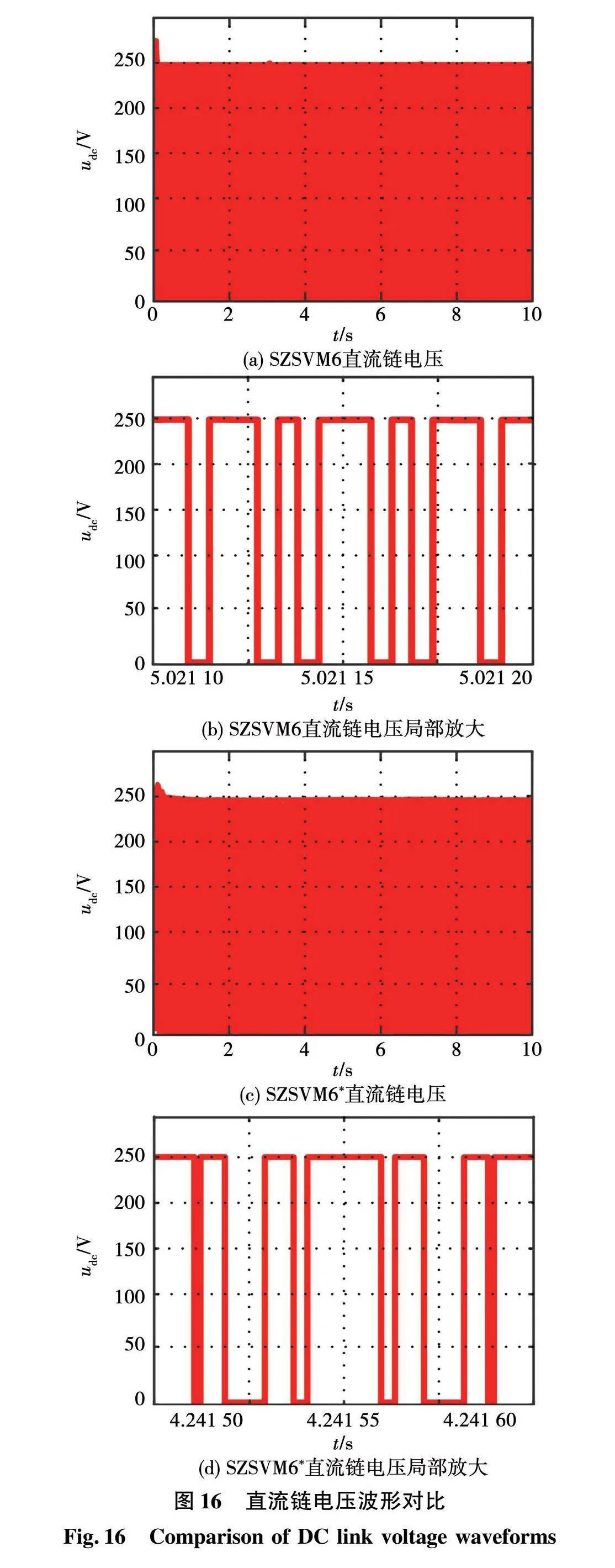
图16为基于准Z源逆变器的六相PMSM系统在SZSVM6和SZSVM6^*2种调制算法下的直流链电压波形。

从图16中可以看出，当电机转速发生改变时SZSVM6和SZSVM6^*2种算法下的直流链电压都没有较大波动，能够为电机提供稳定的电压。

4.2 负载突变仿真

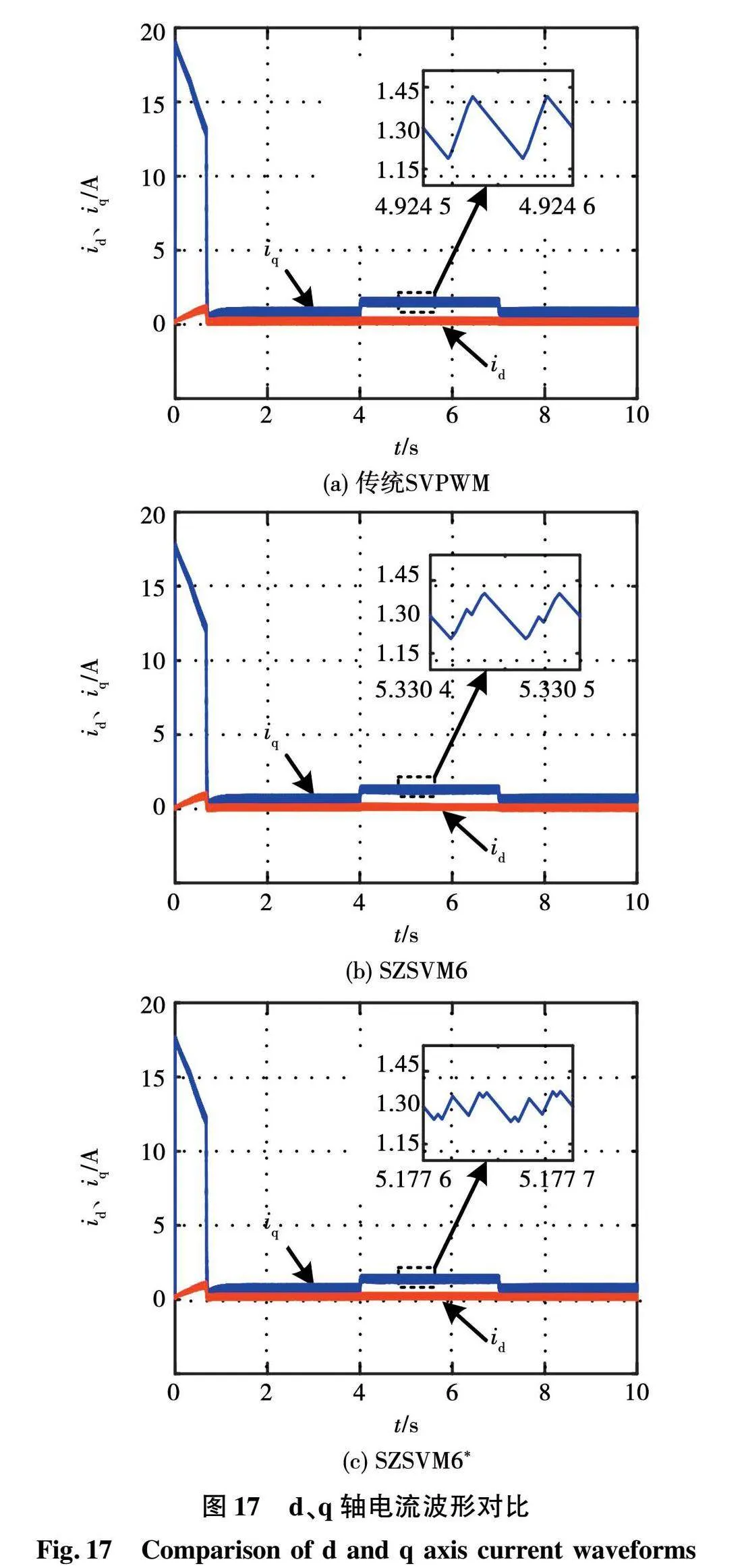
将电机的给定转速设置为500 r/min，电机带4 N·m负载启动，在4 s时负载从4 N·m增至8 N·m，7 s时负载下降至4 N·m，设置直流链电压给定值为250 V。可以得到仿真波形如图17和图18所示。

图17为负载突变时，3种调制算法下系统d、q轴电流波形。可以看出，当负载发生突变时3种调制算法下q轴电流都随负载增加（降低）而增加（降低），但在SZSVM6^*调制算法下系统的q轴电流脉动最小，传统SVPWM算法下系统的q轴脉动最大。

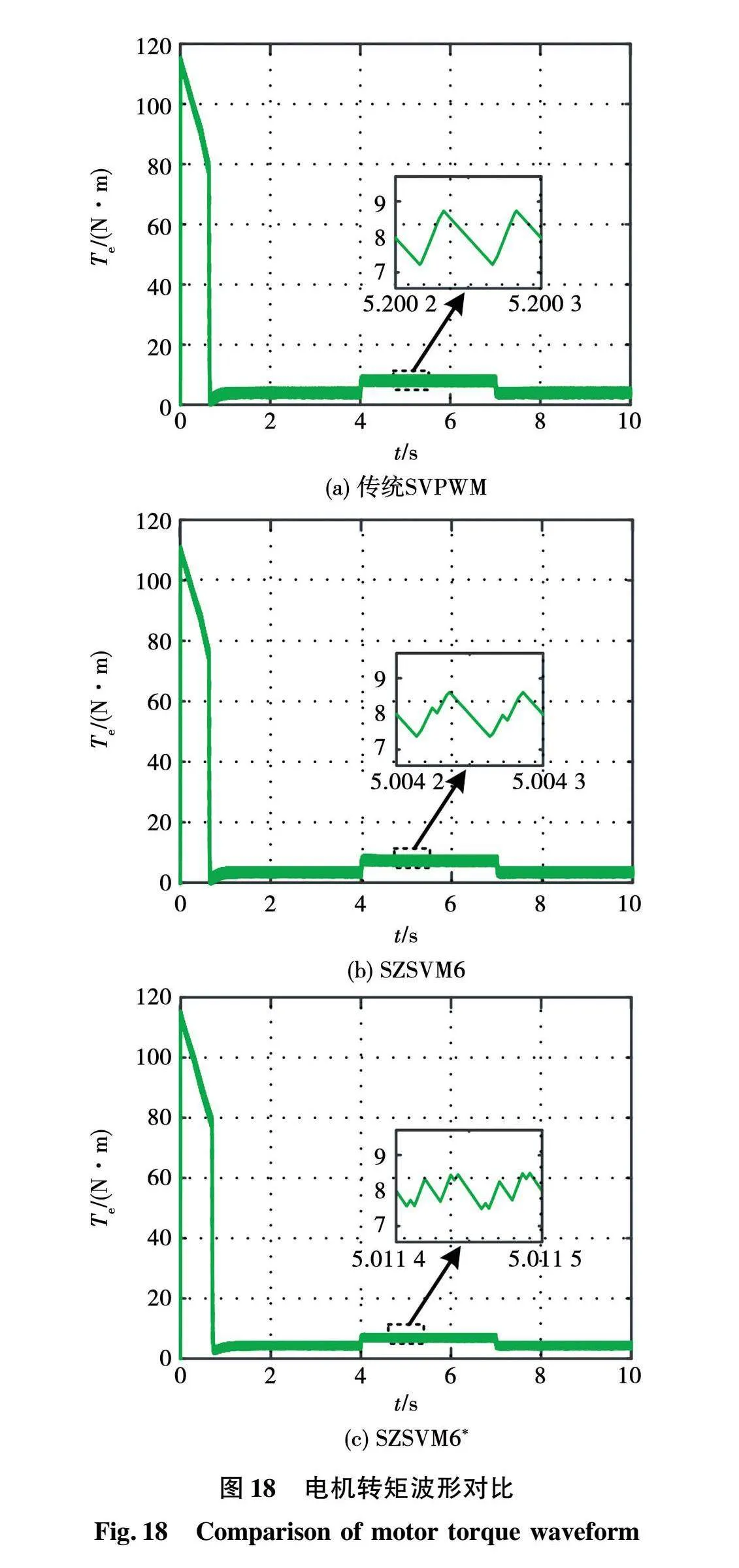
3种调制算法下电机电磁转矩的波形对比如图18所示。由图18可知，当改变负载时，3种调制算法下系统转矩脉动较为平稳，无较大突变。可以看出，在传统SVPWM、SZSVM6和SZSVM6^*调制方式下电机的转矩脉动分别约为1.7、1.2和1.1 N·m，结果表明SZSVM6^*算法下系统转矩脉动最小。

从图14～图18的仿真结果可以看出，基于准Z源逆变器的六相永磁同步电机系统在改变转速和负载突变时都能保持系统稳定运行，并且提出的控制策略可以抑制电机的转矩脉动。

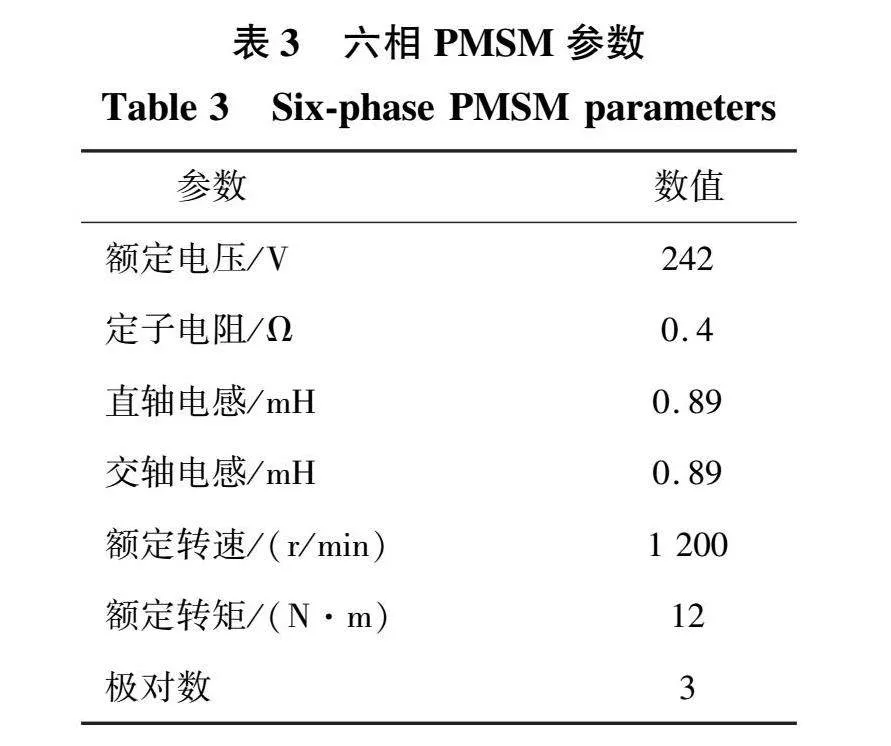
5 实验验证

实验中使用的电机参数如表3所示。阻抗源网络中两个电感的取值均为2.5 mH，两个电容的取值为330 μF，将逆变器的直通占空比设置为0.2，系统输入的直流稳压电源电压为150 V，则准Z源网络输出直流链电压为250 V。

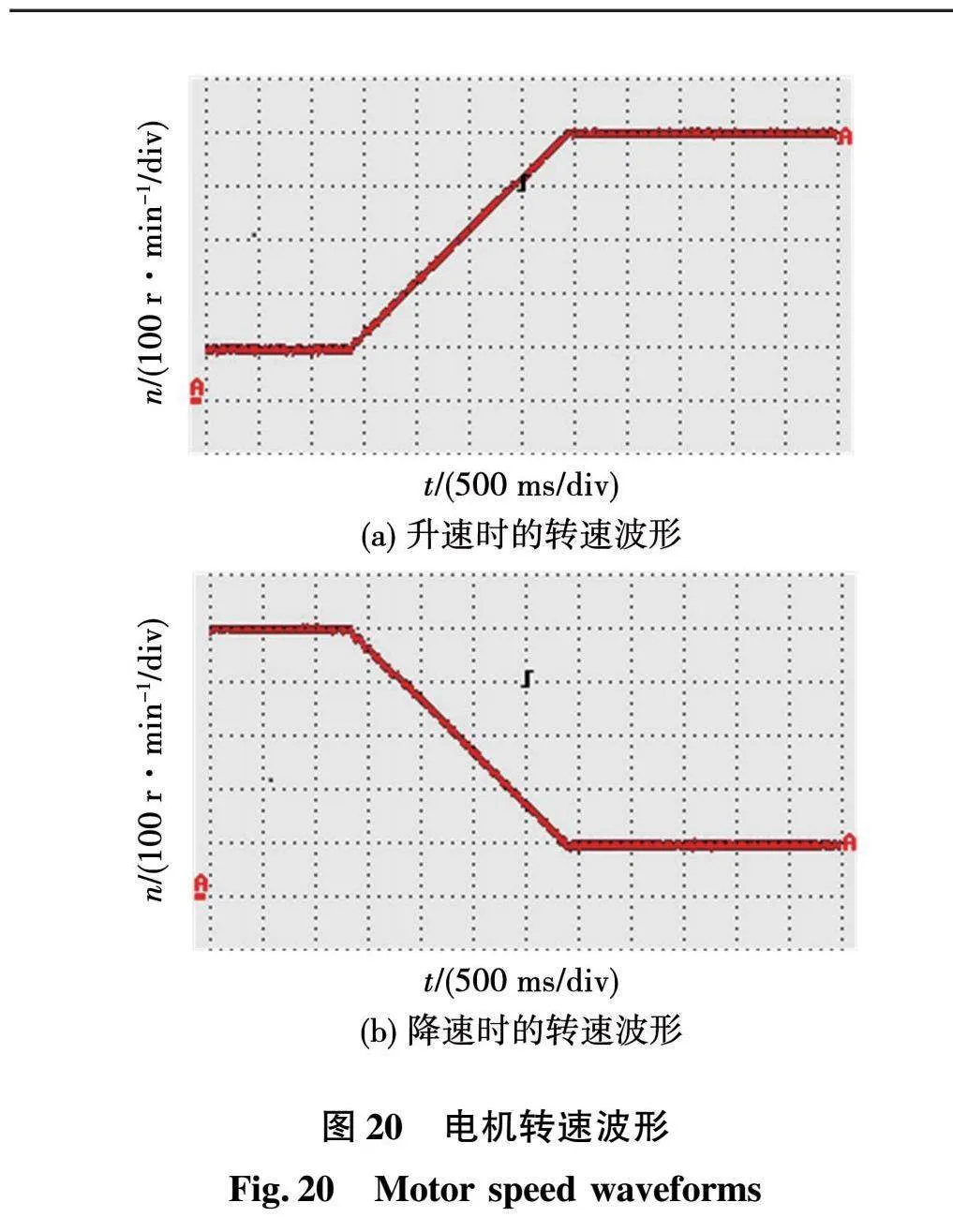
本实验搭建的基于准Z源逆变器的六相PMSM系统的实验平台如图19所示。首先对基于准Z源逆变器的六相PMSM系统进行升降速实验。负载为10 N·m，在SZSVM6调制方式下，并对PWM波进行中心化处理，设置电机给定转速为500 r/min，当电动机实际转速上升到500 r/min并且达到稳定运行后，再将电动机的给定转速降回100 r/min，得到的转速波形如图20所示。

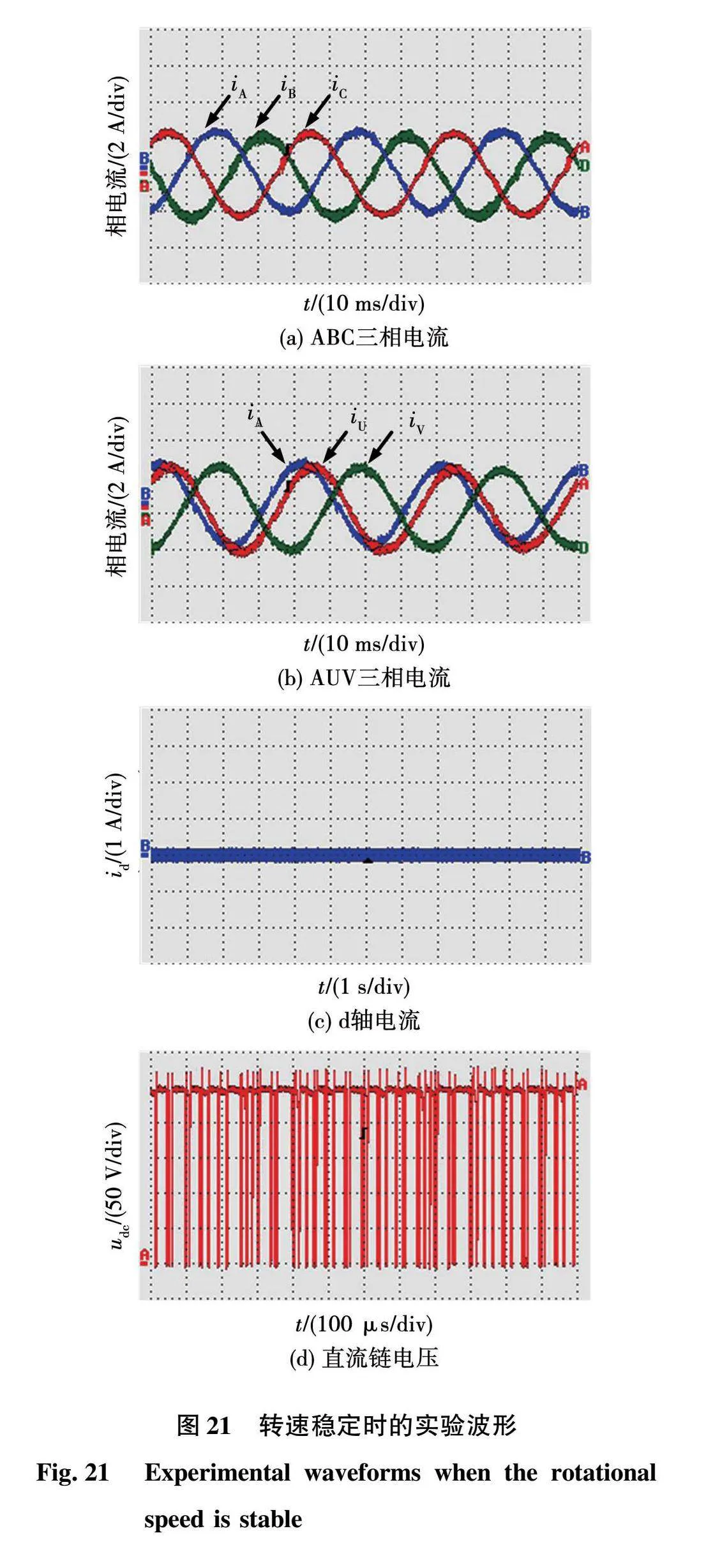
考虑安全因素在程序中设置了转速斜坡给定，所以在图20中无论转速上升还是下降都是按照斜坡变化。从图20中可以看出，电机的加速和减速过程都比较平稳，转速几乎没有超调，在转速达到给定值后波动很小。当转速稳定在500 r/min时，得到如图21所示的实验波形。

图21（a）和图21（b）为六相PMSM相电流波形，六相电流幅值均相等，A、B、C三相电流的相位依次相差120°，A相与U相电流相位相差的角度为30°，电机稳定运行时相电流波形有少许尖刺，整体较为平滑。图21（c）为d轴电流波形，本实验采用的是i^*d=0控制，d轴电流在零附近有较小波动，d轴电流闭环效果良好。图21（d）为直流链电压波形，阻抗源网络输出的直流链电压幅值约为250 V，波形有些许高频尖刺。

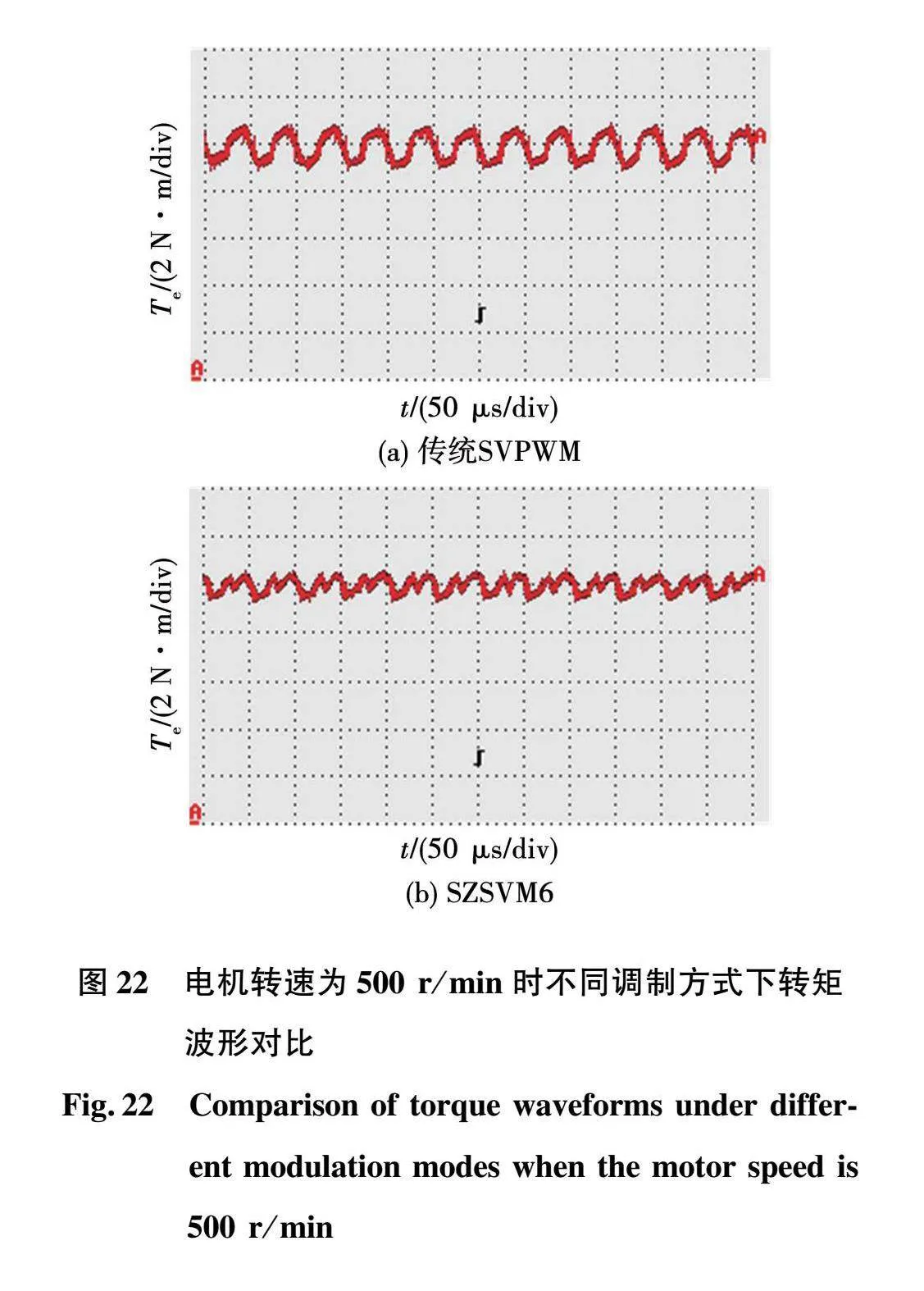
对系统在传统SVPWM和SZSVM6两种调制方式下的电机转矩进行对比，在电机转速稳定在500 r/min时，得到的波形如图22所示，在传统SVPWM和SZSVM6调制方式下电机的转矩脉动分别约为1.7和1.1 N·m，在SZSVM6调制方式下，系统的整体运行效率为95.07%。

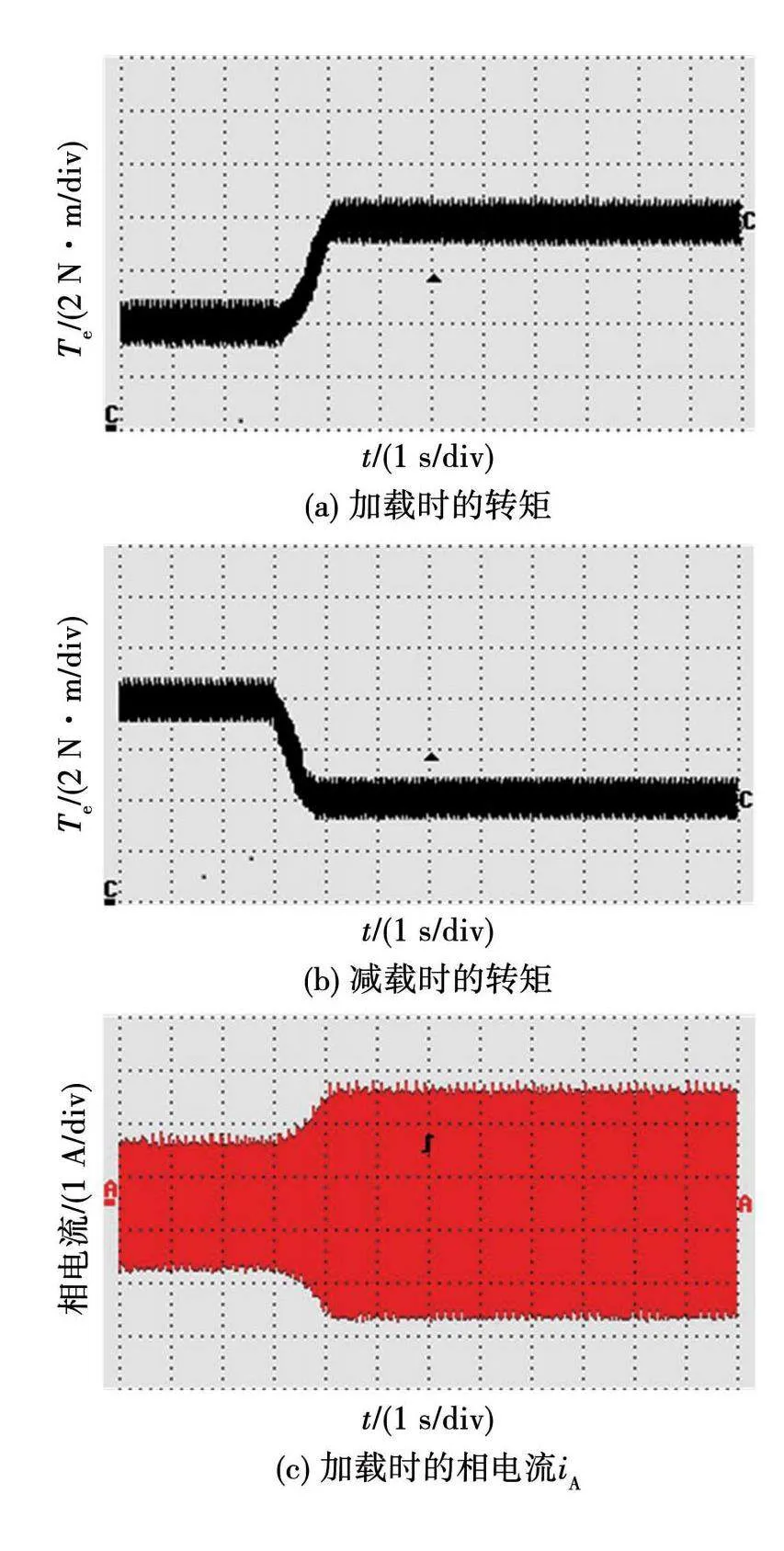
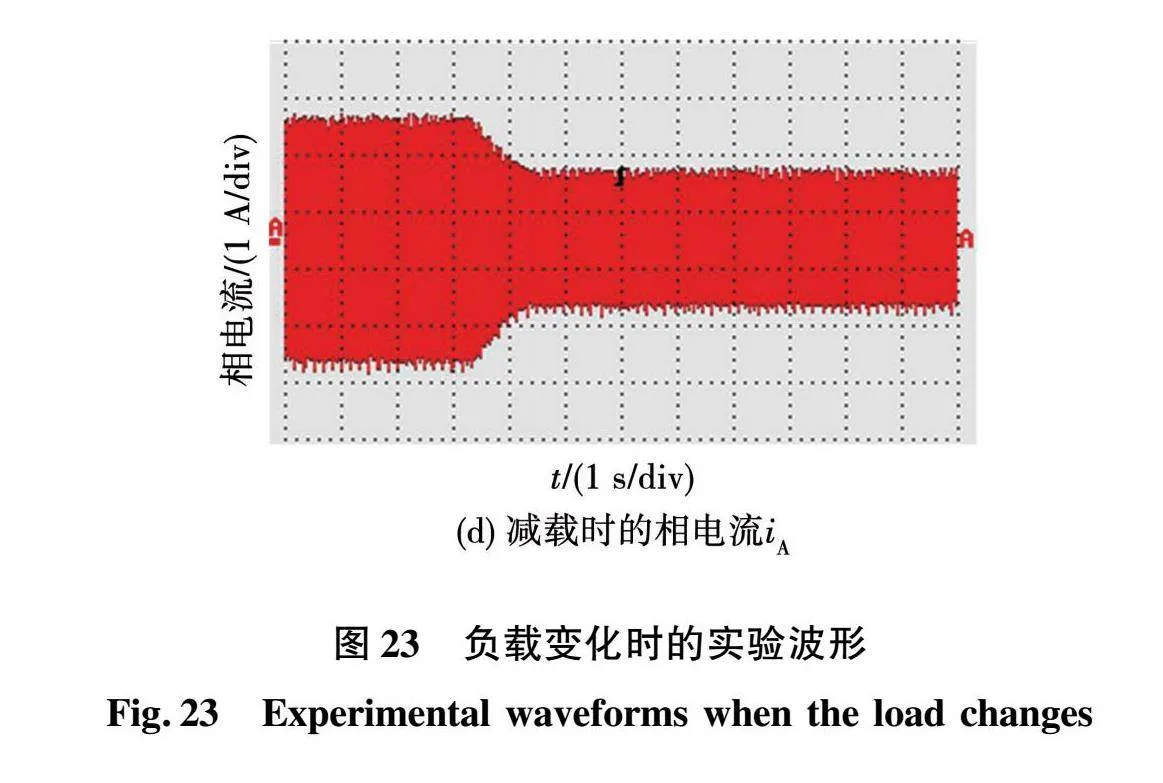
然后在SZSVM6调制方式下进行加减载实验。当电机转速稳定在500 r/min时，调节磁粉制动器旋钮将负载从4 N·m缓慢增至8 N·m，待系统稳定后再将负载降至4 N·m，得到的实验波形如图23所示。

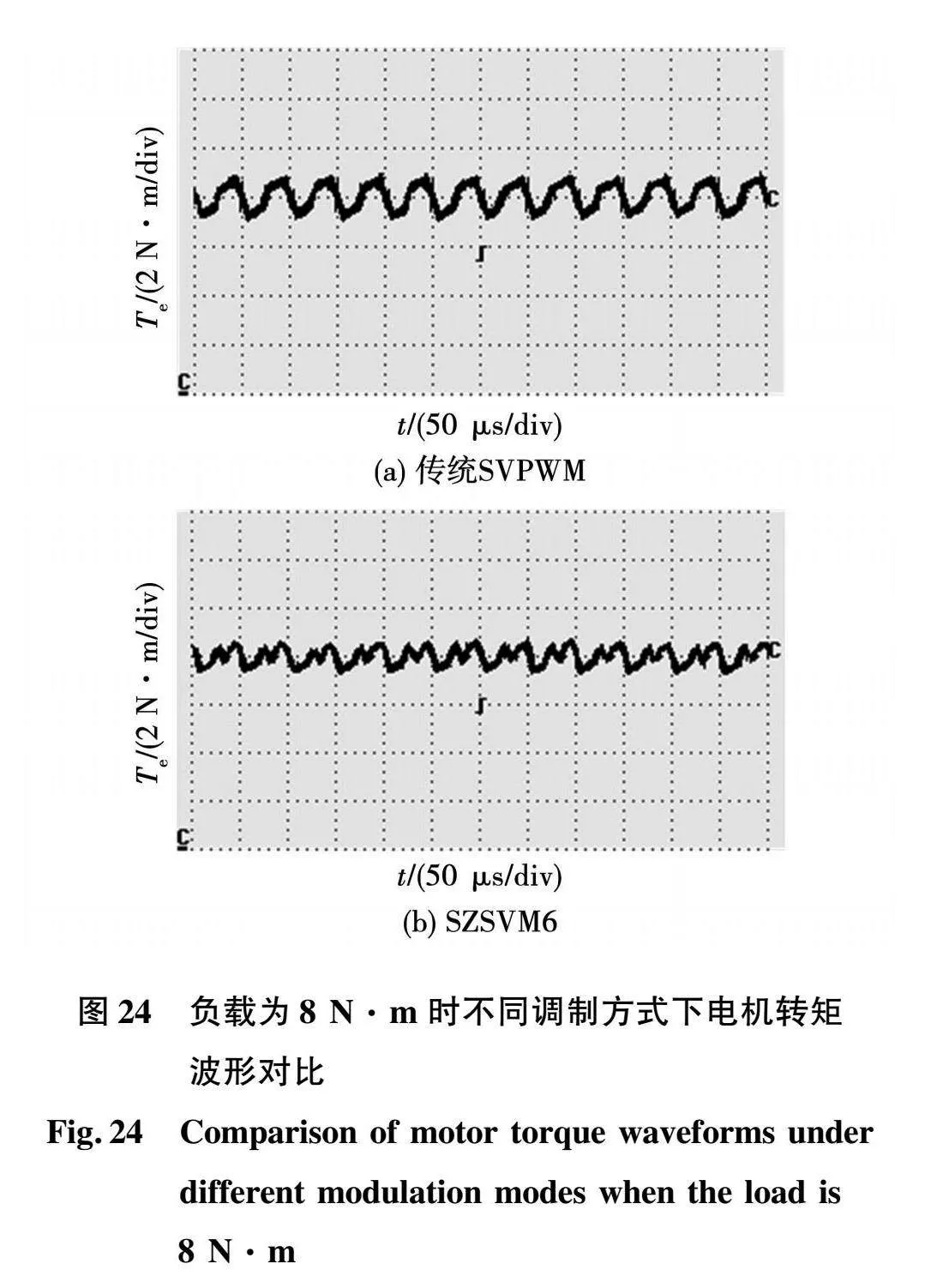
图23（a）和图23（b）为转矩波形，电机转矩随负载变化而变化，基本没有超调，表明系统可以输出稳定的电磁转矩。图23（c）和图23（d）为负载变化时电机相电流波形，相电流幅值跟负载大小成正比关系。下面对系统在两种调制方式下的电机转矩波形进行对比，当负载调节到8 N·m时，得到的波形如图24所示，在传统SVPWM和SZSVM6调制方式下电机的转矩脉动分别约为1.6和1.2 N·m。

从图22和图24可以看出，相较于传统SVPWM调制方式，SZSVM6调制方式能够减小转矩脉动，使电机的转矩更加稳定。由此可见提出的调制策略能够有效地降低电机的转矩脉动。

6 结 论

本文以基于准Z源逆变器的六相PMSM系统作为对象，针对低转矩脉动的改进四矢量SVPWM调制策略展开研究。

首先，分析准Z源逆变器的工作原理、非对称六相PMSM的数学模型以及四矢量SVPWM的工作原理；其次，提出直通平均分段的四矢量SVPWM调制方式，推导各电压矢量作用时对q轴电流的影响；再次，从减小转矩脉动角度出发，提出一种直通非平均分段的改进四矢量SVPWM调制策略，将计算得到的直通时间插入到四矢量SVPWM调制中，电动机的转矩脉动得到了有效抑制；最后，通过仿真及实验进行验证，结果表明，加入准Z源网络的六相电机控制系统具备升压能力，所提出的改进四矢量SVPWM调制策略能够有效降低电机的转矩脉动，且效率可达95%，提高了电机系统的动静态性能。

参 考 文 献：

［1］ 谭凯文. 基于准Z源逆变器的永磁同步电机驱动控制系统研究[D]. 哈尔滨：哈尔滨工业大学， 2021.

［2］ SHIM J， CHOI H， HA J I. Zero-sequence current suppression with dead-time compensation control in open-end winding PMSM[C]//2020 IEEE Energy Conversion Congress and Exposition （ECCE）， October 11-15， 2020， Detroit， MI， USA. 2020： 3051-3056.

［3］ 彭方正， 房绪鹏， 顾斌，等. Z源变换器[J]. 电工技术学报， 2004， 19（2）： 47.

PENG Fangzheng， FANG Xupeng， GU Bin， et al. Z-source inverter[J].Transactions of China Electrotechnical Society， 2004， 19（2）： 47.

［4］ 蔡春伟， 曲延滨， 盛况. 准Z源逆变器的暂态建模与分析[J]. 电机与控制学报， 2011， 15（10）： 7.

CAI Chunwei， QU Yanbin， SHENG Kuang. Transient modeling and analysis of quasi-Z-source inverter[J]. Electric Machines and Control， 2011， 15（10）： 7.

［5］ 王固萍， 叶培乐， 王斌， 等. 高增益准Z源网络间接矩阵变换器的结构研究[J]. 电机与控制学报， 2021， 25（12）： 127.

WANG Guping， YE Peile， WANG Bin， et al. Research on structure of high gain indirect matrix converter with quasi-Z source networks[J].Electric Machines and Control， 2021， 25（12）： 127.

［6］ 赵安邦， 房成群， 袁成功. 一种改进Cockcroft-Walton准Z源逆变器[J]. 电工技术， 2019， 23（8）： 36.

ZHAO Anbang， FANG Chengqun， YUAN Chenggong. An improved Cockcroft-Walton quasi Z-source Inverter[J]. Electric Engineering， 2019，23（8）： 36.

［7］ 刘贇， 丁新平， 赵德林， 等. 新型倍压-Z源逆变器[J]. 太阳能学报， 2021， 42（8）： 133.

LIU Yun， DING Xinping， ZHAO Delin， et al. New type double voltage Z-source inverter[J]. Acta Energiae Solaris Sinica， 2021， 42（8）： 133.

［8］ 吴昊坤， 黄科元， 吕维， 等. 用于高速永磁电机的Z源逆变器直流链电压控制策略[J]. 电工技术学报， 2020， 35（16）： 3489.

WU Haokun， HUANG Keyuan， L Wei， et al. DC-link voltage control strategy of Z-source inverter for high-speed permanent magnet motor[J].Transactions of China Electrotechnical Society， 2020， 35（16）： 3489.

［9］ 颜景斌， 朴晶琳， 李冠达， 等. 改进ADRC的增强型双向Z源逆变器直流链电压控制[J]. 哈尔滨理工大学学报， 2020， 25（6）： 77.

YAN Jingbin， PIAO Jinglin， LI Guanda， et al. DC link voltage control of enhanced bidirectional Z source inverter with improved ADRC[J]. Journal of Harbin University of Science and Technology， 2020， 25（6）： 77.

［10］ GHAHDERIJANI M M， DEHKORDI B M. Comprehensive robust and fast control of Z-source-inverter-based interior permanent magnet synchronous motor drive system[J]. IEEE Transactions on Industrial Electronics， 2020， 68（12）： 11783.

［11］ 陈艳， 曹展豪， 胡磊， 等. 准Z源逆变器中抑制二次谐波电流的虚拟阻抗控制策略[J]. 电机与控制学报， 2023， 27（6）： 137.

CHEN Yan， CAO Zhanhao， HU Lei， et al. Virtual impedance control strategy for suppressing second harmonic current in quasi-Z-source inverter[J]. Electric Machines and Control， 2023， 27（6）： 137.

［12］ HAMMAD R， DABOUR S， RASHAD E. Z-source inverters for asymmetrical six-phase drives with reduced switching losses[C]//2019 IEEE Conference on Power Electronics and Renewable Energy （CPERE）， October 23-25， 2019，Aswan， Egypt. 2019： 491-496.

［13］ HAMMAD R， DABOUR S， RASHAD E. Asymmetrical six-phase induction motor drives based on Z-source inverters： modulation， design， fault detection and tolerance[J]. Alexandria Engineering Journal， 2022， 61（12）： 10055.

［14］ FATEMI S M J R， SOLTANI J， ABJADI N R， et al. Space-vector pulse-width modulation of a Z-source six-phase inverter with neural network classification[J]. IET Power Electronics， 2012， 5（9）： 1956.

［15］ 庞仁江. 基于六相永磁同步电机SVPWM算法的ASIC设计[D]. 成都：电子科技大学， 2020.

［16］ XIAO S， GU X， WANG Z， et al. A novel variable DC-link voltage control method for PMSM driven by a quasi-Z-source inverter[J].IEEE Transactions on Power Electronics，2019，35（4）：3878.

（编辑：邱赫男）