基于Mel-CNN和电流频谱的电机轴承外圈故障声纹检测方法

摘 要：外轴承滚道缺陷是电机轴承的一种高发故障。针对如何高效检测外轴承滚道故障，提出一种基于Mel-CNN和电流频谱的轴承外圈故障声纹检测方法，首先构造外轴承滚道缺陷导致的径向转子运动机制，采集正常与故障状态下的定子电流，并使用小波阈值去噪排除噪声成分。其次，利用鲸鱼算法（WOA）优化变分模态分解（VMD）去除电机噪声中的高频成分，提取Mel谱声纹特征。最后，利用卷积神经网络（CNN）重新提取Mel声纹特征，获取表征轴承外圈故障的高维抽象特征并利用声纹融合电流神经网络模型对轴承进行故障诊断。结果表明，Mel谱结合电流频谱特征能够准确地表征轴承外圈故障。该方法通过对数据集的学习，有效区分了故障状态和健康状态，完善了神经网络在检测异步电动机轴承外圈故障中的缺陷。

关键词：Mel声纹特征；电流频谱；卷积神经网络；轴承外圈故障；变分模态分解；鲸鱼算法

DOI：10.15938/j.emc.2024.11.007

中图分类号：TM346

文献标志码：A

文章编号：1007-449X（2024）11-0068-13

Voiceprint detection method for motor bearing outer ring fault based on Mel-CNN and current spectrum

BAO Xiaohua¹， WANG Shuo¹， GUAN Bokai¹， WANG Zihao¹， QIU Haotian¹， YANG Dongliang²

（1.School of Electrical and Automation Engineering， Hefei University of Technology， Hefei 230009， China；2.Hefei Hengda Jianghai Pump Co.， Ltd.， Hefei 231131， China）

Abstract：The defect of the outer bearing raceway is a common fault of motor bearings. A bearing outer ring fault voiceprint detection method based on mel-convolutional neural network （Mel-CNN） and current spectrum was proposed to efficiently detect outer bearing raceway faults. Firstly， the radial rotor motion mechanism caused by outer bearing raceway defects was constructed， and the stator currents under normal and fault conditions are collected. Wavelet threshold denoising was used to eliminate noise components. Secondly， the whale optimization algorithm （WOA） was used to optimize variational mode decomposition （VMD） to remove high-frequency components from motor noise and extract Mel spectral voiceprint features. Finally， the convolutional neural network （CNN） was used to extract Mel voiceprint features once again， obtain high-dimensional abstract features that represent the fault of the bearing outer ring， and use the voiceprint fusion current neural network model for bearing fault diagnosis. The results indicate that Mel spectrum combined with current spectrum characteristics can accurately characterize the fault of the bearing outer ring. The method effectively distinguishes between faulty and healthy states by learning from the data set， and perfects the defects of neural networks in detecting faults in the outer ring of asynchronous motor bearings.

Keywords：Mel voiceprint features; current spectrum; convolutional neural network; outer ring bearing failure; variational modal decomposition; whale optimization algorithm

0 引 言

作为工业生产领域的重要动力设备，由于其复杂的机械结构和恶劣的工作环境，电机内部的部件在长期运行过程中容易出现故障^[1]。常见的机械损伤主要发生在轴承、定子、转子等位置，其中轴承故障约占40%^[2]。因此掌握具有较强实用性的轴承故障诊断方法具有重大意义。

目前，振动信号分析是轴承外圈故障诊断中常用的研究方法^[]。通常情况下，振动信号分析是通过时域、频域以及计算相关的高阶特征量来进行故障的获取与判定^[4]。但由于振动信号背景干扰复杂，存在特定的缺陷，比如采样频率或轴承转速会严重干扰该方法的有效性，导致轴承外圈故障特征不明显，在应用过程中往往采用理想的近似方法，因此相应的精度较低^[5]。然而电机噪声信号具有非接触式采集、覆盖范围广、后处理大、分析空间大等优点^[6]。因此相关研究人员尝试对电机噪声信号进行检测，利用噪声信号实现故障诊断的关键是从噪声信号中提取有效特征^[7-8]。文献[9]提出一种基于声信号的单相感应电机轴承和定子故障早期诊断，分析结果良好。在电气设备故障诊断领域，声纹特征也常被用于变压器铁心松动故障的诊断。文献[10]提取的声纹特征主要与50 Hz工频信号相结合，对变压器故障诊断有很好的影响，但不适用于与工频信号弱相关的其他领域。

轴承外圈故障通常会出现噪声及电磁关系被破坏导致定子电流出现变化，电流信号的优点是直观，辨别性强^[11]。在电机的故障诊断中，通过对电流信号和声纹信号进行融合，融合信号具有更明确的相关特征，从而能够准确区分健康和故障情况。较之以往基于振动信号具有特定的优势。文献[12]提出一种基于多数据融合的电机故障诊断方法方案，研究结果表明，采用所提出的多数据融合诊断方法可以高置信度地诊断出电机的故障类型。文献[1]提出一种基于声信号和电信号融合的方法，以实现健康和不同故障情况下的新的融合信号。通过对多个传感器的输出进行加权组合以生成加权决策融合，生成融合决策。研究结果证明数据融合方案在旋转机械状态监测中的优越性。文献[14]提出电流信号深度融合的电机转速估计及轴承外圈故障诊断研究，弥补了振动信号的一些缺陷。

本文主要研究以电机工作噪声和电流进行数据融合作为电机轴承外圈故障检测依据，提出一种基于声纹特征和电流频谱的检测方法，利用小波阈值去噪算法滤除无关噪声，使故障信号特征更加突出。与经验方法得到的结果相比，基于电机噪声和电流的检测方法在测量和数据处理方面具有显著优势，能够有效地应用于轴承外圈故障诊断，又为电机轴承外圈故障诊断提供一种新思路。

1 轴承故障识别方法及检测流程

1.1 定子电流中的轴承故障特征频率

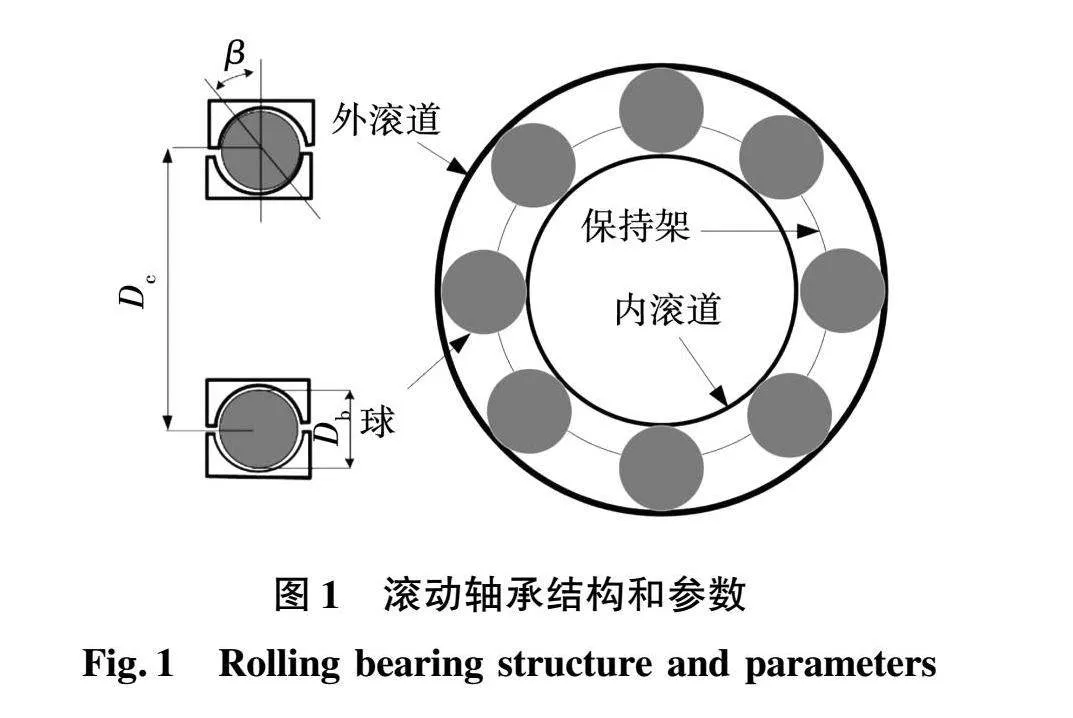
图1所示的几何形状的滚动体轴承，球的数量记为Nb，球与滚道的接触点用接触角β来表示，Db和Dc分别为球的直径和保持架的直径。

每一种轴承故障关联到一个特征频率fc，这个频率是由于故障的存在而出现异常的周期性^[15]。特征频率是轴承几何形状和机械转子频率fr的函数。对于本文所考虑的外轴承滚道缺陷，fc采用以下表达式为

f0=Nb2fr1－DbDccosβ。（1）

统计显示，大多数轴承的振动频率可以用6到12个球来近似表示^[15]为

f0=0.4Nbfr。（2）

其中在异步电机中，fr可以表示为

fr=1－spfs。（3）

其中：fs为定子电源频率；s为转差率。在轴承故障特征频率fc处发生的旋转偏心的产生，导致了电机电感的周期性变化。这将在定子电流中产生额外的频率fbf，表达式为

fbf=|fs±kfc|，k=1，2，3，…。（4）

上述模型已在大量不同的工作中得到应用，并被证明是可靠的。

1.2 气隙长度的量化

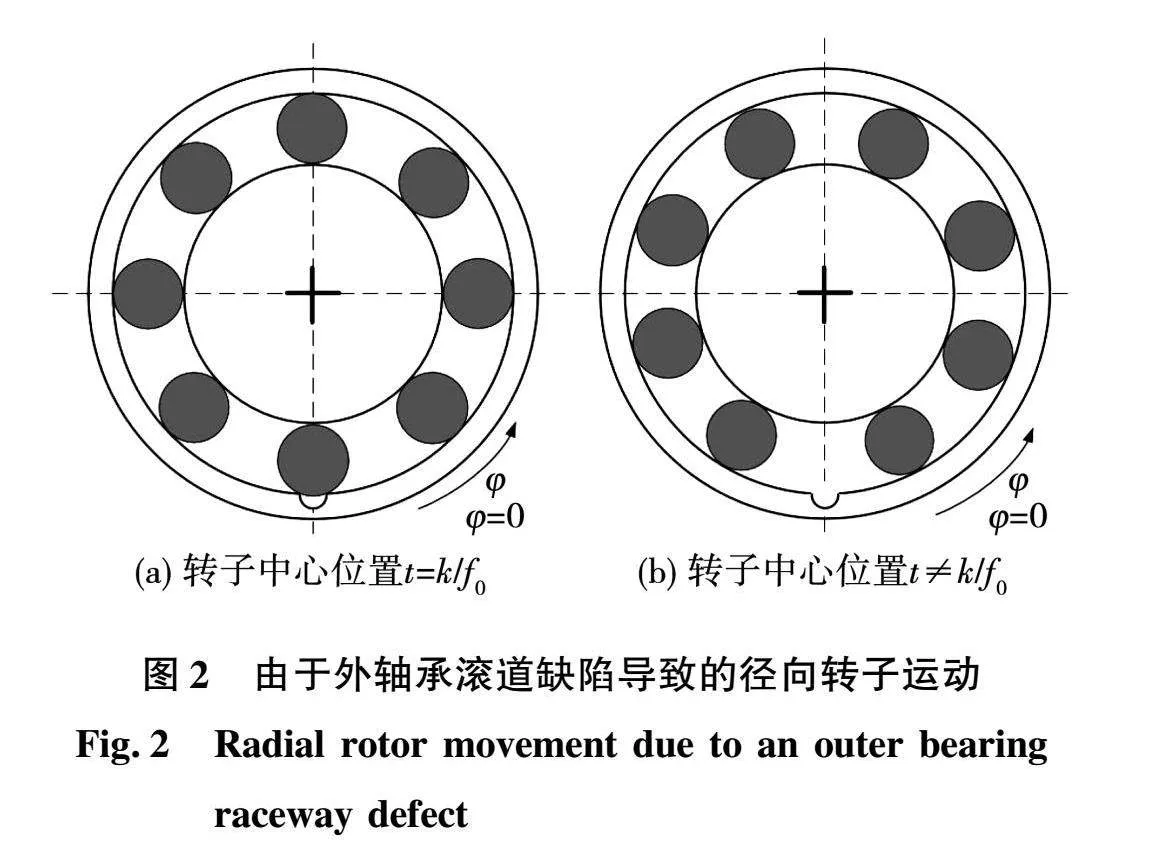
单点缺陷可以理解为相应元件上缺少一块材料。他位于滚道表面和其他元件之间。缺陷存在导致振动并增加噪音水平^[16]。为便于计算，外圈缺陷可以假设位于角位置φ=0。当没有球与缺陷接触时，转子完全居中。这种情况下，气隙长度g应取恒定值g0，忽略转子和定子开槽效应。另一方面当t=k/f0 （k为整数）时，如图2所示，球与缺陷之间的接触会导致转子在定子参考系上的中心发生小的运动。同时，气隙长度可为近似为g0（1-ecosφ），其中e是偏心性相对程度^[17]。此外，应注意，实验中的轴承类型为接触角β=0的深沟球轴承。

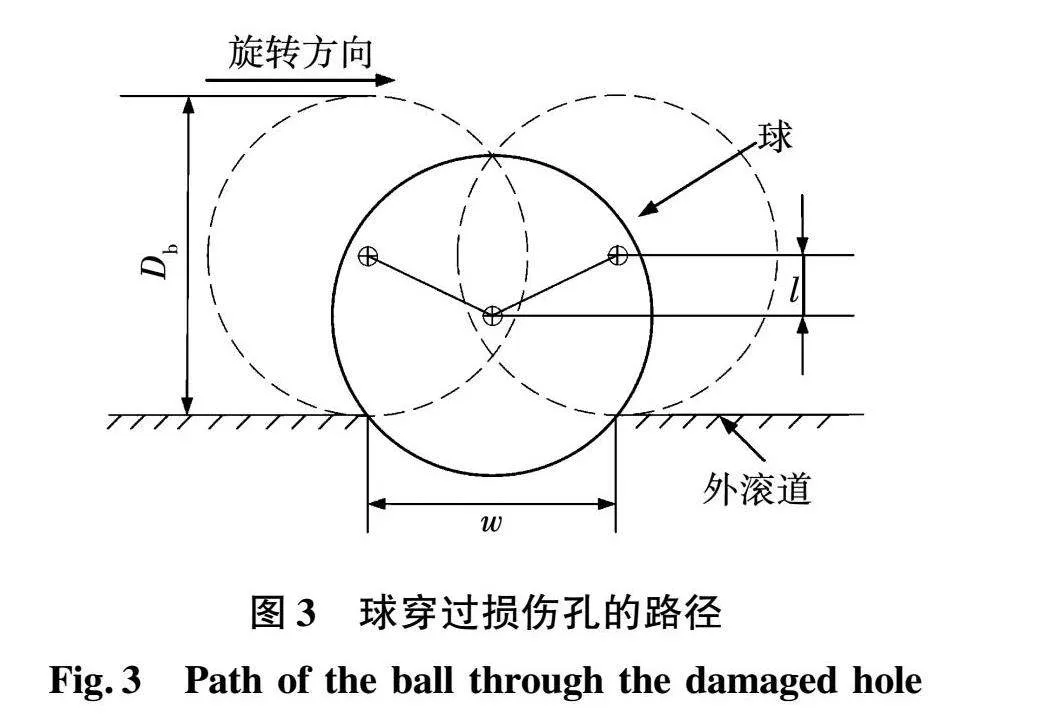
该现象是一个周期信号，类似于一个抛物线形状^[18]。图3为球通过损伤孔时球中心的近似形状（球的路径）。为便于比较和应用，将外滚道整个圆周所占的损伤孔的程度和轴承滚道上孔的宽度w所引起的偏心度e转换为无量纲化，如下式所示：

α=w2πD×100%；（5）

l=Db－D2b－（w/2）2；（6）

e=lg0×100%。（7）

式中：α为孔宽占外滚道周长的比率；l为偏心率值；D为滚道直径；Db为滚珠直径。

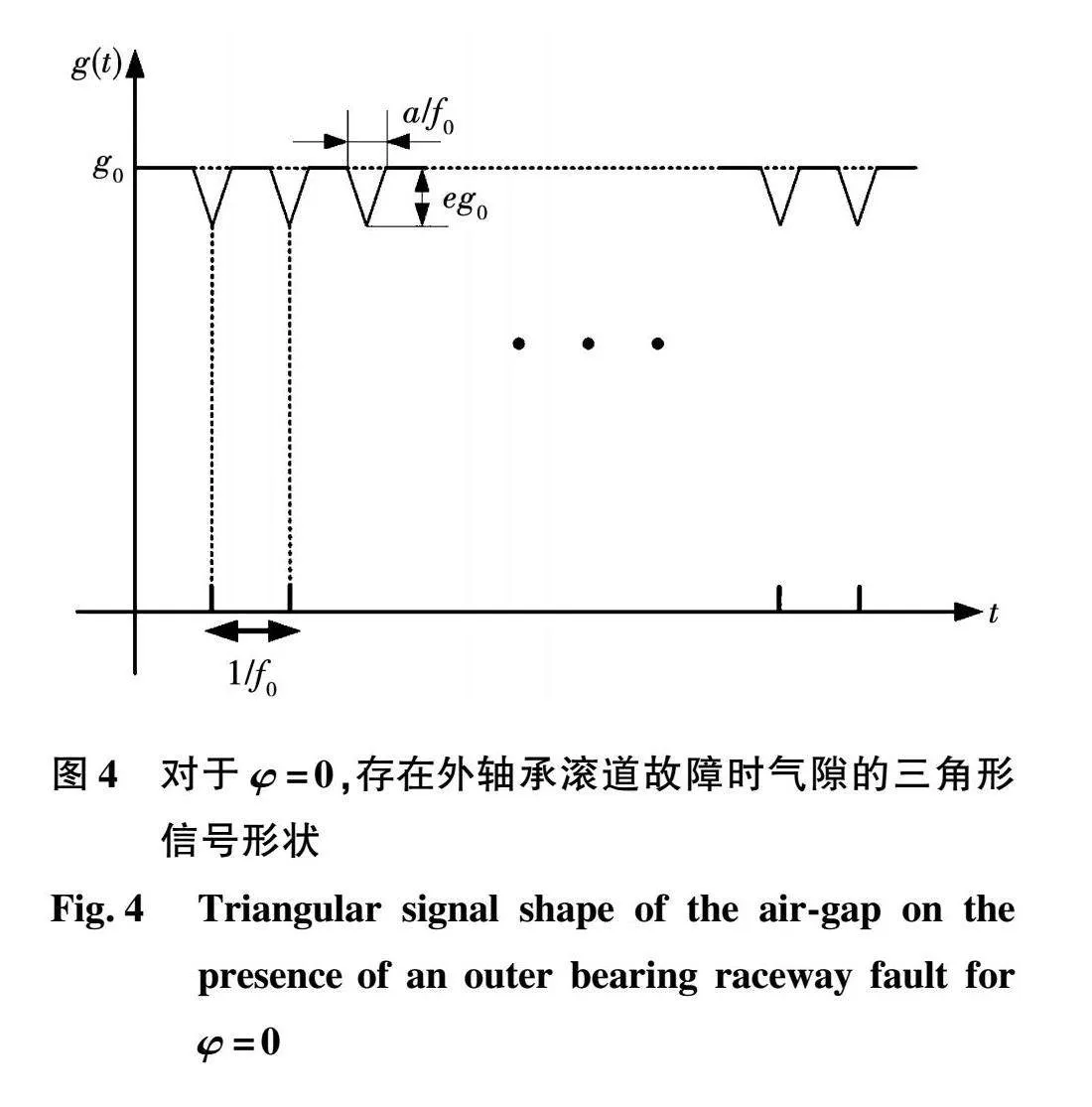
为了将外轴承滚道缺陷故障与气隙长度的关联影响建模为时间的函数，可以使用一系列三角形函数来近似描述球的路径^[18]，如图4所示。

考虑到这些因素，可以利用傅里叶级数得出如下气隙长度表达式为：

g（φ，θ）=

g01－e0cosφ2π∑+∞k=1sin（αkπ）kcos（kθ）。（8）

其中：e0是偏心的相对程度；φ是沿定子内表面的特定角位置；θ是转子相对于定子框架的角位置。

1.3 改进小波阈值去噪

小波阈值去噪通过对信号进行降阶分解，并进行多尺度信号分析。分解后得到一组小波分解系数，并设置一个临界阈值λ进行定量处理。将小于阈值λ的系数分为噪声信息和归零，这部分主要用细节成分表示信号的高频信息。当小波系数大于阈值λ时，信号的低频信息主要由近似分量表示，并认为有效信号应被保留或进一步处理。最后，通过重构处理后的小波系数，即近似分量，得到去噪信号。传统的阈值函数分为硬阈值函数和软阈值函数，硬阈值函数容易导致原始信号振荡，连续性无法保证；软阈值函数会导致去噪后信号出现方差，与原始信号出现较大差别^[19]。为了克服两者的缺点并保留优点，利用一种新的阈值函数对传统小波去噪进行改进。过程中选用Symlet6小波基，并选取固定阈值，改进的阈值函数表达式如下：

λ=σ2log10N；（9）

wλ=0，|w|lt;λ；

sing（w）|w|－λe^{1 000（|w|－λ）}，|w|≥λ。（10）

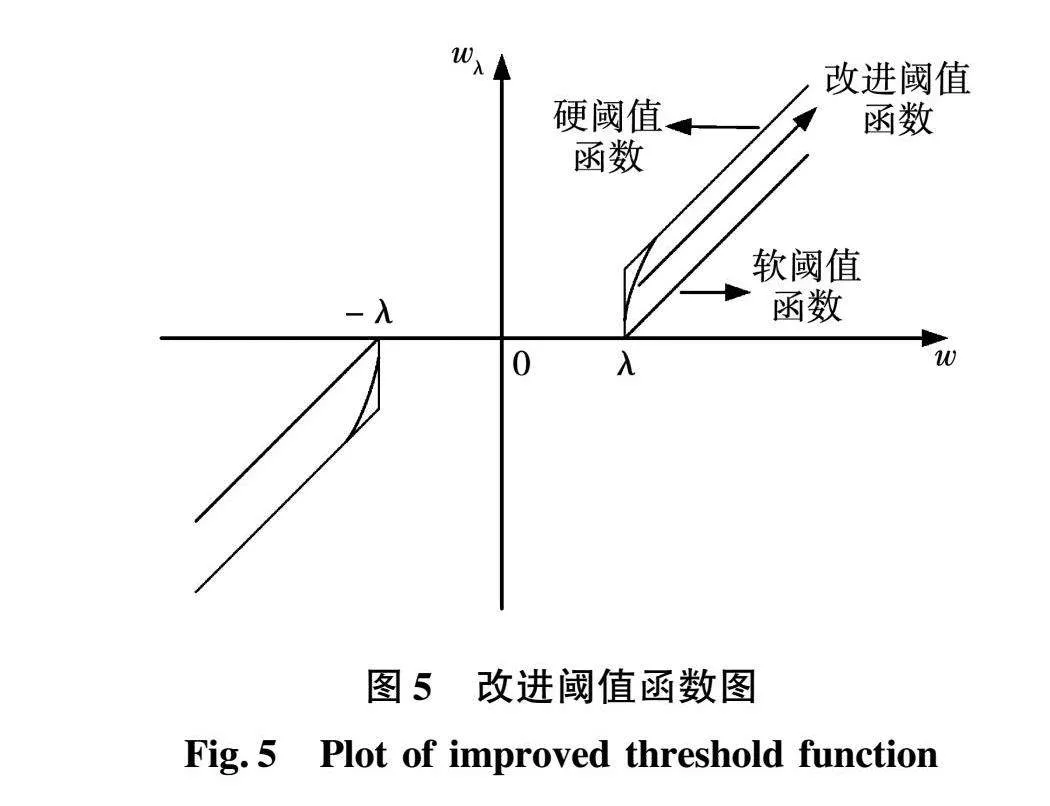
改进阈值函数如图5所示。

根据式（10）和图5分析得出改进阈值函数的优点：

1）当w=λ，wλ在阈值点左右连续，不存在硬阈值函数容易导致原始信号振荡的问题。

2）当w→∞，wλ→∞，解决了软阈值函数会导致去噪前后出现较大差别的缺点。

改进阈值函数由于在阈值点连续，并且高阶可导，较为完美的规避了传统阈值函数所带来的缺点，不仅实现阈值选取的功能，还可以表征分解后系数的能量分布，相较于传统阈值函数，信号去噪性能得到大幅度的提高。

1.4 VMD算法及其优化

变分模态分解 （variational modal decomposition，VMD） 算法通过迭代搜索变分模态的最优解，更新固有模态函数分量 （intrinsic mode functions，IMF）及其中心频率，得到特定带宽的k模态函数，实现各频段信号的分离。随后，将各IMF之和设为输入信号x（t）为约束条件，以各IMF估计带宽之和的最小值为目标^[20]。构建约束变分模型则为：

min{uk}，{wk}∑kk=1tδ（t）+jπtuk（t）e^－jwkt22，s.t.∑kk=1uk=x（t）。（11）

其中：uk表示IMF分量；wk是中心频率；t表示对t的一阶偏导数。

通过引入二次惩罚因子α和拉格朗日惩罚算子λ（t），将约束变分问题转化为非约束变分问题，即

L（{uk}，{wk}，λ）=α∑kk=1tδ（t）+jπtuk（t）e^－jwkt22+

x（t）－∑kk=1uk（t）22+

〈λ（t），x（t）－∑kk=1uk（t）〉。（12）

其中：α为二次惩罚因子；λ（t）为拉格朗日惩罚算子。利用交替方向乘子法（alternating direction method of multipliers，ADMM）求解式（12）的最优解。将unk、wnk、λn和迭代数n的初值设为0，并通过迭代更新得到模型的合适解，即：

u^ⁿ⁺¹k（w）=x（w）－∑ki≠ku^k（w）+λ^（w）/21+2α（w－wk）2；（13）

wⁿ⁺¹k=∫∞0w|u^k（w）|2dw∫∞0|u^k（w）|2dw；（14）

λⁿ⁺¹（w）=λn（w）+τx（w）－∑kk=1uⁿ⁺¹k（w）。（15）

其中τ表示噪声容忍参数，通常取τ=1×10^-7。当满足SymboleC@kk=1‖uⁿ⁺¹k-unk‖22/‖unk‖22＜ε时，迭代停止。最后，通过傅里叶反变换可得到时域uk。

VMD算法中分解模态数k的数值选取对信号处理结果有着较大的影响，分解模态数k的大小对应不同的信号分解性能。由于VMD方法分解出的IMF分量数k具有很大的随机性，为了选择合适的k值，采用文献[21]中的鲸鱼算法 （whale optimization algorithm，WOA） 自适应地选择VMD模型的k值。因此，在信号分解时可以利用其进行参数选取，从而提高信号分解精度。此算法是根据鲸鱼的捕食行为而来，算法对座头鲸的狩猎行为进行模仿，通过对猎物的寻找，而进行攻击，以此来达到优化的目的。

1.5 MEL谱原理与提取

通过以上步骤，得到k个IMF分量，从频谱中分析每个分量的中心频率，选择Q个IMF分量重构信号。重构后的信号x（n）表示为

x（n）=∑Qk=1uk（n）。（16）

对重构信号x（n）执行分帧和加窗操作。分帧后的信号设为s（n），其中n=1，…，N-1，N为帧长度。默认增加Hann窗口h（n），加窗后的信号x[n]表示为

x［n］=s（n）h（n）。（17）

对每一帧信号进行离散傅里叶变换（DCT），计算出每一帧的功率谱P[k]为：

X［k］=∑N-1n=0x［n］e^－j2πNnk，k=0，1，2，…，N-1；（18）

P［k］=|X［k］|2。（19）

其中x[n]表示通过成帧和加窗获得的离散音频序列的帧。X[k]表示N个点的复级数，然后取X[k]的模平方得到信号的功率谱P[k]。将功率谱P[k]输入Mel滤波器组Hm[k]，在频域对冗余信号进行化简，对功率谱进行对数运算得到Mel谱^[22]。Mel频率与频率之间的关系和Mel滤波器组^[2]如下：

Mel（f）=2 595log101+f100；（20）

Hm（k）=0，klt;f（m－1）；

k－f（m－1）f（m）－f（m－1），f（m－1）≤k≤f（m）；

f（m+1）－kf（m+1）－f（m），f（m）≤k≤f（m+1）；

0，kgt;f（m+1）。（21）

S（m）=log10∑Mm=0|X（k）|2Hm（k），0≤m≤M。（22）

式中f（m）为Mel滤波器的中心频率，定义为

f（m）=12（fh－fl）fh+flfh－fl2－1。（23）

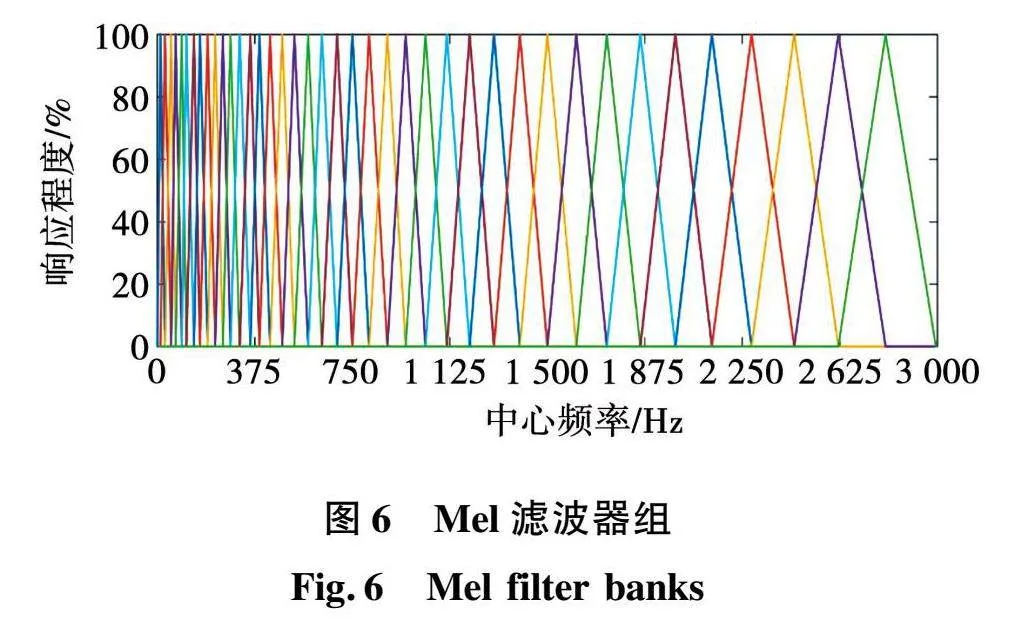
当m∈[1，m]，m与f（m）正相关，m表示三角滤波器个数。其中Mel滤波器组如图6所示，三角滤波器的特性可以从帧信号的较低频率的波段获得更多的声纹信息，并在帧信号的高频波段进行压缩。

梅尔频率倒谱系数 （Mel-frequency cepstral coefficient，MFCC）特征是说话人识别研究中常用的声纹特征之一。MFCC特征向量相关性低，适用于传统分类模型，而Mel谱更适用于神经网络模型^[24-25]。原始音频信号的Mel谱不仅包含轴承的工作状态信息，还包含大量的白噪声信息，降低了特征提取的效率。

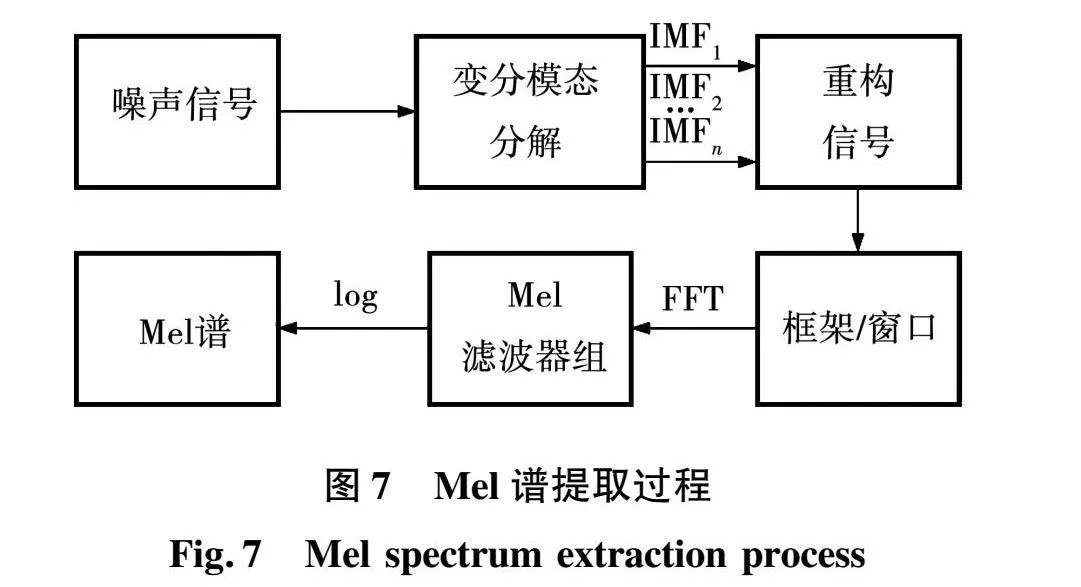
为了解决这一问题，采用变分模态分解方法将音频分解为多个IMF分量，观察IMF的中心频率，选取几个IMF分量重构无大量白噪声的电机轴承噪声信号。改进的Mel声谱特征提取过程如图7所示。

通过以上特征提取步骤，可以有效滤除白噪声的影响，降低白噪声干扰。可以根据需要调整正则化系数，从而控制分解结果的稀疏性和光滑性。得到给定信号的有效分解成分，最终获得变分问题的最优解。

2 Mel-CNN融合电流模型理论

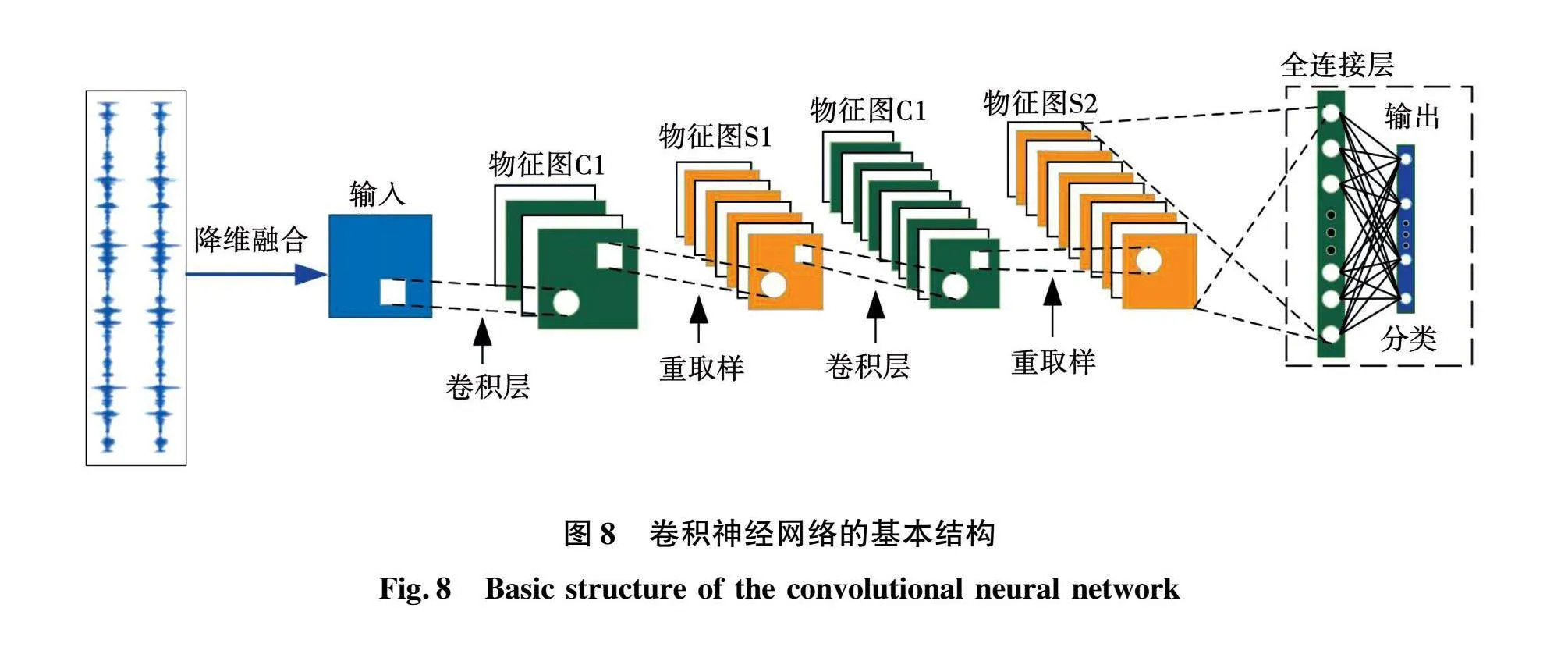
此次融合神经网络模型由卷积神经网络 （convolutional neural network， CNN） 和长短期记忆网络（long short-term memory network，LSTM）串联融合而成，即CNN-LSTM。由于神经网络数据拟合能力强，不仅可以提取传统拓扑结构特征，还能提取高维特征。通过增加一个网络层来提取更鲁棒的特征来表示输入样本^[26]。图8为卷积神经网络的基本结构，其中激活函数选择为修正线性单元（rectified linear unit，ReLU），收敛速度快。池化层选择为最大池化，具有很好的平移不变性，减小了卷积运算后特征图的维数，提高了网络计算速度^[27]。LSTM可以克服递归神经网络中梯度消失问题，在时间序列数据分析中具有优势，是一种有效的时间序列预测工具。LSTM网络包括3个门：遗忘门、输入门和输出门。这3个“门”连接在一起，决定存储或忘记哪些信息。LSTM的关键部分是单元格状态，通过生长函数和正切函数来选择信息。其网络体系结构如图所示。本文通过Matlab对LSTM算法进行了计算，并通过4种降维技术，即局部切线空间对齐（local tangent space alignment，LTSA）、局部线性嵌入（locally linear embedding，LLE）、主成分分析（principal component analysis，PCA）、独立成分分析（independent component analysis，ICA） 将高维特征转化为低维特征，保持原始数据的内在几何性质。这些技术的优点是在不丢失有用信息的情况下，通过融合高维原始特征来提取有用的低维特征。根据样本集的大小和Mel谱的特点，设计合适的CNN来处理电机外轴承滚道故障噪声的声纹特征。在基于CNN的轴承故障诊断模型中，提取的声纹特征以二维矩阵的形式呈现，矩阵中的每个元素表示故障噪声信号的能谱密度。利用输入层，将融合电流特征的声纹特征样本输入到包含轴承故障传统声学特征的网络结构中。利用卷积二维卷积层，提取传统声学特征以外的高维特征和难以描述的特征。

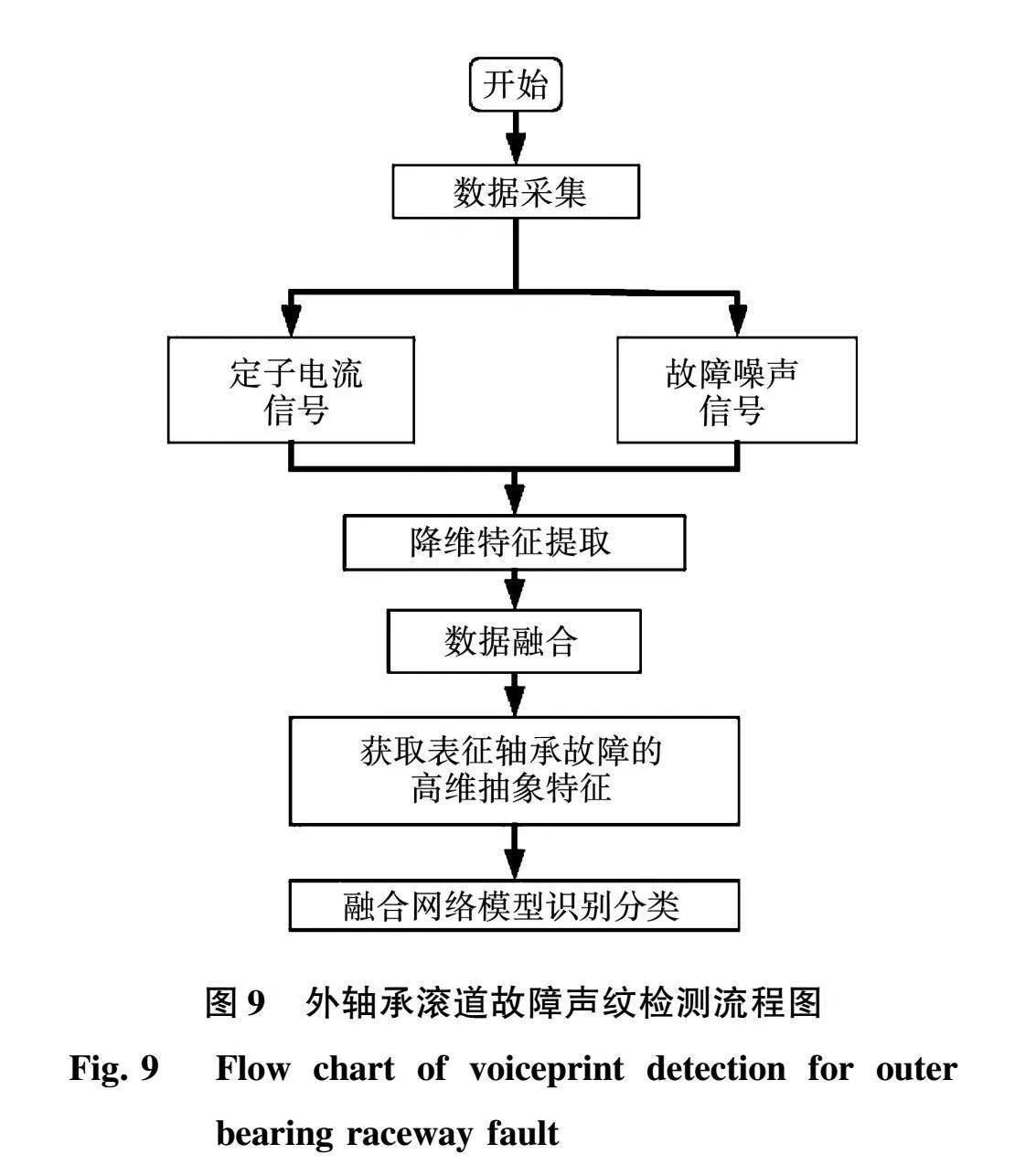
为了深入研究，本研究在故障电机实验平台上测量了外轴承滚道故障作用下的电流信号以及噪声信号。实验流程如图9所示。

3实验装置与结果分析

3.1 实验装置基本参数

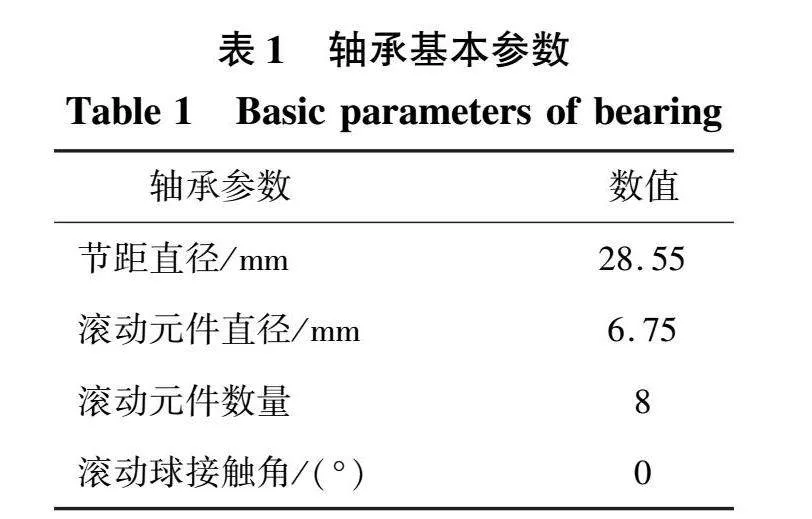
实验平台主要由本次实验装置由图10所示，由感应电机、PC端、信号采集分析仪、示波器、变频器等装置构成。本次实验所采用的轴承型号为6203，内径为24.0 mm，外径为33.1 mm，如图11所示。采用轴承具体参数如表1所示。

噪声采样频率为44.1 kHz，额定转速固定为1 500 r/min。电机电流的采样频率为64 kHz。如图11所示为外圈雕刻的故障轴承，采用人工雕刻损坏，对轴承的外圈加工钻孔，模拟外滚道故障。在本次实验中，收集了2组轴承噪声信号，包括正常轴承（Nor）、外圈裂纹（Out），以作对比。提取Mel谱特征并融合电流特征作为CNN模型的样本集。针对Mel谱特征建立合适的CNN模型，最后利用训练后的模型进行轴承外圈故障类型识别。

3.2 外圈轴承故障对定子电流的影响

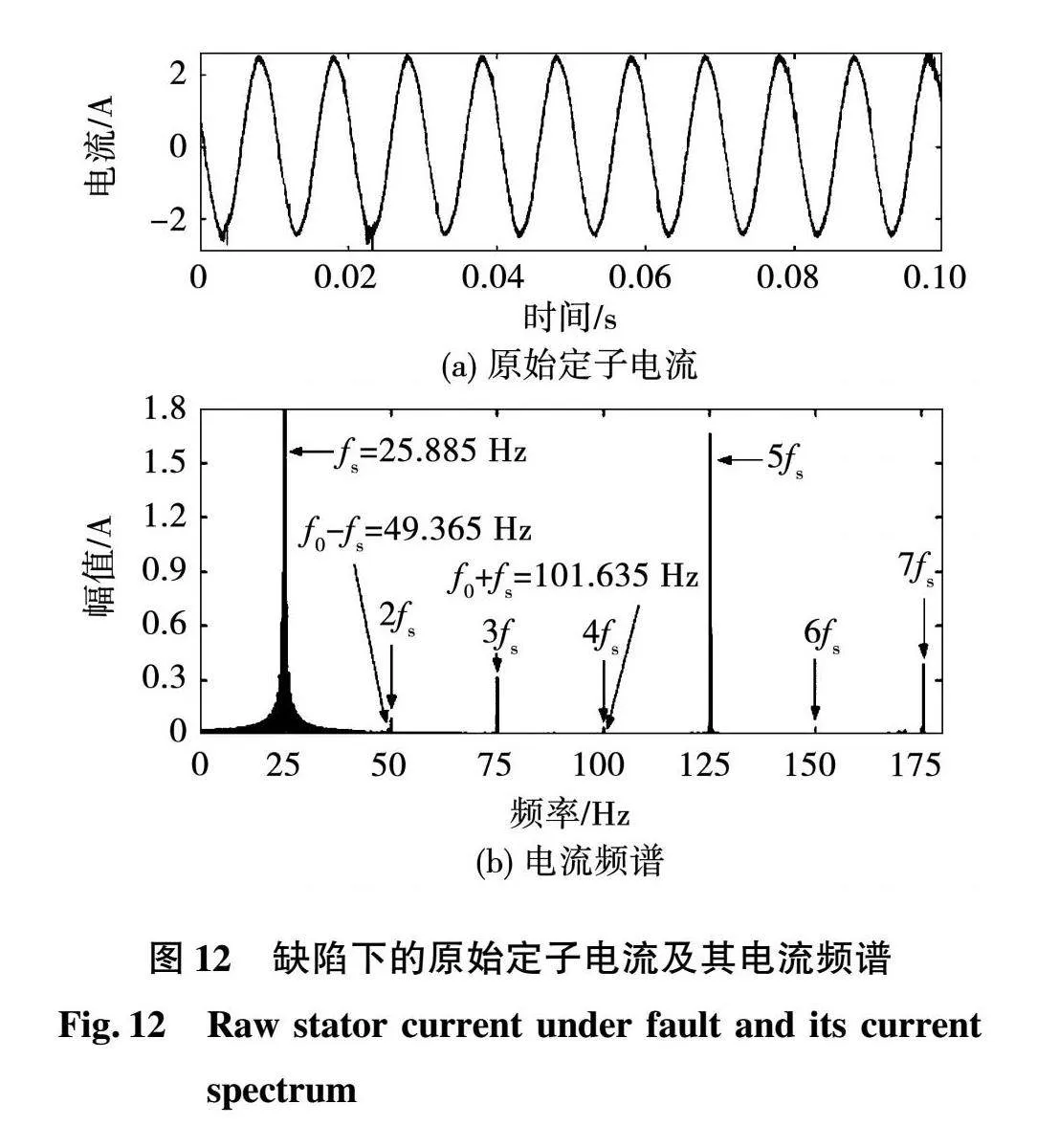
将定子电流作为异步电机轴承外圈故障检测依据。电源频率为fs=25.885 Hz，转速为1 500 r/min，则fr=25 Hz。根据式（1）和表1参数，预计观测到f0=3.06fr=76.5 Hz。图12显示了外滚道缺陷下的原始定子电流及其电流频谱。

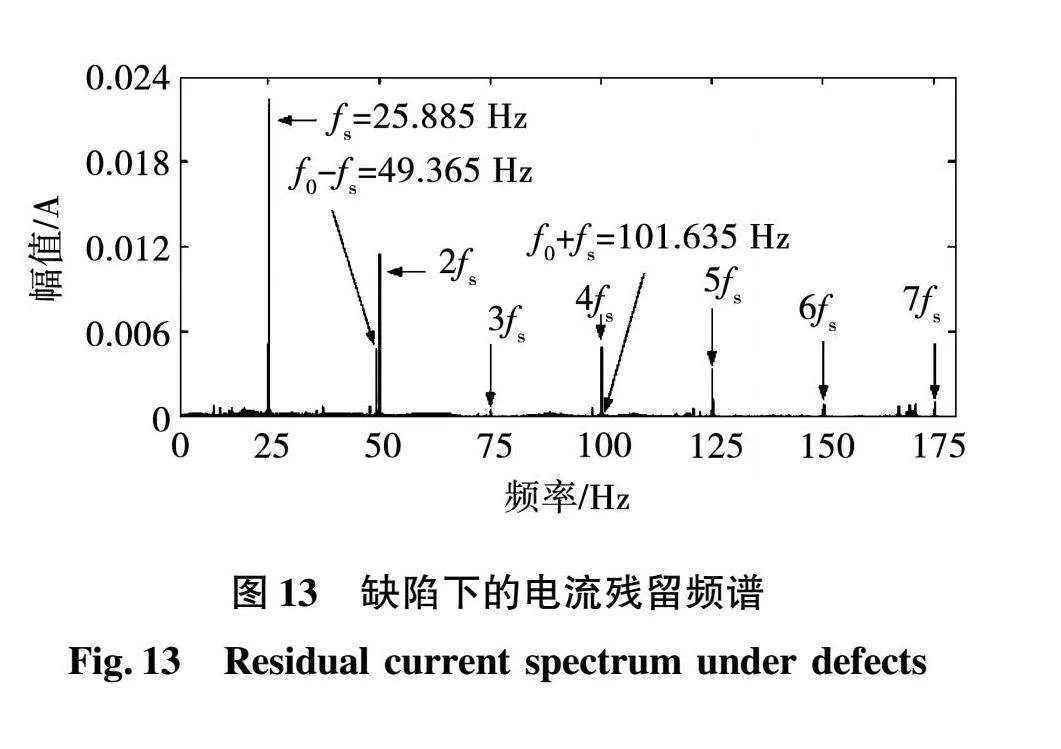
原始电流谱中的主要成分是基波与其倍数倍频。从图中可以看出，故障信号f0-fs、f0+fs并不明显。采用上文所提出的改进的小波阈值去噪模型，将电流噪声消除，噪声分量的大小显著降低，得到外滚道缺陷下的电流残留谱如图13所示，目的是消除基本倍数及其奇倍数。缺陷特征f0-fs可以变得明显，相较于图12，外圈故障特征频率较为明显。

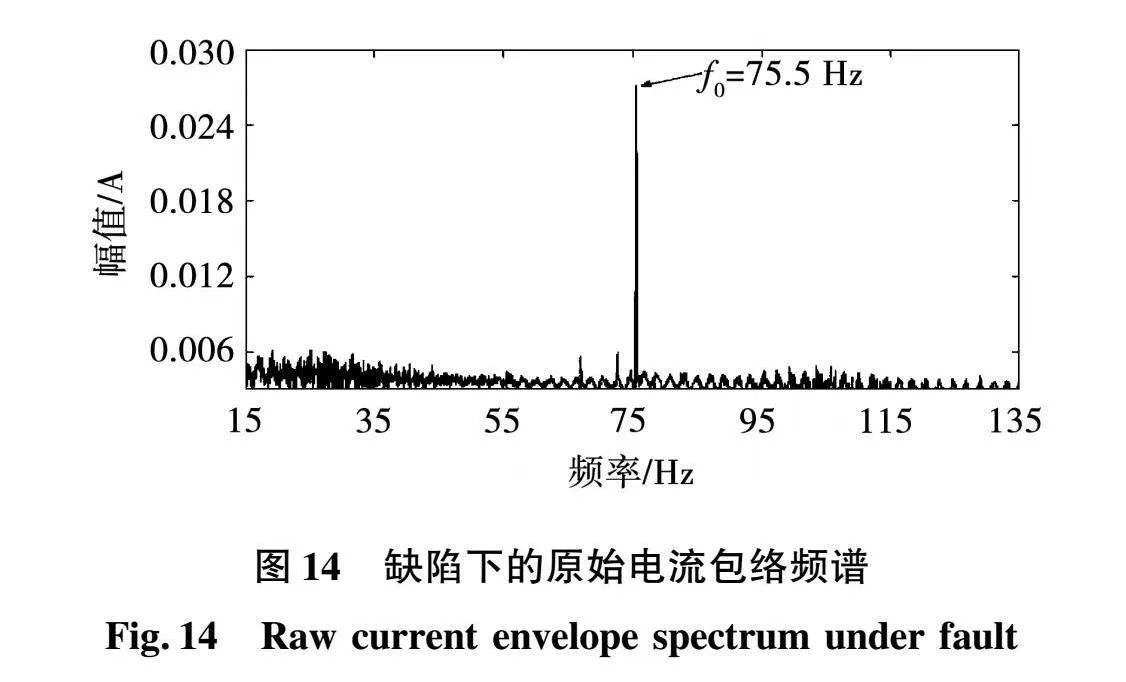
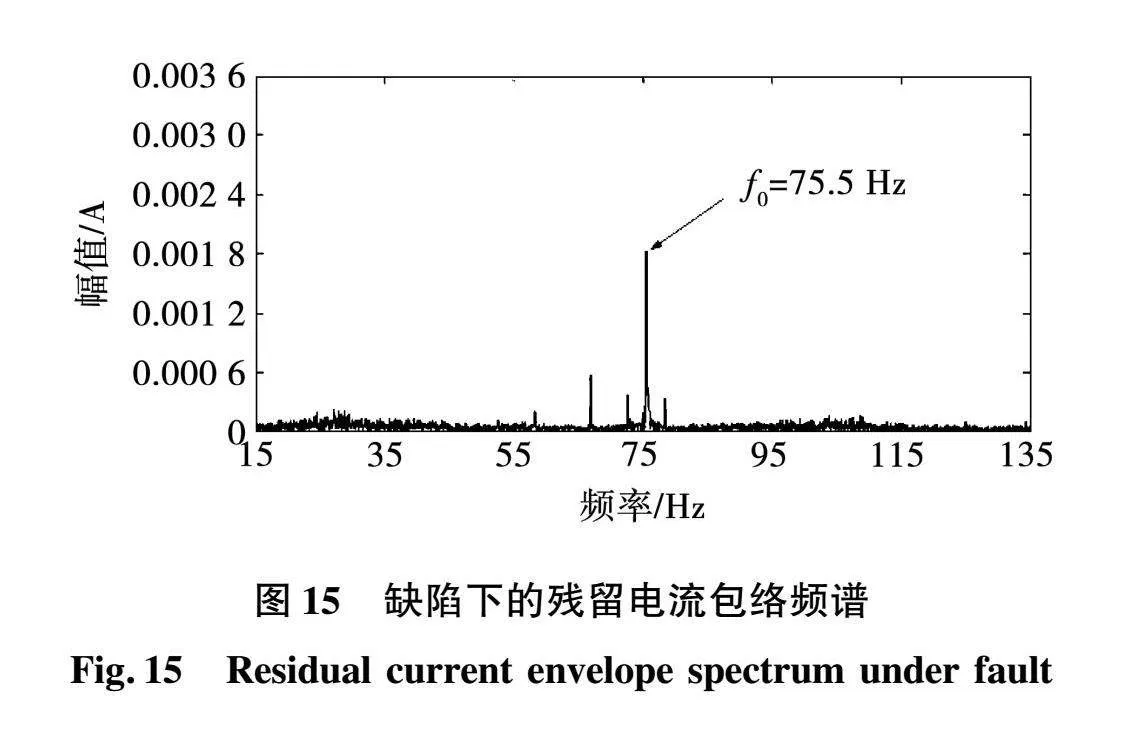
通过包络谱分析法可以把与故障频率有关的信号从高频调制信号中解调出来，以此降低其他低频干扰的混淆，对比来说可以提高诊断准确率和灵敏度。外滚道缺陷下的原始电流和电流残留信号的包络谱分别如图14和图15所示。

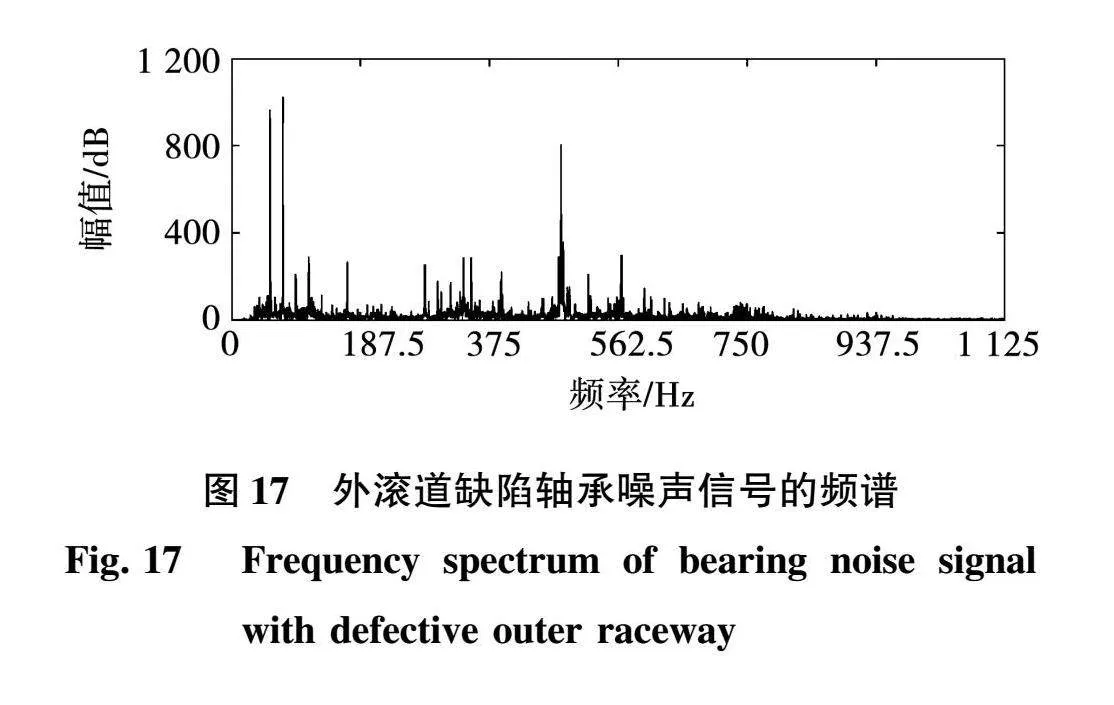
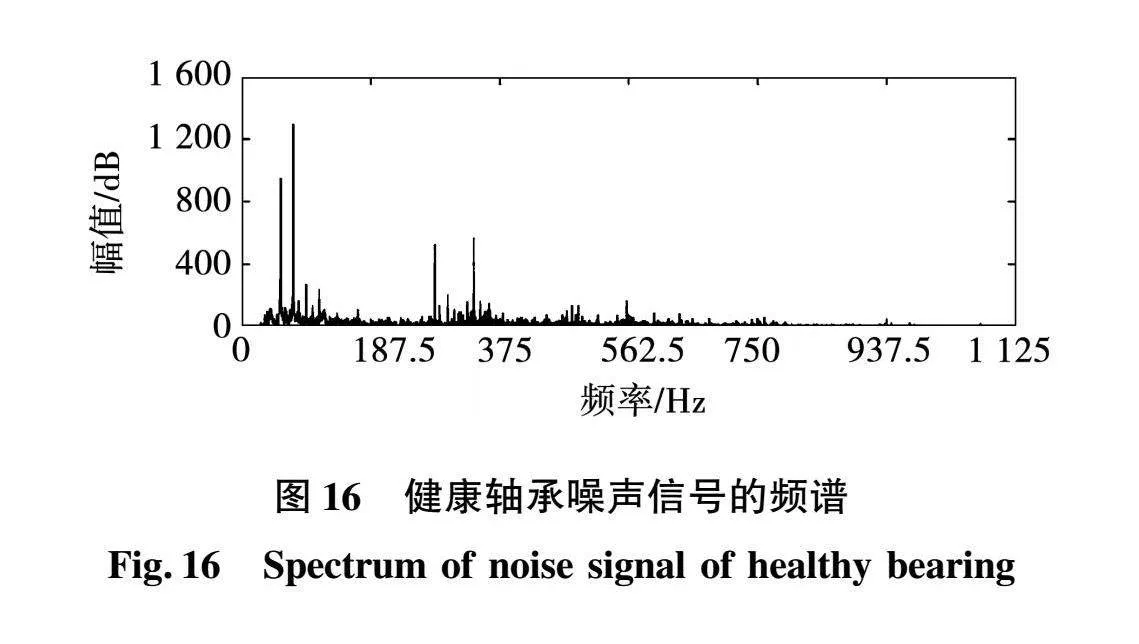
图中观测到的故障频率为75.5 Hz，与传统计算得到的外滚道故障频率非常接近。证明电流频谱判断故障发生的可行性较强，判断准确率高。安静条件下，通过采集仪器收集故障轴承的运行噪声信号，并根据电机噪声进行了背景噪声的修正。如图16、图17所示为健康状态轴承与外滚道故障状态轴承噪声信号频谱。

结果表明，故障特征谱差异明显，噪声谱主要分布在0～1 125 Hz范围内。健康轴承噪声频谱分布在0～500 Hz的频率区间，主要集中在75～150 Hz和260～340 Hz。外滚道缺陷故障轴承噪声频谱的显著分量集中在0～180 Hz、200～375 Hz及470～650 Hz的频率区间。通过轴承在不同状态下的噪声频率，可以得出轴承故障对电机噪声有显著影响，即噪声信号可以作为诊断电机轴承故障的样本信息。

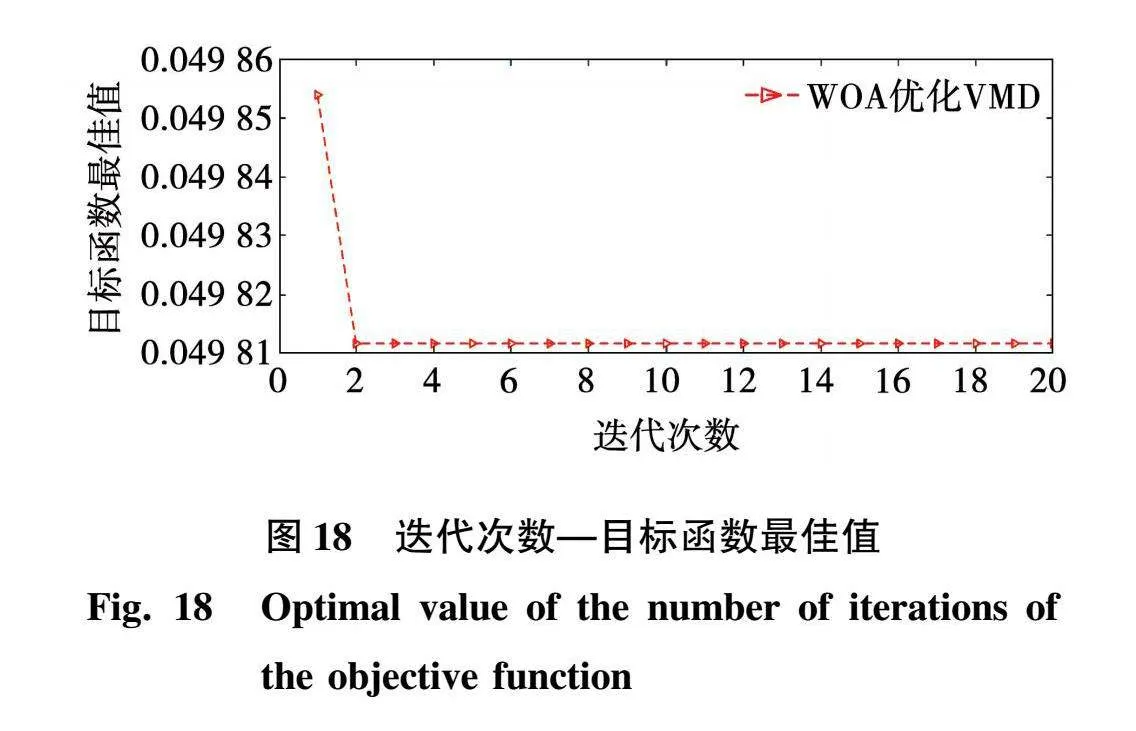
通过对比图16、图17的健康轴承噪声信号以及外滚道缺陷轴承噪声信号的频谱，电机运行时的噪声中存在许多高频白噪声，这在一定程度上影响了模型的识别结果。因此，利用VMD方法对噪声信号中的高频和低频成分进行分解和重构。通过剔除高频成分，可以达到消除白噪声的目的。据上文所述，以外滚道缺陷轴承噪声信号数据为例，采用鲸鱼算法对VMD算法进行优化，可以对IMF分量及其对应的频谱进行自适应分解，以最小样本熵作为适应度函数进行寻优，整体误差较小，迭代计算结果较为精确。如图18所示为随着迭代次数增加，目标函数最佳值变化图。

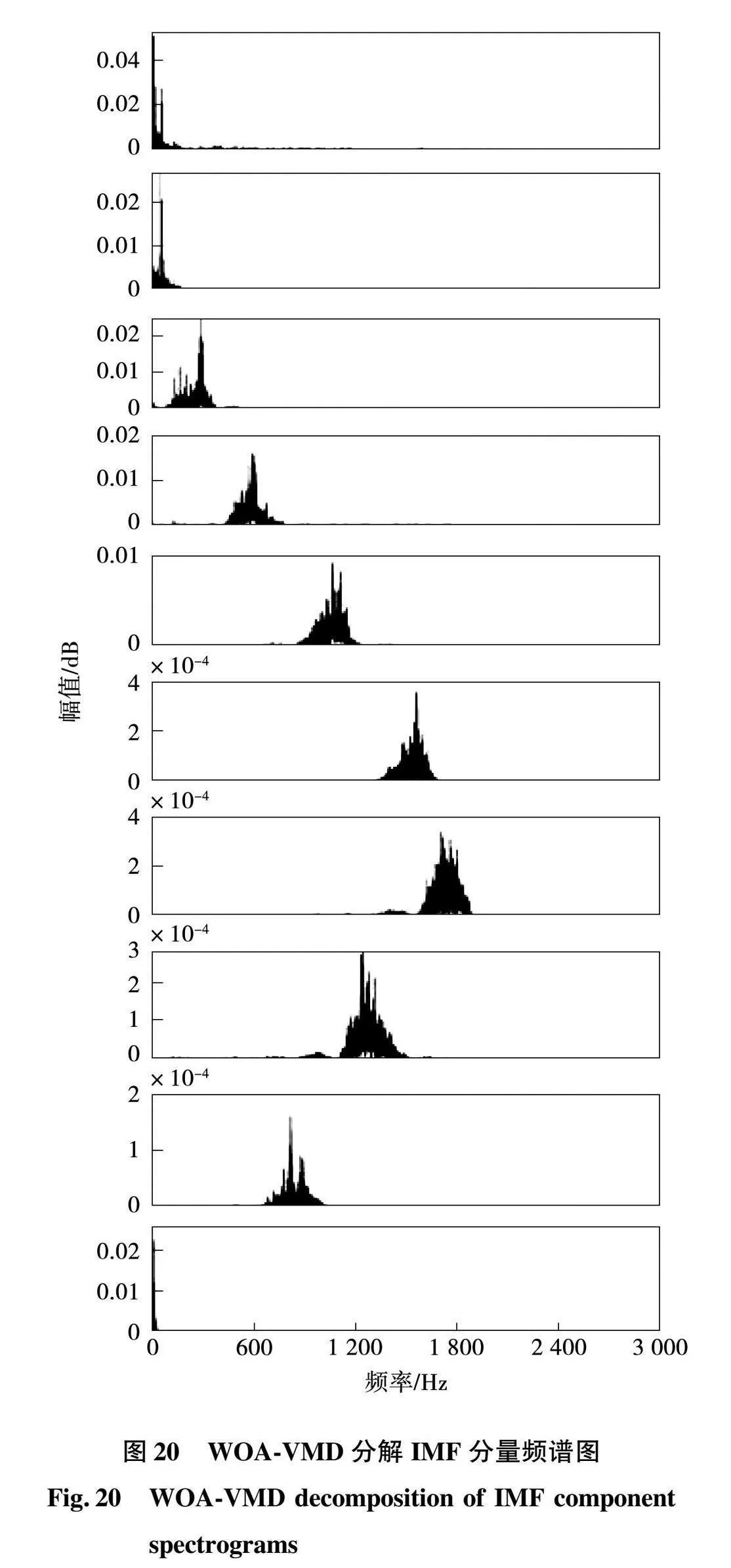
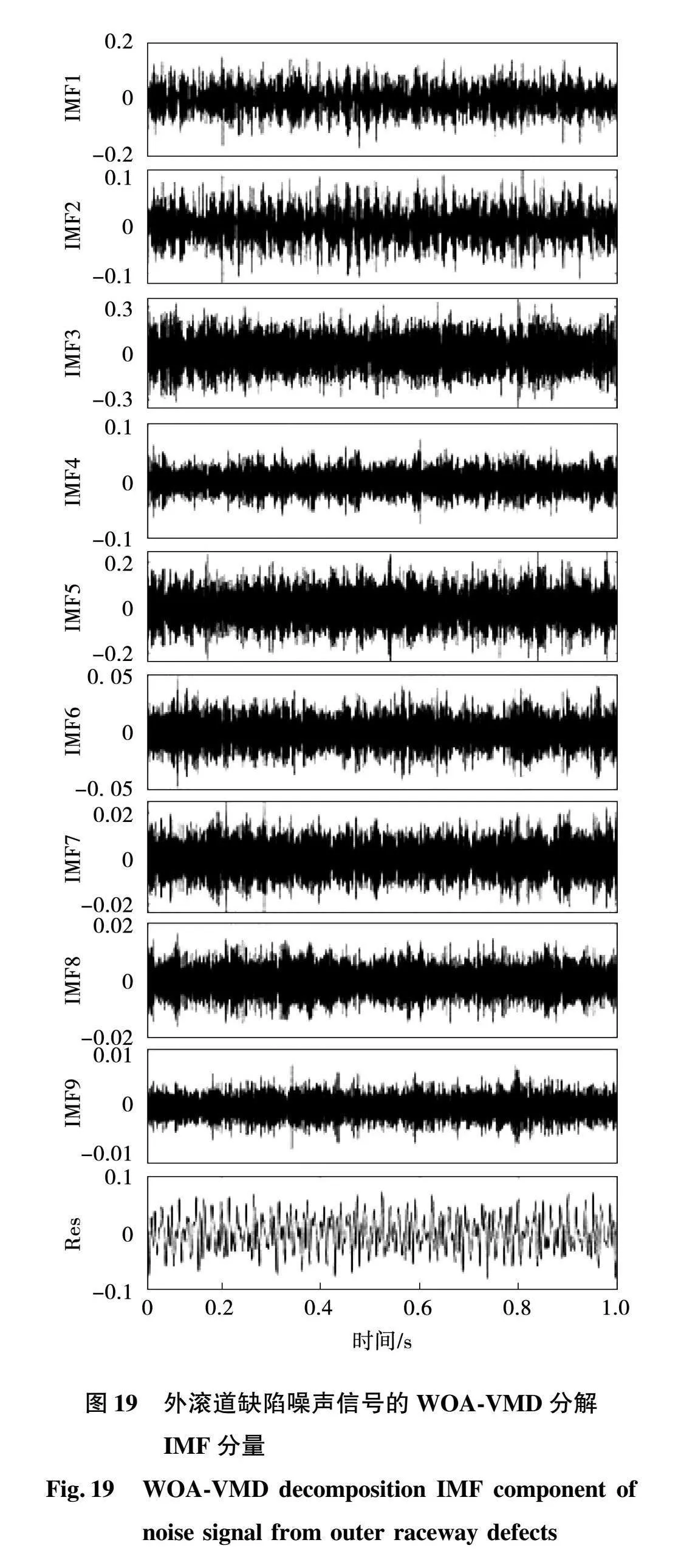
变分模态分解能够将信号分解成多个单分量信号，构造求解约束变分问题，将原始信号分解为指定个数的IMF分量，从而实现信号的频域剖分及各分量的有效分离，使得故障信号特征更加明显。由图18可知，目标函数最佳值，即最小样本熵为0.049 811，则此时样本信号数据自我相似度高，有利于信号分解，且此时最佳模态分解分量k=10。设置模态分解量为10，如图19、图20所示为对噪声信号进行自适应分解及模态分量的频谱图。

通过模态分解，可以得到各分量，各分量的幅值存在较大区别，说明存在一定的高频白噪声干扰，在进行信号传输时，对有效信号干扰严重，影响信号精度。对模型的识别结果有一定的影响。

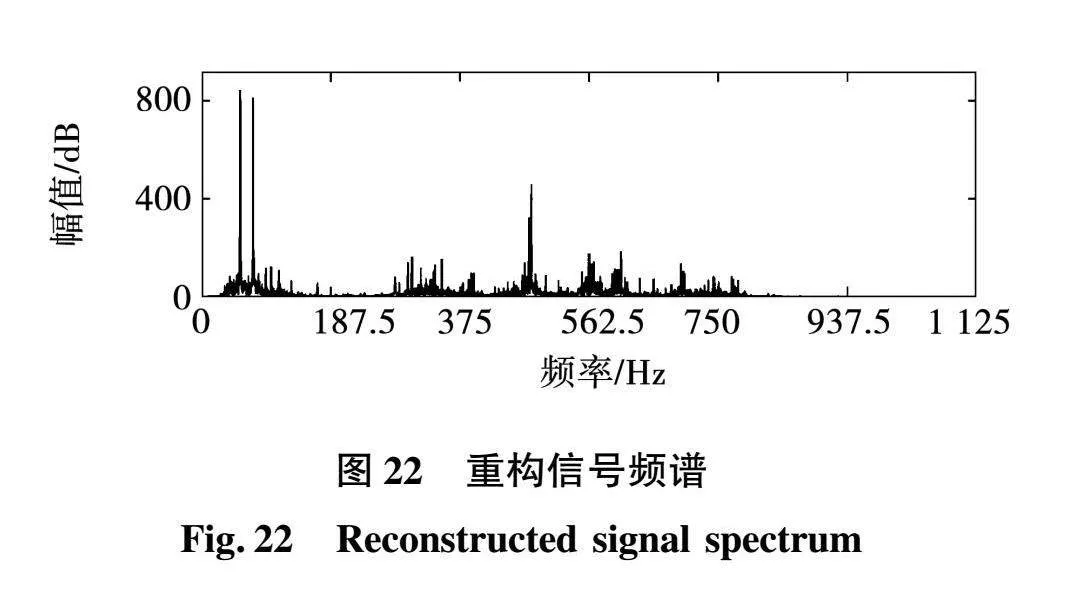
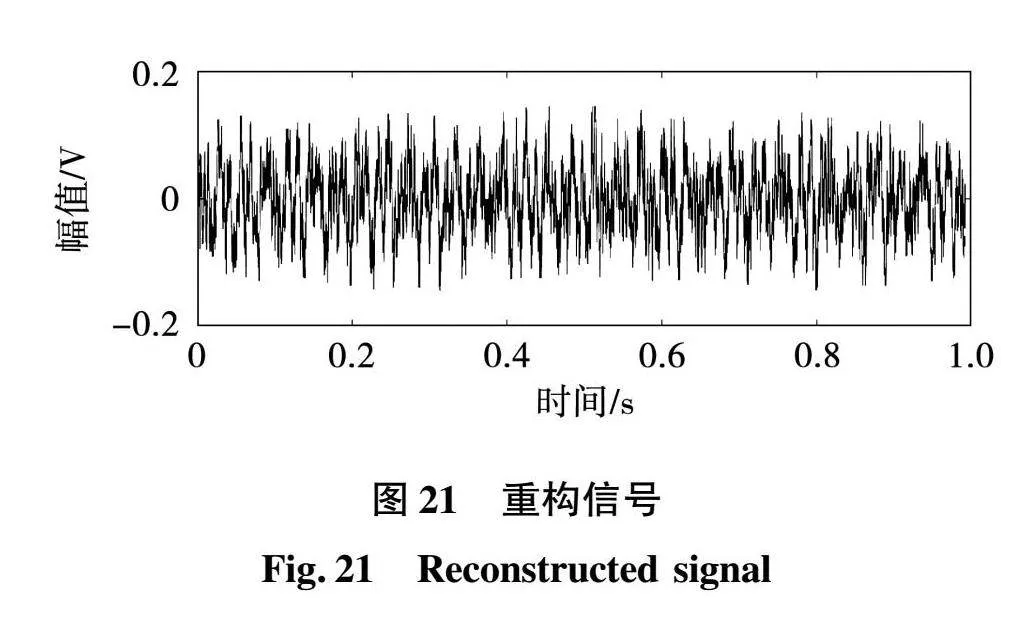
根据各分量的频谱图，可以检测到各分量之间没有明显的频谱混叠。第6个IMF的高频分量的振幅显著减小。这意味着第6～10个IMF分量可以看作是高频白噪声信号。选取前5个IMF分量重构电机噪声信号。以输出噪声信号为例，其重构信号及其频谱如图21、图22所示。

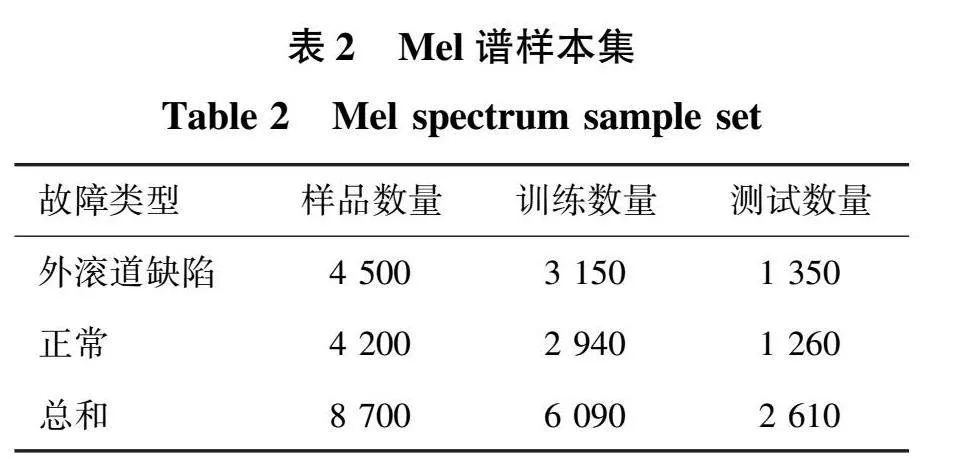
由图17和图22可知，轴承故障的噪声频率基本集中在0～750 Hz范围内。进一步降低噪声采样频率，减小数据的尺度。计算结果表明，电机的额定转速为1 500 r/min，考虑轴承故障噪声周期，电机旋转一个周期约有695个采样点。在提取声纹特征时，保证每个采样帧至少包含一个采样周期，因此帧长为采样周期的2倍，1 390个采样点，即80 ms。Mel谱的特征尺寸为128×63，其中128为特征维数，63为每个音频样本提取的特征帧数。

实验采用的Mel谱样本集的规模如表2所示。样本数量充足，通过可视化轴承故障噪声的Mel谱特征，观察到同一频率下不同状态下轴承噪声的能量差异。从Mel谱能量的全局分析来看，Mel谱对各种故障类型的轴承噪声的识别程度较高。通过优化算法降低了高频白噪声的影响，突出了轴承低频噪声的差异，增强Mel谱特征提取的能力，提高模型识别的准确性。

3.3 Mel-CNN融合电流模型故障声纹识别结果

为了保证提取高维特征时的效率，并保留卷积层的边缘数据。为此，卷积操作的填充类型选择为“相同”。通过批量归一化操作可以对输入样本进行归一化，减少了计算量，提高了神经网络的稳定性。此外，全局最大池化操作将转换的2D数据，传递给下一个全连接层。为了防止过拟合，网络中的2个全连接层进行了防止过拟合操作，防止过拟合值设为0.5。利用全连接层，通过分类函数（Softmax）将网络学习到的特征适当地映射到样本的标签空间。标签空间由2个神经元组成，分别代表2种不同的轴承状态类型。通过上述过程，我们可以实现电机轴承故障的分类和识别。实验过程中采用的CNN的结构如表3所示。

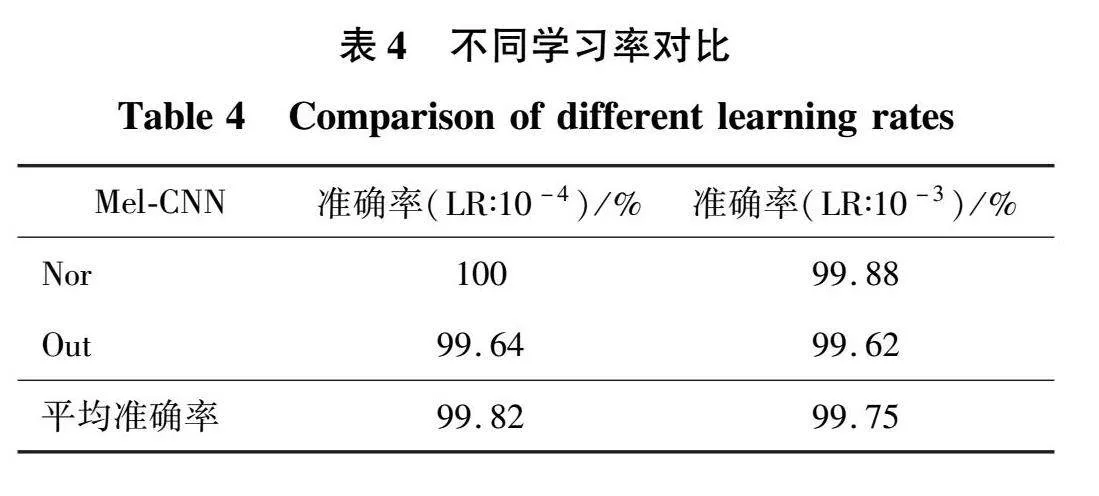
选择稀疏分类交叉熵作为CNN模型的损失函数。批量梯度下降大小和训练周期分别为32和100。并进行动量优化器，有利于梯度更新。收敛学习率的选择也会影响模型的训练效果，学习率越大，模型的收敛速度越快。根据以往大量训练经验，学习率（LR）一般设置为10^-3或者10^-4较好。表4为当学习率设置为10^-3和10^-4时，经过100个训练周期后对外滚道缺陷轴承故障的识别准确率。

由表4可知，经过100个训练周期后，当模型学习率为10^-4时，Out的识别准确率约为99.64%，Nor的识别准确率约为100%。当模型学习率为10^-3时，Out的识别准确率约为99.62%，Nor的识别准确率约为99.88%。从2种状态下的识别准确率来看，模型学习率为10^-4具有更高的准确性。由此可见，基于Mel-CNN的在轴承故障识别分类模型中是可行的。

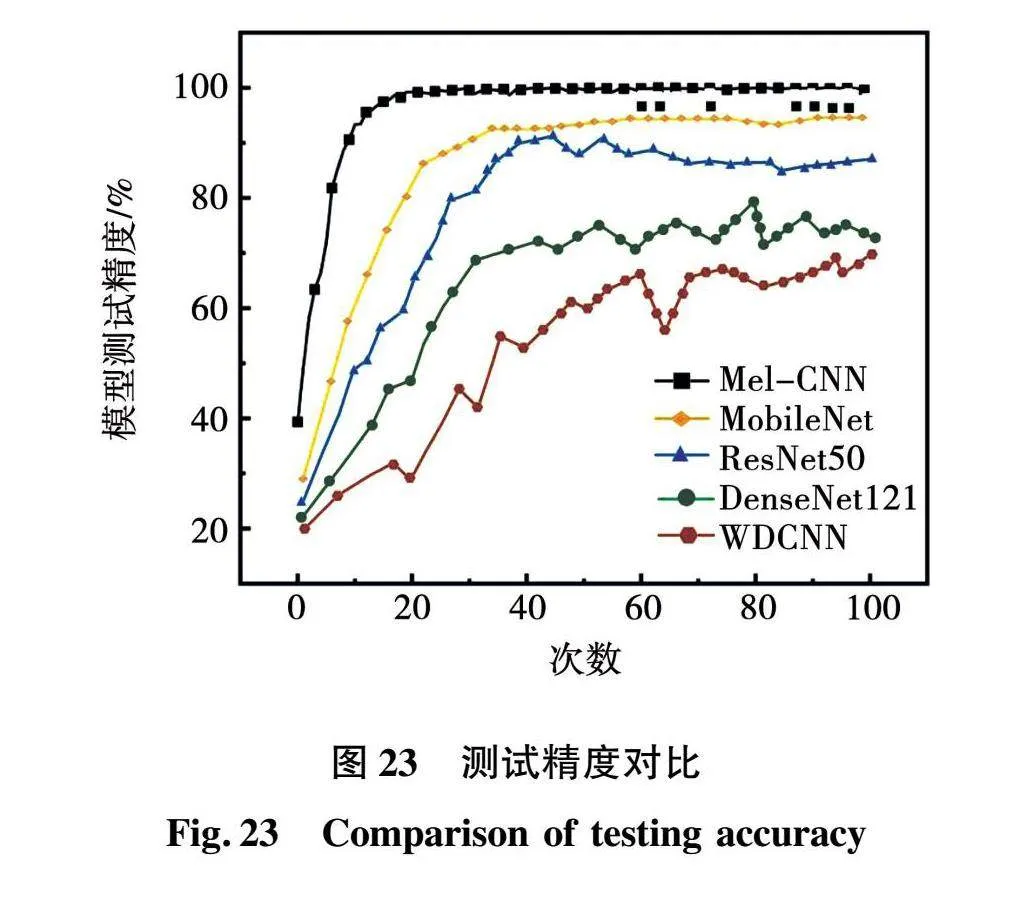
为了验证模型性能，利用常用的单一声纹神经网络模型进行实验对比，即移动神经网络（mobile network， MobileNet）、密集连接卷积网络（densely connected convolutional network 121，DenseNet121）、自联想神经网络（weighted deep convolutional neural network，WDCNN）、残差网络（residual network 50，ResNet50）。所有的模型输入为采集生成Mel谱样本集。模型测试的精度结果如图23所示。

从图23所示的模型精度对比可以看出，声纹网络模型DenseNet121、WDCNN、ResNet50的测试精度较低，模型测试并不稳定，出现波动现象。MobileNet声纹模型的最终测试准确率较高，均接近100%，但Mel-CNN融合电流模型测试准确率较高，达到稳定经历的迭代次数较少，性能最佳。

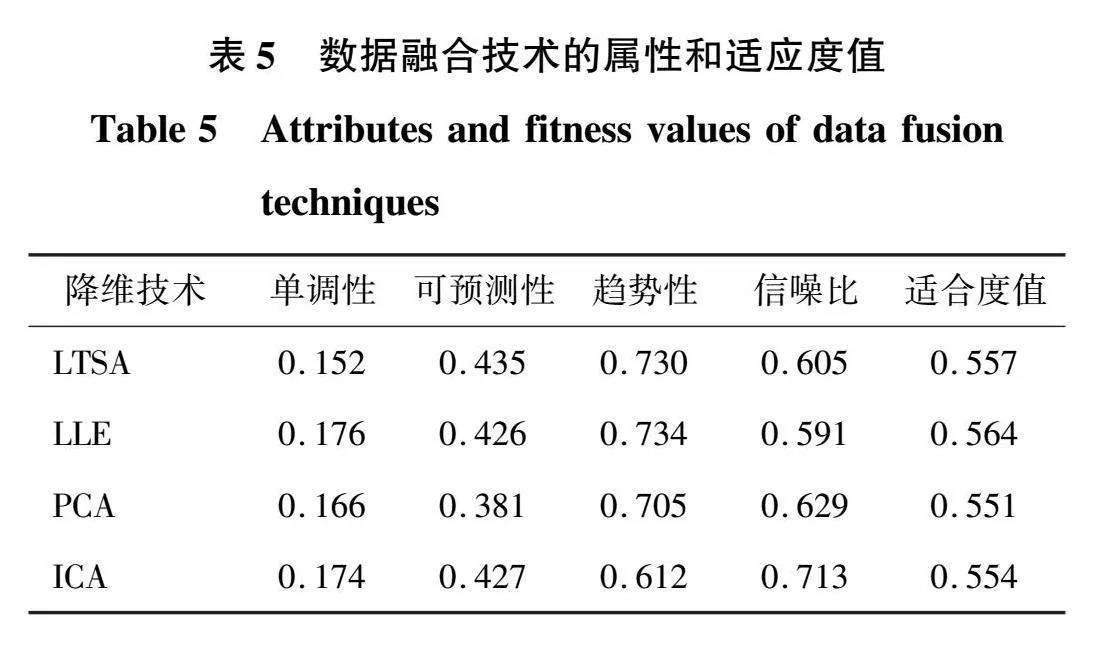
通过4个维度单调性、可预测性、趋势性、信噪比，进行加权和来确定适合度指标，如表5所示，这些参数的范围可以从0到1不等。0表示某一参数得分较低，表示该参数不适合进行剩余使用寿命（remaining useful life，RUL）预测;值1表示该参数得分最高，更适合于RUL预测，从而建立有效正确的轴承剩余使用寿命模型。

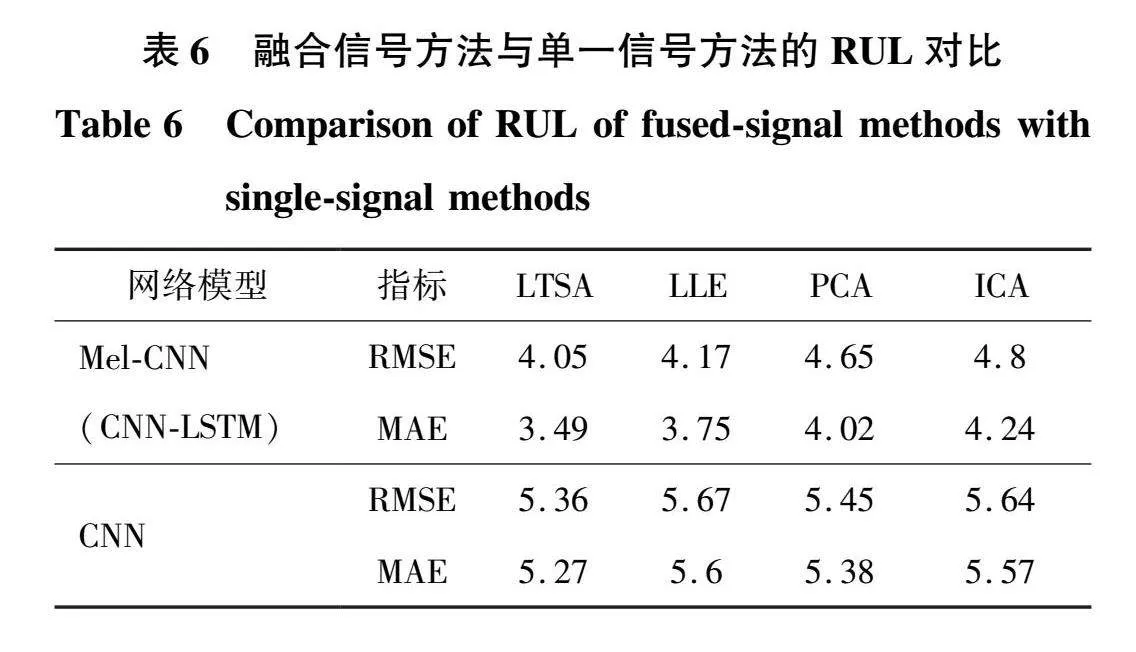
Mel-CNN融合电流模型预测了训练数据中每一步轴承的剩余使用寿命，对比4种降维技术 LTSA、LLE、PCA、ICA，通过计算均方根误差（root mean squared error，RMSE）和平均绝对误差（mean absolute error，MAE）2个指标来评估基于数据融合的LSTM方法的RUL性能，结果如表6所示。

由表6可知，Mel-CNN（CNN-LSTM）即长短期记忆卷积神经网络，对比于传统基于单一信号的CNN的RMSE，MAE的值都较低，则RUL预测的性能对比单信号取得了良好的效果。

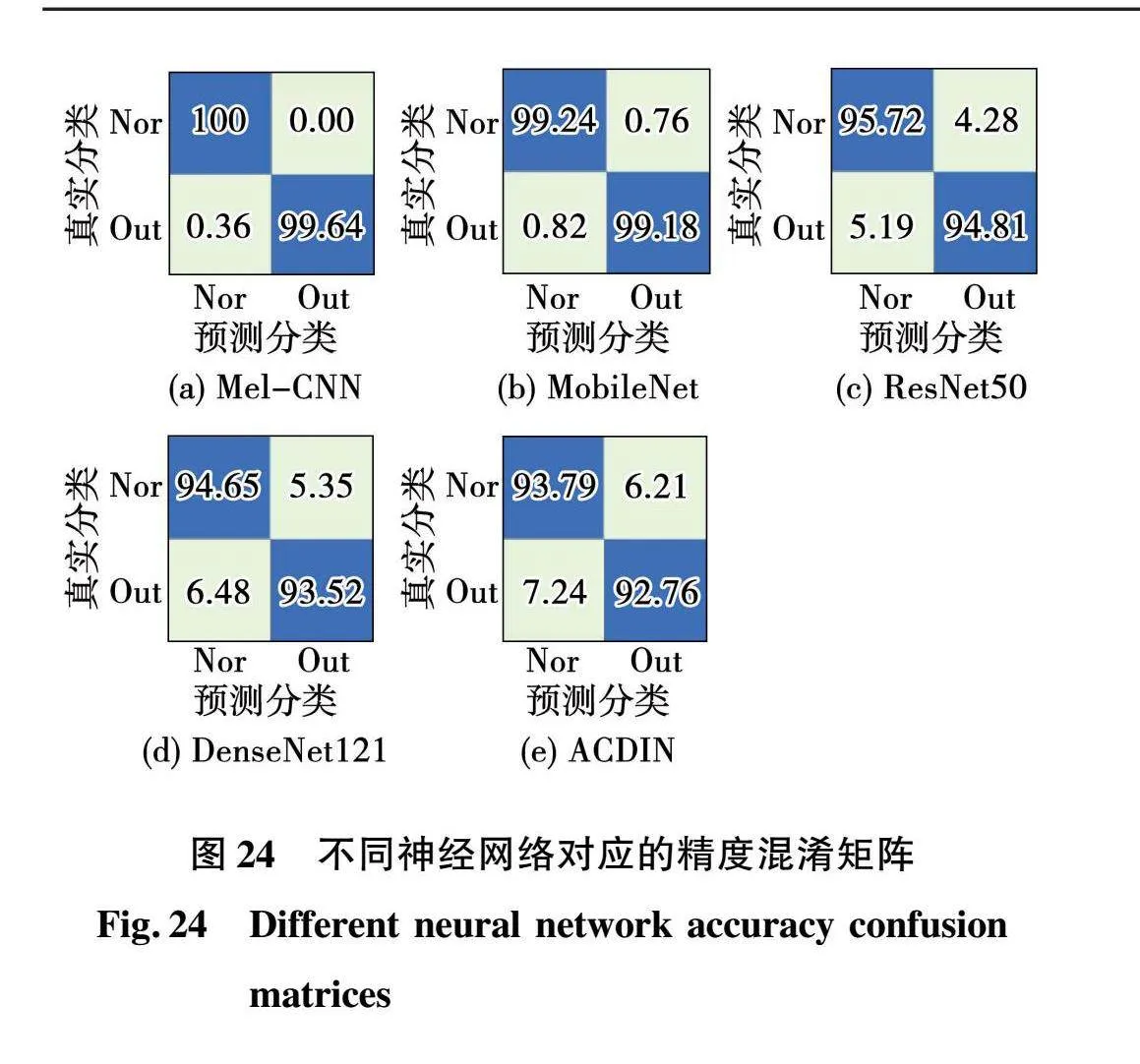
为了分析上述轴承故障诊断模型对外滚道缺陷轴承类型的识别效果，引入混淆矩阵来表示训练模型对测试集中故障样本的识别精度。所得结果如图24所示。

由图24可以看出，Mel-CNN模型和MobileNet模型对轴承类型的识别率最高，健康轴承或者外滚道缺陷故障轴承的识别准确率均达到99%以上。Mel-CNN模型对Nor类型的识别效果优于其他4种类型，准确率达到100%，MobileNet模型相对与Mel-CNN来说，准确率下降，误判概率增大。剩余3种模型的识别准确率相对较低，未达到准确辨别状态的要求。综合来说，Mel-CNN模型识别准确率最高，优于其余识别模型。

4 结 论

在不适合振动信号作为检测量的轴承外圈故障诊断的情况下，提出一种基于声信号的识别方法。基于Mel-CNN和电流频谱的电机轴承外圈故障声纹检测方法，并给定一定的负载变化，通过定子电流、变分模态分解分量以及声谱信号及其功率谱图来表征轴承外圈故障。结果表明：

1）Mel谱结合电流频谱特征能够准确地表征轴承外圈故障，优于传统的诊断方法。该方法有效区分了故障状态和健康状态。改进了神经网络在异步电动机轴承外圈故障检测中的缺陷。

2）经WOA优化后的VMD算法结合Mel-CNN模型的有效性和准确性，并具有迭代速度快、模型尺寸小的优点。

3）利用改进的小波阈值去噪模型，并结合定子电流作为异步电机轴承故障检测，获取实际正常工作情况和轴承故障时定子电流的解析结果，表征故障情况的相关特征量明显，分辨正确率较高。

但如何增强相关声信号对环境噪声的抗干扰性能以及如何降低转子出现偏心故障时，故障判断出现误判的情况，本文仍需要做深一步研究，这将成为下一步的思考方向。

参 考 文 献：

［1］ 宋向金， 赵文祥. 交流电机信号特征分析的滚动轴承外故障诊断方法综述[J].中国电机工程学报， 2022， 42（4）：1582.

SONG Xiangjin， ZHAO Wenxiang. A review of rolling bearing fault diagnosis approaches using AC motor signature analysis[J]. Proceedings of the CSEE， 2022， 42（4）： 1582.

［2］ 许伯强， 谢子峰， 陈思远， 等. 异步电动机滚动轴承外滚道故障诊断新方法[J].电机与控制学报， 2022， 26（4）： 1.

XU Boqiang， XIE Zifeng， CHEN Siyuan， et al. Diagnosis method of rolling bearing outer raceway fault in induction motors [J]. Electric Machines and Control， 2022， 26（4）： 1.

［3］ 王照伟， 刘传帅， 赵文祥， 等. 多尺度多任务注意力卷积神经网络滚动轴承故障诊断方法[J].电机与控制学报， 2024， 28（7）： 65.

WANG Zhaowei， LIU Chuanshuai， ZHAO Wenxiang， et al. Rolling bearing fault diagnosis with multi-scale multi-task attention convolutional neural network[J]. Electric Machines and Control， 2024， 28（7）： 65.

［4］ 李俊卿， 胡晓东， 耿继亚， 等. 基于DMD和改进胶囊网络的变工况轴承故障诊断方法[J].电机与控制学报， 2023， 27（11）： 48.

LI Junqing， HU Xiaodong， GENG Jiya， et al. Fault diagnosis method of variable working condition bearing based on DMD and improved capsule network[J]. Electric Machines and Control， 2023， 27（11）： 48.

［5］ JALAYER M， ORSENIGO C， VERCELLIS C. Fault detection and diagnosis for rotating machinery： A model based on convolutional LSTM and continuous wavelet transforms[J]. Computers in Industry， 2021， 31（6）： 1033.

［6］ WANG Xin， MAO Dongxing， LI Xiaodong. Bearing fault diagnosis based on vibro acoustic data usion and 1D-CNN network[J]. Measurement， 2021， 173（6）： 1085.

［7］ HOU Dongming， QI Hongyuan， LUO Honglin， et al. Comparative study on the use of acoustic emission and vibration analyses for the bearing fault diagnosis of high-speed trains[J]. Structural Health Monitoring， 2022， 21（4）： 1518.

［8］ 张重远， 罗世豪， 岳浩天，等. 基于Mel时频谱卷积神经网络的变压器铁芯声纹模式识别方法[J].高电压技术， 2020， 46（2）： 413.

ZHANG Chongyuan， LUO Shihao， YUE Haotian， et al. Pattern recognition of acoustic signals of transformer core based on Mel spectrum and CNN[J]. High Voltage Engineering， 2020， 46（2）： 413.

［9］ GLOWACZ A， GLOWACZ W， GLOWACZ Z， et al. Early fault diagnosis of bearing and stator faults of the single phase induction motor using acoustic signals[J]. Measurement， 2017， 113（15）： 1321.

［10］ 刘云鹏， 王博闻， 岳浩天， 等. 基于50Hz倍频倒谱系数与门控循环单元的变压器偏磁声纹识别[J].中国电机工程学报， 2020，40（14）： 4681.

LIU Yunpeng， WANG Bowen， YUE Haotian， et al. Identification of transformer bias voiceprint based on 50Hz frequency multiplication cepstrum coefficients and gated recurrent unit[J]. Proceedings of the CSEE， 2020， 40（14）： 4681.

［11］ WANG Chen， WANG Min， YANG Bin， et al. A novel methodology for fault size estimation of ball bearings using stator current signal[J]. Measurement， 2021， 171（6）： 1723.

［12］ 袁媛， 方红彬， 殷忠敏. 基于多数据融合的电机故障诊断方法研究[J].电气传动， 2021， 51（9）： 75.

YUAN Yuan， FANG Hongbin， YIN Zhongmin. Research on motor fault diagnosis method based on multi data fusion [J]. Electric Drive， 2021， 51（9）： 75.

［13］ ELSAMANTY M， IBRAHIM A， SALMAN W A. Principal component analysis approach for detecting faults in rotary machines based on vibrational and electrical fused data[J]. Mechanical Systems and Signal Processing， 2023， 37（12）： 1159.

［14］ 陈康， 安康， 王骁贤， 等. 基于振动和电流信号深度融合的电动机转速估计及轴承外圈故障诊断[J].轴承， 2023（2）： 54.

CHEN Kang， AN Kang， WANG Xiaoxian， et al. Estimation of motor speed and fault diagnosis of bearings based on deep fusion of vibration and current signals[J]. Bearing， 2023（2）： 54.

［15］ 杜文辽， 牛新闯， 王宏超， 等. 基于多因素干涉的滚动轴承故障动力学建模[J].煤矿机械，2024，45（7）：167.

DU Wenliao， NIU Xinchuang， WANG Hongchao， et al. Dynamic modelling of rolling bearing fault based on multi-factor interference[J]. Coal Mining Machinery， 2024， 45（7）： 167.

［16］ 张哲， 刘智丰， 肖仲喆， 等. 基于声信号的轴承故障检测算法研究与实现[J].电子器件， 2024， 47（3）： 656.

ZHANG Zhe， LIU Zhifeng， XIAO Zhongzhe， et al. Research and implementation of bearing fault detection algorithm based on acoustic signal[J]. Chinese Journal of Electron Devices， 2024， 47（3）： 656.

［17］ TOLIYAT H A， AREFEEN M S， PARLOS A G， et al. A method for dynamic simulation of air-gap eccentricity in induction machines[J]. IEEE Transactions on Industry Applications， 1996， 32（4）： 910.

［18］ CUI Lingli， LI Beibei， MA Jianfeng， et al.Quantitative trend fault diagnosis of a rolling bearing based on Sparsogram and Lempel Ziv[J]. Measurement， 2018， 128（11）： 410.

［19］ 邢挺， 范增盛， 马君梁， 等. 基于小波变换改进阈值函数的故障行波去噪方法[J].电工技术，2023（17）：37.

XING Ting， FAN Zengsheng， MA Junliang， et al. Denoising method of fault traveling wave based on wavelet transform improved threshold function[J]. Electric Engineering， 2023（17）： 37.

［20］ 刘明昊， 陆金桂， 张佳坤， 等. 基于VMD能量熵值的齿轮箱滚动轴承故障诊断[J].煤矿机械， 2023， 44（10）： 173.

LIU Minghao， LU Jingui， ZHANG Jiakun， et al. Fault diagnosis of gearbox rolling bearing based on VMD energy entropy[J]. Coal Mining Machinery， 2023， 44（10）： 173.

［21］ FENG Guorui， WEI huiru， QI Tingye， et al. A transient electromagnetic signal denoising method based on an improved variational mode decomposition algorithm [J]. Measurement， 2021， 173（11）： 1612.

［22］ JIN Shuaipu， WANG Xiufeng， DU Leilei， et al. Evaluation and modeling of automotive transmission whine noise quality based on MFCC and CNN[J]. Applied Acoustics， 2020， 121（7）： 1518.

［23］ LIN Zhaodong， DI Changan， CHEN Xiong. Bionic optimization of MFCC features based on speaker fast recognition[J]. Applied Acoustics， 2021， 173（5）： 1682.

［24］ 王勇， 宋玉宝， 魏春华， 等. 基于Mel谱特征提取的直升机声信号识别[J].计算机仿真， 2022， 39（5）： 66.

WANG Yong， SONG Yubao， WEI Chunhua， et al. Recognition of helicopter acoustic signal recognition based on Mel spectrum feature extraction[J]. Computer Simulation， 2022， 39（5）： 66.

［25］ 唐君， 张连海， 李嘉欣. 基于CBHG的Mel谱精细结构重建[J].信息工程大学学报， 2022， 23（2）： 135.

TANG Jun， ZHANG Lianhai， LI Jiaxin. Fine structure reconstruction of Mel spectrum based on CBHG[J]. Journal of Information Engineering University， 2022， 23（2）： 135.

［26］ WANG Xingqing， LI Yanfeng， FEI Jianchao， et al. Bearing fault diagnosis method based on Hilbert envelope spectrum and deep belief network[J]. Journal of Vibroengineering， 2015， 17（3）： 1295.

［27］ GUO Menghao， XU Tianhua， HU Shimin， et al. Attention mechanisms in computer vision： A survey[J]. Computational Visual Media， 2022， 8（3）： 331.

（编辑：刘琳琳）