基于超分辨率广义互相关算法的局部放电超声定位技术

摘 要：目前基于到达时间差法的局部放电超声定位方法被广泛应用于电力设备的局部放电检测，而现有方法存在有限采样率下时间差估计算法时间分辨率有限的问题，从而导致定位结果准确性不高。为突破采样率的限制，提出一种超分辨率广义互相关算法。该算法首先对信号进行阈值降噪预处理，以减小噪声对时间差估计精度的影响；在广义互相关框架下在频域内进行乘方操作，增加时间分辨率；设计迭代估计方法，搜索到精确的时间差估计结果；对每次迭代后的视在图像进行峭度分析，判断迭代终止次数。通过仿真分析验证了所提方法的可行性、不同加权函数下的性能和抗噪能力。最后通过实验验证，相比于传统的广义互相关算法，所提方法的定位精度在各采样率下均有较大提高。

关键词：局部放电；超声定位；到达时间差；超分辨率；广义互相关

DOI：10.15938/j.emc.2024.11.001

中图分类号：TM855

文献标志码：A

文章编号：1007-449X（2024）11-0001-11

Partial discharge ultrasound localization based on super-resolution generalized cross-correlation estimation algorithm

GUAN Yu， DONG Ming， WANG Hao， LIU Yinkang， WANG Bin， ZHANG Chongxing， REN Ming

（State Key Laboratory of Electrical Insulation and Power Equipment， Xi’an Jiaotong University， Xi’an 710049， China）

Abstract：The ultrasonic localization method for partial discharge based on the arrival time difference method is widely used in the detection of partial discharge in power equipment. However， existing methods suffer from limited time resolution of time difference estimation algorithms under low sampling rates， which leads to divergence of localization algorithms. To overcome the constraints imposed by sampling rates， a super-resolution generalized cross-correlation algorithm was introduced. In the algorithm， the signals were preprocessed to reduce the impact of noise on time difference estimation accuracy， exponentiation was performed in the frequency domain within the framework of generalized cross-correlation to enhance time resolution， an iterative estimation method was employed to search for precise time difference estimates， and kurtosis analysis was conducted on the apparent images after each iteration to determine the termination criteria. Through simulation analysis， the feasibility， performance under different weighting functions， and noise robustness of this method were verified. Finally， through experimental verification， compared to traditional generalized cross-correlation algorithms， the positioning accuracy of our method has been significantly improved at various sampling rates.

Keywords：partial discharge; ultrasound localization; time difference of arrival; super resolution; generalized cross correlation

0 引 言

局部放电（partial discharge，PD）是电介质绝缘材料局部区域因电场超过耐受而产生的放电现象，其会对材料绝缘性能产生影响，故局部放电既是导致绝缘击穿的重要因素，也是绝缘劣化的关键特征^[1]。目前，对电力设备开展局部放电现场检测一直是保障设备安全可靠运行的主要手段，尤其放电源精准定位对维修决策制定、实现精准维修更具实际意义。因此，探索更为直观、准确和快速的放电源定位方法对于电力设备早期故障预警、开展状态检修以及确保供电可靠性等方面至关重要^[2]。

局部放电超声定位方法根据其技术角度可分为：基于时差的到达时间法^[3-4]（time of arrival，TOA）和到达时间差法^[5]（time difference of arrival，TDOA）、基于角度的波达方向法^[6]（direction of arrival，DOA）、基于波形分析的波形分析法和信号强度法^[7]（received signal strength，RSS）等。其中TDOA算法可精确定位到局部放电源坐标，且具有较低硬件要求和计算复杂性，适用于广泛应用场景^[8]。

TDOA方法涉及时间差估计和空间定位两部分，其中时间差估计是定位准确的前提与基础。传统的固定式超声传感器在实际应用时受到多方面限制^[9]，如安装位置有限、维修困难等，而便携式传感阵列系统更具灵活、便携及低成本等诸多优点，更适用于复杂多变的现场应用需求。

对于厘米级阵元间距的超声阵列，其时间差估计的精度需达到纳秒级，而现场应用较多的广义互相关法^[10]（generalized cross correlation，GCC）和能量累积法^[11]等方法均未能有效解决这些限制对时延估计的需求与挑战。文献[2]提出基于小波图像卷积的时间差估计方法，该方法相比于传统的时间差估计方法具有更高的抑制噪声能力。但该方法计算复杂度大，难以满足电力设备实时监测的需求。文献[12]提出一种基于多样本能量相关搜索的时间差提取方法，该方法对多次放电信号的时间差取平均值，来获得更精确的时间差估计精度。但每次时间差的求取仍受采样率的限制，且局部放电具有随机性，该方法在实际中的应用具有一定困难。文献[1]提出一种新的线性频率调制混合信号时延估计方法，在低信噪比条件下在精度和最小均方误差方面表现更优，同时具备通过斜率比较实现时延匹配的能力，但精度受到采样点数量限制。上述方法没有解决定位受时间分辨率限制带来的系统误差，而时间差估计精度往往又受检测设备采样率、成本等诸多因素限制而难以提高^[14-15]，因此亟需一种新型时间差估计算法以突破设备采样率引入的系统误差影响。

本文在时间差估计领域提出的超分辨率含义为在有限采样率下能使时间差估计的精度突破采样时间间隔，即超采样时间间隔分辨率的一种时间差估计方法。已有学者通过直接在时域对信号进行插值来缩短采样时间间隔，以达到超分辨率时间差估计的效果^[16-17]，但其缺乏强理论支撑，且插值可能会影响两同源信号之间的相关性，影响时差估计效果。

为了解决有限采样率条件下时间差估计算法时间分辨率不足问题，基于超采样时间间隔思想，本文提出一种超分辨率时间差估计（super-resolution time difference estimation，SRGCC）算法，重点关注超分辨率时间差估计的性能，聚焦于开放空间中的无遮挡局部放电定位，可与其他方法相结合应用于更广泛的测距、定位等领域。首先，依托广义互相关理论，介绍了超声信号预处理、乘方操作、峭度分析等步骤，从原理上扩展了信号加权互功率谱函数的频谱，实现了时间差估计差值的降低，并通过迭代分析完善了时间差准确提取的相关理论。其次，提出超分辨率时间差估计算法的具体计算流程和步骤，结合理论仿真分析，验证了SRGCC算法的可行性及准确性，分析对比了不同加权函数下SRGCC收敛特性。最后，在实验室搭建了局部放电定位实验平台开展局部放电定位实验，将本文方法和粒子群算法相结合进行时间差估计与局部放电定位。结果表明，本文所提方法的定位精度相比传统方法在各采样率下均有较大提高。

1 TDOA超声定位数学模型

三维空间中，假设局部放电源位置坐标为T（x，y，z），采用麦克风阵列采集超声传感信号，其中麦克风的坐标依次为：S1（x1，y1，z1），S2（x2，y2，z2），…，Sn（xn，yn，zn）。ti表示超声信号从局部放电源传播至超声传感器Si所需的时间；tij=tj-ti表示信号传播至超声传感器Si与Sj之间的到达时间差，其中i=1，2，…，n-1，j=i+1，…，n；v表示超声信号在当前介质中的传播速度。

使用TDOA算法进行声源定位，各超声传感器与局部放电源的三维坐标之间满足距离关系，表达式为：

（x－x2）2+（y－y2）2+（z－z2）2－

（x－x1）2+（y－y1）2+（z－z1）2=vt21；

（x－x3）2+（y－y3）2+（z－z3）2－

（x－x1）2+（y－y1）2+（z－z1）2=vt31；

…

（x－xn）2+（y－yn）2+（z－zn）2－

（x－x1）2+（y－y1）2+（z－z1）2=vtn1。（1）

其中，可通过时延估计算法求得各超声传感器接收超声信号之间的时间差tij，进一步通过求解距离方程组来确定局部放电源的存在位置，即为各距离方程表示球面的交点。

求解三维空间中的定位方程至少需要4个超声传感器组成阵列。当传感器数目超过4个时，相互之间的冗余信息将导致方程组个数超过未知量个数，此时方程组可通过粒子群算法等启发式优化算法求解。时间差估计的准确与否，对定位的精确度至关重要。

2 超分辨率广义互相关时间差估计算法

广义互相关算法能够准确地估计两信号之间的时间差，但其受到信号采样率限制，导致时间差估计值是以采样时间间隔为差值的离散值，制约了时间差估计的精度。基于此，本文提出SRGCC算法，其基本思想为：对两信号加权运算后的互功率谱函数乘方操作，扩展信号频谱，从而减小时间差估计的差值，再采用迭代估计实现时间差准确提取，以有效提高时间差估计的分辨率。

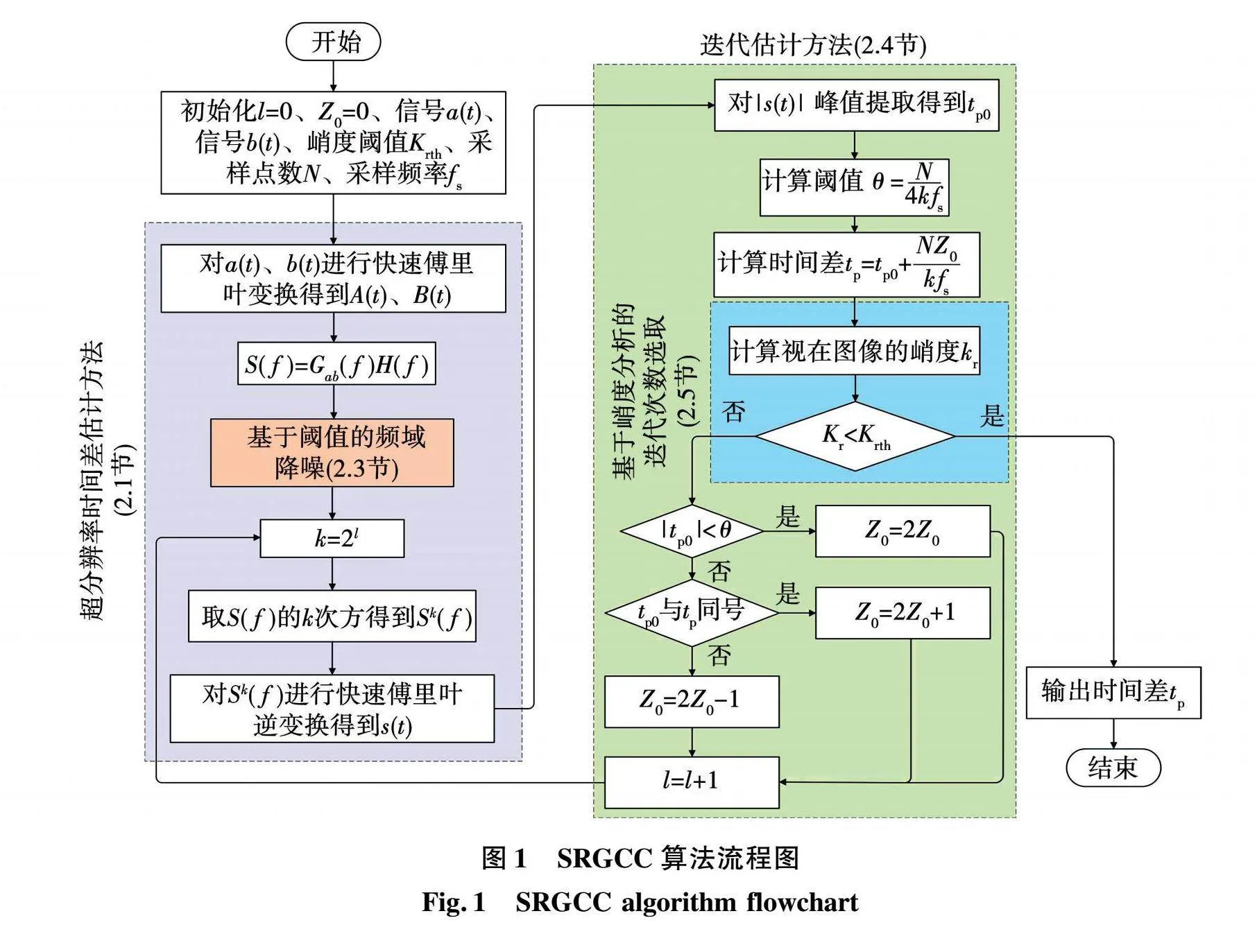
SRGCC在频域的乘方操作等效为时域的互相关操作，实际情况中多次互相关会导致信号受噪声的影响增强，从而加大时间差估计的误差。因此信号的畸变和噪声会影响SRGCC算法的估计性能，也导致了算法的迭代次数不能无限大。针对此，本文还提出信号预处理方法和基于峭度分析的迭代次数选取方法。为展示本文算法各部分的关系，本文算法的流程图如图1所示。

2.1 超分辨率时间差估计方法

基于TDOA的定位方法中，数字麦克风采集到的两通道局部放电超声信号表达式为：

a（t）=A1s0（t－t1）+n1（t）；（2）

b（t）=A2s0（t－t2）+n2（t）。（3）

式中：A1和A2表示信号幅值；s0（t）表示原始局部放电超声信号；n1（t）和n2（t）表示噪声且n1（t）、n2（t）和s0（t）互不相关；t为离散时间变量，表达式为

t=nfs，n=0，1，…，N－1。（4）

式中：N为采样点数；fs为采样频率。

将离散时间信号a（t）和b（t）经傅里叶变换到频域，得到频域离散序列，其表达式为：

A（f）=A1S0（f）e^－j2πt1f+N1（f）；（5）

B（f）=A2S0（f）e^－j2πt2f+N2（f）。（6）

式中f=0，1Nfs，2Nfs，…，N－1Nfs。

将A（f）与B（f）共轭相乘，且由于n1（t）、n2（t）和x1（t）互不相关，可得两者的互功率谱Gab（f）为

Gab（f）=A（f）B（f）=A1A2|S20（f）|e^{－j2π（t1－t2）f}+

A1S0（f）e^－j2πt1fN2（f）+

A2S0（f）e^－j2πt2fN1（f）+N1（f）N2（f）=

A1A2|S20（f）|e^{－j2π（t1－t2）f}=

A1A2|S20（f）|e^－j2πt0f。（7）

式中t0为a（t）和b（t）之间的理论时间差。

对Gab（f）进行加权函数运算，定义加权函数为H（f），在信号与噪声各互不相关且采样时长无限长的理想情况下有

S（f）=Gab（f）H（f）=e^－j2πt0f。（8）

该表达式为冲激函数的频域形式，但由于数据离散化的原因，式（8）经离散傅里叶逆变换到时域会出现冲激函数特征的离散化表达，可通过对冲激函数峰值所对应时间直接提取时间差，其分辨率为1/fs。而依据奈奎斯特采样定律，当采样率超过被采信号最大频率的2倍时即可无失真的恢复原有信号，因此若采样时间无限长，当信号不存在频谱泄漏时，因时域采样分辨率导致的时间差估计误差可无限缩小。这为SRGCC算法的提出提供了理论支撑。

对式（8）进行k次方操作，对频谱进行扩展，从而实现频率调整，达到了后面超分辨率时间差估计的效果，则有

Sk（f）=e^－j2πkt0f。（9）

进一步对式（9）中的t0以t′0近似估计，有

t′0=n0fs。（10）

式中n0与k相乘后的值为[-kN/2， kN/2]内的整数，使得t′0最接近t0。

对S^k（f）进行离散傅里叶逆变换，可得

s（n）=1N∑N－1Nfsf=0e^－j2πkt0fe^j2πtf=1N∑N－1Nfsf=0e^{j2π（t－kt0）f}，

f=0，1Nfs，2Nfs，…，N－1Nfs。（11）

将式（11）通过等比数列求和公式求和，可得

s（t）=1N1－e^{j2πfs（t－kt0）}1－e^{j2πfsN（t－kt0）}。（12）

对式（12）取绝对值，以保证实际s（n）的最大峰值为正，可得

|s（t）|=1N1－e^{j2πfs（t－kt0）}1－e^{j2πfsN（t－kt0）}。（13）

在式（13）中，用t′0近似t0并将式（4）和式（10）代入，可得

|s（n）|=1N1－e^{j2π（n－kn0）}1－e^{j2πN（n－kn0）}。（14）

式（14）中，当n=kn0+NZ时，|x（n）|会出现峰值，记此时的n为n1，其中Z表示整数集。又由式（10）可得

t′0=1kfsn1+NkfsZ。（15）

式（15）说明了SRGCC算法得到的时间差提取函数的函数图像性质，该性质将在2.2节进行讨论。

2.2 SRGCC算法实现超分辨率时间差估计能力的讨论

本节就超分辨率时间差估计的具体含义和2.1节中的SRGCC推导过程中的关键步骤进行阐述和分析。

超分辨率时间差估计示意图如图2所示，采样得到的信号为以采样时间间隔为差值的离散时间信号，通过传统时间差估计方法得到的时间差估计值只能逼近时间轴上的离散时间点，由此带来了时间差估计的系统误差。而本文提出的超分辨率时间差估计为突破采样带来的时间分辨率限制，使时间差估计值逼近时间差真值。

为起到超分辨率的效果，关键在于式（9）中的k次方操作，其从冲激函数的频域性质出发，进行了频域调整，从而起到了超分辨率的效果。

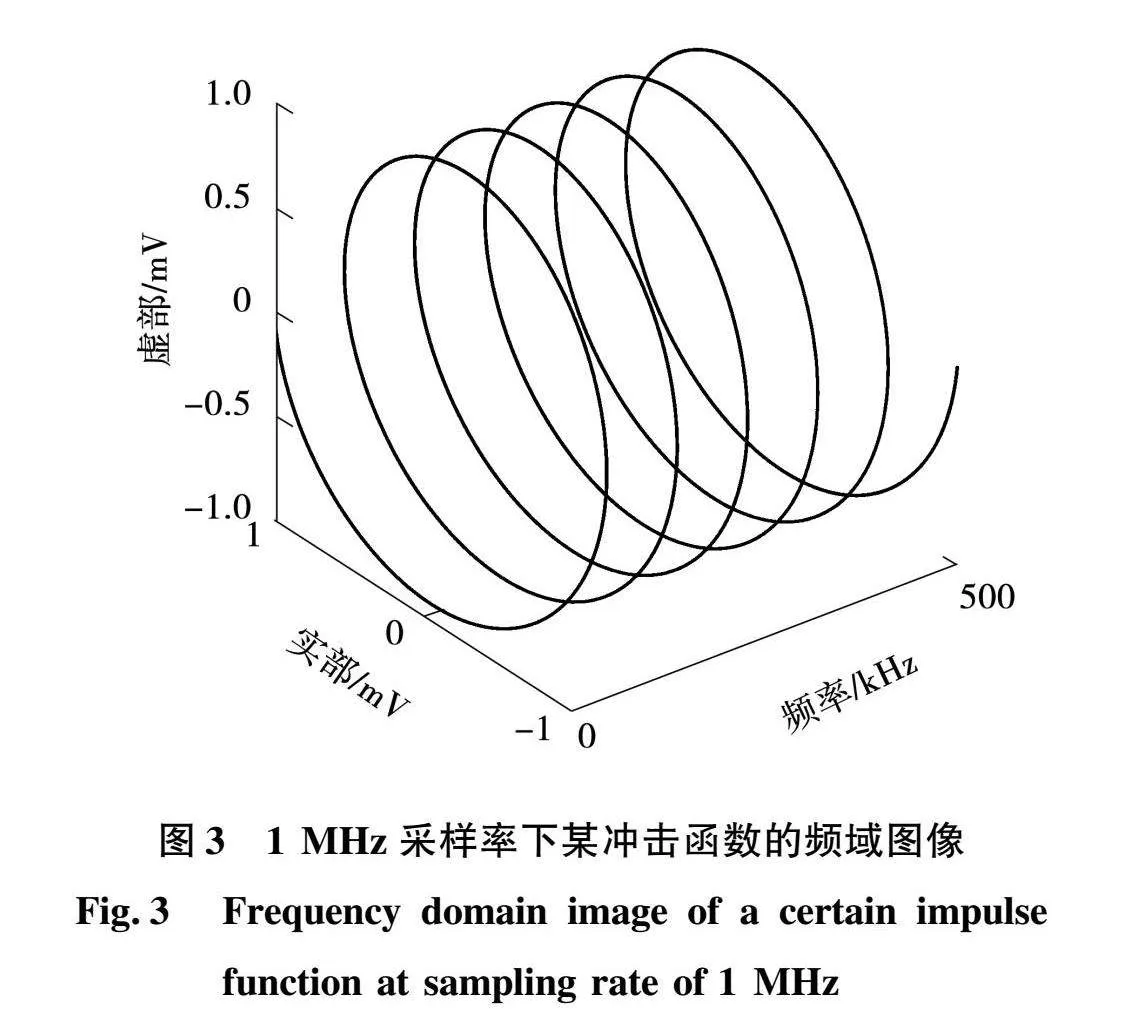
对于1 MHz采样得到的一对同源信号，可通过广义互相关算法得到式（8）所示的冲激函数频域表达式，其函数图像如图3所示。若将该表达式进行2次方操作，可得到频域调整后的函数图像如图4所示。图3所示的函数图像和图4所示的函数图像形状一致，可以反应同样的时间差，但图4中反应采样率的最高频域提升到了图3中最高频率的2倍，即图4时间差估计的精度可提升到2倍采样率的效果，通过算法起到了采样率的提升。同理，式（9）中的k次方操作可以使时间差估计的精度超分辨率地提升到k倍采样率的效果。

由于时域采样点为N，|s（n）|中n的取值范围为[-N/2，N/2]。虽然式（9）中的k次方操作可以提升采样率，但由于采样点数不变，所以经以上方法计算得到的时域函数图像反映的时域范围会缩小k倍，由[-N/2fs，N/2fs]缩小到[-N/2kfs，N/2kfs]，记该图像为视在图像。同样由式（15）可知，该式的第一项表示真实的时间差估计值tp，第二项表示该峰值会以N/kfs为倍数在时域内重复出现，当|tp|大于|N/2kfs|时，视在图像内峰值提取的结果为本文称作tp0，表示真实时间差估计值的峰值tp会在视在图像外出现，无法直接得出，如图5所示。所以需要后续的迭代方法来求解真实的时间差。

2.3 信号预处理方法：基于阈值的频域降噪

局部放电定位技术更注重同源信号不同信道之间有效信号的相关性，同时由于放电信号具有窄带信号特性，且在频域幅度谱较大，而局部放电信号的干扰信号往往在频域幅度谱较小且分布比较平均。为了最有效地保留两信号中有效信号之间的相关性，本文将文献[18]中的频域阈值处理方法应用于SRGCC算法中信号去噪环节，具体操作如下：

Step1：求S（f）的幅度谱函数|S（f）|；

Step2：根据|S（f）|估计反应噪声频域最大值特征的幅度AF；

Step3：计算阈值T=λAF；

Step4：将S（f）中幅度谱小于T的值置零。

其中λ应选大于1的值，推荐选取的范围为 5～6。

2.4 超分辨率时间差的迭代估计方法

由图5可知，随着式（9）中k次方次数的增加，表示时间差的峰值可能在视在图像外出现，视在图像里峰值所在时间与理论时间差之间为N/（kfs）的倍数。为获得准确时间差，本文提出迭代求解方法。

由式（15）可得，准确的时间差估计值为

tp=tp0+NZ0kfs。（16）

式中Z0为一整数。

为求解到唯一正确的Z0，进行如下规定：两通道同源信号的采样时间应大于2倍该两信号的时间差，以保证在视在图像内会出现时间差提取的峰值；式（9）的乘方操作为以2为底数的指数递增。每次求解得到的时间差与阈值θ进行比较，阈值θ的表达式为

θ=N4kfs。（17）

迭代开始之前，令Z0为0。在第l次迭代时，进行以下操作：

Step1：对|s（t）|^l峰值提取得到t^lp0；

Step2：将k=2^l、t^lp0和Z^l0代入式（16）得t^lp；

Step3：计算θ^l，将t^lp0与θ^l进行比较：

若|t^lp0|lt;θ^l，则Z^l+10=2Z^l+10；

若|t^lp0|gt;θ^l且t^lp0与t^lp异号，则Z^l+10=2Z^l0－1；

若|t^lp0|gt;θ^l且t^lp0与t^lp同号，则Z^l+10=2Z^l0+1；

由于计算机中的离散傅里叶变换和离散傅里叶逆变换是通过快速傅里叶变换和快速傅里叶逆变换实现的，仅仅增加了乘方和迭代操作，所以本文方法的运算速度较快。

2.5 基于峭度分析的迭代次数选取方法

SRGCC算法中的乘方操作会指数级地增加信号的畸变和噪音对时间差估计的影响，为了寻求在合适的条件结束迭代，本文提出基于峭度分析的迭代次数选取方法。峭度计算方法为

Kr=1N∑Nk=1（sk－s-）41N∑Nk=1（sk－s-）22。（18）

式中：Kr为信号的峭度；sk为信号在第k个采样点上的强度，k=1，2，…，N；s-为信号强度的均值。

峭度可以反应观测值的分散程度，当分散程度小时，峭度增大，信号的峰值比较明显。本文对每次迭代后的视在图像进行峭度分析，随着迭代次数的增加，s（t）的峭度会不断减小。可根据实际信号的噪声和畸变情况选取峭度阈值，信号的噪声和畸变越大，应选择更大的峭度阈值。当峭度小于该阈值时停止迭代。

3 时间差估计仿真及分析

由于广义互相关框架下有不同的加权函数，不同的加权函数会影响算法的时间差估计结果，本文在无噪和含噪情况下，分别对使用不同加权函数的SRGCC算法进行了讨论。

双指数脉冲信号具有快速上升和缓慢衰减的特征，和实际局部放电超声信号的波形具有相似性，所以本文采用双指数振荡脉冲信号模拟局部放电波形，表达式为

s（t）=Ae^{－1.3（t－t0）τ}－e^{－2.2（t－t0）τ}sin（2πf0（t－t0））。（19）

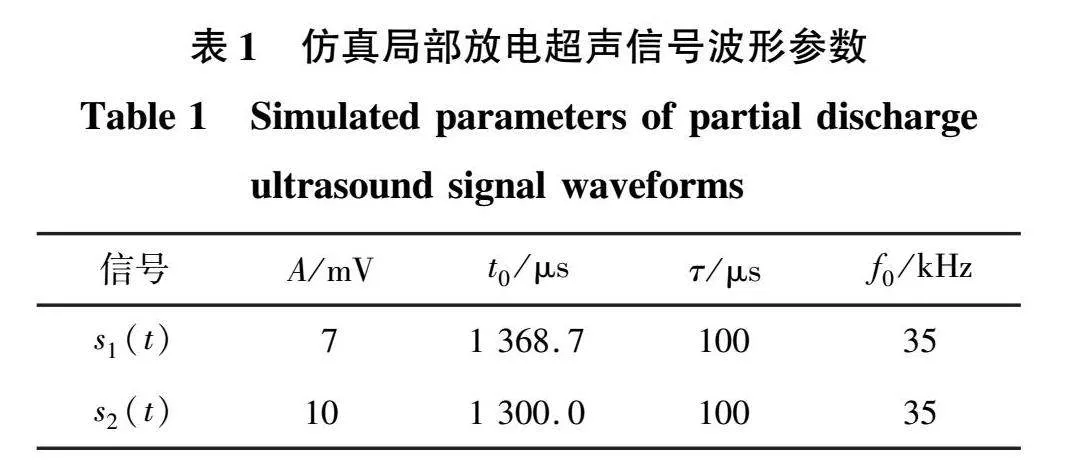
式中：A表示信号振幅，mV；f0表示声源振荡的基准频率，kHz；t0表示信号起始时间，μs；τ表示信号的衰减系数，μs。仿真产生的两个局部放电超声信号波形参数如表1所示，信号的采样率为500 kHz，采样时间为3 ms。

由表1可知，信号s1（t）和s2（t）的时间差为68.7 μs，要求采样时间间隔为0.1 μs才能准确地估计到时间差，而实际采样时间间隔为2 μs。如果采用更精确的超声传感器采集信号，需要硬件的性能提高20倍，即设备采样率达到10 MHz。

3.1 SRGCC的时间差估计迭代过程

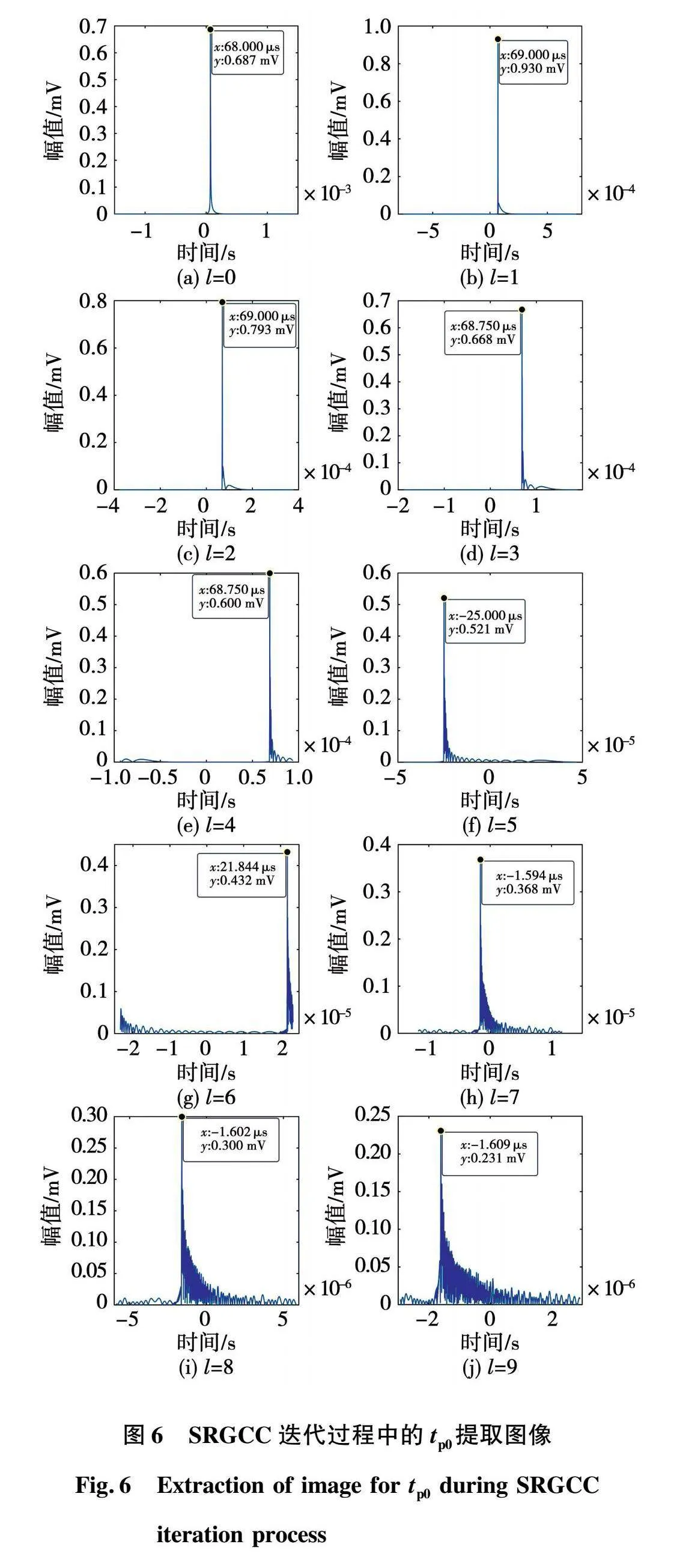
将信号s1（t）和s2（t）通过SRGCC算法进行迭代运算，峭度阈值选为10，最终得到的时间差收敛到68.703 μs，而通过传统的GCC算法得到的时间差为68 μs，证明了SRGCC可有效提高时间差估计的准确度。迭代前10次的tp0提取图像如图6所示，时间差在20次迭代中的收敛曲线如图7（c）所示。

由图6可得，随着迭代次数的增加，信号的主峰逐渐向右偏移，并且表示时间差的峰值在第6次迭代时超出了该图像的范围，此时图像内为一个次峰，提取该次峰对应的时间即为tp0，代入式（16）可计算出准确的时间差。

通过峭度分析可得，该算法在第10次完成收敛，时间差为68.703 μs，与理论时间差仍有0.003 μs的误差。分析其原因：1）本仿真模拟了实际局部放电超声信号，其频带理论上是无限宽，而采样过程中必然会造成高频信号丢失；2）采样时间窗大小有限，从而带来频谱泄漏。在满足奈奎斯特定律的条件下，当采样时间趋于无限大时，该算法为渐进无偏估计。

3.2 不同加权函数对SRGCC性能的影响

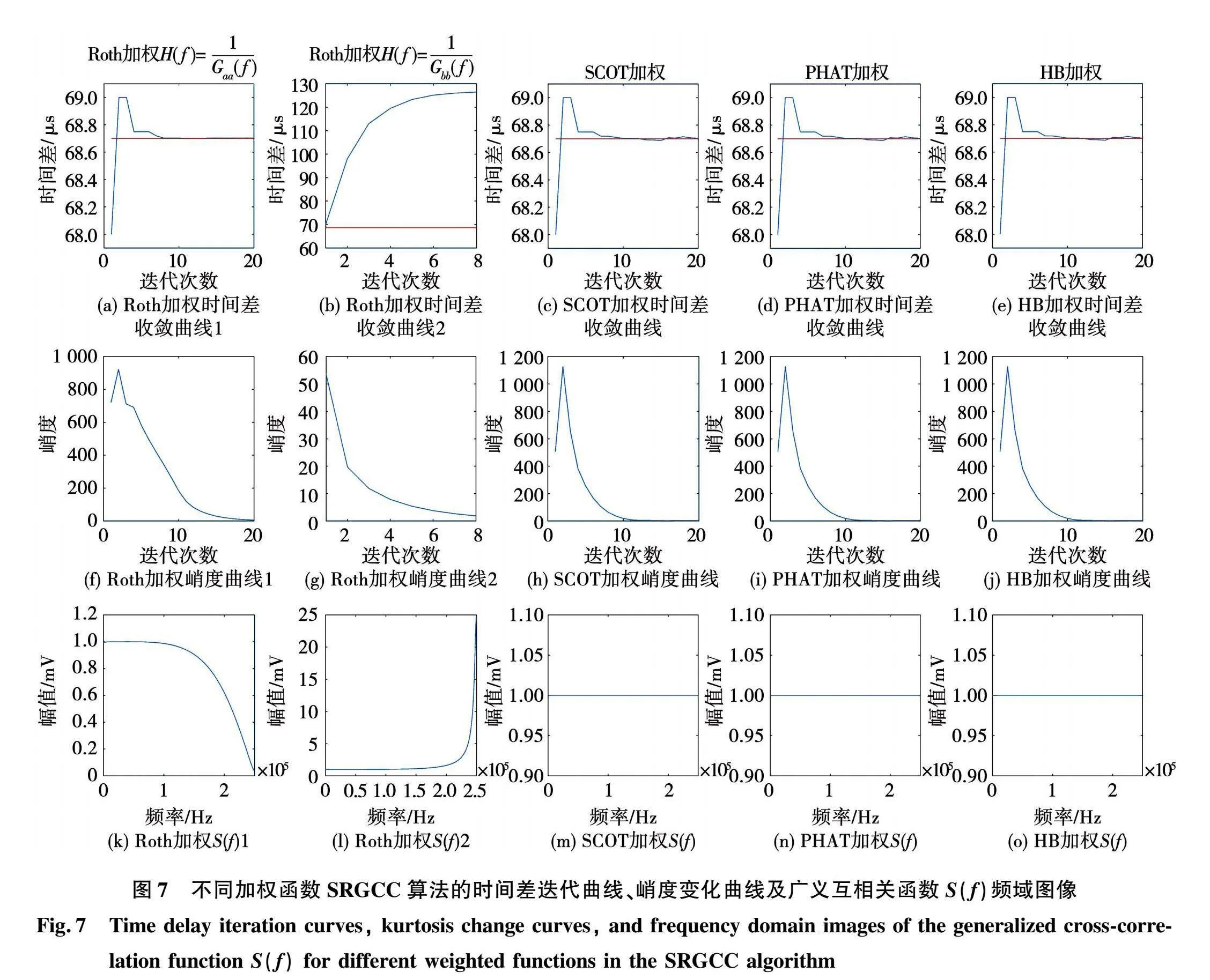
式（8）中广义互相关理论的经典加权函数如表2所示。将信号s1（t）和s2（t）通过采用该4种加权函数的SRGCC算法得到的时间差迭代曲线、峭度变化曲线及广义互相关函数S（f）频域图像如图7所示，图中的直线表示理论时间差。

由图7可得，因为Roth加权函数只采用Gaa（f）或Gbb（f）对互功率函数Gab（f）进行归一化，且麦克风以固定采样率采样，相当于对原信号的频谱加了矩形窗，必然会导致一定的频谱泄漏，使得Gaa（f）、Gbb（f）和Gab（f）三者的幅度谱不完全相同，其中的比例差异会通过加权运算反映出来，使得广义互相关函数S（f）的幅度谱在高频部分产生较大的变形，如图7（k）和图7（l）所示，从而不能保证为一条直线。这不仅仅使S（f）反映的冲激函数特征较弱，更使SRGCC算法后续的乘方操作中放大了频谱泄漏的影响，从而使数据溢出，如图7（b）所示。同样可以看出，图7（a）所示的曲线最终收敛于准确的时间差，而图7（b）所示的曲线最终发散，这与S（f）的高频部分是被削弱还是增强有关：当高频部分被削弱，算法可以收敛；当高频部分被增强，算法不能收敛。

SCOT加权、PHAT加权和HB加权这3种加权函数由于在运算过程中给两原始信号相同的权重，使S（f）的幅度谱为一条直线，从而更加突出了时间差的冲激函数特征，能够较小地受到频谱泄漏的影响。

该示例中的Roth加权SRGCC一个收敛一个发散，其中收敛的算法在第18次收敛，得到的时间差为68.704 μs。该示例中的SCOT加权、PHAT加权和HB加权SRGCC均在第10次收敛，得到的时间差为68.703 μs。说明SCOT加权、PHAT加权和HB加权在收敛速度和精确度上均优于Roth加权。

4 时间差估计与定位实验

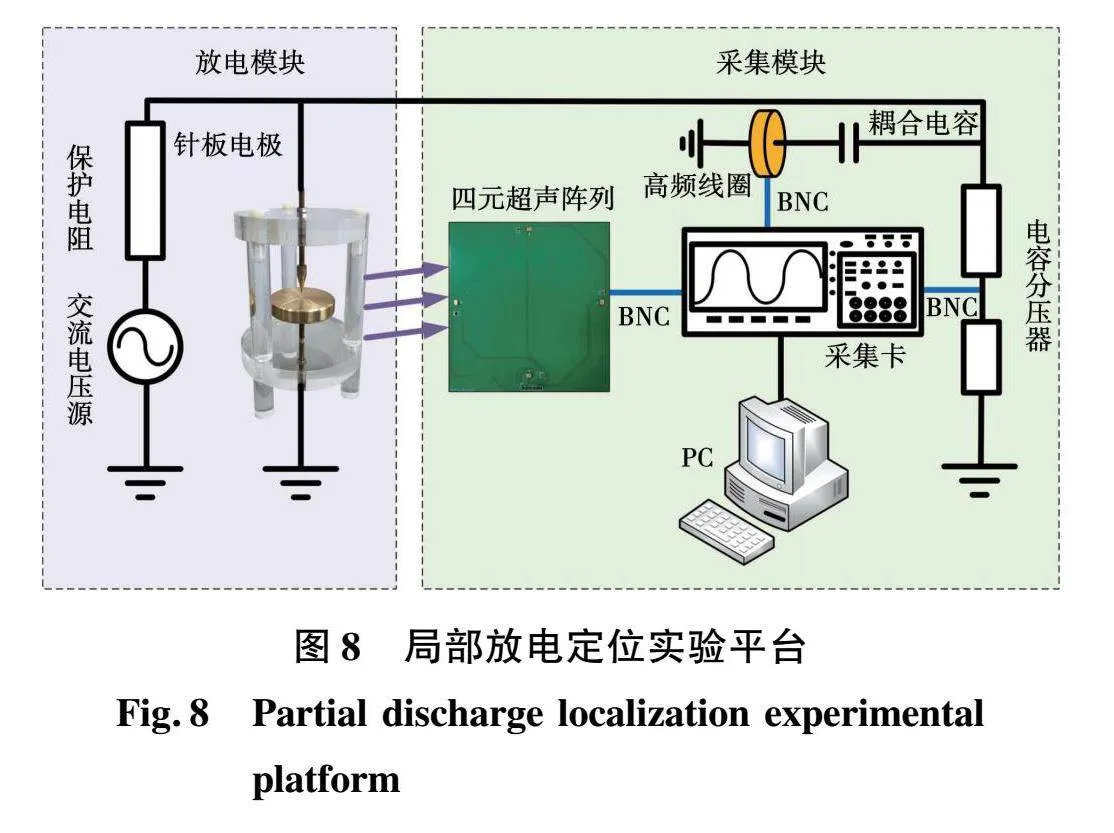
为验证本文方法能够有效在各采样率下提高定位精度，本文搭建了如图8所示的实验平台。实验变压器可提供0～100 kV的工频电压，2 000∶1的电容分压器测量施加在电极两端的电压，并通过高频线圈实现电极的局部放电信号检测。实验中放电电极结构采用针板电极，针板电极之间的距离为8 mm，表面及棱角处做光滑处理，放电介质为空气，实验环境温度为15 ℃。

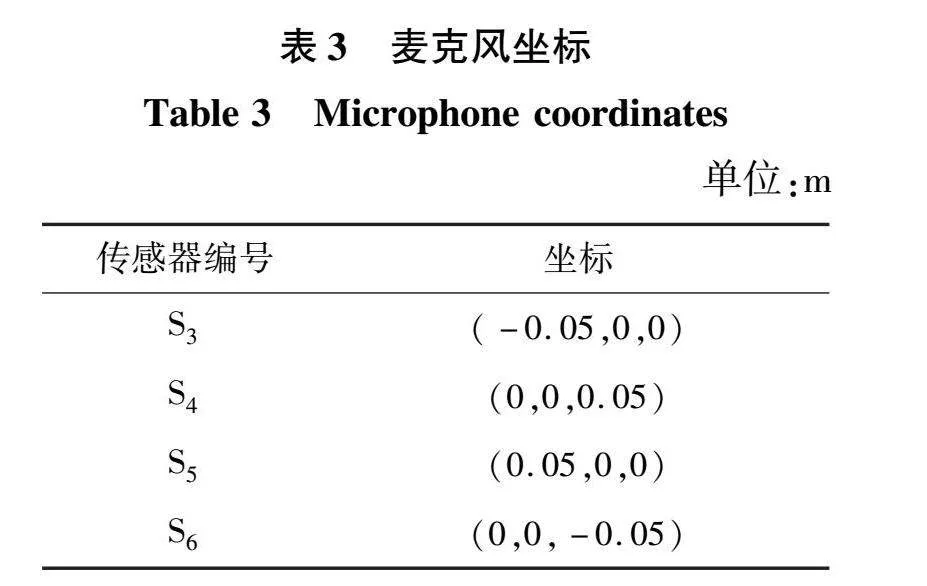
局部放电超声信号的采集使用四元麦克风阵列，并经BNC连接器通过PicoScope 5000系列数字采集卡将数据传递给个人电脑，该数字采集卡支持6通道信号同步采样，并且采样率可调，最大采样率支持1 GHz。表3为四元MEMS麦克风的坐标。

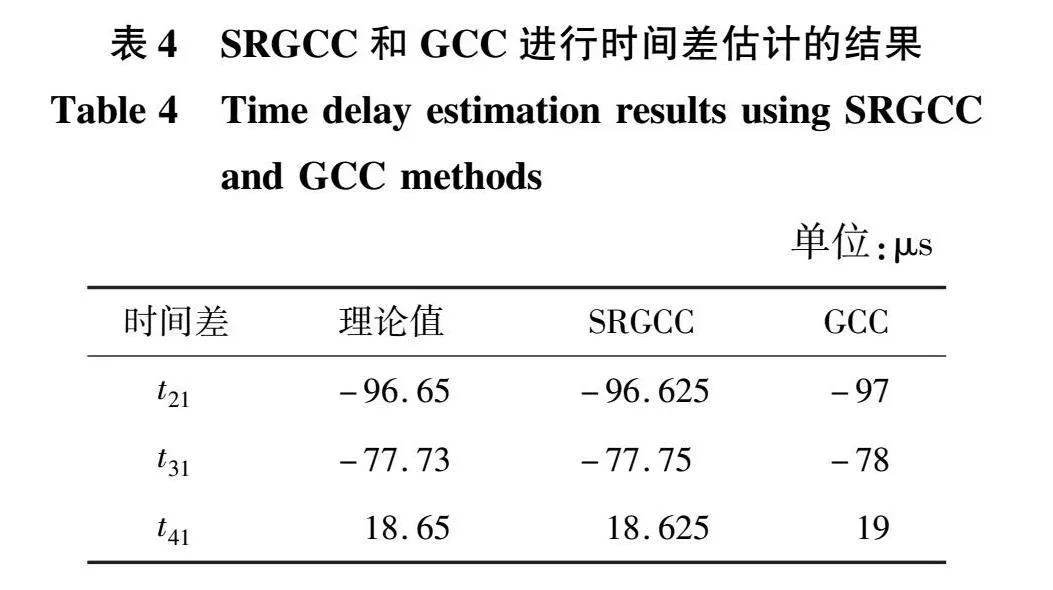
本次实验以传感器阵列的中心为原点，在阵列前方x轴范围-1～1 m、y轴范围0.5～2.5 m、z轴范围-1～1 m处进行多次局部放电试验，并分别使用1、10 MHz的采样频率进行采样。图9为四元麦克风利用1 MHz采样率采集到的坐标为（0.60，2.00，0.89）m的局部放电产生的超声信号通过本文算法得到的时间差估计迭代曲线和峭度迭代曲线。由于实际信号噪声比较复杂，本次实验峭度阈值选为100，通过本文算法和传统的广义互相关算法得到的时间差估计值如表4所示。表4和图9中，txy表示超声信号传播至传感器x和传感器y之间的时间差。

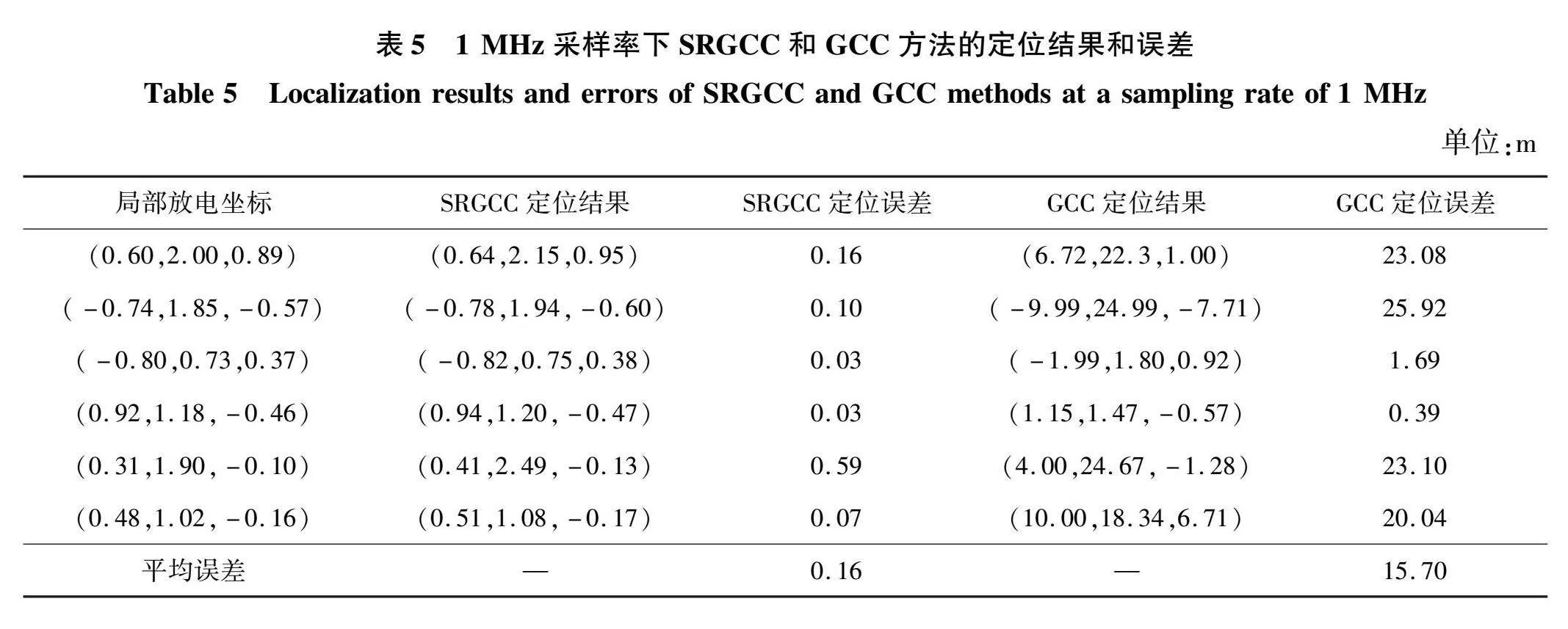
由表4可以看出，相比传统的广义互相关算法，本文方法更加逼近真实的时间差。求得局部放电超声信号到达不同传感器的时间差后，粒子群算法^[19]求解TDOA定位方程组得到局部放电坐标，其中粒子生成的范围为x轴范围-10～10 m、y轴范围0～25 m、z轴范围-10～10 m，计算结果如表5、表6所示，表中结果精确到小数点后两位。

由表5可得，第1、2、5、6次定位中基于GCC算法的定位由于时间分辨率不足，导致定位算法发散，完全无法起到定位的功能，第3、4次定位中基于GCC算法的定位可以起到定位的效果，但误差较大。而采用本文方法进行定位，在传统定位方法发散的情况下，仍然可以有效地定位到局部放电源，且定位精度也有效提高。

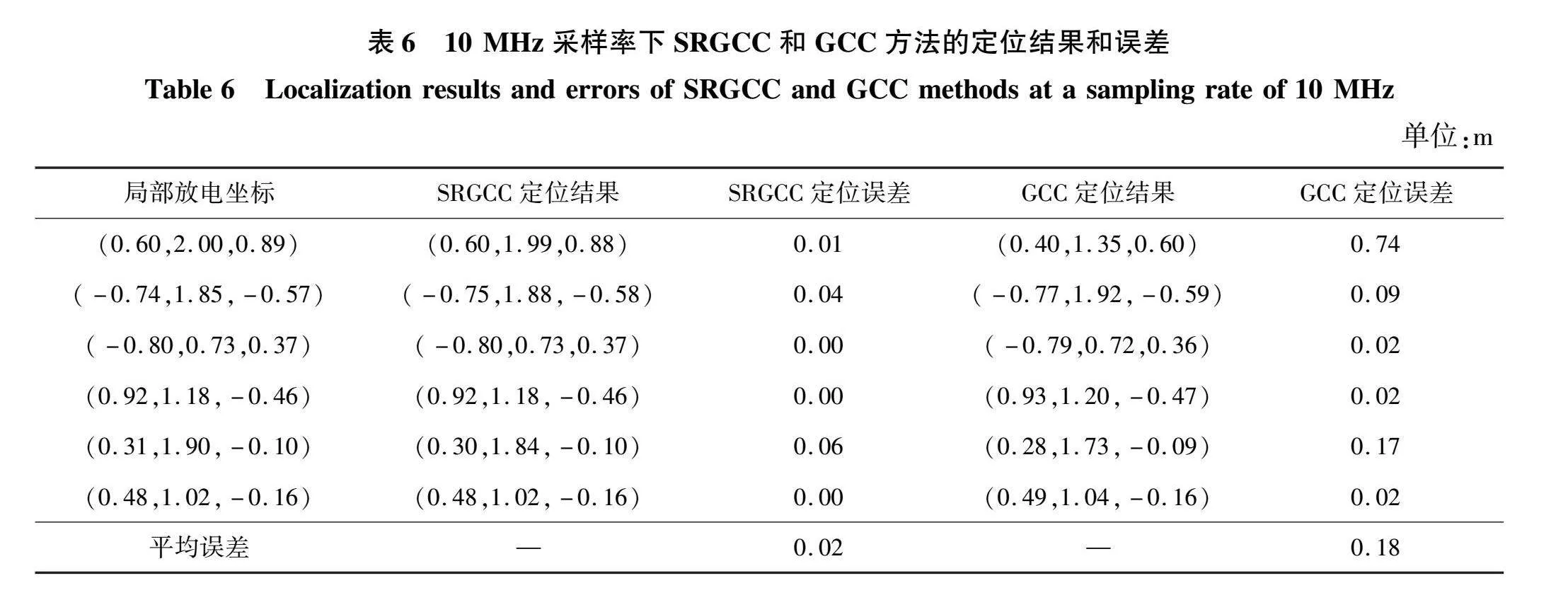
由表6可得，由于采样率的提高，基于GCC算法的定位精度也有所提高，但采用本文方法的定位可以起到更精确的定位效果。实验结果表明，本文方法在该阵元间距与1、10 MHz采样率条件下的定位平均误差位分别为0.16、0.02 m，比GCC算法的定位精度分别提高了98.98%、88.89%。

使用GCC进行时间差估计的定位方法可以反应传统的一系列非超分辨率时间差估计方法的定位结果，定位误差为系统误差，该误差不可通过分辨率限制下算法的改进进行修正。可见由于通过SRGCC算法可以获得更高的时间差估计分辨率，对于麦克风阵列，当采样率较低使用传统方法会导致定位发散时，本文方法可以精确定位到局部放电点附近；当采样率比较高时，采用本文方法也可以提高放电源定位精度。

5 结 论

针对传感器有限采样率条件下TDOA定位精度不足问题，本文提出一种突破传感器采样率限制的超分辨率SRGCC方法，能够对同源局部放电超声信号时间差进行更精确的估计。本文结合仿真给出了超分辨率时间差估计相关理论、流程及方法，比较了不同加权函数下的时间差收敛性能和该算法的抗噪能力，理论证明了其正确性和可行性。最后通过实验验证了本算法在实际局部放电定位中的适用性与准确性。本文主要研究成果如下：

1）提出超分辨率时间差估计算法，其在广义互相关理论支撑下应用信号阈值降低噪声的影响，通过在频域进行乘方操作扩展采样频率，并通过峭度分析选择合适的收敛次数，以实现超分辨率估计时间差。

2）通过仿真实验验证了SRGCC算法可精确地对时间差进行超分辨率估计，并选取不同加权函数分析其对SRGCC算法的影响，对比了各加权函数进行超分辨率时间差估计的收敛速度和精确度。

3）搭建局部放电定位实验平台，通过四元麦克风阵列采集局部放电超声信号，应用SRGCC算法进行局部放电源定位验证实验。结果表明，相比传统GCC算法，SRGCC算法的定位精度在各采样率下均有较大提高。

参 考 文 献：

［1］ 杨帆， 张玉琛， 王鹏博， 等. 电容屏破损缺陷局部放电过程规律特征及仿真分析[J]. 电工技术学报， 2024， 39（9）： 2860.

YANG Fan， ZHANG Yuchen， WANG Pengbo， et al.Characteristics and simulation analysis of partial discharge Process of condenser foil layer defect[J]. Transactions of China Electrotechnical Society， 2024， 39（9）： 2860.

［2］ 马世金， 王鹏， 朱英伟， 等. 变频电机匝间绝缘故障放电信号电磁辐射特性研究[J]. 电工技术学报， 2023， 38（22）：5975.

MA Shijin， WANG Peng， ZHU Yingwei， et al. Electromagnetic radiation characteristics of partial discharge in inverter-fed motor turn-turn insulation [J]. Transactions of China Electrotechnical Society， 2023， 38（22）：5975.

［3］ CAFFERY J J. A new approach to the geometry of TOA location[C]//Vehicular Technology Conference Fall 2000. IEEE VTS Fall VTC2000. 52nd Vehicular Technology Conference， September 24-28， 2000， Boston， MA， USA. 2000：1943-1949.

［4］ ZHU X， ZHU W， CHEN Z. Direct localization based on motion analysis of single-station using TOA[C]// 2018 2nd IEEE Advanced Information Management， Communicates， Electronic and Automation Control Conference （IMCEC）， May 25-27， 2018， Xi’an， China.2018：1823-1827.

［5］ WAX M， KAILATH T. Decentralized processing in sensor arrays[J]. IEEE Transactions on Acoustics， Speech， and Signal Processing， 1985， 33（5）：1123.

［6］ ZHENG Quanfu， LUO Lingen， SONG Hui， et al. A RSSI-AOA-based UHF partial discharge localization method using MUSIC algorithm[J]. IEEE Transactions on Instrumentation and Measurement， 2021， 70： 1.

［7］ LI Xinya， DENG Zhiqun， RAUCHENSTEIN L T， et al. Contributed review： source-localization algorithms and applications using time of arrival and time difference of arrival measurements[J]. The Review of Scientific Instruments， 2016， 87（4）：041502.

［8］ WANG Tao， WANG Dongying， PEI Yu， et al. Gas leak localization and detection method based on a multi-point ultrasonic sensor array with TDOA algorithm[J]. Measurement Science and Technology， 2015， 26（9）：095002.

［9］ 陈昊， 张楠， 高彩霞， 等. 永磁同步电机匝间短路故障短路线圈定位方法[J]. 电机与控制学报， 2023， 27（3）： 124.

CHEN Hao， ZHANG Nan， GAO Caixia， et al. Fault coil location approach of permanent magnet synchronous motor with interturn short circuit fault [J]. Electric Machines and Control， 2023， 27（3）： 124.

［10］ KNAPP C， CARTER G. The generalized correlation method for estimation of time delay[J]. IEEE Transactions on Acoustics， Speech， and Signal Processing， 1976， 24（4）：320.

［11］ YANG L， JUDD M D， BENNOCH C J. Time delay estimation for UHF signals in PD location of transformers[C]//The 17th Annual Meeting of the IEEE Lasers and Electro-Optics Society， October 20， 2004， Boulder， CO， USA.2004：414-417.

［12］ 唐炬， 陈娇，张晓星， 等. 用于局部放电信号定位的多样本能量相关搜索提取时间差算法[J]. 中国电机工程学报， 2009， 29（19）：125.

TANG Ju， CHEN Jiao， ZHANG Xiaoxing， et al. Time difference algorithm based on energy relevant search of multi-sample applied in PD location[J].Proceedings of the CSEE，2009，29（19）：125.

［13］ LI Tianrun， HU Rendan， ZHANG Zhibo， et al. A time delay estimation method of LFM hybrid signals based on hough transform[C]//2021 IEEE 5th Advanced Information Technology， Electronic and Automation Control Conference（IAEAC）， March 12-14， 2021， Chongqing， China. 2021：1457-1460.

［14］ 吴佳享， 孙云莲， 陈楚昭. 微弱行波下多分支配电网故障定位[J]. 电机与控制学报， 2023， 27（5）： 20.

WU Jiaxiang， SUN Yunlian， CHEN Chuzhao. Fault location of multiple branches distribution network under weak traveling waves[J]. Electric Machines and Control， 2023， 27（5）： 20.

［15］ ZHANG Huanhuan， CHEN Rushan. Coherent processing and super-resolution technique of multi-band radar data based on fast sparse bayesian learning algorithm[J]. IEEE Transactions on Antennas and Propagation， 2014， 62（12）： 6217.

［16］ SACHS J， PRYERL P， ZETIK R， et al. M-sequence ultra-wideband-radar： state of development and applications[C]//2003 Proceedings of the International Conference on Radar， September 3-5， 2003， Adelaide， Australia. 2003：224-229.

［17］ 汤林， 胡岳， 王红斌， 等. 基于插值相关法的局部放电特高频脉冲信号时延估计[J]. 高电压技术， 2015， 41（10）： 3320.

TANG Lin， HU Yue， WANG Hongbin， et al. Time-delay estimation of partial discharge UHF pulse signals based on interpolation cross-relation algorithm[J]. High Voltage Engineering， 2015， 41（10）： 3320.

［18］ 关宇， 董明， 席英杰， 等. 基于频域阈值处理广义互相关和空间筛选的多源局部放电定位方法[J]. 电网技术， 2024， 48（4）： 1721.

GUAN Yu， DONG Ming， XI Yingjie， et al. Multi-source partial discharge localization method based on frequency domain threshold processing generalized cross-correlation and spatial screening[J]. Power System Technology， 2024， 48（4）： 1721.

［19］ 罗日成， 李卫国， 李成榕， 等. 基于改进PSO算法的变压器局部放电超声定位方法[J]. 电力系统自动化， 2005，29（18）： 66.

LUO Richeng， LI Weiguo， LI Chengrong， et al. Ultrasonic localization of partial discharge in power transformer based on improved particle swarm optomozation[J]. Automation of Electric Power Systems， 2005，29（18）： 66.

（编辑：邱赫男）