求解非凸正则化问题的 L-BFGS 算法
2024-01-26陈鸿升叶建豪胡子健程万友
陈鸿升,叶建豪,胡子健,程万友
(东莞理工学院 计算机科学与技术学院,广东 东莞 523808)
0 引言
本文将考虑以下模型:
minφ(x):=f(x)+r(x),
(1)
式中,f:Rn→R为连续可微的函数.问题(1)的一个重要应用形式是压缩感知问题:
(2)

求解l0问题的一般做法是将问题转化为凸l1问题.常见的用来求解l1问题的算法有:迭代收缩阈值算法(ISTA)[2-3]、内点法[4]、投影梯度法[5]、交替方向乘子法和可分离增广拉格朗日收缩算法(split augmented Lagrangian shrinkage algorithm,SALSA)[6]、约化空间算法[7]、坐标下降方法[8]、积极集方法[9]等.
为了克服l1罚函数的弊端,人们提出了许多非凸非光滑的罚函数.如 log-sum[10]、cappedl1[11]、lp[12-13]、SCAD[14]、MCP[15]等.这些罚函数被证明比l1罚函数具有更好的稀疏性,且能降低大系数的偏差估计[14,16].人们提出了一些求解这些罚函数的方法,第一类是运用光滑技术的方法,如:光滑序列二次规划(SQP)和光滑信赖域牛顿方法(TRN)[13]用来求解包含lp、SCAD 和 MCP 问题在内的一类非凸非光滑问题;第二类方法是迭代重加权最小化算法[10,14-15],这类算法通过求解一系列的l1子问题或l2子问题来实现问题的求解,但这类方法所生成序列的收敛性通常是不明确的;第三类方法基于 CD规划思想.文献[17]中提出了一种通用的 ISTA 算法,并在 SCAD、MCP 和 cappedl1罚函数上进行了说明,证明了该算法能收敛到稳定点.更多方法,请参考文献[18-19].
有限内存的拟牛顿方法(L-BFGS)收敛速度快,而且仅需要贮存最近的m个n维向量对形成Hessian 逆的估计,并且不需要贮存矩阵,被认为是求解大规模优化问题[20-21]的最有效方法之一.本文利用文献[1]的积极集识别技术和 L-BFGS 算法提出一种求解大规模l1、SCAD 和 MCP 问题的 L-BFGS 算法.在积极集集合上算法的搜索方向与文献[1]的方向相同,自由空间集合上使用了 L-BFGS 的搜索方向.在适当的条件下,证明了使用非单调技术[22]的算法是全局收敛的.数值实验证明提出的算法是有效的.
1 预备知识
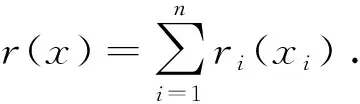
τ>1时,问题(1)为 MCP 问题;当
τ>2时,问题(1)为 SCAD 问题.
为定义新算法的搜索方向,将B(x) 划分为4部分:
B11(x)={i:0
B13(x)={i:-λ≤xi<0,xi-gi(x)<-λ},B14(x)={i:-λ≤xi≤0,xi-gi(x)>λ}.
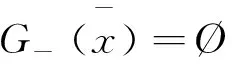
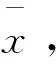
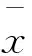
特别的,
L-BFGS 算法收敛速度快,而且仅需要贮存最近的m个n维向量对形成 Hessian 逆的估计,并且不需要贮存矩阵,被广泛应用于求解无约束和约束优化问题[20-21].本文中采用文献[20]的方法得到问题(1)的 Hessian 逆的估计H(k),即:
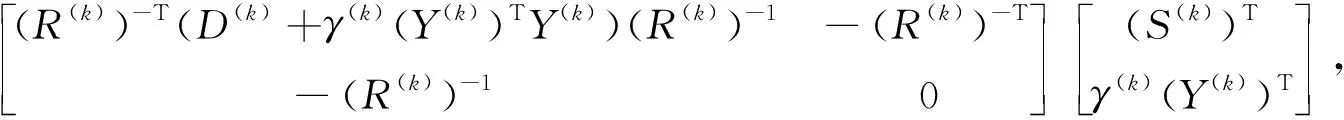
(3)
式中:γ(k)>0;s(k)=x(k+1)-x(k);y(k)=g(x(k+1))-g(x(k));S(k)=[s(k-m),…,s(k-1)];
D(k)=diag[(s(k-m))Ty(k-m),…,(s(k-1))Ty(k-1)].
2 新算法
本节中,将利用文献[1]的积极集识别技术和 L-BFGS 算法,提出一种求解大规模l1、SCAD 和 MCP 问题的 L-BFGS 算法.设式(1)中的目标函数满足以下假设.
假设2.1
1)水平集 Θ:={x∈Rn:φ(x)≤φ(x(0))} 有界.
2)存在Θ 的一个邻域N,使得f是二阶可微的函数,且f的一阶导数满足 Lipschitz 连续性.即存在常数L>0,使得
‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈N
成立.
2.1 搜索方向的计算及性质


(4)
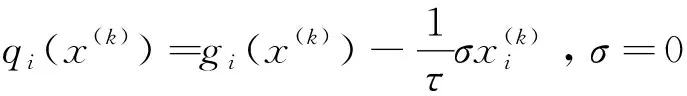
2.2 搜索方向的计算及性质
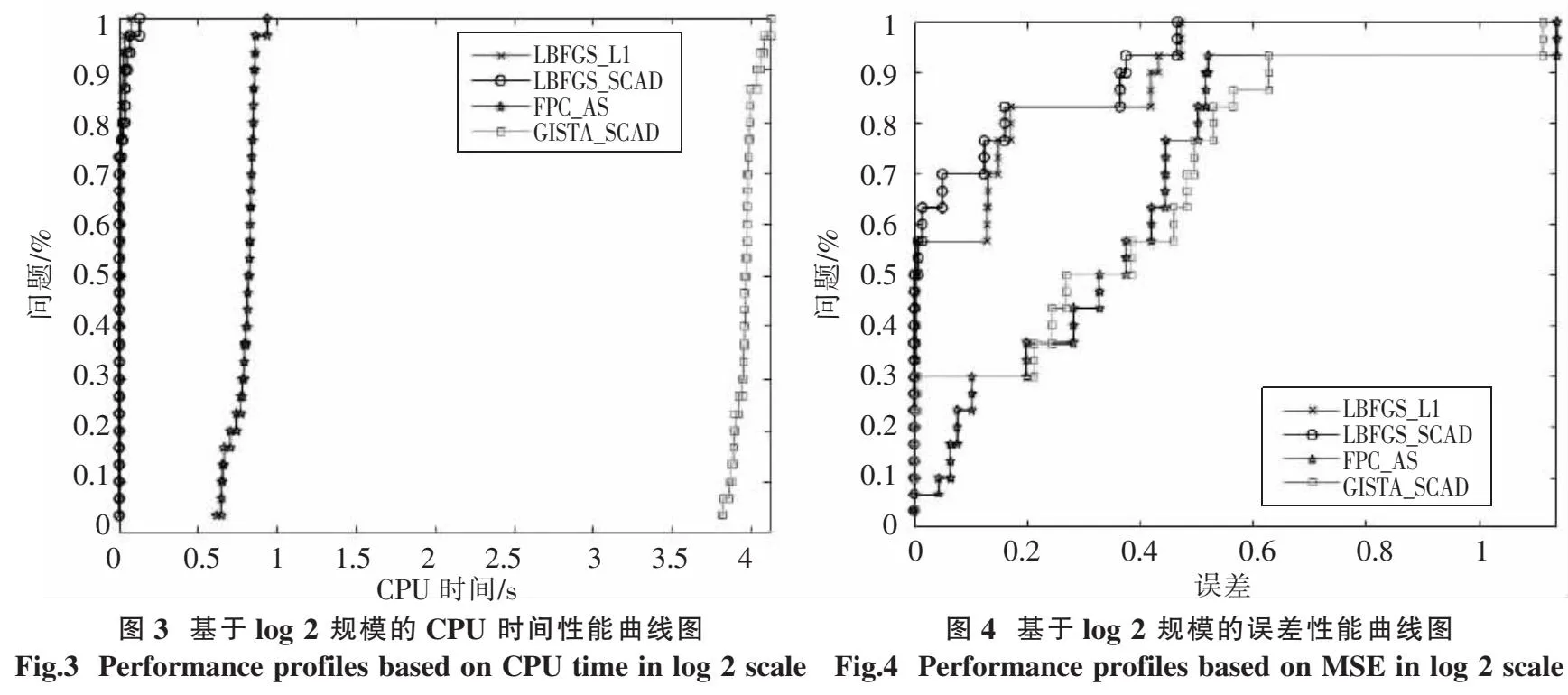
对任意k,存在 0 (5) 成立. 利用柯西不等式结合式(5)得到 (6) 引理 2.1设假设 2.1和假设 2.2成立,d(k)由式(4)定义,则有 成立. 引理2.2设假设 2.1和假设 2.2成立,d(k)由 式(4)定义,则有d(k)=0 当且仅当x(k)为式 (1)的一个稳定点. 引理 2.3设假设 2.1和假设 2.2成立,d(k)由 式(4)定义,β∈(0,1],则有 和 成立.式中,σ=0 对应于l1问题和 SCAD 问题,σ=1 对应于 MCP 问题. 下面的定理表明,若x(k)不是式 (1)的一个稳定点,则d(k)为φ(x) 在x(k)处的下降方向.该定理保证了算法 2.1是正确定义的.由于定理的证明相似于文献[1]的引理 4.1,此处省略. 定理 2.1设假设 2.1和假设 2.2成立,d(k)由 式 (4)定义.若d(k)≠0,则有 下面给出新算法的详细步骤. 算法2.1 L-BFGS 拟牛顿法 输入:x(0)∈Rn、γ,η,δ∈(0,1),C(0)=φ(x(0)),Q(0)=1,k:=0. 输出:最终解xk、最终函数值φ(xk)、迭代次数k. 1.若满足终止条件,则终止算法. 2.通过式(4)计算d(k). 3.计算β(k)=max{ηj:j=0,1,…} 满足φ(x(k)+β(k)d(k))≤C(k)-δ(β(k)‖d(k)‖)2. (7) 4.计算x(k+1)=x(k)+β(k)d(k). 5.计算Q(k+1)=γQ(k)+1,C(k+1)=(γQ(k)C(k)+φ(x(k+1)))/Q(k+1). (8) 6.设k:=k+1.转到步骤1. 在步骤 3 中,采用非单调线性搜索技术,与文献[22]的公式 (7)相同,通过公式(8)对C(k)进行更新.与文献[1]中的算法相比,在d(k)的计算上采用了 L-BFGS算法,这使得文中的算法能够适用于大规模问题的求解. 引理2.4设假设 2.1和假设 2.2成立,{x(k)} 为算法 2.1产生的序列,则有 (9) 成立. 证明因为 0<γ<1,由式(8)和Q(0)=1 得到 (10) 由式(10)及式(7)和式(8)得到 (11) 因此{C(k)} 是单调递减的.进一步由线性搜索式(7)得到 {x(k)}⊂Θ.由假设2.1的1)得到 {C(k)} 有下界,因此 {C(k)} 是收敛的.对式(10)两边求和,利用 {C(k)} 的收敛性得到结论. 接下来的引理 2.5 和定理 2.2表明,{x(k)} 的每一个聚点均为问题 (1)的稳定点.由于引理 2.5的证明相似于文献[1]的引理 4.5,此处省略. 引理 2.5设假设 2.1和假设 2.2成立,d(k)由式(4)定义.若x(k)→x*,d(k)→0,则x*为问题(1)的一个稳定点. 定理2.2设假设 2.1和假设 2.2成立,{x(k)} 为算法 2.1产生的序列,则 {x(k)} 的任一聚点x*均为问题(1)的稳定点. 证明由于 {x(k)}⊂Θ,且水平集 Θ 有界,因此 {x(k)} 至少存在一个聚点.假设x*为 {x(k)} 的任意一个聚点,则存在一个无限集合K使得 考虑以下两种情况. (12) 成立.由中值定理可知,当k∈K足够大时,有下式成立, 其中,τ(k)∈(0,1).将式(12)带入最后一个不等式,可得 本节中用数值实验来测试提出的新算法,并将新算法与 GIST 算法[17]和 FPC_AS算法[23]进行比较.GISTA 和FPC_AS的代码可以找到.分别用 GISTA_SCAD 和 GISTA_MCP 表示代码 GISTA 的 “SCAD” 和 “MCP” 形式.实验的代码通过 MATLAB R2018a 编写,并在一台搭载有Windows 10 系统的 PC 上运行 (CPU:i5-6300HQ,内存:16G).所有参数都使用默认值,初始点均为零向量. 将算法应用于压缩感知式 (2).其目标是从m个观测数据中,重构出一个长度为n的稀疏信号(m 其中ε=‖e‖. 本节中取n=215,m=round(0.1×n),xs中非零元素个数为T=1,2,…,50.“CPU time” 表示以秒为单位的 CPU 时间,“err” 表示误差(err=‖x*-x(k)‖∞). 为了更直观地展示数值实验的结果,文中采用文献[24]中所描述的性能曲线图,将数值结果中的 “CPU time”“err”分别用图1~图4进行展示.从图1~图4可以看出,GISTA_SCAD 和 GISTA_MCP 总是需要花费更多的 CPU 时间;GISTA_SCAD、GISTA_MCP 和 FPC_AS 具有相近的误差.在大多数问题中,LBFGS_L1、LBFGS_SCAD 和 LBFGS_MCP 花费的 CPU 时间更少,且具有更小的误差. 本文基于文献[1]的积极集识别技术和 L-BFGS 算法,提出了一种用于求大规模l1、SCAD 和 MCP 问题的新方法.在适当条件下,证明了新方法在采用非单调线性搜索时的全局收敛性.数值实验证明了新方法对于求解大规模l1、SCAD 和 MCP 问题具有优秀的性能.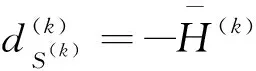
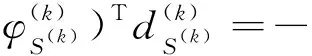
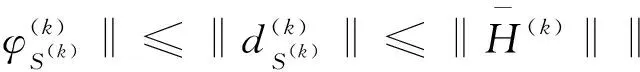
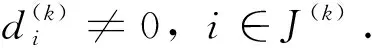
2.3 算法及其收敛性
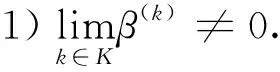
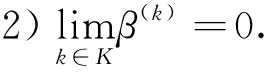
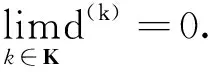
3 数值实验


4 总结
