DNA存储场景下的大小喷泉码模型设计*
2024-01-24崔竞松蒋昌跃
崔竞松,蒋昌跃,郭 迟
(1.武汉大学国家网络安全学院,湖北 武汉 430072;2.武汉大学空天信息安全与可信计算教育部重点实验室,湖北 武汉 430072; 3.武汉大学卫星导航定位技术研究中心,湖北 武汉 430072)
1 引言
据估计,到2025年全球数据总量将达163 ZB,而当前主流存储介质的生产已不堪重负[1,2]。DNA是生物体用于存储遗传信息的载体,同样具有存储数字信息的能力。研究表明,DNA信息存储密度可以达到1019bit/cm3,是硬盘的106倍[3,4]。DNA作为数据的存储介质,具有密度大、能耗低、寿命长等优点,因此DNA存储有广阔的应用前景[5]。
目前已经提出了多种DNA存储方案。2012年哈佛大学的Church等人[6]利用二进制转换首次实现在体外将659 KB的数据存储进DNA分子中,但该方案引入的冗余过多。2013年Goldman等人[7]利用哈夫曼编码、四倍重叠法、三进制编码将739 KB的信息存入DNA中。2015年Grass等人[8]将RS(Reed-Solomon)纠错应用于DNA存储,实现了83 KB信息的无错误存储和读取。2016年Blawat等人[9]将“前向纠错码”引入DNA存储领域,提升了使用DNA分子进行数据存储的可靠性。同年Bornholt等人[10]设计实现了DNA存储体系中数据的“随机访问”。2017年哥伦比亚大学的Erlich等人[11]将“喷泉码”引入到DNA编码体系中,称之为“DNA喷泉”,实现了较高的数据存储密度,降低了冗余和成本。2020年Koch等人[12]将喷泉码运用于信息存储,并提出了“DNA信息可存储万物”的概念DoT(DNA-of-Things)。
过往研究中使用的喷泉码算法在DNA存储等应用场景中存在一定的不足:编码端将源文件划分成K个分组进行编码,而解码端需要确定参数K值才能进行解码,因此在编码端与解码端之间需要额外的信道资源来传递关键参数K。在实际应用中可将K直接嵌入到所有编码分组中来进行传递。但是,这种做法有极大的冗余,严重浪费信道的带宽。另一种做法是在编码端和解码端中将K设为固定值。但是,这种做法忽略了源文件大小、数据分组长度及数据分组数目之间的关系,不适用于实际的DNA存储应用场景。
基于上述问题,本文以DNA存储应用为背景,提出了一种大小喷泉码模型。一方面大喷泉码用来编码存储源文件的内容;另一方面通过增加小喷泉码带外信道来优化关键参数K的传递,提高了带宽的利用率,同时K可取任意值,摆脱了源文件大小等的限制。大喷泉码与小喷泉码互相结合,共同实现对源文件的编码存储。
2 喷泉码与LT码
喷泉码是一种纠删编码[13-16],最初是针对二进制删除信道BEC(Binary Erasure Channel)设计的,旨在为大规模数据的传输和可靠广播场景提供一种理想的解决方案。在DNA存储场景下,DNA分子在保存和复制的过程中会发生一定概率的变异甚至片段丢失。由于变异或片段丢失的DNA分子不可再用,相当于丢弃了数据,因此DNA分子存储是一个典型的删除信道。
LT码(Luby Transform codes)是由Luby[17]在2002年提出的第一种实用喷泉码。LT码是一种无速率码,可产生无限的编码数据,具有简单的编译码方法、较小的译码开销和编译码复杂度。LT码将源文件转换为大量较短的信息,这些较短的信息并非源文件的一部分,而是将源文件中的信息通过特定的方式进行运算编码后产生的。接收端收到一定量以上的编码数据就可能成功解码,与收到哪些编码数据无关。
2.1 LT码度分布
度是指与某一编码数据分组相关联的原始数据分组的数目,通常用d表示。传统LT码的度分布函数是由Luby首先提出来的理想孤波分布[17],其表达式如式(1)所示:
(1)
在实际应用中,编码数据的抽样往往无法精确符合理想孤波分布,总存在一些波动和误差,从而出现解码时度为1的数据断层,导致解码失败。所以,通过修正理想孤波分布,给出更实用的鲁棒孤波分布[18],其表达式如式(2)所示:
(2)

(3)
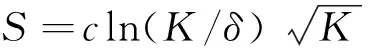
2.2 LT码编码
设有K个待编码的原始数据分组,LT码的编码算法如算法1所示。
2.3 LT码解码
LT码解码是对接收到的N(N≥K)个编码数据进行处理,从中恢复出K个原始数据。传统LT码解码算法通常采用复杂度较低的置信度传播BP(Belief Propagation)算法,其平均时间复杂度为O(KlnK)。该算法主要是从接收端生成的二分图中,通过信息在校验节点与变量节点之间不断流动消去无用的边,最终恢复出K个变量节点的值。传统LT码解码算法如算法2所示。
BP解码算法的双向图解码过程如图1所示。
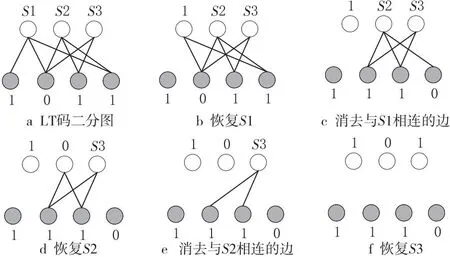
Figure 1 Process of LT code decoding图1 LT码解码过程
图1展示了从编码数据{1011}恢复出原始数据{101}的过程,其中空心圆表示原始数据分组,实心圆表示编码数据分组。
2.4 使用喷泉码算法的DNA存储框架
使用喷泉码进行DNA存储的框架主要包括3个部分:源文件编码写入、介质生化存储和解码获取源文件。
源文件编码写入是利用喷泉码编码算法将源文件转换成若干条等长的DNA序列。介质生化存储是将源文件编码生成的DNA序列进行生化处理,主要包括DNA分子合成及DNA分子储存。解码获取源文件是从DNA分子中还原出源文件,是编码写入的逆过程。在解码之前,需要先对DNA分子进行生化实验预处理,包括:PCR(Polymerase Chain Reaction)序列扩增、DNA测序(分析特定DNA片段的碱基序列,获取DNA序列的A,C,G,T排列方式),再进行DNA序列纠错、DNA序列去重等操作,最后进行喷泉码解码,获取源文件。使用喷泉码算法的DNA存储编解码过程如图2所示。
3 面向DNA存储的大小喷泉码
3.1 DNA存储场景的局限性
知名DNA合成公司TWIST目前的二代合成芯片高通量合成的寡核苷酸池(DNA文库)中,单条DNA序列的碱基最大个数仅为300[19]。DNA序列合成技术的限制使得用户在进行存储编码之前就需要确定出编码输出DNA序列的长度及条数。
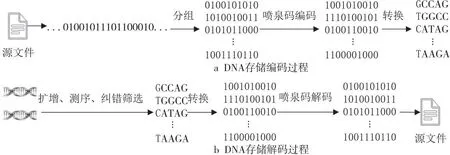
Figure 2 DNA encoding and decoding using fountain code algorithm图2 使用喷泉码算法的DNA编解码
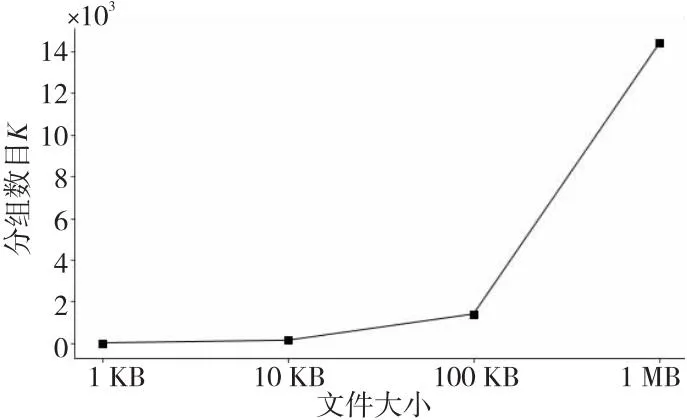
Figure 3 File size varying with K value图3 文件大小随K值的变化情况
目前普遍使用四进制方式编码DNA序列,即按照{00,01,10,11}与{A,C,G,T}的对应关系来实现二进制数据与DNA序列之间的转换。DNA序列长度的限制会影响编码时源文件数据分组长度的划分,从而会导致参数K有较大变化。例如,当规定喷泉码编码输出的单条DNA序列碱基个数为300时,编码4个文件,大小分别为1 KB,10 KB,100 KB和1 MB的文件,编码端将源文件划分成的数据分组数目K随文件大小变化的情况如图3所示。
从图3可以看出,当都按照300碱基长度进行数据分组时,参数K会随文件长度的增大而明显变化。若在编码端和解码端将K设为定值,则会影响源文件数据分组的长度,进而影响编码数据转换成的DNA序列的长度,显然不适合DNA存储的应用场景,因此有必要将参数K的信息传递给解码端。
3.2 小喷泉码设计
设源文件的比特数为L,源文件划分的原始数据分组比特数为l,则K的计算如式(4)所示:

(4)
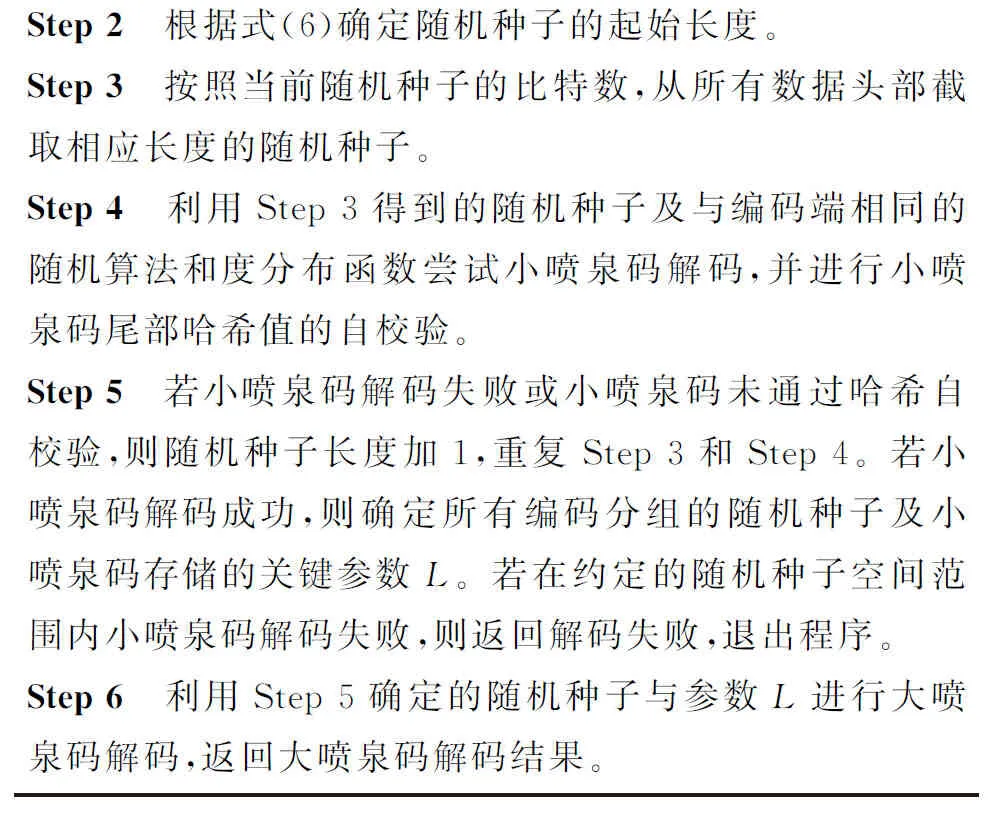
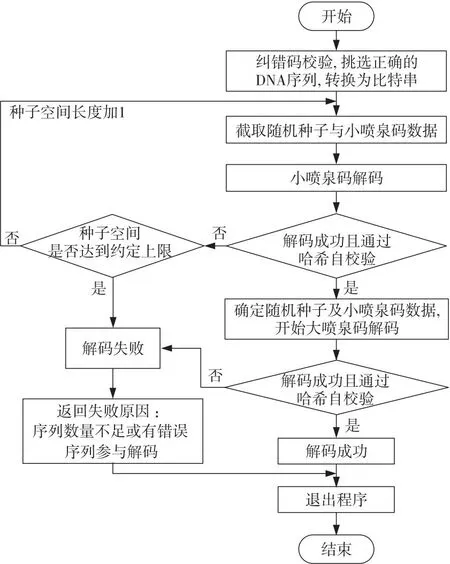
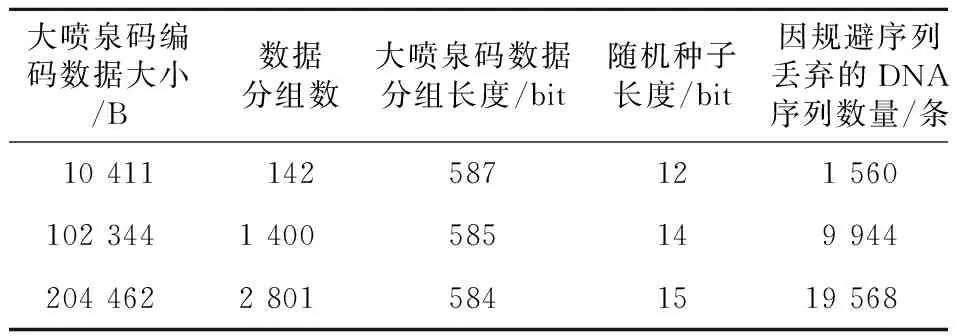
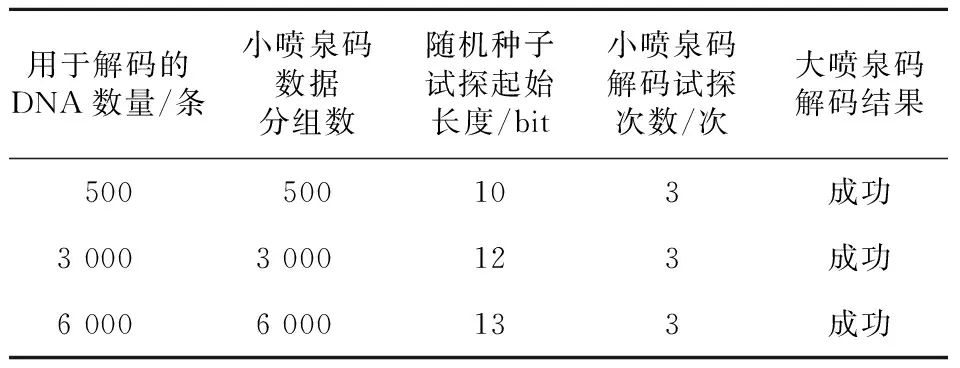
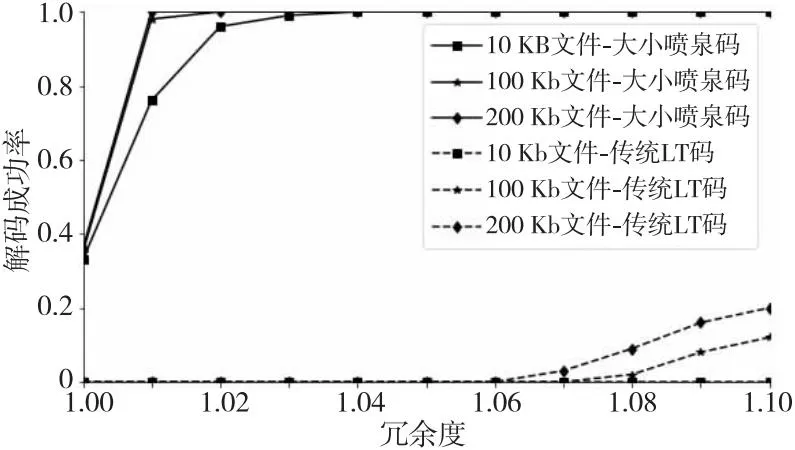
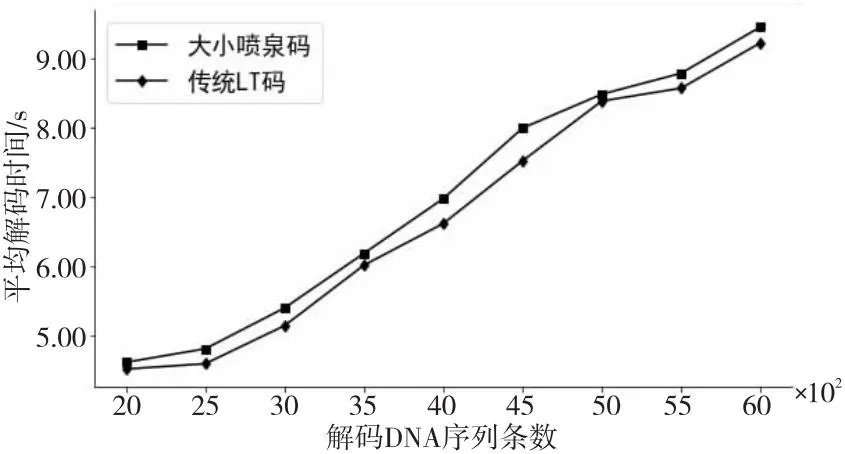
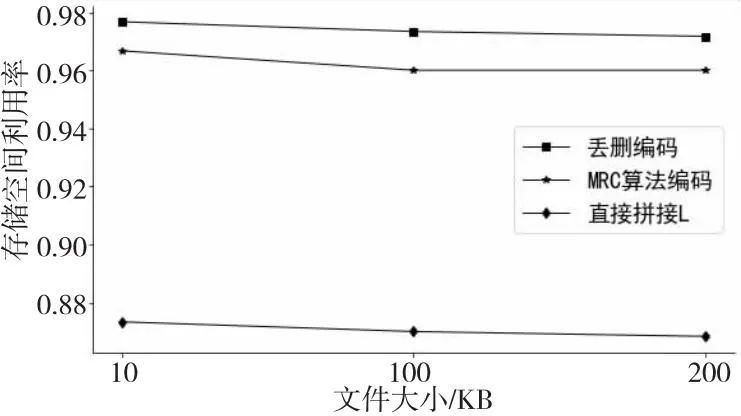
当L不能被l整除时,表示划分的最后一个数据分组不足l比特,需要将其填充为l比特。设最后一个数据分组填充的比特数为n(0≤n n=K×l-L (5) 解码端利用四进制编码将接收到的DNA序列还原成二进制数据即可得知数据分组的比特数l。解码端只要再获取源文件的比特数L,即可由式(4)和式(5)计算出解码所需要的关键参数K和n。所以,要将源文件的比特数L传递给解码端。 设编码端和解码端将参数L统一用64 bit的整型表示。如果直接将L拼接在每个编码数据分组的末尾,则解码端从接收到的数据末尾截取固定的64 bit即为L。这种做法简单有效,但会严重浪费信息空间,所有数据分组都拼接相同的64 bit信息会造成极大的冗余。解码端只要成功收到一个数据分组即可获得参数L,而其它数据分组末尾的64 bit将全部失去价值。 为了尽量减少参数L的带宽,为大喷泉码留出更多的数据存储空间,本文设计了小喷泉码来对参数L的传输进行优化。 大小喷泉码使用了一大一小2个喷泉码对同一个源文件的不同信息分别进行编码,再将2个喷泉码的编码结果合并为一个编码分组进行存储和传输,模型结构如图4所示。 3.3.1 大喷泉码编码内容 如图4上半部分所示,大喷泉码负责对源文件的内容进行编码。编码端读取待存储的源文件后,按照LT码编码算法(算法1)的步骤进行编码。 Figure 4 Coding structure of big and small fountain code model图4 大小喷泉码模型编码结构 为了在解码时能百分之百还原出存储的源文件,大喷泉码编码的数据中还包含了源文件的名字及一个哈希值。先将固定长度的文件名拼接在源文件内容之后,再整体生成一个固定长度的哈希值并拼接在最后。将拼接了文件名和哈希值的数据作为源数据输入大喷泉码模型进行编码。哈希值用于自校验解码出的内容与编码时的内容是否相同。模型中编码端与解码端约定文件名与哈希值分别是相同的固定字节长度,这样解码端在解码出数据后,从尾部截取固定长度即可获得哈希值与文件名。 大喷泉码将拼接了文件名和哈希值的源数据划分为若干等长且互不重叠的数据分组,再利用随机种子和度分布函数生成度值,最后选择相应的数据分组进行异或运算,源源不断地产生编码分组。 3.3.2 小喷泉码编码内容 如图4的下半部分所示,小喷泉码负责对大喷泉码编码数据的比特数L进行编码。与大喷泉码相同,小喷泉码在对参数L编码之前,先对其生成一个固定比特数的哈希值,再将哈希值拼接在参数L的末尾。哈希值同样用来自校验,确保解码出的数据与编码时的相同。 小喷泉码编码数据划分成的分组长度相对较短,一般为1 bit,也可根据具体场景进行调整。小喷泉码编码数据的比特数固定,因此总被划分为固定数量的分组,再按照算法1的步骤进行编码。大喷泉码与小喷泉码编码同一个数据分组时,使用同一个随机种子及度分布函数进行独立编码。在实际应用中,编码输出的DNA序列数量通常远大于小喷泉码编码的原始数据分组数,因此小喷泉码数据具有足够大的冗余可以保证编码存储的信息能被解码端成功解码。 无论大喷泉码还是小喷泉码,都保留了传统喷泉码应对丢删错误的特性,即在有部分数据随机丢失的情况下都能从剩余编码数据中恢复出原始数据。 在DNA序列合成与测序过程中,由于生化实验上的限制,并非所有编码生成的DNA序列都可用,如GC含量高、均聚物长(如AAAAAA…)或含有酶切位点的DNA序列是不可取的,因为它们很难合成且容易出现测序错误[20,21]。为了保证编码数据转换成的DNA序列能够满足生化实验上的要求,在编码输出序列时要考虑DNA规避序列的限制。如何避免规避序列的影响,本文基于大小喷泉码提供了2种编码方案。 4.1.1 丢删编码 喷泉码主要应用在删除信道场景中,其良好的特性能保证即使在有数据丢失的情况下,只要收集到足够数量的数据,依然有很高的概率能成功解码。因此,当编码生成的DNA序列中出现了需要规避的子序列时,可直接将该条序列丢弃。喷泉码可以生成无限数量的编码数据,丢弃部分数据不会对编解码过程产生影响。 该方案操作简单,但当规避序列需要丢弃大量序列时,会导致随机种子的比特空间有较大的膨胀。例如,当需要编码输出1 000条DNA序列时,在无规避序列的情况下只需10 bit的种子空间;而当规避序列特别多或需要规避一些出现频率较高的子序列时,可能至少需要生成100 000条序列才能产生1 000条合格的序列,而此时随机数种子的空间就变为了17 bit,这会导致原本存放大喷泉码编码数据的带宽被占用。 4.1.2 MRC算法编码 编码端可采用一些编码算法,在将编码数据转换成DNA序列时直接规避掉不希望出现的子序列,例如Liu等人[22]提出的MRC(Mixed Radix Coding)算法。MRC算法不是利用四进制方式编码DNA序列,而是利用变进制的思想,在把编码数据转换成DNA序列的过程中,结合用户输入的规避序列,通过不断地进行取模、除法操作直接生成不含规避序列的DNA序列。该算法的优点是编码端不会因规避序列而大量丢弃生成的DNA序列,一旦产生足够数量的序列即可结束编码;缺点是DNA存储介质的不均匀性会导致MRC算法编码出的DNA序列是不定长的。超过长度的DNA序列会被丢弃,因此为了保证大多数MRC算法转化的序列长度小于或等于规定的长度,需要适当地缩短源文件划分数据分组的比特数l。 对于MRC算法编码生成的长度小于规定长度的DNA序列,需要将末尾的间隙进行填充,使得所有序列保持等长。为了充分利用部分碱基序列尾部的间隙空间,可利用小喷泉码的编码数据进行填充。这种方案下小喷泉码需在大喷泉码编码之后再进行编码。在将大喷泉码编码数据使用MRC算法编码成DNA序列之后,统计该序列缺损的碱基空间数,此时小喷泉码再利用大喷泉码的随机种子编码出相应数量的数据进行填充。 2种方案编码生成的数据分组结构示意图如图5所示。 Figure 5 Encoded packet structures of two schemes图5 2种方案的编码分组结构 图5a为丢删编码方案的分组结构示意图,其特点是所有数据分组中的大喷泉码数据及其对应的DNA序列都是等长的;所有分组最后固定的1 bit为小喷泉码数据,小喷泉码编码数据量等于总编码分组数量。图5b为MRC算法编码方案的分组结构示意图,其特点是所有数据分组中的大喷泉码数据是等长的,但转换成的DNA序列是不定长的;对那些长度较短的DNA序列利用小喷泉码数据进行填充使其都变为等长的,小喷泉码编码数据与总分组数目之间的关系不固定。 喷泉码编码出的每个数据分组都有一个唯一对应的随机数种子。解码端使用与编码端相同的随机算法,即可根据随机种子恢复出编码数据的度及参与编码的原始分组编号等信息,因此随机种子也需要随编码数据一起传递给解码端。 由于编码文件的大小不固定,或用户对同一文件有不同的编码DNA序列长度、数量要求时,会导致随机种子的比特空间有较大变化。例如,将同一个文件编码成500条DNA序列,只需9 bit的种子空间,而编码成10 000条序列至少需要14 bit的种子空间。为了充分利用有限长度的DNA序列中的所有空间,大小喷泉码模型将编码数据中的随机数种子设计为动态长度的形式进行嵌入。 以丢删编码方案为例,模型按照实际需求计算出一个确定长度的随机种子直接拼接在编码数据分组的头部,尾部的1 bit存放小喷泉码编码数据,中间剩余的空间全部存放大喷泉码的编码数据。对于输入的源文件,编码端进行填充、拼接文件名、生成哈希值等预处理后,大喷泉码与小喷泉码获得各自待编码的数据,结合用户输入的规避序列及DNA序列长度和数量要求,开始进行编码。以丢删编码方案为基础的大小喷泉码模型的编码算法如算法3所示。 算法3 大小喷泉码编码算法输入:源文件。输出:指定长度和数量的DNA序列。Step 1 读取源文件,对待编码数据进行填充、生成哈希值等预处理。Step 2 从根据实际要求计算得出的随机种子空间中产生一个随机种子。Step 3 大、小喷泉码分别利用Step2产生的随机种子各自进行编码。Step 4 编码端将随机种子与大、小喷泉码编码数据拼接后的数据转换成DNA序列。Step 5 检查生成的DNA序列中是否出现规避序列,出现则丢弃该条DNA序列,否则保留该条DNA序列。Step 6 重复Step 2~Step 5,若产生足够数量的DNA序列,则编码结束;若种子空间用完还未编码出足够数量的序列,则种子空间长度加1,重复Step 2~Step 6。 模型编码算法的流程如图6所示。 Figure 6 Flow chart of big and small fountain code encoding algorithms图6 大小喷泉码编码算法流程图 喷泉码要求用于解码的数据必须是无错的。在实际应用中,还需对喷泉码编码生成的DNA序列添加纠错码用于检错和纠错。在解码前先利用纠错编码挑出所有无错数据。获得无错数据后,解码第一步要先确定所有数据分组对应的随机种子。 模型编码时随机种子以动态长度的方式嵌入,但整个编解码过程中并未传递随机种子长度信息。大小喷泉码模型在解码端通过试探的方式,利用小喷泉码编码数据末尾哈希值的自校验来确定随机种子的长度。小喷泉码编码的数据比特数是固定值,因此被划分为固定数量个原始分组,记为k。解码端每次都先试探解码固定数量的k个小喷泉码数据,并进行哈希自校验确认是否解码成功,若解码失败则种子空间加1后重新试探。试探的过程不能无限进行下去,因此编码端和解码端需要约定好随机种子比特数的下限值llower和上限值lupper,则编码端能够编码的DNA序列总数被限定在了[2llower,2lupper]内。假设试探随机种子的起始长度为seedlenstart,解码端接收到的DNA序列数量为N(N≥K),则式(6)成立: seedlenstart=max(llower,lbN+1) (6) 从式(6)可以看出,从随机种子长度的下限值及根据N计算得出的随机种子长度中选择较大值作为起始值开始试探。大小喷泉码模型的解码算法如算法4所示。 算法4 大小喷泉码解码算法输入:DNA序列。输出:源文件。Step 1 利用纠错码挑选正确的DNA序列,将DNA序列按照对应方式转换成二进制数据,从所有编码分组数据尾部截取固定比特作为小喷泉码数据。Step 2 根据式(6)确定随机种子的起始长度。Step 3 按照当前随机种子的比特数,从所有数据头部截取相应长度的随机种子。Step 4 利用Step 3得到的随机种子及与编码端相同的随机算法和度分布函数尝试小喷泉码解码,并进行小喷泉码尾部哈希值的自校验。Step 5 若小喷泉码解码失败或小喷泉码未通过哈希自校验,则随机种子长度加1,重复Step 3和Step 4。若小喷泉码解码成功,则确定所有编码分组的随机种子及小喷泉码存储的关键参数L。若在约定的随机种子空间范围内小喷泉码解码失败,则返回解码失败,退出程序。Step 6 利用Step 5确定的随机种子与参数L进行大喷泉码解码,返回大喷泉码解码结果。 大小喷泉码模型解码算法流程如图7所示。 Figure 7 Flow chart of big and small fountain code decoding algorithm图7 大小喷泉码解码算法流程图 大喷泉码解码成功后,从解码出的数据末尾截取与编码端约定长度的比特数作为哈希值,并进行自校验。通过自校验后再从尾部截取固定的字节长作为文件名,再将剩余的数据全部写入到文件中进行保存,即恢复出了存储的源文件。 为了提高解码的成功率,大小喷泉码模型的解码算法均使用了置信度传播-最大似然联合译码BPML(Belief Propagation-Maximum Like-Lihood)算法[23]。解码时使用BP算法,利用1度的数据先进行线性解码。BP算法平均时间复杂度较低,消耗资源少,可快速解码出大部分的源数据。对那些因缺少1度数据而无法继续解码的剩余数据,解码端再使用最大似然(ML)解码算法,利用高斯消元求解方程组解码剩余数据,从而有效提高解码成功率。但是,ML算法的时间复杂度比较高,达到了O(K3)。 以存储图像为例,将图像分别压缩至10 KB, 100 KB和200 KB 3种大小进行DNA存储仿真实验。测试程序用C语言编写。 实验中设置随机种子比特数的下限为10,上限为24,因此编码端能够编码的DNA序列数被限制在[1 024,16 777 216]内,满足实验及应用的需求。设置式(3)中的参数c=0.05,δ=0.05。在假设规避序列只有{GGATCC,AAAA}的情况下,以输出300个碱基长的DNA序列为标准,对4.1节中提出的2种规避序列编码方案进行测试。3幅图像的编码要求信息如表1所示。 Table 1 Coding experiment information表1 编码实验信息 对4.1节提出的2种方案分别进行编解码实验。实验中设置编码端和解码端约定的文件名长度固定为100 B,哈希值长度固定为16 B,因此大喷泉码实际编码的数据为源文件内容再加上100 B的文件名和16 B的哈希值。模型中编码端和解码端都设置参数L为64 bit的整型表示。小喷泉码实际编码的是一个192 bit数的数据,其中包括64 bit的L和128 bit的哈希值,因此小喷泉码数据总是被固定地划分为192个分组。 5.1.1 丢删编码方案实验 丢删编码方案对3幅不同大小的图像进行编码时产生的数据如表2所示。 Table 2 Experimental results of drop-and-delete encoding 表2 丢删编码方案编码实验结果 表2中的大喷泉码数据分组长度为源文件内容划分的分组长度;随机种子长度是基于规避序列丢弃情况编码所需的DNA序列而确定的实际比特数。3幅图像在编码时被划分成的原始数据分组数K分别为142,1 400和2 801,而编码输出的DNA序列数都远高于原始数据分组数,其冗余率分别为604.2%,328.6%和328.4%,可以保证在有部分数据丢失的情况下依然具有较高的解码成功概率。 模拟DNA分子在复制、存储、测序时因变质而丢失的过程,即对3幅图像编码产生的DNA序列随机删除其中50%的数据,用剩余的数据进行解码,重复100次实验。3个样本剩余的用于解码的DNA序列数量分别为500,3 000和6 000,此时冗余率分别为252.1%,114.3%和114.2%。解码过程产生的数据如表3所示。 Table 3 Experimental results of drop-and-delete decoding 表3 丢删编码方案解码实验结果 由表3可知,利用式(6)计算3幅图像的随机种子试探的起始长度分别为10 bit, 12 bit和13 bit,小喷泉码试探解码的次数均为3次,大喷泉码的解码结果均为成功。 5.1.2 MRC算法编码方案实验 使用MRC算法编码方案测试时,为了保证大多数编码生成的DNA序列长度小于或等于规定的长度,对源文件的数据分组长度进行了适当的压缩,编码过程产生的数据如表4所示。 Table 4 Experimental results of MRC algorithm encoding 表4 MRC算法方案编码实验结果 由表4可知,该方案比丢删编码方案中的大喷泉码数据长度平均短8 bit,但平均丢弃的DNA序列数仅为丢删编码方案的0.8%。丢弃序列的减少降低了随机种子的比特长度,该方案比丢删编码方案的随机种子长度平均短了1 bit。 与丢删编码方案做法相同,从3幅图像编码生成的DNA序列中,随机删除50%的数据,用剩余的DNA序列分别进行解码测试,重复100次实验。解码过程的实验结果如表5所示。 Table 5 Experimental resultsof MRC algorithm decoding 表5 MRC算法方案解码实验结果 由表5可知,利用MRC解码算法求出的小喷泉码数据数目不固定,从表5的第2列可以看出,在3组样本的实验中,用于小喷泉码解码的数据量均大于192;由于随机种子长度缩短,所以试探解码小喷泉码的次数也比丢删编码方案的有所减少;大喷泉码的解码结果均为成功。 在上述2种方案的实验中,由于小喷泉码数据编码时被固定划分为192个分组,因此用于解码小喷泉码的数据分组数要大于或等于门限值才有可能成功解码。若用于解码的数据分组数量小于192,则模型不会进行小喷泉码解码而是直接返回解码失败。同理,当小喷泉码成功解码出参数K后,若用于解码大喷泉码的数据量小于K,也会直接返回解码失败,并返回失败原因。 5.2.1 解码成功率分析 对大小喷泉码模型与传统LT码进行解码成功率对比测试。源文件的原始分组数目K会影响相同冗余度下的解码结果,K越小越需要更高的冗余才能有较高的解码成功率。以丢删编码为例,对3幅图像数据分别进行冗余度1~1.2的解码实验,对每幅图像数据样本的各个冗余度分别进行100次重复实验。2种方法的平均解码成功率对比如图8所示。 Figure 8 Comparison of decoding success rate between two methods图8 2种方法的解码成功率对比 从图8可以看出,图像的上半部分,当用于解码的DNA序列冗余度达到1.04及以上时,大小喷泉码模型都能以接近100%的概率成功解码;图像的下半部分,传统LT码在冗余度为1.10的情况下,解码成功率约等于20%。传统LT码解码只使用BP算法,难以在较低冗余的情况下达到较高的解码成功率。 5.2.2 解码时间效率分析 本文使用大小喷泉码与传统喷泉码对大小为100 KB的图像进行解码时间的对比仿真实验。实验环境为:操作系统为Windows10 64位,处理器为Intel®CoreTMi5-7200U CPU @ 3.10 GHz,4 GB RAM。每组实验100次,结果取平均值,最终结果如图9所示。 Figure 9 Comparison of average decoding time between big and small fountaincode and traditional LT code图9 大小喷泉码与传统LT码平均解码时间对比 从图9可以看出,在相同的硬件环境下大小喷泉码模型的解码时间仅略高于传统喷泉码的,平均解码时间相差不超过10%。大小喷泉码模型解码时通过试探的方式确定随机种子长度,因此可能首先会进行多次小喷泉码解码,此过程需要花费一定的时间。此外大小喷泉码模型在解码后期对因缺少1度而无法继续解码的数据使用了ML算法继续解码。ML算法本质是高斯消元法求解方程组,可有效提高解码的成功率,但需要消耗更多的时间。设因缺少1度而无法继续解码的数据规模为S,则BPML算法解码的时间复杂度约为O((K-S)ln(K-S))+O(S3)。当解码的数据量达到一定冗余时,S的规模会很小,因此整个解码算法的复杂度仅略高于BP算法的。 5.2.3 数据存储密度分析 在数据存储密度方面,由于MRC算法编码的不均匀性,可能会导致编码生成的DNA序列超过规定长度。对该方案的数据分组长度进行适当压缩,让更多MRC编码生成的DNA序列小于或等于规定的长度,但因此会降低存储密度。在相同的实验参数下,3种方案的存储密度对比如图10所示(图10中纵坐标存储空间利用率即为存储密度)。 Figure 10 Comparison of storage space utilization among three schemes图10 3种方案的存储空间利用率对比 从图10可以看出,丢删编码方案具有更高的存储密度。丢删编码方案中每条编码的DNA序列中大喷泉码的存储密度比MRC算法方案的要多出约1.3%;而这2种方案与传统的LT码在数据分组末尾直接拼接整个参数L的做法相比,存储密度要高出约11.8%。 实验结果表明,本文提出的大小喷泉码模型能有效降低关键参数K传输的带宽,实现了以较低的带宽消耗传输一个关键参数的目的。 本文针对DNA存储应用场景下喷泉码中关键参数K的传递问题,设计了一种大小喷泉码模型。该模型中的小喷泉码作为带外信道负责向解码端传递一些大喷泉码解码过程需要的关键参数,并且在每个编码数据分组中,小喷泉码数据降低到了1 bit,有效压缩了关键参数传输的带宽,提高了空间利用率。 在未来的工作中,大小喷泉码模型需要进一步优化的方向是如何有效传递随机种子比特数信息。目前模型中随机种子是根据实际计算的长度动态嵌入到数据分组中的,而解码时,解码端无法获得随机种子比特数信息,只能通过试探的方法,借助小喷泉码的哈希自校验来确定种子比特数。这种方法的缺点是需要进行多次试探,会降低时间效率,未来可以进一步优化以提高时间效率。3.3 大小喷泉码模型结构
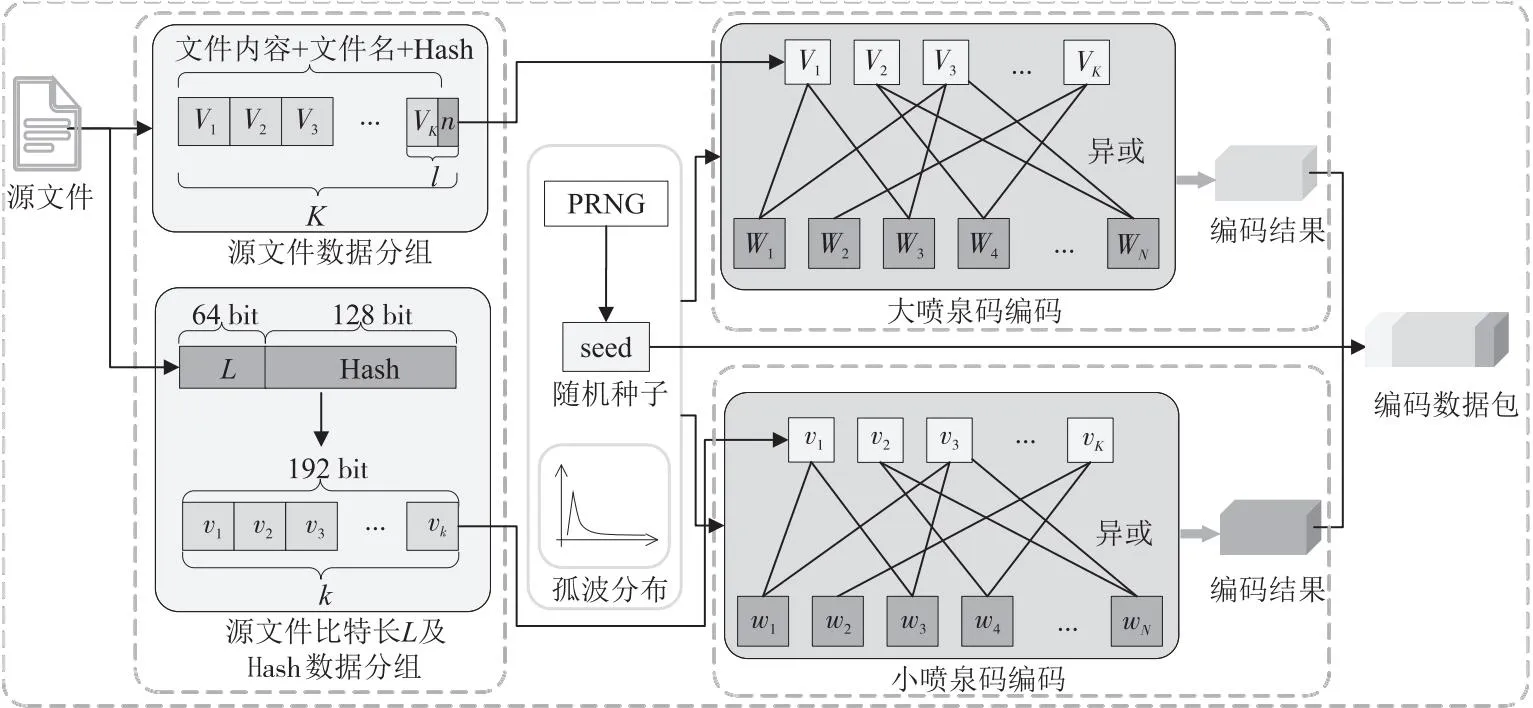
4 大小喷泉码编解码
4.1 DNA规避序列限制问题

4.2 大小喷泉码模型编码


4.3 大小喷泉码模型解码

5 仿真实验与分析

5.1 仿真实验测试


5.2 性能分析
6 结束语
