基于源文件可疑度的软件缺陷定位方法研究

陆皖麟，王 枭，冯 超，武 剑

(1.中国人民解放军66133部队， 北京 100043； 2.中国人民解放军66135部队， 北京 100043)

软件是由不同功能模块组成的系统集合，其中包含了大量源文件。当源文件中包含缺陷时，软件系统的部分功能将会发生损坏或导致整个软件系统瘫痪[1]。为对软件质量加以保证，规避其中潜藏风险，缺陷定位成为必不可少的关键步骤[2]。

本文将缺陷定位理论和缺陷预测方法相结合，提出了新的可疑度概念及其计算方法，将缺陷定位到源文件。主要从关联层—源文件和待定位缺陷的相关性，预测层—源文件的易错程度两个层次对每个源文件进行度量，度量结果定义为源文件的可疑度，可疑度越高，作为缺陷修复对象的可能性越大。

1 源文件可疑度定位方法框架

通过软件缺陷数据分析和缺陷定位相关理论[3]，构建出基于源文件可疑度的缺陷定位方法框架，如图1所示。其主要过程分为两个层，关联层首先依据缺陷数据的不同特征属性分析待定位缺陷和历史缺陷之间的相似关系，引入历史缺陷数据的修复信息对待定位缺陷数据和源文件进行相关性分析，并用相关度来度量源文件和待定位缺陷的相关性大小。预测层分析源文件的内在属性，例如代码规模，函数圈复杂度，环路复杂度，文件修改次数等[4]，源代码的不同度量元数据隐含着一定规律的缺陷信息，利用度量元数据构建的预测模型可以预测源文件包含相关缺陷的倾向性，即源文件的易错程度。

图1 基于源文件可疑度定位的方法流程

通过相关度和易错程度获得源文件的可疑度，定义可疑度计算公式表示为

Score=(1-a)Score1+aScore2

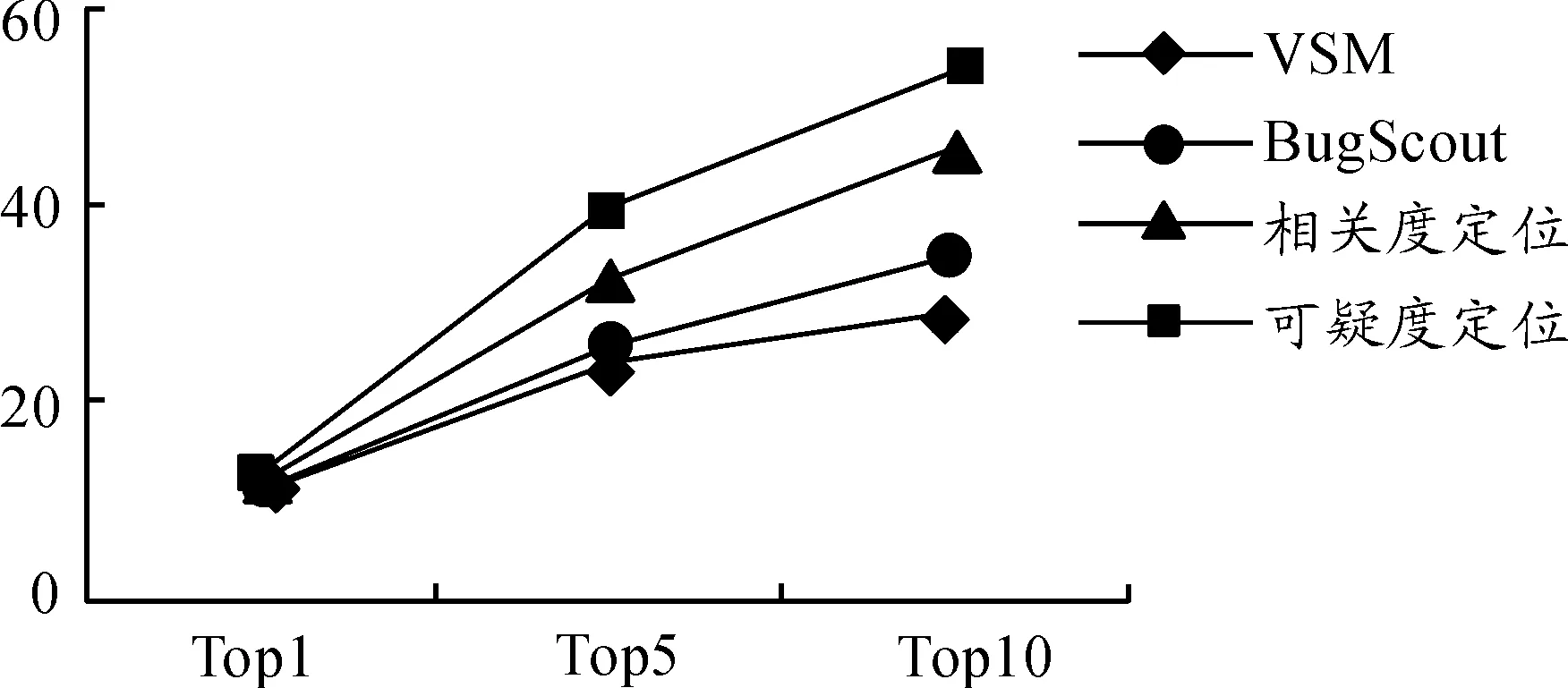
其中:Score1表示源文件和待定位缺陷的相关度，Score2表示源文件的易错程度，参数a用来调整相关度和易错程度在可疑度定位过程中的权重，0

2 关联层分析

关联层分析的目的是标记与待定位缺陷相关的源文件，并分析待定位缺陷和源文件之间的相关度[5]。主要分为3步：缺陷数据的相似度分析、历史缺陷和源文件的关联分析、待定位缺陷与源文件的相关度分析，过程如图2所示。

图2 关联层分析过程

2.1 缺陷数据的相似度分析

根据软件缺陷数据的特点，首先从缺陷记录信息中提取能够表征缺陷数据的特征属性，依据向量空间模型思想将缺陷特征属性抽象化处理，并建立缺陷数据的数学矩阵模型；其次，结合样本之间的相似系数和距离系数构建改进后的模糊相似矩阵，通过传递闭包运算得到模糊等价矩阵；最后利用模糊等价矩阵获取待定位缺陷数据和历史修复缺陷的相似度。该方法能够同时对大规模的缺陷数据进行处理，主要分为5个步骤：

1) 特征属性提取及抽象化编码。通过对软件缺陷数据的分析，共提取10种特征属性用于缺陷之间的相似度分析[6]，具体内容如表1所示。

表1 软件缺陷数据的特征属性

抽象化编码具体规范：如果属性f取离散化的数值，且0<|f|<∞，则把属性取值编码为“1”，“2”，…；如果属性f取连续的数值，且0<|f|<∞，则把属性取值编码为“1”，“2”，…；如果属性f值缺失(即缺陷i或j缺少属性f的度量值)，则xif=xjf=0。根据上述抽象化编码规范，得其编码方式如表2所示。

表2 缺陷数据的抽象编码

当存在n个缺陷数据时，全部进行抽象化编码后可映射为n个缺陷特征向量，进一步表示为一个多维矩阵模型，矩阵的每个行向量表示一个缺陷数据，每个列向量表示缺陷数据的一个特征属性，元素xij表示第i个缺陷数据的第j个特征属性的编码值，其数学形式表示为

(1)

2) 数据规范化处理。缺陷数据的相似度分析过程中，缺陷集合X={x1,x2,…,xn}表示的是包含10个特征属性的所有n个缺陷对象。为了消除缺陷属性编码值数量级或单位的差别，需要对抽象化的缺陷数据进行规范处理，将每一特征属性的编码值规范到[0,1]，消除不同量纲带来的影响，进一步提升缺陷数据相似度分析方法的效果。笔者采用平移极差变换的方法将缺陷数据规范化处理，如式(2)：

(2)

3) 模糊相似矩阵的构建。对于缺陷数据的非空集合X(x1,x2…,xn)，为计算集合X中缺陷xi和缺陷xj之间的模糊相似关系,定义X和X之间的模糊关系R满足R∈f(X×X)，为X和X的直积，即X×X={(xi,xj)|xi∈X,xj∈X}。其中，R(xi,xj)表示元素xi和元素xj之间的相似度，且满足R(xi,xj)→[0,1]。则集合X中缺陷之间的模糊关系可表示为m×n的模糊相似矩阵：

(3)

简记为R=(rij)n×n，矩阵中rij=R(xi,xj)表示X中缺陷i和缺陷j之间的相似关系。

通过规范化后的缺陷数据建立上述模糊相似矩阵，考虑10种缺陷数据特征属性对距离贴近程度和相关关系程度的影响不同，采用距离系数描述缺陷属性之间的距离贴近程度，相似系数描述缺陷属性之间的相关关系程度。因此将相关系数和距离系数结合共同构建缺陷数据之间的模糊相似矩阵R= (rij)n×n，进一步提高相似度分析结果的准确性。

相似系数的计算公式为

(4)

距离系数计算公式为

(5)

最终相似度计算公式为

rij=δ1sij+δ2dij

(6)

其中，i,j=0,…,n，sij和dij分别表示缺陷数据xi和xj的相似系数和距离系数，δ1，δ2表示相似系数和距离系数各占比重，其中δ1+δ2=1，笔者将相似系数和距离系数赋予相同的比重，即δ1=δ2=0.5，由此可以构造出模糊相似矩阵R= (rij)n×n。

如果模糊相似矩阵R= (rij)n×n满足自反性、对称性、传递性，则rij能够准确表示缺陷i和缺陷j之间的相似度，通过模糊相似矩阵R= (rij)n×n的构建方法分析，其满足自反性和对称性，但是不满足传递性，所以需进行下一步模糊等价矩阵的构建。

4) 模糊等价矩阵的构建。为了使rij能够如实反映缺陷i和缺陷j之间的相似关系，需要对模糊相似矩阵进行改造，即构建模糊等价矩阵T。笔者采用求传递闭包t(R)的经典算法—平方法计算模糊等价矩阵。

平方法的主要过程是将模糊相似矩阵R不断自乘[7]，当自乘过程首次出现Rk·Rk=Rk时，所得到的传递闭包Rk即为模糊等价矩阵T。因为模糊等价矩阵满足自反性，对称性和传递性，所以模糊等价矩阵T中的元素tij能够准确表示缺陷i和缺陷j之间的相似度，根据模糊等价矩阵T中能够得到任一缺陷和其他缺陷的相似度。

5) 截矩阵的构建。给定任意α∈[0,1]的阈值，对于X和X之间的模糊关系T，截集Tα表示为Tα={(xi,xj)∈X×X|tij≥α}。对于二元组(xi,xj)∈Tα，表示缺陷xi和缺陷xj满足阈值α水平的相似关系。

定义：设给定模糊等价矩阵T=(tij)n×n，对任意α∈[0,1]，记

Tα=(αtij)n×n

(7)

其中：

(8)

则称Tα=(αtij)n×n为T的α截矩阵。

模糊等价矩阵的α截矩阵是一个布尔矩阵，通过缺陷数据集合建立模糊等价矩阵T之后，就能够依据截矩阵将某行或某列为1的对象划归到一类。

假设，缺陷数据1，2，3之间的模糊等价矩阵为

设置阈值α=0.5，则T的α截矩阵为

为确定与缺陷2相似的缺陷，只需提取Tα中的第2行或第2列中为1的元素，其中，t23或t32为1表示与缺陷2和缺陷3满足阈值水平的相似关系。

设置不同的α阈值，缺陷之间的相似关系提取结果也不同。在α从0～1的变化过程中，模糊等价矩阵T的α截矩阵也会随之改变，α越大提取的缺陷之间的相似度也越高。

2.2 历史缺陷和源文件的关联

历史缺陷信息不仅包含缺陷的各种特征属性，还包括缺陷修复的源文件位置信息等，根据其修复信息可以追溯每个缺陷所变更的程序源文件，历史修复缺陷和源文件的相关性分析就是建立历史缺陷及其修复的源文件的链接关系。

定义(缺陷修复位置关系图)：把缺陷和源文件抽象化在图中用各个节点表示，位置关系G=(S，F)表示缺陷和源文件的位置关系，其中S代表所有缺陷数据，F代表程序源文件。如图3所示，缺陷s1所修改的源文件为f2，缺陷s2所修改的源文件为f4，连接线表示缺陷和源文件之间的链接关系。

图3 缺陷修复位置关系

2.3 待定位缺陷和源文件的相关度分析

当一个待定位缺陷B提交时，首先需要对其相似的历史修复缺陷和历史缺陷所变更的源文件进行分析，然后构造一个3层异构图，如图4所示。第1层的节点表示待定位缺陷B；第2层表示历史修复缺陷中与待定位缺陷B相似的历史修复的缺陷数据集S，其相似程度依据阈值大小进行设置；第3层表示历史修复缺陷所变更的程序源文件集合F，通过对历史缺陷数据的修复信息进行查询，建立历史修复缺陷数据和源文件的链接关系，表示这些源文件对第2层的历史缺陷数据产生影响。

图4 待定位B缺陷和源文件的关联关系

因此，待定位缺陷和程序源文件的相关度分析过程中，首先需要对待定位缺陷和历史修复缺陷进行相似度分析，建立第1层和第2层的关联；然后根据历史修复缺陷所变更的源文件信息建立第2层和第3层的关联；最后得到第1层待定位缺陷和第3层程序源文件的相关度。其中，待定位缺陷和程序源文件的相关度Score1的计算公式如下：

其中，Similarity(B,Si)表示待定位缺陷B和历史修复缺陷Si的相似度；m表示所有与程序源文件Fi相关联的缺陷Si的数量；n表示Si相关的源文件个数。

3 预测层分析

预测层分析是通过缺陷预测方法对关联层标记的源文件进行易错程度分析的过程。将缺陷密度[8]作为源文件易错程度的度量，首先选取对缺陷密度影响较大的度量元构建源文件缺陷密度预测模型，然后对源文件的缺陷密度进行预测，获得源文件易错程度的度量。主要思路是将源文件的度量元作为预测过程的输入，将源文件的缺陷密度作为预测过程的输出，通过相应的预测方法建立度量元和缺陷密度之间的关系，用于下一步的预测，如图5所示。

图5 缺陷定位的预测层分析框架

3.1 源文件度量元的选择

为保证源文件缺陷密度预测的准确性，需对缺陷密度和度量元进行相关性分析，选择对缺陷密度影响较大的度量元作为预测模型的输入。采用Spearman秩相关系数的分析方法，用来计算度量元和缺陷密度之间的相关系数。

给定度量元和缺陷密度的n组源文件数据，可表示为X(x1,x2,…,xn)和Y(y1,y2,…,yn)。其中，xi表示第i个源文件的度量元的值，yi表示第i个源文件的缺陷密度。首先将和中数据进行组对，即(x1,y1),(x2,y2),…,(xn,yn)。然后将xi和yi分别按照数值大小进行排列，获得和各自所占名次(即秩)，记作Ri和Si。由此可以得到数据组(x1,y1)，(x2,y2)，…，(xn,yn)的n对秩，即(R1,S1),(R2,S2),…,(Rn,Sn)。利用Spearman等级相关系数衡量度量元X和缺陷密度Y之间的相关程度，可表示为

(9)

标准的相关系数和相关关系的评价指标如表3所示，选取满足相关系数阈值的源文件度量元，构建源文件的缺陷密度预测模型。

3.2 预测模型构建

支持向量机(Support Vector Machine，SVM)在小样本、非线性和高维度空间的模式识别中具有独特优势[9-10]，通过支持向量回归(Support Vector Regression，SVR)构建源文件缺陷密度预测模型。

表3 相关关系评价指标

源文件缺陷密度预测就是给定数据样本集合{(x1,y1),…,(xi,yi),…,(xl,yl)}，其中，xi表示源文件的度量元向量，yi表示源文件缺陷密度，xi∈Rn,yi∈R，i=1，2，…，l。在Rn上寻找f(x)=w·x+b来拟合，使集合点与超平面的误差较小，定义正则化的误差函数:

假设允许模型的预测值与真实值有一定的偏差ε，则在模型中定义一个损失函数，用于调和预测值和实际值的误差，这种类型的函数就是ε不敏感损失函数。

ε不敏感损失函数定义为

Lε=|yi-f(xi)|ε=max{0,|yi-f(xi)|-ε}

利用定义的ε不敏感损失函数忽略一定范围内的误差，当样本点位于两条虚线内的管道时，认为该点没有损失，两条虚线构成的管道为ε-管道。处于虚线上的样本决定了ε-管道的位置，这部分样本称为“支持向量”，如图6所示。

图6 非线性回归函数的不敏感带

回归问题则等价于最优化问题：

在上述模型中，需要事先确定损失函数中的参数ε，笔者基于上述原理构建出ν-SVR的缺陷密度预测模型，将ε的值自动最小化，并使用非负常数ν控制支持向量的数目。另外选择合适的核函数K(xi,xj)，把上述回归问题转化为最优化问题：

(10)

对偶问题为

(11)

其中，ν和C为常数。最终建立的SVR预测模型为

(12)

4 实验及分析

4.1 实验设计

为了体现本文缺陷定位方法的通用性，选用Eclipse平台的开源项目AspectJ中的缺陷数据。该项目中有完整的缺陷数据库和历史变更记录，并具有不同数量的缺陷和源代码文件。将AspectJ项目中的缺陷数据作为历史缺陷，并从中选取2002年7月至2006年10月的286个缺陷数据作为待定位缺陷，其中的源文件共有6 485个。

实验提取286个缺陷数据，将每个缺陷数据进行抽象化编码。通过关联分析和预测分析，获取每个缺陷数据所对应的源文件可疑度排序，完成每个缺陷的定位工作。最后通过分析验证上述缺陷数据实际所修复的源文件位置，对定位结果的准确性进行评估。

4.2 结果分析

为评估本文缺陷定位方法的效果，依据现阶段普遍采用的TopN(TopN Rank)、MRR(Measurement Result Recording) 、MAP(Mean Average Precision)3项评估指标对该方法的实验结果进行对比。实验对比4种缺陷定位方法，方法1采用VSM定位方法[11]；方法2采用BugScout定位方法[12]；方法3为本文缺陷定位方法中仅采用待定位缺陷和源文件的相关度(a=0)，相似度阈值为0.55时的定位结果。方法4为本文基于源文件可疑度(a=0.2)，核函数为径向基函数(RBF)的定位结果，上述4种方法的定位结果如表4所示。

表4 不同方法的缺陷定位结果

本文针对TOP1，TOP5，TOP10的准确率对上述4种方法进行对比分析，对比结果如图7所示。

图7 开源项目AspectJ中不同缺陷定位方法结果

通过图7对比结果可知，基于可疑度的缺陷定位方法总体效果较好。TOPN表示可疑度排序的前N个源文件中包含需要修复的源文件的准确率，从TOP1的角度分析，四种方法的定位效果基本相似，因为定位问题本身的复杂性，相对来说TOP1的准确性仍处在较低的水平，本文定位方法的优势并未得到突显。从TOP5和TOP10的角度分析，方法4相比于方法1和方法2具有较为明显的优势，其中方法1和方法2的定位过程是从信息检索的角度出发，检索缺陷报告和源文件中代码的文本相似度，但是一般情况下缺陷报告采用自然语言描述，源文件采用程序语言描述，因为源文件和缺陷报告的语言空间不同，所以对定位效果有一定影响，容易产生不理想的结果。

方法3所得的源文件可疑度排序列表，虽然能够定位到程序源文件，但是忽略了缺陷修复的行为规律和源代码自身代码质量。方法4既考虑了源文件和待定位缺陷之间的相关度，又考虑了源文件的内在结构和历史修复信息即对源文件易错程度的预测。上述实验表明：采用本文方法对缺陷进行定位能够取得较好的效果。