新型MEMS电容薄膜真空计设计与仿真数据分析

黄麒麟,许马会,单文桃,冯勇建

(1.江苏理工学院机械工程学院,江苏常州 213001;2.厦门大学航空航天学院,福建厦门 316005)

0 引言

随着航天航空技术的发展,对真空压力传感器的要求越来越高,而电容薄膜真空计具有准确度高,稳定性良好的特点,并且测量结果不会被其他气体干扰,在真空环境下实用性很高。为了研究MEMS电容薄膜真空计的测量范围,提高输出线性度与抗过载能力,很多学者对感压薄膜结构进行了优化设计。传统电容薄膜真空计不仅质量大,而且体积也相对较大,使用范围受到极大限制,难以满足一些特殊领域的应用需求,尤其是航天领域对测量精度与环境有严格要求。MEMS技术的出现,电容薄膜真空计的研究向质量轻、高精度、微型化等方面发展。

F.Fabbri等[1]利用镍微梁的转移特性研制一款压力传感器,该传感器主要针对较大压力进行测量,尤其在10～1 000 Pa范围内对压力测量的灵敏度高,具有良好的可靠性与稳定性,若测量压力超过上限或低于下限时,会出现较大测量误差。S.Y.Woo等[2]提出了一种新型电容式膜片计的校正装置,对补偿电路进行优化与完善,在增大量程的同时减小了误差,能够在10～13 000 Pa范围进行压力测量,但是在测量微弱压力时,测量结果误差大。J.C.Brian等[3]提出了一种基于MEMS系统的带有双散热器的皮拉尼计,利用重掺硼(p++)硅作为其结构材料。该结构可以集成各种用MEMS技术制造的传感器,可以用于现场真空测试。该结构可以用来测量2.6～266 Pa范围的压力,且具有更高灵敏度与线性度,可以与真空包装内MEMS设备集成,监测包装内的长期压力变化和稳定性。

国内许多机构已经对薄膜真空计的测量展开了一系列的研究。王呈祥等[4]对MEMS型电容薄膜真空计开展了初步测试,提高输出线性度与抗过载能力,对感压薄膜结构进行了优化设计,如把感压薄膜由平膜结构设计成中心岛结构[5]、环形岛结构[6]或波纹状结构[7],测量下限可以达到5 Pa。王凡等[8]研制了一种能够满足空间探测工程需要的真空压力传感器,采用自适应非线性补偿电路、温度补偿电路等,解决传感器输出信号非线性的补偿问题;采用电容式薄膜封装结构,壳体为电容的另一极,在0.1～100 Pa的测量范围内实现了传感器0.2%FS的测量精度。

1 薄膜真空计结构与工作原理

薄膜真空计采用硅材料制造,主要结构由硅岛、简支梁、感压薄膜组成,如图1所示,图中所示腔体为参考腔,在薄膜结构上载有感应电容变化的梁结构。其中每个梁结构的硅岛与下层薄膜相连接,一侧硅岛固定在硅基底区域,另一侧固定在薄膜结构上。基于MEMS技术的新型电容薄膜真空计,其薄膜的表面有一层压力感应膜,在压感薄膜受到外界压力的同时,其轴向挠度发生变化,使硅岛发生横向的位移,此时每组与硅岛相连的梁,因受到外力而发生形变被拉伸,从而导致每组梁之间设置的平板电容发生改变。通过ANSYS软件进行建模,输入结构参数仿真得出云图,根据结果优化该薄膜真空计的结构。通过测量梁结构上的电容梳齿微小距离变化,感测所产生的真空度的变化,实现0.001～1 Pa范围的真空度测量,实现大电容变化量的检测。

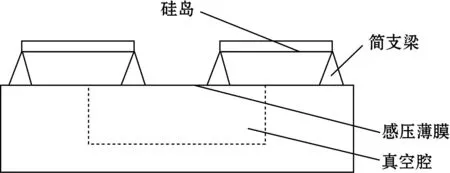
(b)侧视图图1 薄膜真空计结构图

本文采用感压薄膜与简支梁组合,设计了一款新型的正方形简支梁梳齿结构,正方形薄膜结构是一种常用的感压薄膜结构,因为正方形具有良好的几何优势,能够快速确定参数的输入输出关系。在MEMS电容薄膜真空计中,感压薄膜四边固定于硅基底上,当受到压力作用时,感压薄膜会发生形变。矩形薄膜坐标图如图2所示。

图2 薄膜坐标图

矩形薄膜的挠度变化公式：

(1)

式中：ω为感压薄膜上坐标位置挠度;ω0为感压薄膜中心位置挠度;a为正方形薄膜1/2边长。

(2)

(3)

式中：p为薄膜所受压强;D为弯曲刚度;E为材料弹性模量;ν为泊松系数;h为感压薄膜厚度。

式(1)中,因为硅岛在y轴方向的角度变化相对较小,可使y趋于0,得出式(4)：

(4)

对此式进行求导后得：

一阶导数为

(5)

二阶导数为

(6)

其中变面积部分的电容变化量可以表示为

(7)

变极板距离部分的电容变化量可以表示为

(8)

总电容变化量表示为

(9)

式中：ε为真空中介电常数;d为梳齿与固定电极的间距;h为梁的厚度;n为梳齿数量;Δx为简支梁传递给梳齿的位移量。

梳齿结构示意图如图3所示。

图3 梳齿结构示意图

薄膜真空计在非工作状态,薄膜保持水平状态;当受到外界环境施加的压力时,薄膜结构向下发生形变。然后薄膜上的硅岛结构会因薄膜形变产生弯曲角度;由于硅岛与简支梁相连接,简支梁结构随之发生拉伸,此时位于简支梁中心感应电容的梳齿结构间距离会增大,其变化量为Δx。由于Δx的产生,梳齿电容会产生变化,通过检测该电容变化,可以间接检测到环境压力的变化。

2 薄膜真空计结构参数与仿真

MEMS薄膜真空计各项参数见表1所示。

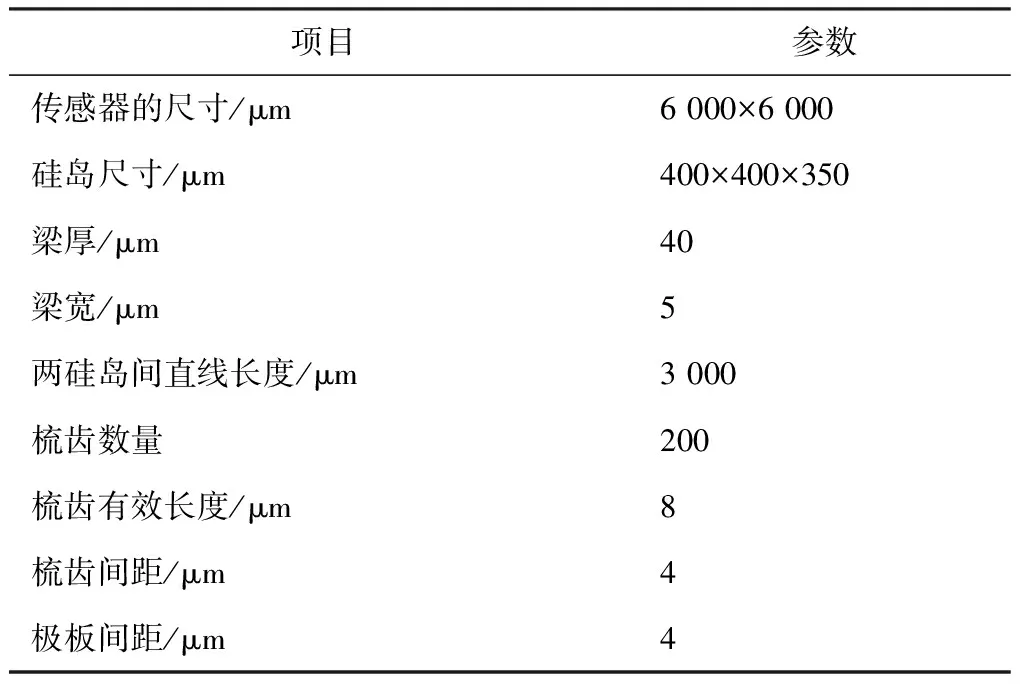
表1 真空计模型参数表

将表1参数导入ANSYS中进行仿真后,感压薄膜变形云图和简支梁变形云图如图4所示。在施加0.001 Pa压力时,将几何模型重新导入ANSYS中,进行求解。

图4 感压薄膜形变云图与简支梁形变云图

图5 MEMS薄膜真空计模型图

图6 硅岛x轴位移云图

MEMS薄膜真空计模型如图5所示。对结构进行有限元仿真,得硅岛在x轴位移云图,如图6所示。当结构受到外界压力的挤压时,膜结构发生形变,薄膜结构上的硅岛会产生一定的位移量与转角,直接影响简支梁结构的位移量。

硅岛根部至硅岛顶端的x轴位移图如图7所示。从图7可知,硅岛的位移随高度增加呈线性变化。硅岛随薄膜产生位移时,位移在硅岛根部最小,沿着硅岛向硅岛顶端逐渐增大,在硅岛顶端获得最大位移。分析位移分布图的目的是找出硅岛最大位移量产生的位置,使梁结构产生最大形变,从而布置最佳的硅岛位置。

图7 硅岛根部至硅岛顶端的x轴位移图

3 分析

3.1 电容极板的位移分析

改变硅岛结构x轴坐标,可得图8坐标系。从图8(a)可得,z轴方向均布载荷时,硅岛中心位置距yoz平面1 800 μm处,硅岛顶端产生的最大位移为0.075 nm。

从图8(b)可得,z轴方向均布载荷时,硅岛中心位置距xoz平面230 μm处,电容极板的最大位移为0.297 nm。

(a)硅岛顶端位移

(b)电容极板位移图8 硅岛位移坐标图与电容极板位移坐标图

从上述结论中可以得出,当薄膜上的硅岛距离中心平面的距离在1 800 μm左右时,硅岛顶端能够获得最大位移;且硅岛距离中心的平面距离为230 μm时,电容板能获得最大位移。所以,此处为薄膜的敏感区域,硅岛布置在此处薄膜真空计能获得最大灵敏度。

3.2 薄膜真空计灵敏度分析

通过仿真,得压力与梳齿电容极板位移之间的压力-位移坐标图,如图9所示。从图9(a)可得,在0.1～1 Pa之间,压力不断增大时,平板位移也不断增大,压力到达测量上限时,平板位移为450 nm。从图9(b)可得,在0.02～0.1 Pa之间,对压力变化的感应更灵敏,平板位移变化与压力变化成正比例函数关系。

(a)0.1～1 Pa压力范围

(b)0.02～0.1 Pa压力范围图9 压力-位移坐标图

通过仿真模型结果和式(8),得出压力-电容的数值关系坐标图,如图10所示,分析0.001～1 Pa时薄膜真空计的灵敏度。从图10(a)可得,当压力在0.001～0.1 Pa之间,压力只有微小的变化量,电容随之也产生对应的变化,电容值下降趋势缓慢;从图10(b)可知,当压力在0.1～1 Pa之间,随着压力增加,电容变化幅度增大,电容对压力变化的检测灵敏度增加,此时电容值出现坍塌式下降。

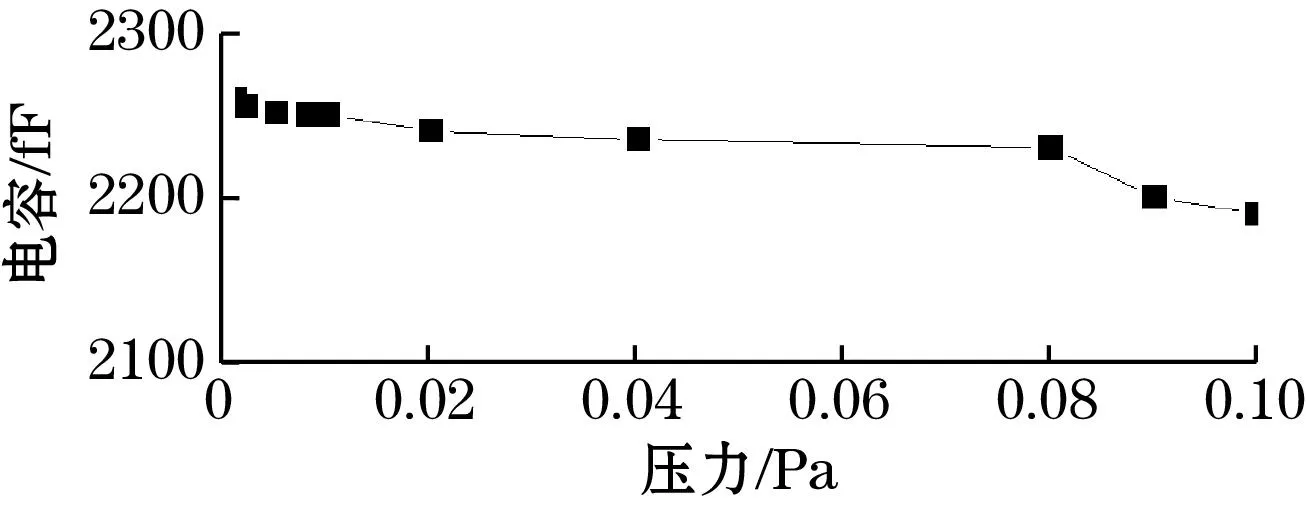
(a)0.001～0.1 Pa压力范围

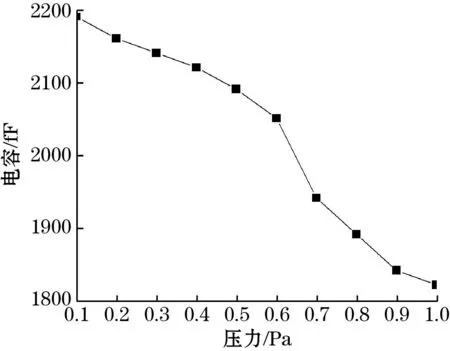
(b)0.1～1.0 Pa压力范围图10 压力-电容坐标图

3.3 传感器灵敏度的误差分析

结构设计过程中,传感器的压感薄膜厚度与尺寸会影响传感器的灵敏度;简支梁结构的直线长度对传感器灵敏度有影响。

分析不同厚度压感薄膜对薄膜真空计的影响,压力为1 Pa时,对不同膜厚的薄膜真空计进行仿真,得到薄膜厚度与电容变化量之间的关系,灵敏度变化趋势如图11所示。由图11可知,当压力恒定时,电容变化量会随着压感薄膜的厚度增大而逐渐变小。

图11 薄膜真空计的灵敏度随压感薄膜厚度变化趋势

分析不同梁结构的直线长度对薄膜真空计的影响,压力为1 Pa时,对不同梁结构长度的薄膜真空计进行仿真,得到灵敏度变化趋势如图12所示。由图12可知：当压力恒定时,当简支梁在3 000 μm以内,电容变化量增幅明显;不同膜厚条件下,当简支梁长度超过3 000 μm之后,已经超过其有效长度,增幅开始逐渐变缓,电容变化量会逐渐趋于恒定值,电容量到达饱和状态。

图12 薄膜真空计的灵敏度随简支梁长度变化趋势

4 结论

本文设计了一种基于MEMS技术的复合结构硅基薄膜真空计。设计采用薄膜与简支梁复合结构,在0.001～1 Pa压力范围内有良好的测量效果。为了提高该结构的测量性能,通过ANSYS建立了薄膜真空计有限元模型,对所得数据进行受力状态仿真分析,并对梁结构与薄膜结构之间的尺寸进行优化。分析结果表明,设计的硅基新型薄膜真空计可以准确测量0.001～1 Pa范围的压力。