基于DBO-PSO-BPNN的Stewart平台正运动学求解方法研究

乔贵方,聂新港,付冬梅,张 颖,姚逸秋

(南京工程学院自动化学院,江苏南京 211167)

0 引言

近些年,多自由度并联机器人在智能制造领域中的应用越来越广泛。并联机器人通过调节6个支杆长度实现位姿控制[1],支杆长度与机器人位姿之间的映射关系具有强耦合非线性。其正运动学解算需要求解1组含有6个未知数的非线性方程组[2],无法得到正运动学的解析解。

目前,并联机器人的正运动学解算有多种计算方法,B.N.R.Abadi等提出了实时求解并联机构运动学问题的多种解决方案[3]。M.Liu等提出一种多元多项式回归运动学正解算法,将多元多项式回归与牛顿迭代法相合,得到一种精度可控的高效求解算法[4]。谢志江等提出了基于最速下降法和多元牛顿法的组合数值优化方法,提高了优化算法的迭代收敛速度[5],然而基于传统数值优化算法求解精度依赖于初值的选取。为了降低对初值的依赖程度,较多的学者利用智能算法解决并联机器人的正运动学问题[6]。李平等提出一种混合人工蜂群和牛顿迭代混合算法,实现了4-SPS-CU、3-RRR 2种机器人的正运动学求解[7]。L.Li等采用粒子群算法对BP神经网络进行训练,实现了较好的求解精度[8]。D.Guo等提出了一种基于神经网络的五自由度并联平台控制方法[9]。H.Q.Zhang等提出一种基于BP神经网络的Newton Raphson混合算法用于模拟平台的轨迹移动,为并联机器人的控制奠定了基础[10]。然而六自由度并联机器人的末端位姿包含位置和姿态,但位置和姿态数据的量纲不同,并且位置和姿态误差在数值上也相差1～2个数量级,因此,通过传统的BP神经网络进行数据拟合会导致其拟合效果较差。

本文针对Stewart并联机器人的正运动学求解问题开展研究,提出了一种基于DBO-PSO混合优化算的双级BPNN正运动学智能解算方法,通过仿真实验验证了该方法具有较好的正运动学求解精度。

1 Stewart并联机器人运动学模型

本文研究的Stewart并联机器人如图1所示,针对该机器人建立其运动学模型[11]。Stewart并联机器人的上、下平台通过电缸、卧式虎克铰连接在一起。上平台卧式虎克铰的铰接点构成的平面定义为上铰接点平面A,该平面的铰接点坐标定义为Ai,i=1,2,…,6;下平台卧式虎克铰的铰接点构成的平面定义为下铰接点平面B,该平面的铰接点坐标定义为Bi,i=1,2,…,6;上铰接点平面A的中心点建立动坐标系O1-X1Y1Z1,下铰接点平面B的中心点建立静坐标系O-XYZ,动坐标系O1-X1Y1Z1在静坐标系O-XYZ中的位姿表达为(x、y、z、α、β、γ),对应的位姿变换矩阵T如式(1)所示：

(1)

根据Stewart并联机器人的空间向量闭环关系可以得到式(2)：

li=P+RBi-Ai

(2)

式中：li为电缸(支杆)在静坐标系O-XYZ下的向量;

P、R分别为动坐标系O1-X1Y1Z1在静坐标系O-XYZ下的位置向量和旋转矩阵。

图1 Stewart平台结构简图

2 基于DBO-PSO BPNN算法的正运动学解算

2.1 双级BPNN模型建立

图2 基于DBO-PSO优化的BPNN结构图

利用大量的数据对BPNN进行训练,可以得到输入与输出之间的非线性关系。训练过程中主要对权值和阈值进行调整,以训练数据的误差绝对值为目标,通过迭代学习,达到设定的迭代次数后停止学习。但是初始权值和初始阈值是随机产生的,由于初始权值和初始阈值直接影响BPNN的结果,因此,本文使用DBO-PSO优化算法对上文提出的BPNN进行初始权值和阈值的优化。

2.2 蜣螂优化算法模型

蜣螂优化算法是东华大学的沈波教授于2022年提出的一种群智能优化算法[12]。蜣螂优化算法分为滚球、繁殖、觅食和偷窃4个基本步骤,一个种群按照6∶6∶7∶11的比例,将蜣螂划分为不同的角色,如图3所示：

图3 蜣螂种群分布示意图

2.2.1 蜣螂滚球

2.2.1.1 无障碍物模式

当蜣螂前行无障碍时,蜣螂滚球行为会利用太阳进行导航,蜣螂位置更新公式如下：

(3)

2.2.1.2 有障碍物模式

当蜣螂遇到障碍物时,通过跳舞获得新的前进方向,使用切线模仿跳舞行为获得新的滚动方向,滚动方向角度为[0,π]。此时位置更新公式为

(4)

当θ=0、π/2或π时,tanθ为0或∞,蜣螂位置不会更新。

2.2.2 蜣螂繁殖

蜣螂会将粪球滚到适合产卵的安全地方,因此,提出一种边界选择策略来模拟蜣螂产卵的区域,公式如下：

(5)

当确定产卵区域后,每只雌性蜣螂在每次迭代中产生一个雏球,雏球的位置在迭代过程中是动态的,位置更新公式如下：

(6)

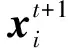
2.2.3 蜣螂觅食

一些成熟的小蜣螂会从地下出来觅食,小蜣螂的最佳觅食区域是动态更新的,公式如下：

(7)

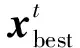
小蜣螂的位置更新如下所示：

(8)

式中：C1为正态分布的随机数,即C1∈N(0,1);C2为1×D的属于(0,1)之间的随机向量。

2.2.4 蜣螂偷窃

在种群中,会有一些蜣螂从其他蜣螂那里偷粪球,盗贼蜣螂的位置更新如下：

(9)

式中g为1×D的属于(0,1)之间的随机向量。

2.3 DBO-PSO混合优化算法

PSO优化算法通过群体中粒子个体之间的协作和信息共享寻找最优解,粒子个体通过跟踪个体极值和全局极值更新位置。粒子群算法的个体位置变化按2个基本公式：

(10)

为提高算法的全局优化能力,本文将DBO算法于PSO算法相融合,从而提高DBO算法的全局搜索能力。蜣螂滚球分为无障碍模式和有障碍模式。各种群位置更新公式如下：

无障碍模式种群位置更新公式为

(11)

式中c3、c4分别为DBO优化算法和PSO优化算法的比例系数。

有障碍模式种群位置更新公式为

(12)

蜣螂繁殖种群位置更新公式为

(13)

蜣螂觅食种群位置更新公式为

(14)

蜣螂偷窃种群位置更新公式为

(15)

3 实验仿真结果分析

用于本文的Stewart并联机器人三维结构图如4所示,其结构参数如表1所示,其中铰接点坐标均表示在静坐标系O-XYZ下。在Stewart并联机器人的运动空间范围内随机选取500组位姿,利用逆运动学求出每组位姿对应的支杆长度作为BPNN的训练集和测试集。随机选择350点构成训练集,150点作为测试集。

图4 Stewart平台结构图

表1 Stewart平台结构参数

本文提出的DBO-PSO优化算法中比例系数c3为0.1,比例系数c4为0.9,迭代次数为100。采用正运动学解算误差值作为模型迭代时的适应度值,DBO-PSO优化算法的适应度曲线如图5所示。从图5可以看出,适应度函数很快收敛到稳定值。

图5 最佳适应度曲线

为了验证DBO-PSO 双级BPNN优化算法正解的优越性,采用相同数据集,并将初始值优化迭代次数均设置为100,对比DBO、PSO算法优化后的平均综合位置、姿态误差进行对比,算法对比结果如图6、图7所示。

图6 Stewart并联机器人正运动学解算测试集的平均综合位置误差

图7 Stewart并联机器人正运动学解算测试集的平均综合

模型求解误差如表2所示,从表2中可以看到,与基于DBO双级 BPNN的求解结果相比,基于DBO-PSO 双级BPNN求解结果在平均综合位置、姿态误差分别降低了92.35%、90.76%,与基于PSO 双级BPNN的求解结果相比,基于DBO-PSO 双级BPNN求解结果在平均综合位置、姿态误差分别降低了34.16%、11.10%,与基于DBO-PSO 单级BPNN的求解结果相比,基于DBO-PSO 双级BPNN求解结果在平均综合位置/姿态误差分别降低了87.91%、85.39%。

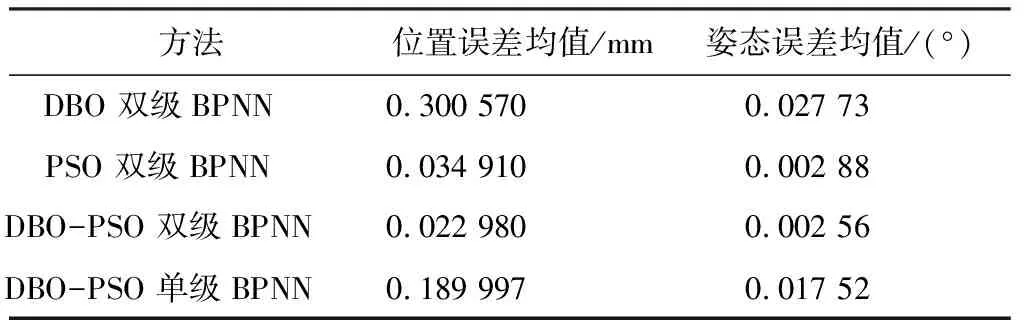
表2 模型求解误差

4 结论

本文首先对Stewart并联机器人进行运动学建模,并根据位姿数据的量纲不同,提出构建了一种双级BPNN;其次为实现正运动学的精确解算,提出一种DBO-PSO融合算法对双级BPNN的初始权值和阈值进行优化。最后为验证以上BPNN的结构和DBO-PSO融合算法的效果,在Stewart并联机器人运动空间随机选取了500组位姿,利用逆运动学求出每组位姿对应的支杆长度作为BPNN的训练集和测试集,将本文提出的DBO-PSO BPNN与DBO-BPNN、PSO-BPNN进行实验结果对比。从实验结果可以看出,本文提出的DBO-PSO BPNN在求解Stewart并联机器人正运动学的精度更高。