基于暂态电流的三相变压器剩磁测量系统

田思雨,汪友华,刘成成,武仕朴,任于展

(1.省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学),天津 300130;2.河北省电磁场与电器可靠性重点实验室(河北工业大学),天津 300130)

0 引言

变压器作为电力传输和分配系统的关键组成部分之一,其稳定的工作状态对电网的稳定性和可靠性至关重要。通常情况下,当变压器工作时,变压器内部的铁芯会因为电流的通过而磁化。当变压器断电时,由于变压器使用的铁磁性材料磁滞作用,会使铁芯中留有一定的磁通,这部分磁通就是剩磁,剩磁一旦产生,便不会轻易消失。这些剩余磁通会在后续的运行中对变压器产生不良影响,可能导致饱和、过热、损坏等问题。因此,测量和消除变压器的剩磁显得尤为重要。

常见的测量剩磁方法有磁强计法、注磁电流法和磁滞回线法等。磁强计法使用霍尔效应磁强计测量剩磁,虽然测量简单高效,但无法测量剩磁的分布情况,也不适用于大尺寸结构变压器的剩磁测量[1];注磁电流法需要供给激励以改变剩磁电流,并测量感应电势信号以确定剩磁的大小,但该方法需要断开变压器的电源,对于不方便停运的的大型变压器等设备不太适用[2];磁滞回线法通过测量磁化曲线计算剩磁的大小,但该方法需要用到磁化设备进行操作,且对环境和设备的要求比较高[3]。文献[4]以变压器铁芯的暂态电流为切入点,利用暂态过程中电流的时间常数和剩磁之间的关系,提出了基于时间常数的剩磁测量方法。文献[5]指出测量系统研发重点放在提高精确度和在线监测能力上,而忽略了它在各种环境下的可操作性。本文设计了一种以DSP为核心处理器的剩磁测量系统,该系统将暂态电流信号输入DSP进行相关的数据处理和计算,得出剩磁的方向和大小,然后通过串口通信将数据发送到串口触摸屏和上位机。

1 暂态电流测量剩磁的基本原理

在变压器的合闸瞬间,无论是单相还是三相,变压器铁芯中的剩磁就是此刻铁芯中的磁通,由于变压器铁芯中的磁通是不能突变的,因此这个数值无法通过电磁感应定律进行直接测量或者计算[6]。为了解决这一问题,本文首先对电路进行等效处理,等效电路图如图1所示,由于变压器铁芯的磁导率高于空气的磁导率,等效处理时可以忽略空气间隙的漏磁[7];在实验频率小于谐振频率的情况下,电感效应起主导作用,感抗远大于容抗,故不考虑电容效应。在变压器二次侧开路的情况下,通过电路角度分析暂态电流和剩磁之间的关系,当直流激励施加给绕组时,根据基尔霍夫定律得出电路中流过变压器绕组的暂态电流i(t)满足的方程和表达式如下：

(1)

(2)

式中：RL由电源内阻和串联限流电阻组成,Ω;RT为绕组的电阻,Ω;Lm为等效励磁电感,H;R为RL和RT之和,Ω。

图1 实验测量等效电路

根据有限元仿真得到的数据绘制施加激励时不同剩磁情况下的暂态电流,如图2所示。通过分析发现,不同剩磁情况下的暂态电流的变化速率不同,而时间常数可以反映暂态过程中物理量变化的快慢,其定义为电感与电阻的比值,因此可以间接得到暂态过程中时间常数与剩磁之间的关系;通过比较图2(a)和图2(b)可以发现,当施加反向激励时,不同剩磁下的暂态电流变化非常小,曲线可以认为是重合的,因此时间常数的变化也不明显,这表明在测量暂态电流大小之前需要先判断各相铁芯的剩磁方向,然后再同时施加正向激励以测量三相暂态电流。

(a)施加正向激励不同剩磁的暂态电流

(b)施加反向激励不同剩磁的暂态电流图2 施加正反激励的暂态电流图

2 系统总体设计

本文介绍了一种三相变压器剩磁测量系统,其主控芯片选用了TMS320F28335,该芯片具有高度集成的多种外设,其中主要包括CPU定时器、增强型模数转换器模块、3个串行通信接口模块(SCI-A,SCI-B,SCI-C),以及多达88个可以单独编程的多用途复用通用输入输出(GPIO)引脚[8]。基于TMS320F28335的采集系统总体结构框图如图3所示,主要由电源、采集信号、存储器、串口通信4个部分组成,其中电源部分主要用于满足DSP和串口触摸屏的用电需求;采集信号部分主要依靠模数转换器模块的3个通道来采集三相铁芯中的暂态电流;存储器部分主要包括存储临时数据的SRAM芯片和存储代码、常量数据的Flash芯片;串口通信部分主要使用了串行通信接口模块SCI-B和RS232通信方式。

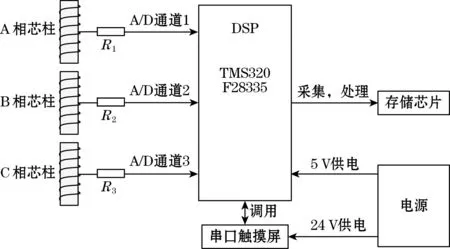
图3 采集系统总体结构框图

三相变压器剩磁测量系统使用了三路A/D采集通道,由于DSP只能接受0～3 V的电压信号,因此需要将三相铁芯上的暂态电流信号经过采样电阻传输给DSP芯片,采样电阻起到将暂态电流信号转换为电压信号的作用;接着,DSP芯片执行已经编译完成的滤波、非线性拟合和计算的相关程序,并将处理后的数据临时存储到相应的存储芯片中;最后,通过双向通信实现DSP和串口触摸屏之间的数据交互,通过在串口触摸屏上进行点按操作,下发指令给DSP,随即DSP将调用存储在存储芯片上的相关信息,并通过SCI-B串口发送给串口触摸屏,以实现数据和曲线的的动态显示,从而完成整个系统的功能。

3 硬件电路设计

3.1 A/D采集模块

变压器铁芯中的暂态电流是模拟信号,因此系统需要利用模数转换器(ADC)将模拟信号转换为数字信号,这个过程包括采样、保持、量化和编码4个步骤。

主控芯片TMS320F28335中内置了一个ADC,这样做的主要原因是降低成本、节省空间、提高集成度和提高系统的总体效率,并避免外置ADC会带来需要处理更多的信号干扰和时间序列等问题[9]。内置ADC和芯片的其他模块使用相同的电源和时钟,因此它不易受到外界的干扰。此外,内置ADC无需外部电路的支持,极大地简化了系统的设计和调试过程。内置ADC可以提供12位的精确度,其分辨率为采集模拟量最大值的1/4096,而且它可以提供1 MSPS的采集速率,能够满足高速数据采集的需求;它内部具有2个8通道的模拟多路开关,分别控制8个通道信号的切换,依靠这些模拟多路开关实现多通道的数据采集;它具有2个采样保持器,功能可以理解为信号处理中每次对模拟信号进行采样时,开关闭合的时间,这也是信号可以同时采样的关键。因此,内置ADC极大地节省了多通道信号采集的时间。

本设计选用顺序采集模式,图4为数据采集状态图。ADC会按照指定的顺序对3个通道进行采集,每次转换完成后,会将采集的数据存储到结果寄存器中。这个过程包括4个步骤：设置ADC采样率,并启用ADC模块;配置ADC采集的通道顺序和数量,并启动ADC转换;通过轮询ADC结果寄存器组的标志位RDY判断转换是否完成;读取ADC结果寄存器中的数据并进行后续处理。

图4 数据采集状态图

3.2 存储模块

在DSP的存储模块设计中,主要使用了Flash存储器和SRAM,FLASH存储器具有非易失性,可以在断电后保持存储内容不变,所以通常用来存储程序代码、数据和配置信息等,但访问速度相对较慢;SRAM具有易失性,存储内容需要在持续供电的情况下才能保持不变,但访问速度非常快,通常用于存储中间计算数据、堆栈和缓存等临时数据[10]。

TMS320F28335的内部已经高度集成了256K×16位的Flash和34K×16位的SRAM,但为了进一步提高系统的性能和可靠性,在外部接口XINTF上连接具有外部存储功能的FLASH芯片SST39VF800和SRAM芯片IS61LV25616,存储模块的硬件设计图如图5所示。这些外部存储芯片通常具有更高的存储密度和较低的成本,因此可以允许运行期间动态更新存储内容,从而提高了DSP的灵活性和可靠性。

图5 存储模块硬件设计图

4 软件程序设计

数字信号处理器(DSP)编程通常涉及大型数据集实时执行复杂的数学运算。因此,C语言编程常被应用于DSP的编程中,原因在于它可以提供对内存使用的高效控制、高效的数据处理和更快的执行时间[11]。

DSP编程选用C语言的原因主要如下：首先,C语言提供了高效的内存管理功能,可以直接访问内存;其次,C语言是一种低级编程语言,这意味着它可以对硬件资源进行直接访问,从而保证DSP实时操作的可行性;此外,C语言具有很强的可移植性,可以在不同的硬件平台和操作系统之间移植代码。C语言可以为DSP编程提供了强大而灵活的工具集。

4.1 方向判断流程设计

外部中断是一种常用于触发信号识别的中断方式,其中激励信号的上升沿作为触发信号[12]。当程序逻辑进入方向判断子程序后,等到外部触发信号,也就是某个方向的激励信号被施加后,开始将采集的数据存储在一个数组中,等待采集到足够的数据后,撤销该方向的激励信号,并等待另一个相反方向的激励信号被施加后,再将采集的数据存储到另一个数组中。当2个数组都采集到足够的数据后,对2组数组进行对比,找到剩磁的正方向。

有2种比较方法可用于确定剩磁的正方向,如图6所示。图6(a)的原理以电流为基准值比较时间常数的大小关系,先找到暂态电流的稳态值,再根据稳态值计算出时间常数对应的电流,从而找到时间常数,时间常数较小的就是剩磁的正方向;图6(b)的原理是以时间为基准值比较电流的大小关系,直接对比2组数组中第n个点对应的电流,电流较大的就是剩磁的正方向。后者这种方法极大地简化了计算过程,同时减小了实验中计算过程带来的误差。

(a)对比时间常数

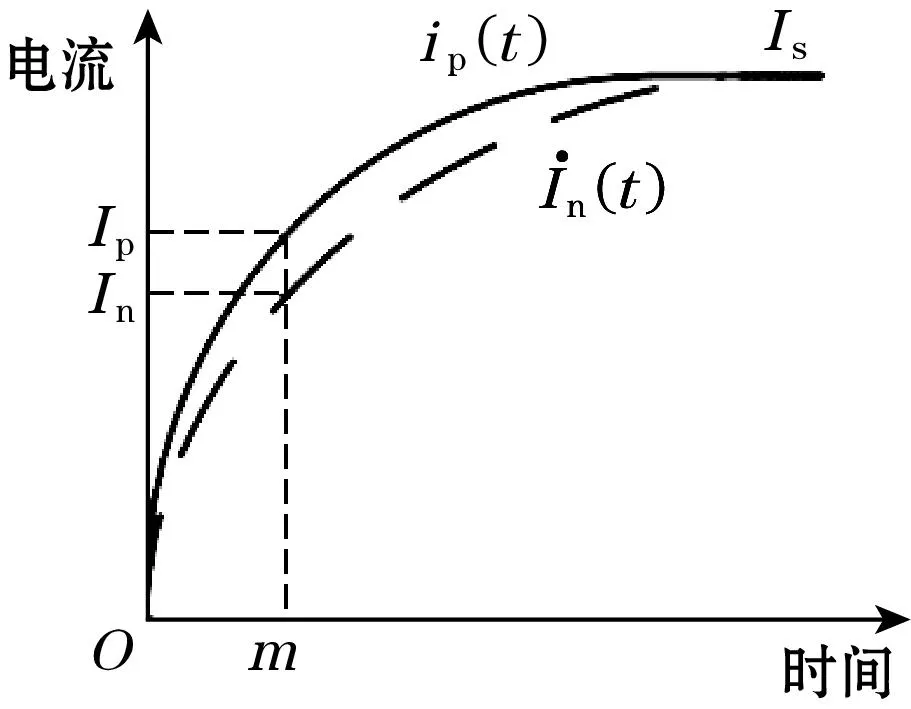
(b)对比电流

4.2 数据采集流程设计

图7为数据采集的软件流程图。首先,将系统连接至变压器铁芯绕组上,系统上电后执行DSP初始化操作,并进行配置串口、配置定时器和A/D初始化等操作;紧接着需要判断采集的点是否有效,因为在暂态电流开始上升之前,正常情况会出现一段暂态电流为0的数据段,由于元器件之间的电磁干扰、电源电压不稳定等因素,这段恒为0的数据段会出现细微的噪声波动,这会极大地影响有效信号的采集和曲线的拟合,为了避免这些问题,采集时需舍弃这段数据;当采集的数据点开始有效后,会将每个点的数据存储到SRAM芯片中;当每个通道采集足够数据点后,DSP执行预先设计的非线性曲线拟合程序进行数据处理,并将处理完成的数据存储至SRAM芯片;等待串口触摸屏发出相应的指令后,DSP将SRAM芯片中相应的数据发送至串口触摸屏上并进行显示,直至试验结束。

图8为有无判断采集点有效这一步骤的2种拟合效果图,对比图8(a)和图8(b),在没有判断步骤的情况下,观察到拟合后曲线零点位置横轴本应在0.01 s,随后曲线上升,但现在直接在0 s后上升,产生了很大的零点漂移。此外,相比于图8(b),图8(a)不仅不能很好地拟合出暂态电流为0的效果,而且暂态电流上升和稳态的拟合效果也远不如图8(b)。因此,判断采集点的有效性对于流程设计是非常有必要的。

5 非线性拟合的算法以及优化

实验过程中存在多种可能引起噪声的因素,例如元器件之间的电磁干扰、电源电压不稳定等,这些噪声会使得采集系统采集的数据存在误差,影响后续计算的准确性,因此需要采用数据拟合的方法提高准确度[13]。

5.1 拟合的运算流程

根据暂态电流的数据特性,本研究采用拟合模型y=a(1-e-bt)+c(1-e-dt),以描述随时间变化的暂态电流曲线。针对这种具有指数特征的非线性拟合问题,在拟合过程中应该注意确保在指数增长或者下降的相应区域上分布均匀,否则可能导致拟合结果不准确或者拟合的效果发散。

(a)不经过处理直接拟合

(b)判断数据有效性后拟合图8 有无判断数据有效性的拟合效果图对比

拟合模型y=a(1-e-bt)+c(1-e-dt)是一个由a、b、c、d确定的非线性函数,为了更高效地进行非线性拟合,可以使用最小化残差平方和的方法。这种方法包括以下4个步骤：

第1步,定义残差函数如下：

γi=yi-a(1-e-bti)-c(1-e-dti)

(3)

式中：yi为第i个数据点的观测值;ti为对应的自变量。

第2步,构造目标函数,将残差函数的平方和作为目标函数：

(4)

第3步,计算雅可比矩阵,雅可比矩阵是一个N行4列的矩阵,其中N表示数据点的数量,第i行第j列的元素：

(5)

式中Pj为第j个参数。

雅可比矩阵可以通过以下公式计算：

(6)

第4步,通过迭代优化的方式,不断更新参数a、b、c、d以最小化目标函数。常用的优化算法包括Levenberg-Marquardt(LM)算法、拟牛顿法、高斯牛顿法等。

5.2 Levenberg-Marquardt算法

在包含指数函数的非线性拟合中,最常用的优化算法是Levenberg-Marquardt(LM)算法[14]。在LM算法中,Hessian矩阵的近似值是通过牛顿法和高斯牛顿法的加权和计算得到的,可用于计算优化目标函数的梯度,进而确定下一步的搜索方向。

参数向量由4个参数组成,利用初始参数和雅可比矩阵计算Hessian矩阵,近似Hessian矩阵可以通过以下公式计算：

H=JTWJ+λI

(7)

式中：H为近似Hessian矩阵;J为雅可比矩阵;W为权重函数;λ为控制步长的参数;I为单位矩阵。

W为N行N列的对角线矩阵。W对角线元素为

(8)

式中σi为第i个数据点的标准差。

在LM算法的迭代过程中,利用梯度向量和Hessian矩阵更新参数,通过计算Hessian矩阵的逆矩阵得到H-1,可以得到参数的更新方向Δp：

Δp=-H-1g

(9)

式中g为梯度向量。

g定义为

g=JTWγ

(10)

在非线性拟合中,计算近似Hessian矩阵是一个关键步骤,因为它影响着算法的收敛速度、稳定性和参数的估计精度。近似Hessian矩阵描述了目标函数在参数空间的局部几何形态,能够用于确定下一步的搜索方向,从而加速优化过程的收敛。在LM算法中,当步长较大时,近似Hessian矩阵起到了类似于牛顿法中的海森矩阵的作用,能够提供更准确的梯度信息。当步长较小时,近似Hessian矩阵起到了类似于梯度下降法中的梯度的作用,可以避免步长过大导致优化过程发散。

5.3 迭代计算及算法的优化

在迭代计算的过程中,主要对当前参数下的雅可比矩阵、近似Hessian矩阵、梯度向量和误差进行计算,并根据误差的情况更新步长,步长更新后,参数向量也随之变化,如果更新后的误差变小,则接受更新的参数,继续迭代;如果更新后的误差变大或者不变,则需要拒绝更新的参数,保持原来的参数,缩小步长,继续迭代。迭代过程直到误差很小或者参数已经收敛的情况,则迭代停止。然而,仅仅依赖步长不足以达到全局的最优解,有一定的局限性。因此,在算法中引入了退火调节,图9为加入退火调节前后参数对比,可以在步进与速度之间综合优化,极大地提高了拟合的效率[15]。

退火调节是一种随机优化算法,被广泛应用于参数优化和函数拟合等问题中。在退火调节中,接受新的参数值的概率与当前温度以及新的拟合指标与旧的拟合指标之间的差距有关,差异越小,接受概率越高。这个特点使得退火调节可以避免陷入局部最优解,使拟合结果更接近全局最优解,而且有助于全局搜索,提高优化效率。

针对非线性拟合的程序,本文进行了进一步的优化：首先,针对不同的曲线选择不同的自适应初值向量,提高了算法的效率和准确性;其次,设置了合适的停止迭代准则,当连续几次迭代后的损失函数变化小于一个设定的阈值时停止迭代;此外,添加了梯度向量的范数,如果梯度向量的范数足够小,说明此时目标函数已经非常接近最优解,算法可以停止迭代。图10为优化前后的拟合效果对比图。

(b)优化后的拟合效果图图10 优化前后的拟合效果图

6 系统测试及验证

为了验证本系统在实际测量中的可行性和准确性,本文将示波器测量的暂态电流数据和本采集系统测量的实验数据进行对比分析。搭建的实验测量平台如图11所示,使用信号发生器生成3个不同的输入激励信号,并用电流探头(N2782B)和示波器(DSOX6004A)测量三相铁芯中实际的暂态电流波形,传给上位机进行显示并计算出实际的时间常数;接着,采用相同的激励信号输入到采集系统中,通过DSP的采集模块、通信模块和事先编译的数据处理程序,最终在串口触摸屏上进行相关参数的显示,方便进行后续的分析。

图11 实验测量平台

图12(a)显示了三相变压器中各相铁芯中暂态电流的实际测量波形,图12(b)为经过数据处理和拟合之后的光滑曲线。通过进行数据处理的拟合,可以减小噪声对时间常数的影响,并简化了时间常数的计算过程。这种处理方式不仅可以提高实验数据的可读性,还可以减小误差的影响,从而提高系统的测量准确性。

(a)三相变压器暂态电流的实际测量波形

(b)三相变压器暂态电流曲线的拟合图图12 三相变压器暂态电流的实验波形

根据表1的分析结果可以发现,测量得到的数据经过数据拟合再计算时间常数的误差明显小于直接计算。而且在暂态电流较小的情况下,测量系统计算的时间常数存在着一定的误差,该误差可能源于3个方面：第一,测量仪器的精度不足,当电流非常小时,可能无法准确识别电流的变化;第二,环境的干扰会对小信号的测量产生影响,并且小信号受干扰的可能性较大;第三,测量误差累积,由于小电流的变化相对于大电流较小,因此需要更高的测量精度来捕捉这些变化,测量误差也更容易积累,从而影响测量结果的准确性。

表1 本系统与示波器测量数据对比

考虑到测量系统中数据的采集以及后处理的误差,认为上述误差是在可以接受的范围之内。此外,由于变压器可能存在于各种环境中,示波器不仅不便于携带,而且户外环境下可能无法使用适配的电源。相比之下,本文设计的测量系统小巧轻便,供电模块简便。与示波器单一的显示功能不同,本系统可以快速地计算出变压器相应的参数并进行相关物理量的动态显示。经过测试,各模块都可正常使用,达到了预期的设计目的。

7 结束语

为了能够准确、快速地在线检测变压器的剩磁,本文设计了一种基于暂态电流的剩磁测量系统。通过运用串口通信、迭代算法和数据处理等技术,最终实现在串口触摸屏或者上位机上显示结果。通过与示波器等设备进行对比,验证了数据采集的准确性。该系统能够实现对变压器参数的在线监测,体积相对传统的测量设备较小,加上便携式电源可以实现户外工作。因此,它可广泛应用于大多数环境下的变压器参数的测量。