航空齿轮薄辐板车削加工变形预测及切削参数优化研究
2024-01-22宦海祥王孟雄张可
宦海祥,王孟雄,张可
(盐城工学院 机械工程学院,江苏盐城 224051)
在航空航天领域,保证飞行器足够推重比的条件下,尽可能地减轻其零部件的重量,是重点发展的方向之一。齿轮薄辐板在航空发动机零部件中应用广泛,具有重量轻、转速高、载荷重的特点。航空高性能齿轮由于壁厚薄,在生产过程中存在刚性弱等问题,材料多使用高硬度、难加工的碳素钢和合金钢,其切削加工过程中极易产生变形、平行度和圆周度偏差过大等问题,这会导致齿轮轮毂区域出现偏心引起齿轮不平衡的振动,特别是辐板车削轴向变形较大,加工精度控制困难。为确保航空齿轮的加工精度,必须对加工变形进行控制[1-2]。
近年来,国内外诸多学者从各方面对薄壁件加工性能和工艺优化进行了深入研究。加工性能方面,在对薄壁件变形研究加工结束后工件变形产生的影响,相比于初始残余应力,切削残余应力对于变形的影响较大[3]。Masoudi等[4]通过测量工件上的残余应力,研究残余应力与变形之间的相关性,结果表明力和温度对薄壁零件的残余应力和变形有直接影响。在考虑薄壁齿轮和空心轴的齿轮动力学模型中,采用壳单元代替梁单元和集中质量单元建立齿轮-轴有限元模型[5],防止简化薄壁结构,导致过大的临界速度。王大勇[6]建立了薄辐板结构的齿轮模型,根据动力学方程及载荷分配求解单个轮齿上的载荷历程,并依据啮合时间进行加载,模拟了齿轮正常工作条件下的受力状态。工艺优化方面,廖凯等[7]对航空铝合金薄壁构件的几何形状和加工表面应力进行研究,运用变形解析函数对薄壁构件加工变形程度进行预测性计算和分析,结果显示,薄壁构件变形挠度与理论计算值偏差为312 μm,偏差处于变形不确定度范围内,解析函数准确性得到验证。Li等[8]通过实验测量薄壁件加工后一定时间内的变形规律,提出一种基于提高等效弯曲刚度的薄壁件加工变形控制方法。
Chen等[9]建立了一个动力学模型来预测薄壁零件加工变形,使用迭代计算考虑了切削力与加工变形之间的耦合关系。李承然等[10]基于温度场-渗碳场-组织场-应力应变场多场耦合模型,运用有限元仿真分析对AISI9310钢薄辐板齿轮的热处理过程进行了数值模拟,分析淬火过程轮齿组织与应力演变规律及冷处理和回火过程对轮齿组织含量和应力大小的影响,得到了齿轮热处理后最终的残余应力和变形。丛靖梅等[11]提出了基于工况映射与薄壳应力贴合的残余应力变形的仿真预测方法,实验结果表明该方法能够有效预测薄壁件的加工残余应力变形。研究人员对齿轮各个部位的结构优化开展了较多的研究,但有关齿轮薄辐板的加工变形控制方面的文献较少。现有的文献多数采用实验法在工艺上做工艺方案改善,缺乏针对薄壁辐板加工变形开展的研究[12-15]。高性能齿轮生产过程中关于辐板较薄、切削时易变形、尺寸精度难以控制等问题的研究还有所欠缺,对于切削参数优化多数基于仿真实验设计,缺少进行相关试验验证[16-18]。
本研究基于ABAQUS仿真平台,对航空齿轮钢18Cr2Ni4WA[19]的切削过程进行有限元模拟,开展切削仿真研究,通过建立三维动态切削仿真模型,采用正交实验设计,研究不同切削参数下的切削力以及加工变形量;根据切削力与切削参数的对应关系,获得切削参数与工件变形量之间的对应关系,进行了加工工艺参数的优化研究;并运用静态仿真分析,研究了切削力和夹紧力的叠加对薄辐板加工变形的影响;最后对仿真结果进行了极差分析,通过试验的方式对仿真结果进行了验证。
1 齿轮薄辐板模型
1.1 齿轮模型
鉴于目前多数航空齿轮都会采用薄辐板的形式,本文基于某发动机附件传动齿轮作为研究对象,对其车削加工工序引起的加工变形规律进行研究。薄壁齿轮的关键尺寸如图1所示,整体直径为120 mm,齿厚为20 mm,轮毂直径为29 mm。辐板加工区域直径为100 mm,齿胚辐板加工前厚度为10 mm,使用三爪卡盘夹持,加工后厚度为3 mm。
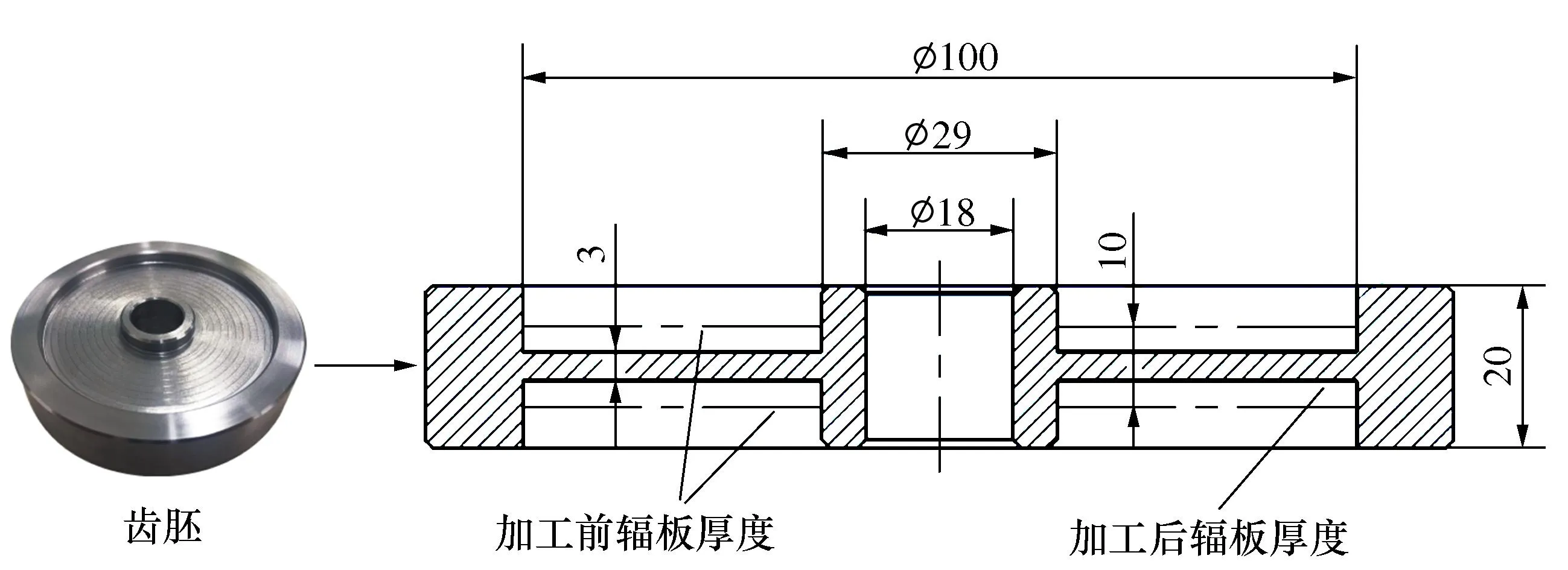
图1 齿轮薄辐板加工简图Fig. 1 Gear thin spoke plate machining
1.2 材料物理特性和本构模型
本文所研究的薄壁辐板齿轮材料为强度高、韧性好和淬透性好的中碳钢18Cr2Ni4WA,该材料经过复杂的化学热处理后,坯料心部硬度达到HRC31~HRC41,表面硬度不低于HRC60,以确保齿轮表面有较高硬度且心部呈现一定的韧性。然而,这也会给材料的切削加工带来一定的困难,切削时表现出切削力大、切削温度高,表面容易产生硬化现象,消耗功率大、摩擦剧烈、刀具磨损快等特点。
本构模型是金属材料切削仿真模拟材料大塑形变形的关键,具有代表性的是Johnson-Cook(J-C)本构模型和Zerilli-Armstrong模型,两个本构模型都引入材料的应变硬化、应变率硬化和热软化参数。Zerilli-Armstrong模型主要运用在体心立方及面心立方金属,同时针对不同的晶体结构有着不同的表达形式;J-C本构模型是使用经验作为主要参考来源的本构模型,主要针对的是大应变、高应变率、高温变形的材料,同时也能运用在各种晶体结构。J-C本构模型的温度适用范围很广,从室温到材料熔点温度范围内都是有效的。三项乘积分别对应了应变硬化、应变率硬化和温度软化对材料流动应力的影响,适合用来模拟高应变率下的金属材料。因此,综合以上因素的比较,本文选用J-C本构模型来表达材料的本构关系,用连乘的方法关联,综合反映变形热力参数之间的数量关系,其表达式为
(1)
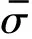
18Cr2Ni4WA材料的J-C本构参数[20]如下:A=1 010 MPa,B=1 409 MPa,C=0.04,n=0.67,m=1.2。物理、力学、热学参数见表1。
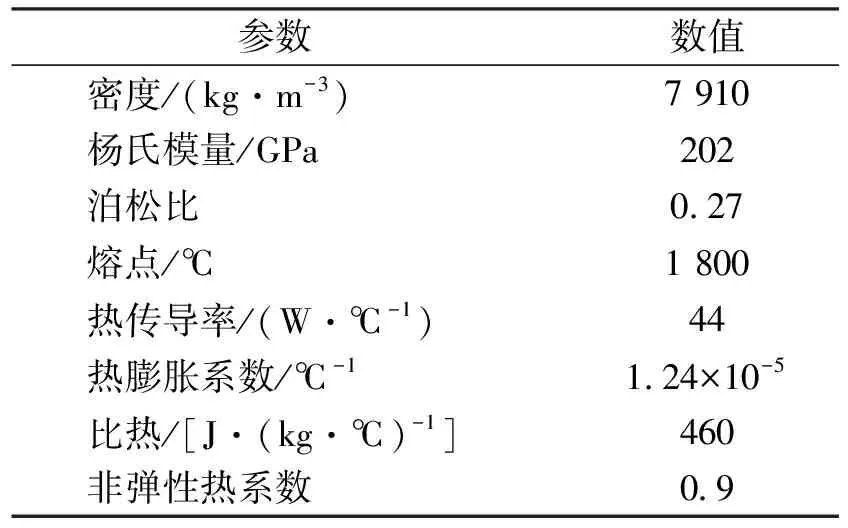
表1 18Cr2Ni4WA的物理、力学、热学参数[20]Tab. 1 Physical, mechanical and thermal parameters of 18Cr2Ni4WA[20]
2 研究条件与方案
2.1 刀具选择与切削方式
齿轮辐板具有深槽结构,使用普通外圆车刀加工会出现可达性差的问题,故选用端面切槽刀配合专用的端面切槽刀杆(见图2)作为加工刀具组合,其中刀具选取金属陶瓷刀具(C型金属陶瓷刀片Al2O3+ZrO2)。端面切槽在粗加工阶段采用轴向进给的车削方式,首刀从最大直径处开始向内加工,这一步需要产生连续切屑避免在窄槽中堵屑,特殊情况可以采用啄进式加工或人为设置暂停的方法。首刀后的每一刀设置为背吃刀量ap的0.6~0.8倍,vc为切削速度;f为进给量,具体原理如图3所示。
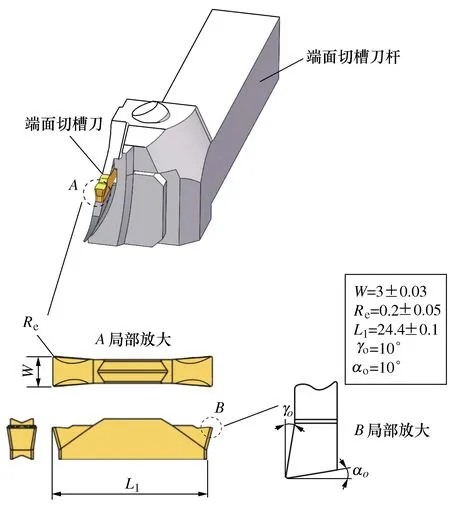
图2 端面切槽刀杆参数Fig. 2 Parameters of end grooving toolholder
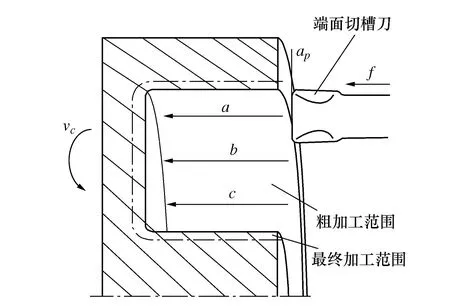
图3 轴向进给加工方式原理图Fig. 3 Schematic diagram of axial feed machining method
2.2 仿真参数
从切削的工艺参数角度考虑,使用单因素实验设计方案来研究3个工艺参数对实际切削力的主要影响,这些参数涉及切削速度vc,进给量f和切削深度w。vc值选取端面切槽推荐范围90~150 m/min,f值选取端面切槽推荐值0.1 mm/r附近的参数,w的推荐值为背吃刀量ap的0.6~0.8倍。
为了充分考察切削三要素对切削力的影响,故每个因素取4个水平,设计三因素四水平正交实验L16(43),试验方案见表2。
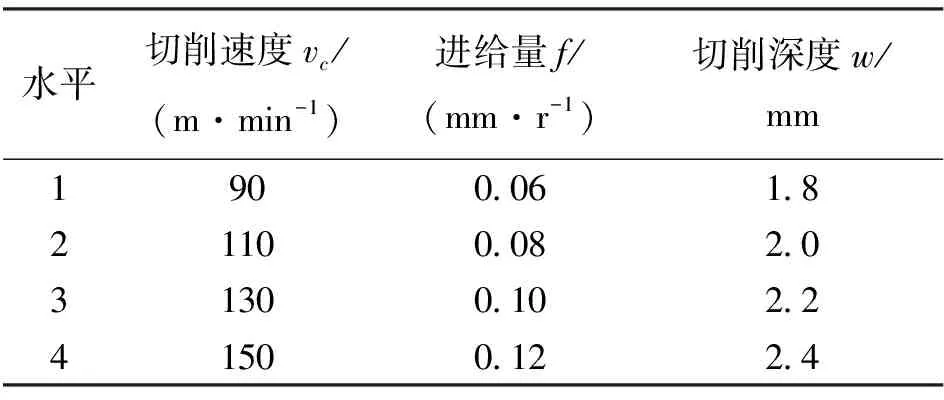
表2 切削仿真L16(43)正交实验表Tab. 2 Table of orthogonal experiments for cutting simulation L16(43)
3 切削有限元仿真与试验
3.1 三维切削有限元模型建立
建立工件三维有限元模型,分别建立切屑层和基体,通过绑定的方式连接在一起。由于齿轮的实际尺寸比较大,在动态切削仿真中将模型材料参数单位设置为m,其中被加工工件厚度0.02 m,切屑层宽为0.015 m,其余位置为基体部分,仿真模型和网格划分模型如图4所示。三维有限元模型网格采用六面体单元,圆周方向网格布种尺寸为0.000 5 m,径向方向网格布种尺寸为0.000 25 m,网格单元类型选择为八结点热耦合六面体单元C3D8RT。仿真采用热力耦合分析步,刀具刚切削工件时,切削力呈现上升趋势,当刀具完全切入工件时,切削力才呈现出平稳状态。为保证刀具能够完全的切入工件,设置三维切削仿真时间及分析步时间为0.004 s。其中,刀具网格划分模型设置为八结点热耦合六面体为主的自由进阶算法,采用单元C3D8RT进行划分,仿真过程不考虑刀具磨损对加工的影响,所以设置刀具为刚体。约束材料基体底部、左侧和右侧边线的自由度;初始温度设置为20 ℃;切屑层与刀具之间的摩擦符合库伦摩擦定律,摩擦因数为0.2,建立三维正交仿真模型。
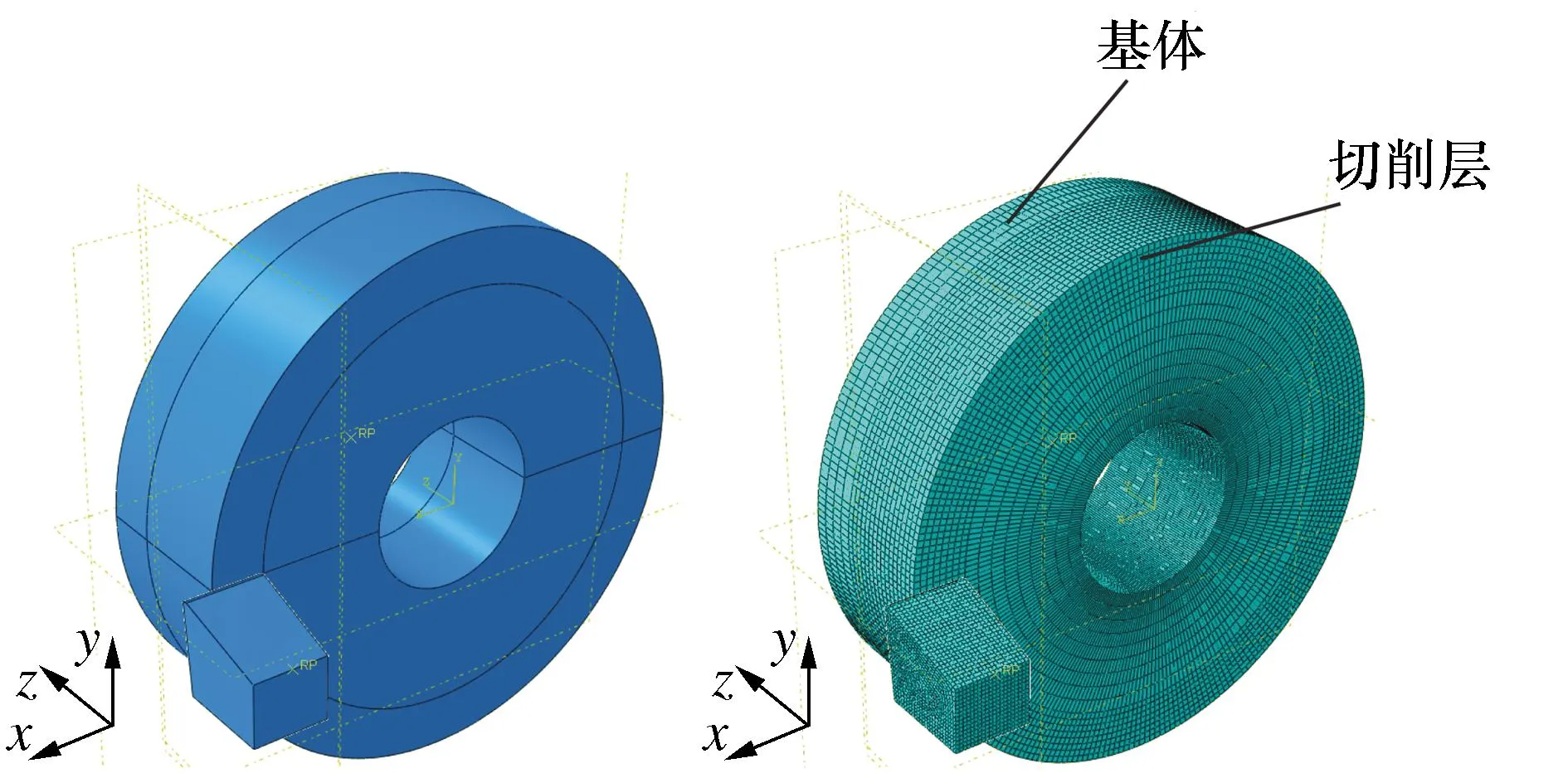
图4 三维仿真模型网格划分示意图Fig. 4 Schematic diagram of meshing of the 3D simulation model
3.2 仿真结果
3.2.1 切屑形貌
以切削速度vc=90 m/min,进给量f=0.06 mm/r,切削深度w=1.8 mm为例,得到的工件切削过程中等效应力分布云图,如图5所示。
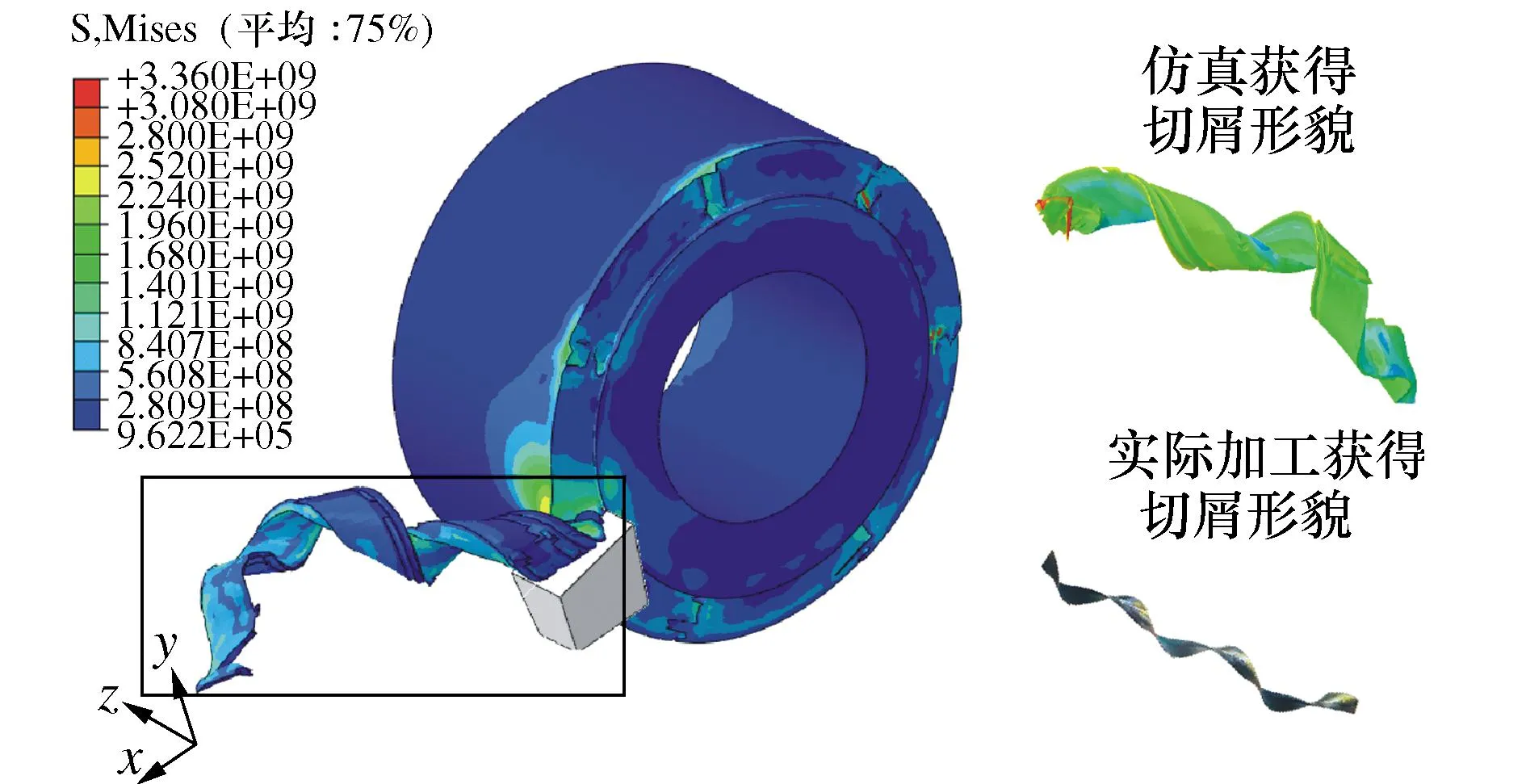
图5 切削过程应力云图Fig. 5 Stress cloud map of cutting process
通过图中特征可以发现,切屑类型为带状切屑形貌,切削层经塑性变形后被刀具分离,并随前刀面流出。有限元仿真过程获得的切屑形貌与实验结果对比,如图5所示。由图5可以知:仿真切屑形貌整体光滑,切屑较长时切屑呈螺旋状卷曲,同时切屑边缘并无明显锯齿状毛刺,这些特征与切屑的实际形貌相吻合,说明仿真结果符合实际加工结果。
3.2.2 切削力
三维切削仿真提取的切削力结果如图6所示。切削力方向以仿真模型方向为主。仿真过程中,随着刀具开始切削,切削力快速增大,随着切削过程逐渐平稳,切削力变化也逐渐趋于平稳,这和实际加工情况相符。当切削过程达到稳定状态之后,切削力连续波动,由于切削过程中第一剪切区的高温引起材料的热软化导致切削力下降。切削热随切削力的降低而降低,迫使热软化效应降低导致切削力增大,因此造成切削力的波动这种影响也反映在有限元模型中。在实际端面切槽加工中,切削深度相对于进给量大的多,吃刀抗力大,所以y方向的主切削力最大。
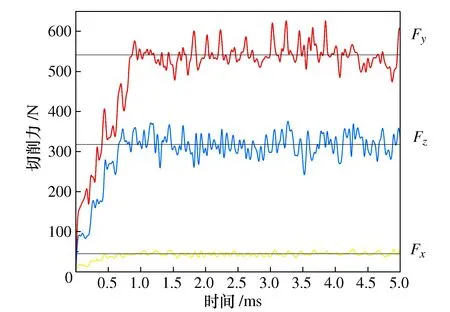
图6 切削力变化曲线Fig. 6 Cutting force variation curve
3.2.3 变形位移
在每一分析步中提取三维动态切削仿真中输出的切削力,依次将切削力载荷分布到走刀路径上的各个结点上,基于有限元求解计算,获取辐板加工变形预测结果。仿真后得到车削加工的变形位移,如图7所示。由图7可知:靠近齿轮轮毂位置变形量最大,辐板切削时切削力过大对轮毂的同轴度有很大的影响。
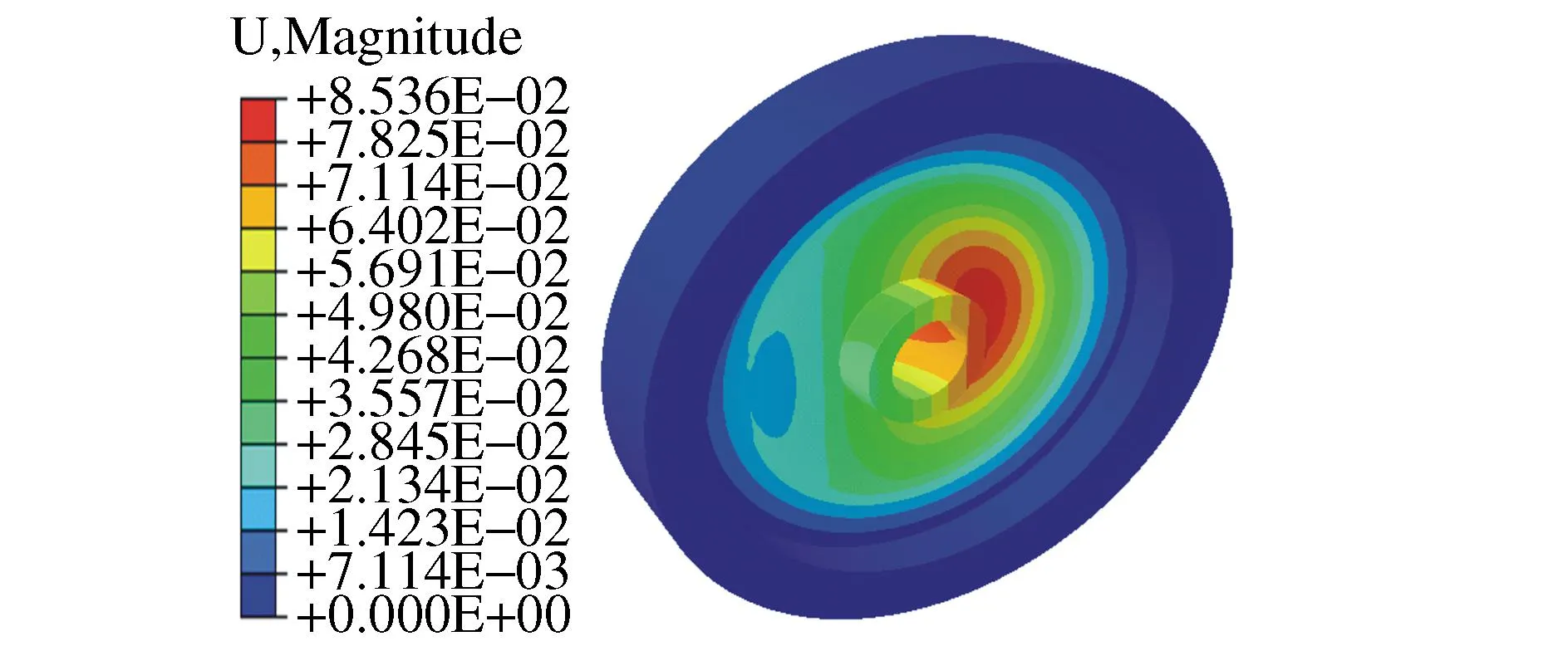
图7 车削加工过程中辐板位移云图Fig. 7 Spoke displacement cloud map during turning process
3.3 试验设计
加工试验开始之前,需要对所有待加工材料进行去应力退火处理,尽量消除工件内部初始残余应力,减小对加工变形试验结果的影响。加工完成后使用三坐标测量仪测量加工零件的尺寸精度,测量设备为ZEISS型号SPECTRUM测量机,使用GOOD FIXTURE定位台进行定位,测量位置为基准面辐板。具体加工测量流程如图8所示。

图8 加工流程及测量方式Fig. 8 Machining procedures and measurement method
4 切削参数优化与试验验证
4.1 正交实验结果
切削力与刀具参考点的作用力的关系为等大反向,故通过刀具参考点输出切削运动方向切削分力Fc、垂直切削运动方向切削分力Ff,经计算得到切削分力在波动稳定区域的平均值。辐板变形量提取预测仿真模型中的最大变形量U,实验结果见表3。
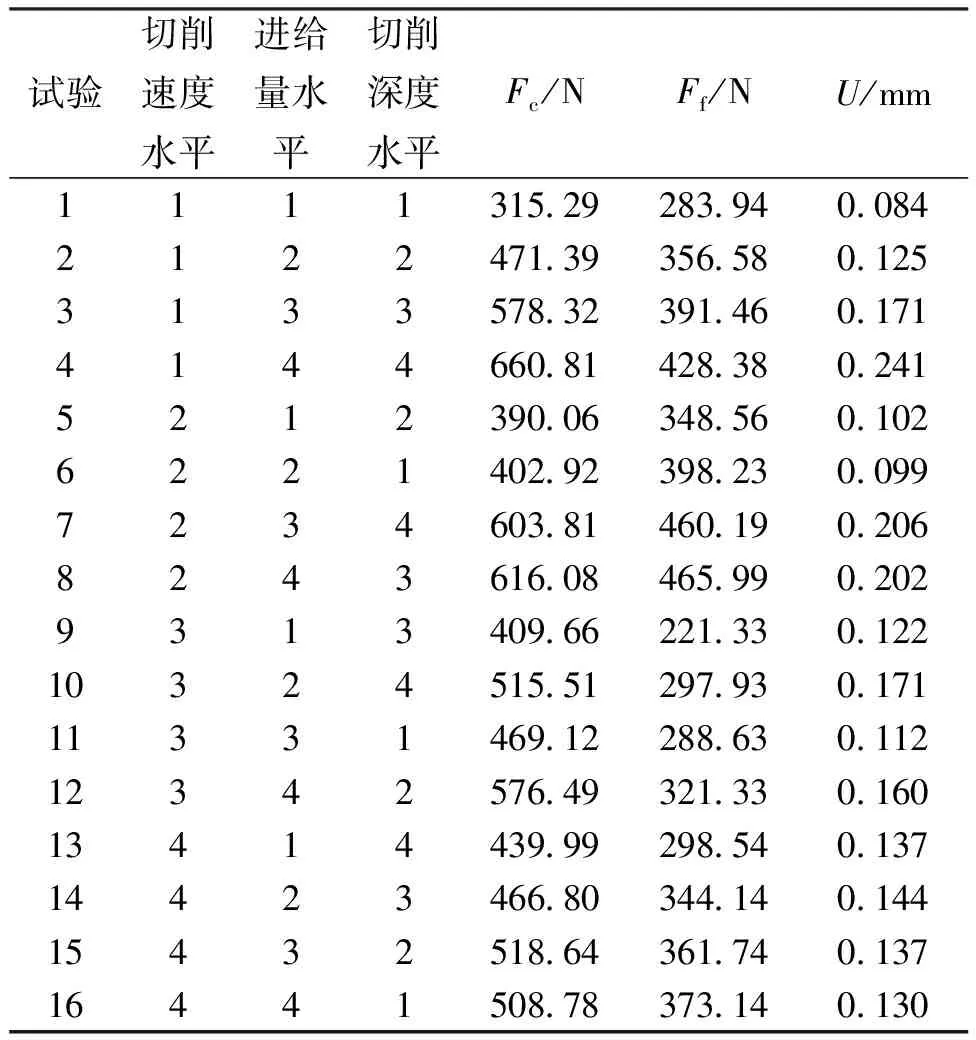
表3 切削力与变形量仿真实验结果Tab. 3 Cutting force and deformation simulation results
4.2 极差分析
极差分析法是一种直观分析法,可以将复杂的多因素数据转变成简单的单因素数据解决问题,转变计算公式为:
Kj=x1+x2+x3+x4
(2)
kj=Kj/g
(3)
R=kmax-kmin
(4)
式中:Kj为所研究因素同等水平条件下对应的试验数据之和(j为水平代号);x1、x2、x3、x4为对应试验数据;kj为对应水平数据平均值;g为水平重复数;R为极差。
经过计算,得到辐板变形量U的极差值,见表4。

表4 辐板变形量U极差分析表Tab. 4 U-pole analysis of spoke plate deformations
辐板变形量U与切削参数的响应关系如图9所示。由图9可知:切削深度是影响辐板变形的主要因素,进给量为次要因素。选取因素的水平与要求的指标有关,研究要求齿轮薄辐板加工变形量U越小越好,则应取最小的那个水平,即取切削速度150 m/min、进给量0.06 mm/r、切削深度1.8 mm为最优切削参数。
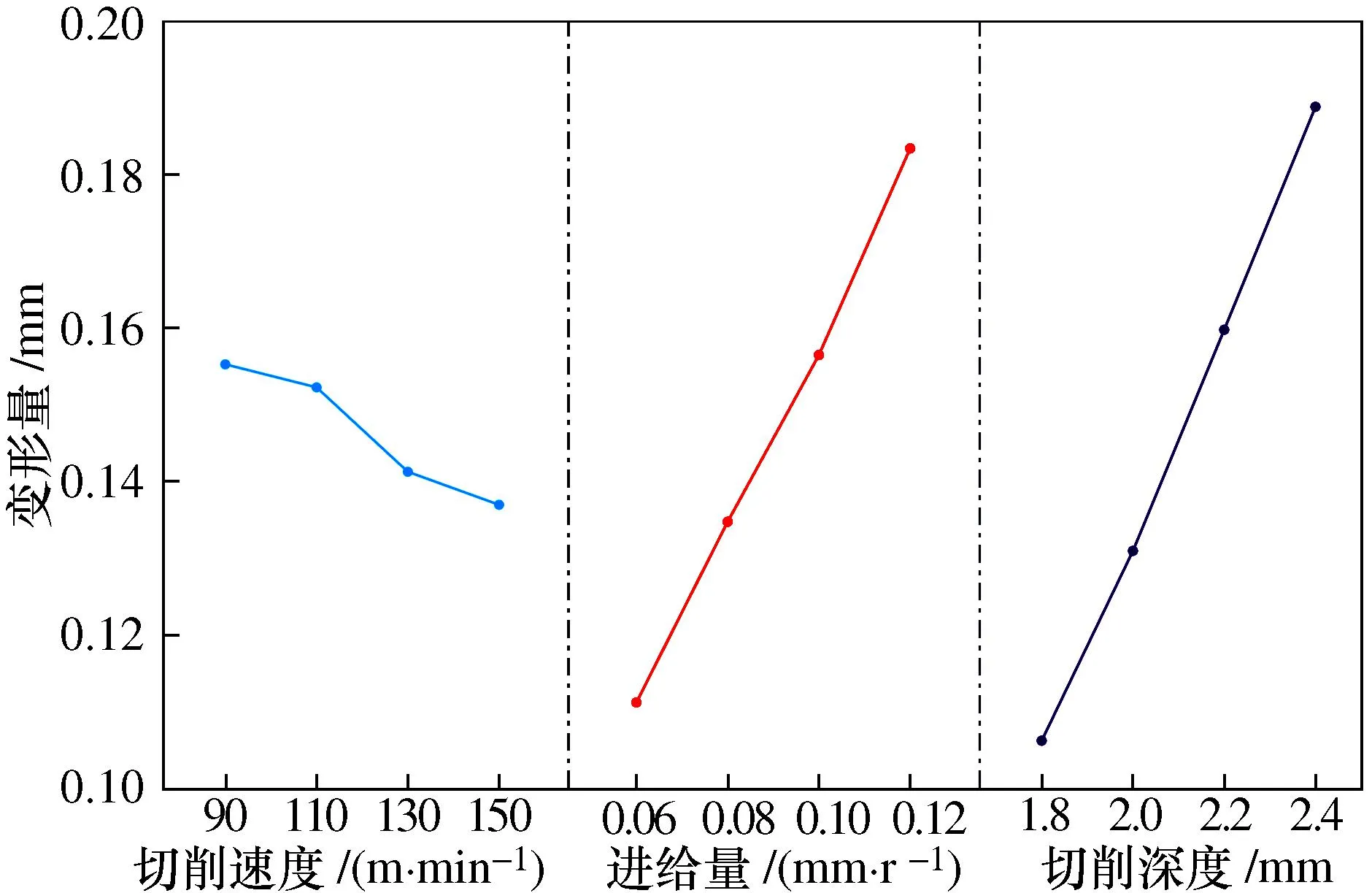
图9 变形量U与切削参数之间的响应关系Fig. 9 Response relationship between deformation U and cutting parameters
4.3 变形量试验验证
采用仿真与试验变形量做对比验证,从三坐标测量仪测量图10可以看出:试验变形量U为0.13 mm,将仿真获得的变形数据与试验获得的变形数据进行对比,最大变形量U的预测误差在10%以下。分析结果表明,预测模型仿真结果与试验加工情况规律一致。
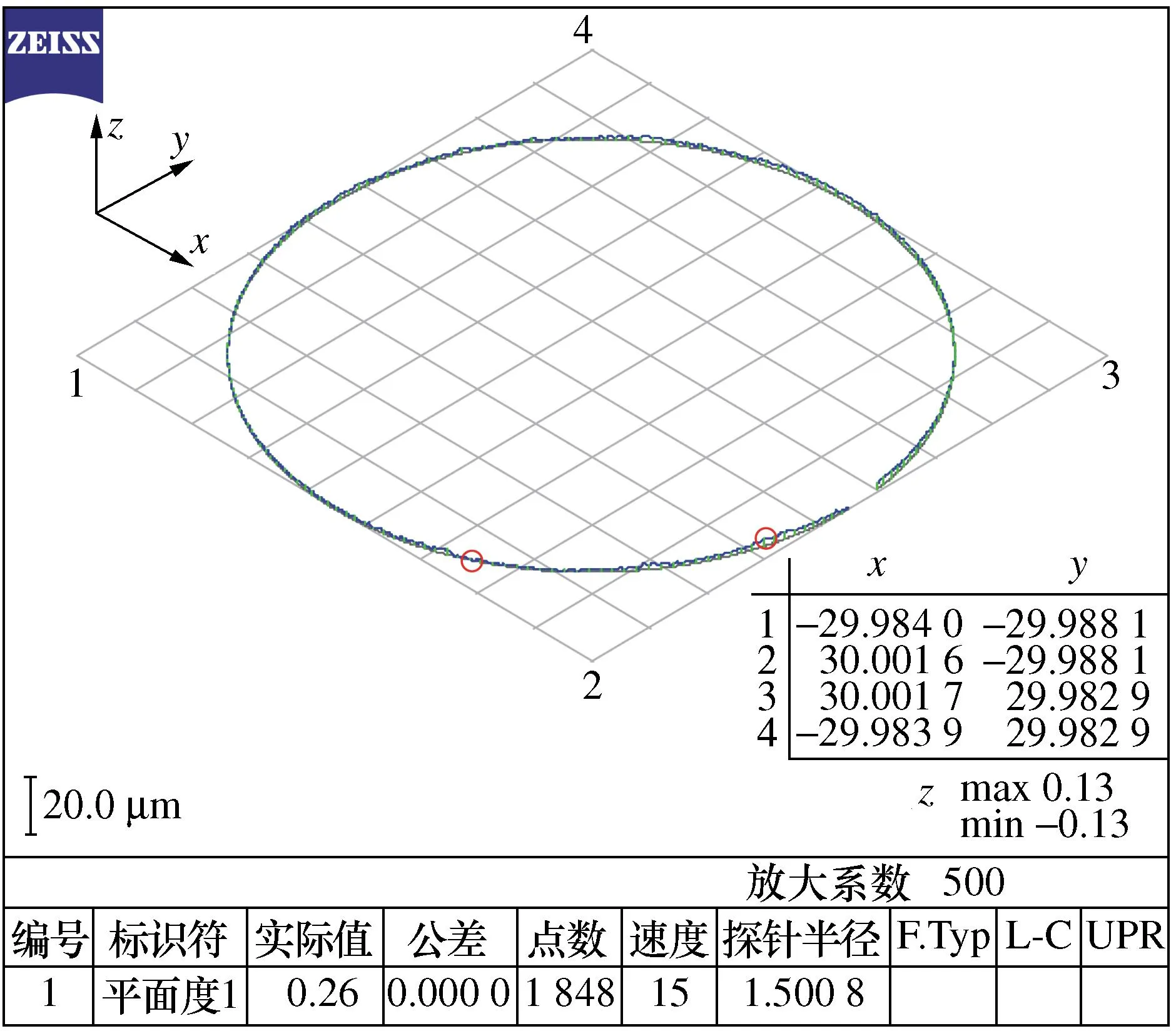
图10 三坐标测量仪测量图UFig. 10 Coordinate Measuring Machine Measurement Diagram U
5 结论
本文基于ABAQUS软件对高强度中合金渗碳钢18Cr2Ni4WA进行三维切削仿真研究,提出了薄壁齿轮薄辐板加工变形预测有限元模型,并通过极差分析获得了最佳切削参数,同时开展试验进行了验证。得出的结论如下:
1) 通过静力学分析实现了齿轮薄辐板加工变形量的预测,基于三维切削仿真获得了切削力参数和切屑形貌,将切削力施加在齿轮模型上以获得齿轮的最大变形量。研究发现,齿轮辐板轴向变形量最大,径向变形在轮毂处最大。
2) 通过设计L16(43)型正交实验仿真,分析了切削三要素对加工过程中切削力的影响,揭示了切削力获得对齿轮辐板变形的影响。并基于极差分析发现,切削深度的选择对辐板变形影响最大,切削深度对切削力影响最大,适当增大进给量、减小切削深度可以减少变形同时提高加工效率。
3) 加工参数优化研究结果表明,切削速度为150 m/min、进给量为0.06 mm/r、切削深度为1.8 mm为最优切削参数,此时齿轮薄辐板加工变形量U最小;并将仿真获得的变形数据与试验获得的变形数据进行对比,最大变形量U的预测误差在10%以下。
