柔性拱承式斜拉桥不对称调索技术
2024-01-21鞠晨星
鞠晨星
(中铁十二局集团第七工程有限公司,湖南 长沙 410004)
近年来斜拉桥在国内外蓬勃发展,现有斜拉桥桥塔形式多采用柱式、A型、钻石型、倒Y型以及H型。拱形塔柱作为一种特殊的斜拉桥桥塔形式,对于斜向跨越既有交通具有较好的适应性,且具有外形美观、构造简单、节省材料等优点[1]。在斜拉桥建设过程中,拉索索力和主梁线形的施工监控及调整是非常重要的一个环节。合理的斜拉桥索力及线形对于斜拉桥具有正常使用功能和承载能力至关重要,而拉索受垂度、温度变化、风力和日照温差、施工临时荷载、混凝土收缩徐变等复杂因素干扰,索力与索形的关系十分复杂[2]。
斜拉桥的成桥状态和索力值与施工阶段紧密相关,如何合理地确定每一施工阶段的张拉索力对后期成桥状态的影响很大[3]。国内外已经提出的索力调整方法主要有迭代法、最小二乘法、弯曲能量(弯矩)最小法、刚性支撑连续梁法、影响矩阵法、无应力状态法[4];梁鹏[5]基于索力优化的影响矩阵法原理,提出一种斜拉桥成桥索力优化的实用方法,并从理论上加以证明,实践上得到检验;叶再军[6]根据无应力状态法理论,提出了以无应力索长为线索确定二次调索施工索力的方法并结合具体工程实例验证了该方法的可行性和准确性。而迭代法[7]的优点在于可以考虑结构的非线性作用,一般迭代15次以内便可以得到理想的成桥索力。
本文以跨越深汕西高速公路的拱承式斜拉桥为背景。由于该桥跨越深汕西高速公路,施工过程中主梁中跨受不对称、不等高的临时支墩影响,且支墩间跨度较大,导致主梁线形不对称且与设计线形相差较大,斜拉索索力不对称,桥塔偏位。本文介绍了如何利用迭代法确定初张拉过程中受不对称支墩影响的柔性拱承式斜拉桥的合理索力及调整线形,通过设置不对称的索力调整值来达到将主梁调平、索力对称的目的,索力与线形双控对该斜拉桥进行二次调索,消除桥塔偏位,即采用不对称调索技术。
1 计算原理
二次张拉阶段,所有斜拉索均存在初始力,所以张拉任何一根索,其它斜拉索均会受到影响。先假定一组索力调整值,按正装计算得到一个成桥状态,将该成桥状态与事先定好的合理成桥状态比较,以此来修正该组索力调整值,再进行新的一轮正装计算,直至收敛为止[8]。采用迭代法计算理论索力:设定{F}为斜拉索索力设计值,设定{F1a}为斜拉索按施工阶段分别施加的初拉力,设定{F1b}为斜拉索张拉后的索力,得到张拉后的索力{F1b}与设计值{F}的差值{Δ1}:
{Δ1}={F1b}-{F}
(1)
计算第一次迭代的误差{δ1}:
{δ1}={Δ1}/{F}
(2)
设定{F2a}为第二次计算初张拉拉力:
{F2a}={F1a}-{Δ1}
(3)
设定{F2b}为第二次计算张拉后的索力,得到第二轮张拉后的索力{F2b}与设计值{F}的差值{Δ2}:
{Δ2}={F2b}-{F}
(4)
计算第二次迭代的误差{δ2}:
{δ2}={Δ2}/{F}
(5)
依此类推,通过多次迭代计算后{δn}≈0,记此时的{Fna}为顺序张拉力值,记{Fnb}为张拉结束的理论索力。
2 工程实例分析
2.1 工程概况
跨深汕西高速大桥线路法线方向与高速公路方向夹角为26°。本桥主桥为(32+160+32)m拱承式斜拉桥,主桥长225.5 m,桥梁顶面全宽16.2 m,结构中心处梁高3.168 m。
本桥的施工工序为:在设计位置拼装桥塔的同时,借助导梁和临时支墩,将钢主梁由广州侧向汕尾侧逐段顶推至设计位置;初次张拉斜拉索;拆除临时结构;浇筑桥面板;再次张拉斜拉索提升主梁高度;施工剩余桥面构造。图1为全桥梁段划分情况,主梁共21个节段,关于桥跨中心对称。图2为临时支墩位置布置,为不影响既有高速公路交通,3号和4号临时支墩皆只布置一座。图3为加劲梁横断面,横断面由钢箱梁和桥面板两部分组成,图中左幅为加劲梁标准横隔板处横断面,右幅为加劲梁标准横断面。图4为桥塔布置,桥塔采用钢结构,共21个节段,关于道路中心线对称。全桥共设置12对斜拉索,梁上索距12 m。索塔锚固采用分散锚固形式,斜拉索采用平行钢丝拉索,空间双索面体系,索塔及索梁采用钢锚箱方式锚固,张拉端设置在主梁侧,通过频率法对每一根斜拉索张拉过程进行测试[9]。

图1 全桥梁段划分(单位:cm)
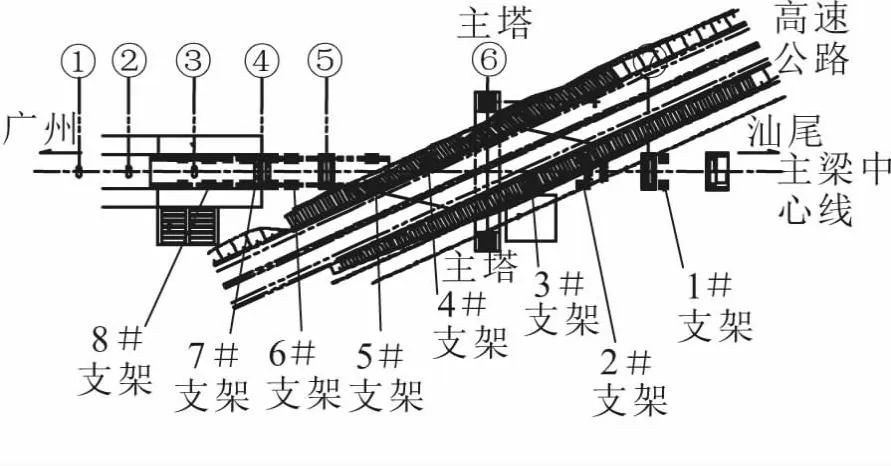
图2 临时支墩位置(平面)

图3 加劲梁横断面(单位:mm)
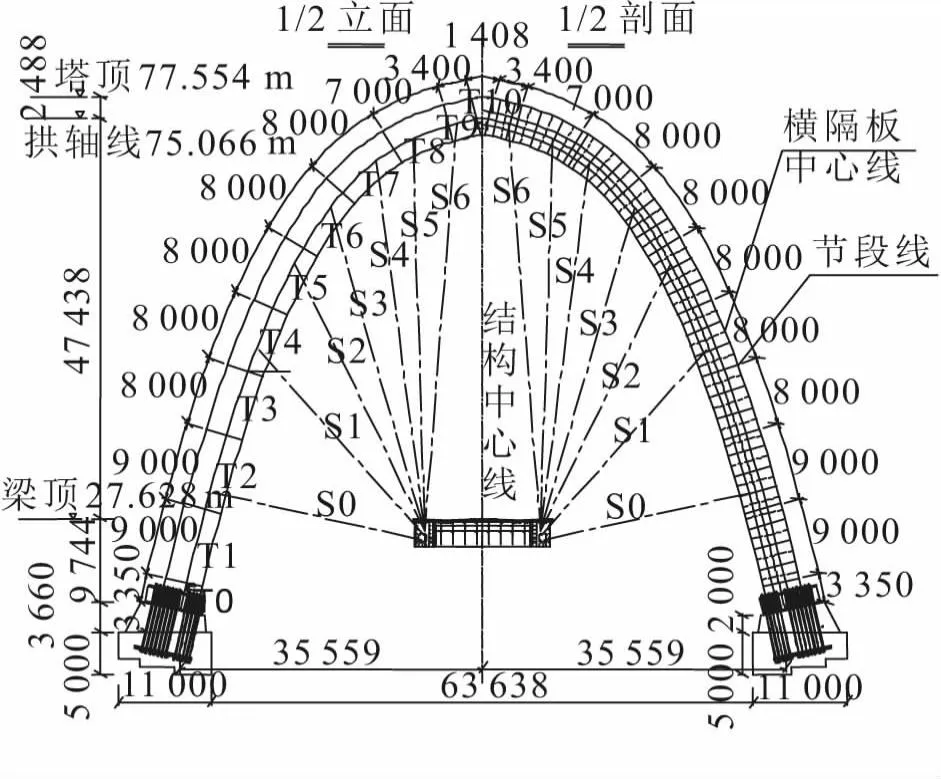
图4 桥塔结构布置(单位:mm)
主梁顶推完成后,按照S6→S0的顺序分批次进行张拉,先张拉4根S6,再张拉4根S5,依此类推。由表1可知,主梁顶推后斜拉索分批次初张拉结果与设计值相差较大,部分斜拉索索力测量值与设计值相差达到20%以上。其原因是该斜拉桥跨越高速公路,主梁中跨受不对称、不等高临时支墩影响,导致主梁实测线形标高低于设计值,桥塔受不对称索力影响产生偏位。为避免对后续施工产生不利影响,保证施工安全,故需要在拆除临时支墩后、浇筑桥面板前对斜拉索进行二次调整。

表1 初张拉拉索索力对比 kN
2.2 数值模拟
借助MIDAS/Civil建立全桥有限元模型如图5所示,主梁和桥塔采用梁单元模拟,斜拉索采用仅受拉桁架单元模拟,共计梁单元285个,受拉桁架单元24个,主塔底部固结,斜拉索两端分别锚固于主塔及主梁钢锚箱上。主梁在两个中支墩处释放纵向转动,两个边墩处释放纵向转动和竖向平动。通过模型进行斜拉索分批次张拉过程的模拟计算。
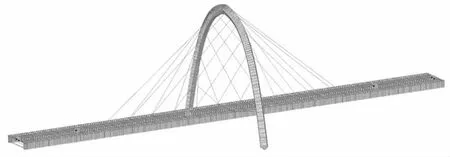
图5 MIDAS有限元模型
2.3 对称调索模拟
本文对施加对称的索力调整值的传统方法进行了数值模拟:基于一个模拟现场桥塔初张拉偏位现状的模型,通过对斜拉索施加对称的索力调整值,按照S6→S0的张拉顺序分批次张拉,如表2所示,求得调索结束后的索力值,发现通过这种调索方式最后得到的斜拉索索力是不对称的,柔性桥塔因受不对称索力的影响而产生较大偏位,幅值达到115 mm,见图6。究其根本原因,当向4根S6拉索施加相同的索力调整值后,4根S5的索力是不相同的,若此时向S5张拉相同的索力调整值,对每根已经张拉结束的S6的影响是不同的,导致S6的索力再次不一致,以此类推,最终使得桥塔依然受到不对称索力的影响而产生偏位。本文结合现场实际情况,引入了柔性拱塔斜拉桥的不对称调索技术。
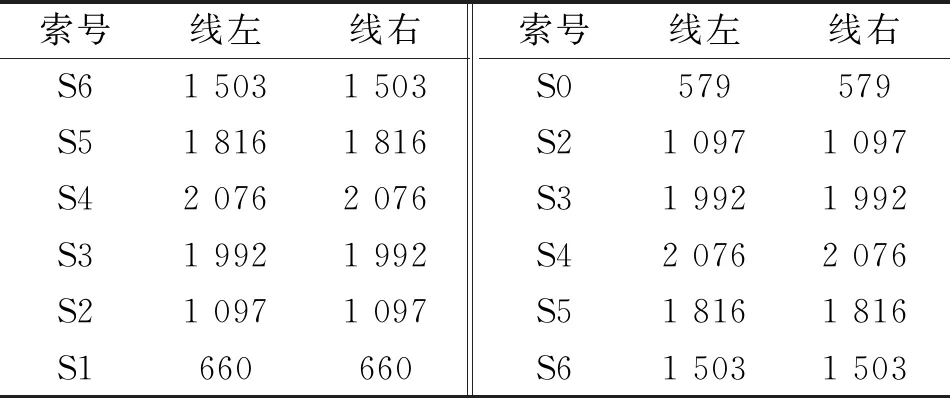
表2 对称的索力调整值 kN
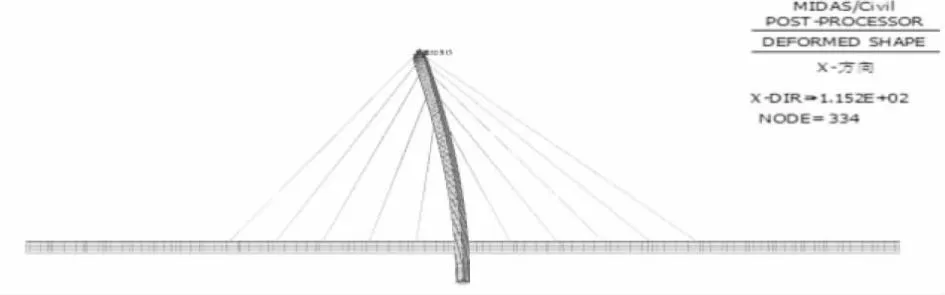
图6 施加对称调整值后的模型(单位:mm)
2.4 不对称二次调索计算
斜拉索初张拉后本桥主梁标高测量值较低,考虑本桥的钢主梁较柔,钢锚箱处的锚固垫板较厚,张拉损失较大,为了提高主梁高度,根据施工经验以初张拉索力设计值增大5%为目标索力进行不对称二次调索,不仅可以提高主梁高度,而且不会对斜拉索索力有太大影响。基于一个模拟现场桥塔初张拉偏位现状的模型,按照S6→S0的张拉顺序分批次张拉斜拉索,采用迭代法计算得到斜拉索索力调整值见表3。可以发现斜拉索索力调整值并不对称,相当一部分斜拉索存在超张拉情况,不过并未超出安全范围。

表3 增大5%索力设计值迭代计算 kN
2.5 不对称二次调索结果
按照索力和线形双控,采用不对称的索力调整值进行二次调索后,斜拉索索力结果见表4和图7(以线左为例),线形结果见图8,桥塔偏位情况如图9。在每根索张拉过程中动态监测对应拉索的标高,二次张拉完成后对全桥索力和线形进行复测。

表4 二次调索索力对比

图7 二次调索后索力对比
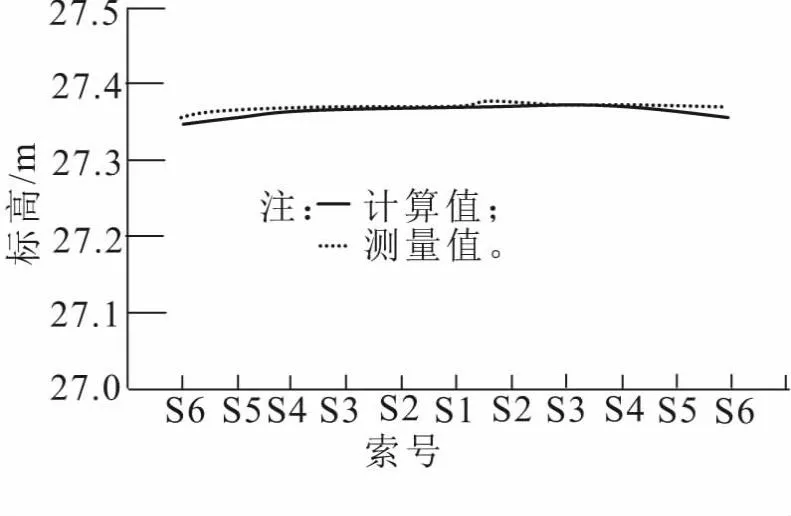
图8 二次调索后梁中线线形
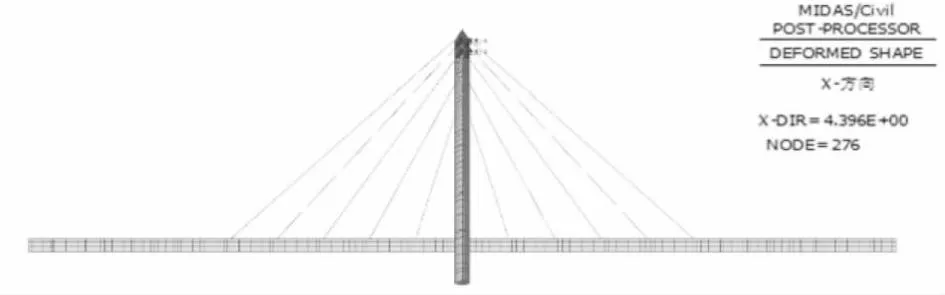
图9 不对称调索后桥塔偏位情况(单位:mm)
由此可知,通过不对称调索技术进行二次调索后,斜拉索的索力及主梁线形与计算值十分相近,误差控制在2%及以内。钢拱桥轴线顺桥向倾斜偏位最大4.396 mm,控制在了20 mm以内,结构受力对称、合理。柔性拱塔不对称调索技术成功应用,该斜拉桥索力及线形处于较合理的状态,保证了后续施工及运营的安全。
3 结论
(1)通过建立有限元模型进行施工过程的模拟,利用迭代法能够高效地得到各个施工阶段的设计索力及成桥合理索力。张拉结束的索力与设计索力相差在5%以内可认为完成调索。
(2)施工过程中按照索力及线形两个标准把控,以线形控制为主、索力控制为辅,可以准确了解各施工阶段主梁及斜拉索的受力状态,能够起到更好的监控作用,保证工程质量。
(3)柔性桥塔易受施工过程中不对称临时约束等条件的影响,导致桥塔受到不对称的索力进而向一侧偏位。通过迭代法得到一组合理的不对称的索力调整值,按照一定的调索顺序进行二次调索,能够使得斜拉索索力对称,消除桥塔偏位。
