动力学系统在亏损时的反馈控制设计

任万灿,陈慧琴,王立才

(北华大学机械工程学院,吉林 吉林 132013)

许多学者已经对非亏损振动系统反馈控制器设计方法进行了大量理论研究[1-5]。MEIROVITCH L[6]给出了振动系统反馈的标准设计方法;刘中生等[7]研究了重频系统模态的可控制性与可观性,但没有考虑控制的设计问题。已有研究中的动力学系统是非亏损的,即具有完备的特征向量系。而一些实际工程问题(如气动弹性颤振、受不确定载荷影响的桥梁颤振、结构与控制中的耦合等)在一定条件下会发生亏损现象[8],这类系统称为亏损系统,即不存在完备的特征向量组来张成整个特征空间,在这种情况下,针对非亏损系统反馈控制器设计的方法将失效[9]。CHEN等[10]介绍了亏损和接近亏损系统的模态优化控制问题;陈宇东等[11]给出了亏损系统振动模态的可控、可观性量度指标;李有意[12]研究了非亏损振动系统模态控制器的设计方法,但其计算过程比较复杂;WANG等[13]讨论了非线性亏损系统在Hopf分叉临界点的反馈控制,但并未给出反馈控制器设计方法。上述反馈控制都局限于非亏损系统,因此,有必要给出系统亏损时的反馈控制器设计方法。本文主要研究动力学亏损系统模态反馈控制器的设计问题,给出相应反馈控制器模态向量的计算方法,并通过二自由度机翼的反馈控制,验证该方法的有效性。

1 广义模态坐标下动力学系统的反馈控制

一般动力学系统的微分方程和控制方程分别为

(1)

和

(2)

式中:矩阵M、C和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;q∈n为位移向量;b0∈n为控制向量;z(t)∈为控制输入。

利用状态变换,系统(1)的状态方程和控制方程(2)可表达为

和

(3)

其中:

(4)

x(t)∈2n为状态向量;z(t)∈为控制输入;A∈2n×2n为系统状态矩阵;b∈2n为控制向量;G∈2n为状态反馈增益向量。

对于系统(3)中的矩阵A,由高等代数可知,存在可逆右广义模态矩阵V使式(5)成立

AV=VJ,

(5)

其中:矩阵J为状态矩阵A的Jordan标准型,可表示为

设状态矩阵A的左广义模态矩阵为U,满足关系式(6),

AHU=UJH,

(6)

式中:矩阵AH和JH分别为矩阵A和J的共轭转置。可证明,左、右广义模态矩阵U、V满足双正交条件[14]

UHAV=J,UHV=I,

(7)

式中:矩阵UH为U的共轭转置矩阵;I为2n阶单位阵。

引入线性反馈增益向量GT形成控制输入z(t),闭环系统的动态特性将发生相应变化。可设计一个新的闭环系统,使得亏损系统状态矩阵的特征值被重新指定为新的孤立特征值。相比原来未控制系统(1),具有更好的运动特性。

利用右广义模态变换

x(t)=Vξ(t) ,

(8)

其中:ξ(t)为广义模态坐标向量。振动控制方程(3)可转化为广义模态坐标下的控制方程

(9)

式中:

H=J+pgT,p=UHb=[p1,p2,…,p2n]T,gT=GTV=[g1,g2,…,g2n] 。

(10)

2 系统状态矩阵具有单个Jordan块的模态控制器设计

若系统(3)状态矩阵A的Jordan标准型J为单个Jordan块,设λ为A的2n重特征值,具体形式为

矩阵J为非对角阵,则系统(3)为亏损系统。

系统(3)在广义模态坐标下的控制方程如式(9)所示。

设新指定的孤立特征值为ρj(j=1,2,…,2n),其相应的模态向量为ωj,并满足关系式(11):

(J+pgT)ωj=ρjωj,j=1,2,…,2n。

(11)

因为ωj≠0,则

det(J+pgT-ρjI)=0 。

(12)

由式(9)可张成矩阵pgT,并将其代入式(12)得

(13)

根据式(13)行列式结构,采用添零升阶法[15]来简化计算

(14)

式(14)经过行变换可化为

(15)

将式(15)继续进行行变换,将副对角线的元素“1”全部变为“0”,得到

(16)

式中:

(17)

利用对角线元素消去式(16)中K1、K2、…、K2n,得到

即行列式结果为

(18)

由迭代关系式(17),式(18)可进一步化简为

(19)

假定λ≠ρj,式(19)化为

(20)

式(20)可写成简洁的矩阵形式

FPg=E,

(21)

式中:

由式(21)可得

g=P-1F-1E。

(22)

根据式(10)得到闭环系统状态反馈增益向量

GT=gTUH。

(23)

将式(22)代入式(23)得到闭环系统状态反馈增益向量

GT=ET(F-1)T(P-1)TUH。

3 具有多个Jordan块的模态控制器设计

3.1 系统状态矩阵具有两个Jordan块的模态控制器设计

若系统(3)状态矩阵A的Jordan标准型J可表示为两个Jordan块的直和,即J=J(1)⊕J(2)。设λ1、λ2为A的两个不同特征值且对应代数重数分别为m和2n-m,可将其Jordan标准型J表示为分块形式

其中:

状态矩阵A的左、右模态矩阵U、V同样进行分块处理,即

U=[U(1)U(2)] ,V=[V(1)V(2)] 。

(24)

左、右广义模态矩阵U、V的各个分块矩阵U(j)、V(j)(j=1,2)具体为

(25)

(26)

式(24)、(25)和(26)满足双正交条件式(7),利用右广义模态变换式(8)可得

其中:ξ(t)为广义模态坐标向量,则振动控制方程(3)可转化为如下的模态控制方程

(27)

其中:

(28)

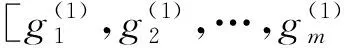
设式(27)的特征值为ρj(j=1,2,…,2n),其相应的模态为ωj,并满足关系式(29):

(J+b1gT)ωj=ρjωj,j=1,2,…,2n。

(29)

因为ωj≠0,则

det(J+b1gT-ρjI)=0 。

(30)

(31)

利用化简式(13)的方法对式(31)进行同样处理,得

(32)

对式(32)进行行初等变换

(33)

将式(33)继续进行行变换,将副对角线的元素“1”全部变为“0”,得到

(34)

式中:

(35)

利用对角线元素消去式(34)中B1、B2、…、Bm,C1、C2、…、C2n-m,得到

此行列式值为

(36)

由递推关系(35)进一步简化式(36),得

(37)

假定λ1≠ρj,λ2≠ρj,式(37)化为

(38)

式(38)可写成简洁的矩阵形式

FPg=E,

(39)

其中:

(40)

(41)

(42)

由式(39)可得

g=P-1F-1E。

(43)

根据式(28)得到闭环系统状态反馈增益向量

GT=gTUH。

(44)

将式(43)代入式(44),得到闭环系统状态反馈增益向量

GT=ET(F-1)T(P-1)TUH。

3.2 系统状态矩阵具有一般形式时的模态控制器设计

若系统(3)状态矩阵A的Jordan标准型J可表示为多个Jordan块的直和,即J=J(1)⊕J(2)⊕…⊕J(v),设λi(i=1,2,…,v)为A的v个不同特征值且对应代数重数为mi(i=1,2,…,v),则可将其Jordan标准型J表示为分块形式

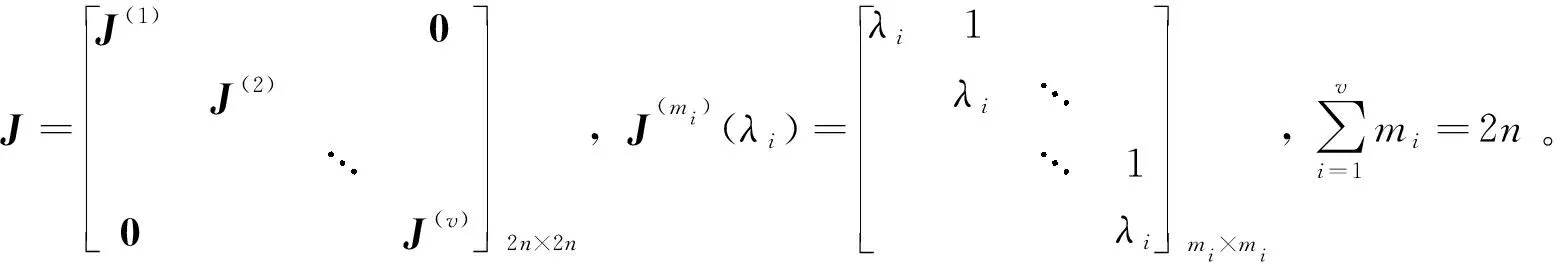
状态矩阵A的左、右模态矩阵U、V同样进行分块处理,即

U=[U(1)U(2)…U(v)] ,V=[V(1)V(2)…V(v)] 。

(45)

左、右广义模态矩阵U、V的各个分块矩阵U(i)、V(i)(i=1,2,…,v)具体如下:

(46)

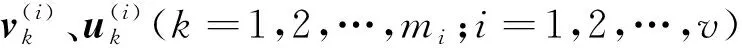
式(45)、(46)满足双正交条件式(7),振动控制方程(3)可转化为如下的模态控制方程

其中:

gT=GT[V(1)V(2)…V(v)]=[(g(1))T(g(2))T… (g(v))T],

(47)

此时系统的反馈增益向量计算方法与具有两个Jordan块相似,即与式(43)相似,其增益向量的解同样为

g=P-1F-1E,

(48)

其中:

4 数值算例

在航空工业领域,机翼(叶片)的颤振(系统发生亏损时)是航空飞行器失事的主要原因之一。为了减少事故,目前抑制和延缓亏损现象发生的最有效方法是前期恰当的结构控制设计。为了研究机翼颤振,建立二元机翼颤振模型[16]。机翼颤振时弯曲和扭转变形可等效为由垂直方向弯曲弹簧的位移和扭转弹簧绕刚度中心的旋转位移。将机翼简化为矩形截面梁,见图1。其中:机翼弦长为2b(b为半弦长);Kh和Kα分别为升降和俯仰的结构刚度系数;V为空速;M为刚度中心;ab为半弦点到刚度中心的距离;h为机翼刚度中心的垂直距离;α为机翼的俯仰角。

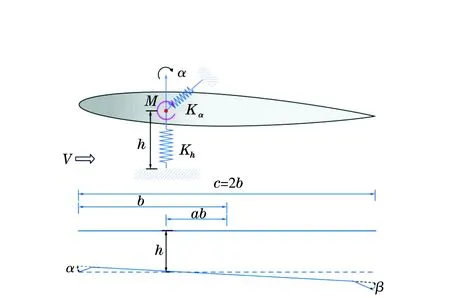
图1 二元机翼模型Fig.1 Model of two-dimensional airfoil

机翼振动方程可写为[8]

式中:m为机翼质量;s为质量静矩;Jα为质量惯矩;ε(0<ε≪1)为小参数;Q1、Q2分别为气动力和气动力矩。将运动方程写成矩阵形式

式中:M为质量矩阵;K为刚度矩阵;H为非对称的空气动力学矩阵;q为位移向量。分别具有以下形式

利用状态变换,机翼非线性运动方程及其线性部分可表示为

和

(49)

式中:

取参数s/m=0.25,Jα/m=Kα/m=0.5,Kh/m=0.25,ρab2/m=0.2,e=0.4,p2=v2/b,p=1.325 677 35,系统矩阵可具体表示为

此时系统状态矩阵特征值为

λ1=λ2=0.673 189j,λ3=λ4=-0.673 189j 。

矩阵A的Jordan标准型为

该Jordan标准型不能最简化为对角阵,则此系统是亏损的。因为Re(λ)=0,Im(λ)≠0,由微分方程稳定性理论可知,此时系统处于Hopf分叉临界状态(即机翼发生颤振)。

状态矩阵A的左右广义模态矩阵U、V分别为[14]

此系统处于Hopf分叉临界状态,需要引入反馈控制使其渐进稳定。多尺度法求解非线性微分方程可获得精度较高的解,既能计算严格的周期运动,还适用耗散系统的衰减振动和非稳态过程[17]。机翼的运动方程(49)及其控制方程[13]含有小参数ε,在多尺度分析中,通过将问题分解为不同尺度上的子问题,可以针对每个子问题建立相应的微分方程,通过解这些微分方程,可以获得精确的近似解。

利用多尺度法,系统(49)的零阶和一阶近似控制微分方程如下[13]:

对机翼垂直位移h进行反馈控制,由式(4)可知,控制输入为

则零阶控制方程具体形式为

(50)

由式(28)可知,

对振动控制方程(50)进行右模态变换:

其中:ξ0(t)为广义模态坐标向量。振动控制方程(50)可转化为如下的模态控制方程

(51)

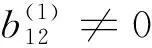
下面通过本文反馈控制器设计方法对系统进行闭环极点配置。先指定特征值

ρ1=-1+0.673 188 87j,ρ2=-1.2+0.673 188 87j,

ρ3=-1-0.673 188 87j,ρ4=-1.2-0.673 188 87j 。

由式(40)、(41)和(42)可得

得到增益向量的零阶近似修正g0:

计算输入z:

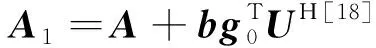
容易求出新的系统状态矩阵A1特征值

ρ1=-1+0.673 188 87j,ρ2=-1.2+0.673 188 87j,

ρ3=-1-0.673 188 87j,ρ4=-1.2-0.673 188 87j 。

综上,通过极点配置,控制系统得到了预期指定的特征值,达到渐进稳定。

5 小 结

本文基于广义模态理论,利用状态反馈控制和闭环控制系统的极点配置法,提出了一种计算反馈增益向量的新方法。该方法适用于状态矩阵具多个Jordan块的亏损系统,并且避免了繁杂的数学计算,使结果更为直观,易在计算机上实施,大大缩短了计算时间。由算例可知,动力学系统经过反馈控制,其特征值符合配置要求,系统达到渐进稳定。结果表明,此反馈增益向量的计算方法在振动系统为亏损时是有效的,适合工程应用。