用四点插值细分曲线拟合离散点列

邱 慧,李亚娟,邓重阳

(杭州电子科技大学,浙江 杭州 310018)

0 引 言

数据拟合广泛地应用于计算机辅助几何设计、计算机图形学[1]、逆向工程[2]等领域。B样条曲线以其分段光滑、几何不变性和局部支撑性等[3]优点成为了数据拟合的首选方法[4]。利用B样条曲线进行数据拟合时,通常需要先确定节点向量和参数,然后求解控制顶点。在节点向量和参数确定之后,控制顶点的计算即求解一个线性方程组[5]。而一般情况下,由于数据点的数量较多,所以经常需要采用迭代法计算该线性方程组。Lin等[6]提出了基于渐进迭代逼近(progressive and iterative approximation, PIA)的B样条曲线插值算法。2005年,赵宇等[7]对用于数据插值的PIA算法进行扩展,使该算法适用于数据逼近问题。而Deng等[8]进一步提出基于最小二乘法的渐进迭代逼近(progressive and iterative approximation for least squares, LSPIA)算法。该算法通过调整控制点的数目和节点向量构造一系列逼近数据点列的三次均匀B样条曲线。对于大规模的数据点集,在拟合过程中,也能够合理地控制拟合曲线的形状,具有保形的效果。近40年来,细分逐渐走入了计算机辅助几何设计、计算机图形学的研究领域。以其固有的特性,也被应用到曲线重建中[9]。细分法最早由Rham[10]提出,该方法几何直观,操作简单,修正方便,层次清晰,并且生成的曲线光滑性较好[11]。之后,Dyn等[12]提出的四点插值细分法是第一个单参数的插值型细分曲线造型法,且其极限曲线C1连续。本文利用Deng等[13]提出的四点插值细分法的极限曲线上的点的计算公式,结合离散点的参数化及最小二乘法(LSM)求解拟合曲线的初始控制点,并根据初始控制点确定逼近离散数据点列的四点插值细分曲线。与三次均匀B样条曲线的拟合算法相比,该算法在一定的拟合误差下,所需的初始控制点数目较少。在实际应用中,该算法只需少量的初始控制点即可确定离散数据点列的拟合曲线,具有数据简化的作用。而运用于多分辨率分析时,可以利用细分法的特性,控制初始控制点的细分次数,得到任意个数点列构成的拟合曲线。

1 四点插值细分法的极限曲线上的点的计算公式

四点插值细分法是细分法中的一个经典方法,根据其细分规则递归地定义极限曲线。

(1)

图1 以初始控制点细分多次形成的四点插值细分极限曲线

四点插值细分法虽然是单参数的插值型细分法,但由于细分规则的非参数化表达,这使其在应用中受到了很多限制。所以在应用中,通过借助四点插值细分法的极限曲线上的点的计算公式,由参数值直接确定每一个离散点对应在极限曲线上的确切位置。同时,这也有利于之后将本文算法推广到曲面的工作。

(2)

同理,极限曲线上的任一极限点都可由初始控制点表示其在极限曲线上的精确位置。

2 基于四点插值细分法多项式表示曲线拟合算法

相比于参数形式和隐函数形式表示的曲线造型方法,细分法具有参数法的许多优点[14]。而四点插值细分法不仅细分规则及表示相对较简单,而且具有多项式重构性,应用于拟合离散数据点列,将比参数法具有更强的适应性。

本节将详细介绍基于四点插值细分法多项式表示的曲线拟合算法,并给出其实现步骤。

2.1 算法描述

2.1.1 一般参数化确定系数点列

(3)

[Pk+1]=Ak[Pk]

(4)

[Pk]=A[P0]

(5)

(6)

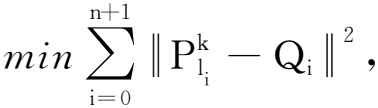
2.1.2 分组参数化确定系数矩阵

对每一个t′i,i=1,…,n+1,可由

(7)

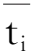
(8)

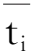
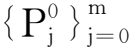
(9)

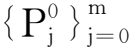
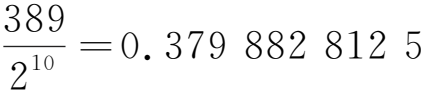
相比于公式,公式的计算方法简单方便,且可达到算法的要求。

本文算法步骤如下:

3 实例与分析

本节通过三个具体实例,展示了四点插值细分曲线拟合算法的拟合效果。并将其拟合效果与三次均匀B样条曲线的拟合效果,分别就给定拟合误差下的控制顶点数目和给定控制顶点数目下的拟合误差进行对比。实验数据说明该算法在实际应用中能够对数据点列进行有效拟合。

本节利用LSPIA算法构造三次均匀B样条曲线。另外,选用距离平方和的均值作为拟合误差,其计算公式为:

(10)

以下三个实例中,离散数据点列都提取于一些封闭图像模型的边框轮廓,具有随机性和代表性。图2～图4中,图(a)及图(c)内的圆点表示细分的初始控制点,图(b)中的圆点表示细分一次后所产生的新点及老点,图5～图7中的圆点均表示细分的初始控制点。

图2～图4分别为由70、40、40个初始控制点细分多次形成的四点插值细分曲线拟合离散数据点列。其中,(d)图的拟合曲线是以LSPIA算法构造的一系列三次均匀B样条曲线。初始控制点与对应例子个数相同,并且在前后两次迭代的拟合误差相差10-7时算法停止迭代。

图2 例1:四点插值细分曲线与三次均匀B样条曲线拟合1161个离散数据点列所形成的近似曲线

图3 例2:四点插值细分曲线与三次均匀B样条曲线拟合501个离散数据点列所形成的近似曲线

图4 例3:四点插值细分曲线与三次均匀B样条曲线拟合577个离散数据点列所形成的近似曲线

上述实例在控制点个数相同下,不同算法的拟合误差对比如表1所示。由表可知,利用四点插值细分法拟合离散点列,其拟合误差相比之下更小。其中EB-spline表示由LSPIA算法构造的一系列三次均匀B样条曲线的拟合误差,E4-point表示由本文算法构造的四点插值细分曲线的拟合误差。

表1 控制点个数相同时,不同算法的拟合误差

而由表2可知在给定的拟合误差下,本文算法利用的初始控制点数目较少,其中PB-spline表示由LSPIA算法构造的一系列三次均匀B样条曲线的初始控制点个数,P4-point表示由本文算法构造的四点插值细分曲线的初始控制点个数。

表2 拟合误差相同时,不同算法的初始控制点个数

图5～图7为对应实例依次新增10个初始控制顶点时,曲线拟合离散数据点列的情况。

图5 例1 不同初始控制点的四点插值细分曲线拟合离散数据点列所形成的近似曲线

图6 例2:不同初始控制点的四点插值细分曲线拟合离散数据点列所形成的近似曲线

图7 例3:不同初始控制点的四点插值细分曲线拟合离散数据点列所形成的近似曲线

初始控制点依次递增10个,三个实例对应的曲线拟合误差如表3所示,其中N0表示每个实例首次拟合的初始控制点个数,即在实例1中,N0=70,而在实例2、3中,N0=40,在此基础上,每次拟合的初始控制点依次递增10个,但对应的拟合误差都逐渐减少。

表3 依次递增10个初始控制点时,不同实例的拟合误差

当处理数据点集时,该算法可以充分利用细分法的特性,以少量的初始控制点得到数据点列中任意多个有效的近似数据点,进行数据分析。例如上文的第1个例子,算法将70个初始控制点细分1次、2次,直至多次,分别得到140个数据点、280个数据点、拟合所有离散数据点列的曲线。这样可以在不同的研究目的下,选择不同个数的数据集,减少研究的工作量,提高工作效率。另外,在存储数据点列时,只需存储少量的初始控制点,即可得到与原数据点列误差较小的近似数据点列,节约数据点列的存储空间。

4 结束语

本文提出一种用四点插值细分曲线拟合离散点列的算法。该算法适用于拟合散乱数据点集,与三次均匀B样条曲线的拟合算法相比,在一定的拟合误差下,可以有效减少拟合曲线的初始控制点的个数。在实际应用中,利用该算法可以有效地对曲线模型的数据点列进行简化,提高工作效率。另外,该算法运用于多分辨率分析时,可以得到由任意个数点构成的拟合曲线。下一步将该算法推广到曲面的情况。