基于数值模拟的工程设计中参数不确定性表征方法研究综述

熊芬芬，李泽贤，刘宇，夏侯唐凡

1.北京理工大学 宇航学院，北京 100081

2.电子科技大学 机械与电气工程学院，成都 611731

为了缩短设计周期、降低开发成本、满足产品不断提升的性能需求和更新换代频次，计算流体力学（Computational Fluid Dynamics，CFD）、结构有限元分析（Finite Element Analysis，FEA）等数值模拟技术正在成为科学研究和工程设计等许多领域内解决问题的主流方法［1］。在航空航天领域，CFD 和FEA 已分别成为气动和结构分析设计中不可或缺的研究手段。《中国制造2025》指出，仿真技术对于发展和提高中国制造能力具有重要支撑作用，特别是2015 年12 月31 号国家出台了智能制造标准体系建设指南，其中明确了要在制造生产过程中应用仿真技术［2］。

飞行器等复杂装备的整个寿命周期都充满了源于仿真建模和模拟、生产制造（如几何尺寸）、工作环境（如载荷环境）、仪器监测（如测量误差和信息处理）等的大量不确定性［3］。一般而言，根据不确定性属性的不同，可以将不确定性分为随机不确定性（Aleatory Uncertainty）、认知不确定性（Epistemic Uncertainty）或者是两者兼而有之的混合不确定性［4］。其中，随机不确定性源于物理现象中存在的固有随机性，无法通过收集更多信息进行控制或减小；认知不确定性源于知识的缺乏、数据的不足，可通过知识增加、建模方法改进、数据搜集等达到减小甚至消除的目的。不确定性按照来源又可分为参数不确定性、模型不确定性和数据不确定性［5］。对于数值模拟，以广泛用于飞行器空气动力计算的CFD 仿真为例，不确定性一般可归为模型形式不确定性、模型参数不确定性和模型数值离散不确定性［6］。模型形式不确定性属于认知不确定性，一方面源于求解湍流流场时湍流模型的选择，采用不同的假设构造的湍流模型会对数值模拟结果有较大影响［7］；另一方面源于数值模拟建模所作的各种假设和简化，使得仿真结果与试验数据存在偏差。模型参数不确定性既包含攻角、雷诺数、压力、流量等来流和边界条件和制造误差、工艺波动等影响几何尺寸的随机不确定性，也包含湍流模型封闭系数以及卡门数、壁面普朗特数等认知不确定性［8］。对这些不确定性进行表征时，由于数据匮乏会导致数据不确定性，这属于认知不确定性。模型数值离散不确定性也属于认知不确定性，其源于对控制方程及边界条件离散化造成的截断误差和迭代误差［9］。

一方面，这些不确定性必然会导致数值仿真的输出响应也存在不可忽视的不确定性，且输出极有可能对某些不确定性非常敏感，例如激波在翼型上表面的位置和激波后压力对湍流模型封闭系数的变化非常敏感［10］，严重影响CFD 结果的可信度，这对于具有高可靠性要求的航空航天装备而言，极有可能引入潜在风险，因此开展优化设计前必须对数值模拟进行模型确认（Model Validation）。另一方面，这些不确定性必然会导致飞行器系统性能的波动，甚至导致设计失效，带来灾难性后果。例如NASA 的高超声速飞行器X43-A 试验失败，究其原因是对气动设计不确定性因素模拟不足［11］。因此，需要在飞行器等复杂装备设计中开展不确定性下的优化设计（Design Optimization under Uncertainty），如稳健优化设计［12-13］和基于可靠性的优化设计［14-15］，提升系统性能的同时确保系统的稳健和可靠。对数值模拟模型确认和不确定性下的优化设计，其关键皆为不确定性量化（Uncertainty Quantification，UQ），主要包括不确定性表征（Uncertainty Characterization）和不确定性传播（Uncertainty Propagation，UP）2 个关键部分。图1 对基于概率理论的UQ 进行了示意。

图1 基于概率理论的不确定性量化示意Fig.1 Schematic of uncertainty quantification based on probability theory

如图1 所示，不确定性表征是根据不确定性变量的数据（源于测量、理论或专家等）建立数学模型的过程，具体指：①指定不确定性的数学结构；②确定结构所需元素的数值。比如，随机变量可建模为概率分布模型（见图中随机变量x1、x2、x3的实线概率密度曲线）。不确定性传播包含正向和反向不确定性传播，正向UP 研究在输入不确定性的影响下，系统输出（通常也称为感兴趣的量Quantity of Interest，QoI）的不确定性（图1 中实线表示从输入x=［x1，x2，x3］到输出y的不确定性传播过程）；反向UP 研究根据y的观测数据反向推理计算输入不确定性（图1 中虚线从输出y反推输入x的不确定性传播过程），最终得到图中随机变量x1、x2、x3的虚线概率密度曲线，需在正向UP 的基础上进行［16］。当然，不确定性表征不仅可以用于输入不确定性变量，还可直接应用于系统的QoI。例如，对于CFD 数值模拟可以基于湍流模型系数、来流等不确定性表征的结果，进行正向UP 得到流场压力场的不确定性，也可根据压力场的测量数据，直接对其进行不确定性表征建模。此外，根据流场压力场的测量数据，可利用反向UP 对湍流模型系数的不确定性表征模型进行修正。本文后续提及UP，若不作特殊说明皆指正向UP。基于QoI 不确定性量化的结果，可进行设计和决策，比如确定是否接受或有多大信心接受当前的数值仿真模型或设计方案。显然，对不确定性进行合理的表征建模至关重要［17-18］，它是实施UQ 的前提。

在对数值模拟模型形式不确定性的研究中，当考虑单个数值模拟模型时，基于该模型进行不确定性传播。比如，CFD 中考虑湍流模型系数或雷诺应力的不确定性，比较UQ 结果与试验数据来估计模型形式不确定度，形成了模型评价的假设检验统计量、贝叶斯因子、频率指标、面积度量等诸多模型确认度量指标［19］；当考虑多个数值模拟模型时，通过模型选择或数据融合的方式对模型预测中的模型选择不确定性进行量化，其中贝叶斯模型平均（Bayesian Model Averaging，BMA）是目前较为常用的方法。Chen 等［20］针对机械系统的疲劳裂纹问题，基于BMA 方法量化了模拟性能退化的维纳过程模型、伽马过程模型和逆高斯过程模型所引入的模型形式不确定性。Tang 等［21］基于证据理论对ZAERO 和NASTRAN 软件所模拟的导弹舵面颤振仿真结果进行了融合，从数据融合的角度进行了模型形式（不同仿真平台）的不确定性量化。由此可见，模型形式不确定性量化最终都归结到单个模型的参数不确定性表征及传播。

数值模拟中数值离散的不确定性主要指离散误差的估计，Richardson 外推是较为常用的估计方法，它将数值离散不确定性表征为一个认知不确定性区间。Schaefer 等［5］基于Richardson 外推对NASA 提出的通用运输机研究模型（CRM）的网格收敛误差进行了估计，得到了其升阻力系数的认知不确定性区间。陈江涛等［22］同时考虑了数值离散不确定性和模型形式不确定性，提出了一种考虑数值离散误差的湍流模型选择不确定度量化方法，基于Richardson 外推计算了SA湍流模型和湍流k-ω模型真解的95%置信区间，然后将其作为认知不确定性通过二阶概率框架给出了NACA0012 低速绕流和CHN-T1 跨声速绕流中升阻力系数的概率分布上下限。对于基于数值模拟的工程设计，狭义上讲，不确定性表征都可以归为对参数的不确定性表征。因此本文主要综述各种参数不确定性表征方法，以下提及的不确定性表征皆指参数不确定性表征。

目前关于不确定性传播，国内外学者从不同角度开展了大量研究以及综述性工作。在随机不确定性传播方面，产生了蒙特卡洛模拟［23］、混沌多项式［24］、随机配点［25］、高斯数值积分［26］、多可信度不确定性传播［27］等诸多方法，并应用在飞行器气动系数［28］、火箭气动载荷［29］、结构形变［30］、电阻抗成像［31］、CFD 数值模拟［32］等大量不确定度量化问题中。在认知不确定性传播方面，产生了基于区间、概率盒（Probability-Box，p-box）、D-S（Dempster-Shafer）证据、模糊、可能性、粗糙集等理论的方法［33］，分别应用于飞机结构［34］、翼型气动特性［35］、屋顶结构形变特性［36］等诸多不确定度量化问题。关于混合不确定性传播，大多将概率理论与区间分析、概率盒、模糊集、证据理论等其中一种认知不确定性量化方法相结合，形成外层处理认知不确定性、内层处理随机不确定性的双层嵌套抽样混合不确定性传播框架［37］。这些研究在进行不确定性传播时，均假设不确定输入数学模型已知，如正态、均匀分布或区间模型，例如气动力系数不确定性量化中将马赫数、迎角、箭体几何外形等直接假设建模为正态分布［28］、将湍流模型封闭系数建模为均匀分布［38］；气动弹性不确定性量化中将高超声速舵面热不确定性建模为正态分布［29］；结构不确定性量化中将杨氏模量、横截面积、外部载荷不确定性建模为对数正态分布和极值分布［30］。如此假设未必合理，由此得到的不确定度量化结果对工程问题的参考价值有限，需要根据具体场景下不确定性变量信息对其建立合理的数学表征模型。Ferson 等［39］对美国Sandia 实验室发起的认知不确定性研讨会进行总结，指出不确定性表征是值得进一步研究的关键。相比不确定性传播，不确定性表征方面的研究明显要少，鲜有综述性的研究工作报道。

本文面向基于数值模拟的工程设计，主要回顾国内外已经开展的不确定性表征工作，总结不确定性表征的基本内容和方法，并对表征后的不确定性传播的基本思路进行简要介绍，最后给出进一步开展不确定性表征研究的思考与建议。

1 不确定性表征概述

表征不确定性的信息来源主要包括：①真实或相似条件下的试验测量数据；②理论模型生成的数据；③专家意见。在这些信息来源下，可将表征不确定性的信息源分为3 类［4］：①强统计信息，具有大量试验或高可信理论数据，可足够确信地构建不确定性变量的概率统计模型；②稀疏统计信息，很多情况下仅具有不确定性变量的少量试验或高可信理论数据，无法构建确定的统计模型，否则构建的统计模型存在大量认知不确定性；③不精确信息，如专家判断存在一个或多个具有上下界的区间，这多个区间可能来自不同专家或团队。实际中，不确定变量的信息源往往是上述信息源的混合，比如某仪器的稀疏测量数据可能以区间形式存在，正态分布的均值可能位于某个区间。

不确定性表征需解决3 个关键问题，一是要从本质和来源上摸清不确定性的类型，包括随机不确定性、认知不确定性以及两者兼而有之的混合不确定性，这需要结合具体物理对象确定；二是要建立不确定性的数学模型，包括但不限于概率框架下的概率密度函数以及非概率框架下的广义区间表达等，通常这需要根据不确定性的信息源决定采取何种建模方法；三是要获取数学模型中的全部参数，如正态分布模型的均值、方差，或区间模型的上下界以及可信度等。

图2 总结了目前主流的不确定性表征方法，其中随机不确定性的概率表征方法发展相对较为成熟，但由于经典的概率建模和参数估计方法仅能处理不确定性源的信息形式为点数据且数据足够多的情况，具有一定局限性。针对随机不确定性以稀疏点数据和/或区间数据、区间数据形式存在的情况，也可认为由于数据不足而导致的认知不确定性，目前产生了处理稀疏点和/或区间数据的基于似然理论的表征方法［40］、概率分布混合加权的表征方法［41］、专门处理区间数据的概率表征方法［42］。对于认知不确定性表征，目前方法较多且研究较为独立，其共同之处是无法直接根据不确定性源的信息形式进行建模，通常需要专家信息，比如证据理论需要给定不确定性变量的证据结构，模糊理论需要给定隶属度函数。

图2 不确定性表征方法Fig.2 Uncertainty characterization methods

表1 对不确定性表征方法的特点进行了分类整理，不失一般性，按照概率和非概率方法两大类展开。概率表征方法均以经典概率统计为理论基础，将不确定性变量建模为概率分布，其最大优势是可便捷地应用于各类基于概率的不确定性传播和优化设计理论和方法。非概率表征方法由于涉及新的理论体系，对于后续的不确定性传播和设计，可能需要花费更多的精力进行人员培训［43］。一些学者认为纯概率方法可完全考虑各种形式的不确定性，但更多学者认为非概率表征方法在认知不确定性处理上更加合理［39］。根据表征不确定性的信息源所属类别，可对不确定性进行分类，在此基础上再进行表征，为此第3 节介绍了一种考虑随机、稀疏和区间变量的不确定性分类准则及相应的不确定性建模方法。

表1 各种不确定性表征方法的特点Table 1 Characteristics of various uncertainty characterization methods

根据概率表征和非概率表征框架，第2 节介绍了经典的概率表征方法，第3、4、5 节则按照表征不确定性的不同信息源形式，分别介绍了处理点数据、稀疏点数据和/或区间数据、区间数据的不确定性表征方法。第6 节针对场变量介绍了常用的随机场表征方法。第7 节介绍了处理认知不确定性的非概率表征方法。

2 基于经典概率统计的表征方法

概率统计法具有成熟的理论基础，保证了它在处理随机不确定性时的有效性。如果信息足够估计变量的概率分布，则可通过经典概率统计法将随机不确定性建模为随机变量。这种随机不确定性的概率分布表征方法目前已经在结构优化［44］、气动分析［45-46］、电工电子［47］、核工业技术［48］、水利水电［49-50］、航空航天［51-52］等诸多领域得到广泛应用。

2.1 参数估计

首先，根据经验、先验知识或专家意见，以及变量的不确定性特征及其所涉及的物理背景，确定随机变量服从的分布（如均匀、高斯、泊松、对数正态等）。然后，基于试验观测数据或其他可用信息，采用矩估计（Moment Estimation）［53］、极大似然估计（Maximum Likelihood Estimation，MLE）［54］、贝叶斯估计（Bayesian Estimation）和最大后验（Maximum A Posteriori，MAP）估计［55］等参数估计方法求得分布的参数（如正态分布的均值和标准差）。基于经典概率统计的不确定性表征方法最终都能根据点数据得到不确定性变量的概率分布。

张文生等［56］针对土质边坡可靠度分析，将岩土参数中黏聚力和内摩擦角随机变量表征为正态分布，利用矩估计方法估计了分布的均值和方差。Kim 等［57］针对悬臂梁挠度测量误差的不确定性，采用极大似然估计方法估计假设的均匀分布和正态分布的分布参数，为考虑测量误差时的观测数据的不确定性表征提供了指导。张诺亚［58］基于贝叶斯估计获得了煤矿地下电性分布模型，并开展了模型参数的不确性分析和可靠度评估。Edeling 等［59］在二维分离流和三维可压缩流等高雷诺数流动问题计算中，采用最大后验估计对CFD 仿真中使用的k-ε、k-ω、SA 湍流模型封闭系数进行了估计，以量化湍流模型的不确定性。

本节主要介绍最为常用的极大似然估计和贝叶斯估计。

2.1.1 极大似然估计

极大似然估计是一种利用已知的样本信息反推最具有可能（最大概率）导致这些样本结果出现的概率模型分布参数的估计方法，即“分布已定，参数未知”。对于连续型概率分布f(x；θ)，其中x为随机变量，θ为未知参数。从总体X中取出样本容量为n的简单样本和其样本观测值分别为(X1，X2，…，Xn)和(x1，x2，…，xn)，则样本的似然函数（即联合概率密度）为

极大似然估计就是给定样本观测值(x1，x2，…，xn)下，选取未知参数θ的估计值使得似然函数最大的过程。在样本数量较大的情况下，概率连乘会导致数据下溢，产生较大数值计算误差，由于似然函数及其对数函数在同一点处达到最大，通常对似然函数取对数进行求解。

极大似然估计基于经典概率统计理论，为获得准确的参数估计结果，文献［60］建议样本数据量大于30。实际中待估计参数维数不同，对数据量的要求也会有所不同［61］，但并未给出确切的参数维数和数据量间的定量关系。

2.1.2 贝叶斯估计

在数据量较少或比较稀疏的情况下，直接利用MLE 存在一定误差，此时可利用贝叶斯估计方法，认为待估计参数也服从某种概率分布，已有数据只是在这种参数的分布下所产生的。该方法也被认为是一种可处理数据不足而导致的认知不确定性的有效方法。

在样本观测值x=(x1，x2，…，xn)下，待估计参数θ的条件概率密度为

式中：π(θ)为参数θ的先验分布；f(x|θ)为总体X的条件分布；π(θ|x)为参数θ的后验分布；分子项f(x|θ)π(θ)为参数和样本的联合分布，分母项∫θ f(x|θ)π(θ)dθ为样本观测值x的边缘概率密度。

在贝叶斯估计中，若采用极大似然估计的思想，考虑后验分布极大化而求解θ，则变成了最大后验估计：

2.1.3 分布类型的选择

上述参数估计方法的应用前提是概率分布类型已指定，并未给出如何判定选择最为合适的分布类型的方法，实际中极有可能缺乏指定分布类型所需要的信息。此时，可基于不确定性变量的给定数据（观测或理论）应用拟合优度检验（Goodness of Fit，GOF）或模型选择方法来确定分布，给出接受或拒绝一个候选分布适合表示给定数据假设的结论。

最具代表性的拟合优度检验有Kolmogorov-Smirnov（K-S）、Anderson-Darling（A-D）和卡方（χ2）检验［62-64］。K-S 检验和A-D 检验均通过比较经验数据分布与候选分布的累积分布函数（Cumulative Distribution Function，CDF）间的距离，来度量2 个分布间的差异程度，但A-D 检验将权重应用于尾端概率分布，这对那些要求尾端概率分布较为精确的情况比较有用。χ2检验则是直接比较数据频率和候选分布的概率密度函数（Probability Density Function，PDF）之间的吻合程度。拟合优度检验为候选分布是否可表征给定数据提供了有效验证手段，但是识别出的正确分布模型通常有多个，无法对各个模型的优劣排序，尤其当样本数量较少时该问题广泛存在。

模型选择方法可有效解决上述问题，主要包括极大似然估计（MLE）、赤池信息准则（Akaike Information Criterion，AIC）、赤池信息修正准则（AICc）和贝叶斯信息准则（Bayesian Information Criterion，BIC））等［65-67］。其基本原理为：参考分布越接近不确定性变量的给定数据，对应的似然函数值越高，AIC 值、AICc 值和BIC 值的计算公式依次分别为

式中：Lmax为候选分布的似然函数最大值；k为候选分布的模型参数个数；n为样本量。

MLE 方法仅计算候选分布似然函数最大值的负对数-ln(Lmax)，通常认为三参数分布比一或二参数分布更适合，因此有时会错误地将三参数分布识别为正确分布。如式（4）所示，相比MLE，AIC 额外考虑了参数的数量，权衡估计模型复杂度和拟合数据优良性。

作为AIC 的修正版本，AICc 在信息损失计算中额外考虑了样本量n，适用于小样本下的模型选择。BIC 又进一步考虑了参数个数的影响，相较于AIC 和AICc，BIC 所引入的与模型参数个数相关的惩罚项kln(n)所占比重更大，当样本量较多时，可有效防止追求模型高精度所导致的模型复杂度过高。文献［65-67］对3 种准则及其惩罚项和修正项的引入给出了详细的理论推导。

Lim 等［68］采用AIC 准则建立了不确定变量的表征模型，对白车身及发动机车架进行了结构有限元仿真，开展了性能可靠度分析及基于可靠性的优化设计。Kang 等［69］比较了AIC、AICc 和BIC 3 种方法对多种概率分布类型识别的准确率，得出BIC 准则识别准确率最高。陈健等［70］在比较MLE、AIC 和BIC 时也得出了类似结论。此外，Kang 等还对K-S、A-D 和χ2检验在不确定性表征中的效果进行了比较，得出K-S 检验和A-D检验精度相当，但A-D 检验对于极值分布的识别正确率较低，而χ2检验在不确定性的样本数据量较小时检验结果并不准确，因此K-S 检验被认为是相对较好的拟合优度检验方法。

Kang 等［69，71］提出了一种结合拟合优度检验和模型选择的序列统计建模方法，首先通过拟合优度检验筛选掉不符合给定样本数据的候选分布，然后应用模型选择方法对接受的候选分布进行优劣排序。当拟合优度检验拒绝了全部可能的候选模型分布时，则利用核密度估计（Kernel Density Estimation，KDE）方法［72］获得不确定性变量的概率密度分布。图3［69］为Kang 等提出的序列统计建模方法的实施流程，图中N和Ntot分别表示候选模型数量以及全部可能的模型数量。

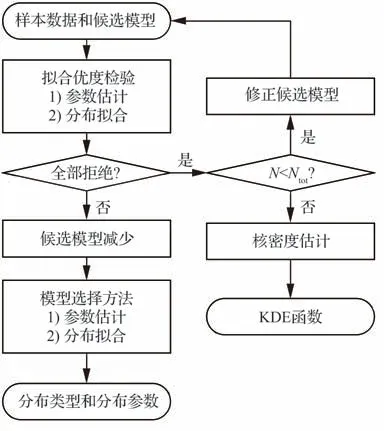
图3 序列统计建模方法［69］Fig.3 Sequential statistical modeling method［69］

Kang 等的研究表明，对于不同的分布类型和样本数目，K-S 检验和BIC 方法的组合可获得最高的估计精度。但是，由于拟合优度检验和模型选择方法都需在给定数据较充足的情况下才可精确识别分布类型，所以Kang 等提出的方法适用条件为n＞30。

2.2 非参数估计

参数估计需基于工程经验或专家意见等信息对概率分布进行假设，非参数法无需提前假设参数的概率分布，可直接根据数据特征进行分布拟合，避免对概率分布模型的假定不当导致重大错误。本节将介绍常用的基于最大熵原理以及基于核密度的非参数估计方法。

2.2.1 最大熵原理

基于最大熵原理的方法通过求解以下优化问题得到连续型随机变量x∈D的概率分布函数f(x)：

式中：Mi为第i阶统计矩。式中目标函数表示最大化信息熵［73］，概率分布越准确则信息熵越大。对上式构造联合约束条件的拉格朗日函数，通过求解拉格朗日乘子，最终可得f(x)，完成不确定性表征。

黄乾坤等［74］围绕基于Shannon 熵的最大熵原理，讨论了不同约束条件下最大熵优化问题的一般形式，并对经典最大熵的不足给出了改进方法。陈雷等［75］针对航空发动机模拟转子叶片，通过最大熵方法拟合了不同叶端定时传感器布局下的测点振幅的概率密度函数，而后通过ANSYS 有限元分析开展了转子叶片动应变重构不确定性量化。Chen 等［76］对模型自身不确定性、模型参数估计的不确定性以及整个模型的不确定性进行了分析，证实了最大熵分布在海洋波高极值计算中的优越性。在数据样本量很小的情况下，样本统计矩所能提供的信息不够丰富和全面，基于最大熵原理的方法所得概率密度分布可能与实际存在较大偏差，为此吕文［77］提出了一种小样本下采用秩来构造约束条件的改进最大熵方法。此外，最大熵方法涉及大量积分计算，积分区间会引入截断误差，且当统计矩最高阶数较大时，会面临求解困难、概率密度积分不为1 等问题，为此李昊燃［78］和刘钰等［79］分别提出了基于转换函数和密度核估计的改进最大熵方法。

2.2.2 核密度估计

假设有n个样本点数据xi(1 ≤i≤n)，传统的核密度估计（KDE）方法求解概率密度函数公式为［72］

式中：K为核函数，常用于KDE 算法中的核函数有高斯核函数、三角核函数、Epanechnikov 核函数等［80］；h为带宽（或窗宽），其通过影响核函数中自变量的取值来控制每个样本的相对权重，影响概率密度的光滑程度和估计精度，可根据最小化AMISE 准则和Silverman 经验法则计算［81］。

单德山等［82］采用核密度估计分析了桥梁构件地震易损性，基于有限元仿真模型构建了桥梁结构构件地震易损性的核密度估计算法。Kang等［83］提出了一种有界数据的核密度估计算法，并对悬臂梁杨氏模量、水平和垂直方向载荷的区间数据进行了核密度估计，发现相较于原始KDE 方法的估计结果更为准确，尤其是样本数据较少时。理论上，只要提供足够多的样本数据，KDE可收敛到任意形状的概率密度函数，即使是在小样本下也可得到概率密度函数的光滑连续估计［84］。但KDE 易出现边界偏差，无法在边界点附近给出良好的估计结果，且拟合的概率密度函数在高密度样本区间过于平滑，缺乏局部适应性。针对该问题，缪鹏彬［85］提出了采用边界核的自适应非参数核密度估计算法。赵铁军［86］对传统KDE 方法进行了改进，将自适应核密度估计与基于伪数据的核密度估计相结合，将伪数据添加到边界附近以修正偏差。

3 面向点数据的不确定性分类表征方法

针对随机不确定性往往依赖测量样本数据获取统计规律的特点，开展面向点数据的不确定性表征建模，Kang 等［69］、Peng 等［41］以及魏骁［87］等学者在这方面作了探索性研究。上述已提到Kang等［69］的研究为如何从随机不确定性多种可能的概率分布中确定最佳分布模型，提供了一条解决思路。但是，当不确定性参数的信息源较少时，单一的概率分布未必能合理表征不确定性。Peng等［41］在各种单一概率分布的基础上引入多种概率分布的混合加权分布作为候选分布模型之一，建立了一种基于拟合优度检验的不确定性变量类型确定方法，对候选模型的拟合优良性给出了定量评价。但该方法采用的AD 检验并不适用于均匀分布，且给出的检验统计量和临界值的计算公式仅适用于正态分布，无法应用于其他概率分布的检验。为此，我们对Peng 等［41］提出的不确定性分类方法进行了改进［88］，采用K-S 检验来满足检验均匀分布的需求，同时定义p值［89］作为拟合优良性的评价指标，使得检验适用于多种分布。

改进的不确定性分类方法将不确定性表征为以下3 种类型的变量，如图4 所示。

图4 随机变量、稀疏变量、区间变量的表征示意Fig.4 Characterization of random variable，sparse variable and interval variable

1）随机变量：数学模型为常见的单一概率分布。

2）稀疏变量：数学模型为多种分布组成的混合加权概率分布。

3）区间变量：数学模型为上下界表达的区间形式。

以下为面向点数据的不确定性表征方法的具体实施步骤。

步骤1判断不确定性变量观测样本个数n，若n＜ncv（临界样本数），则认为不宜拟合概率分布，直接将变量表征为区间变量；否则执行步骤2。

步骤2假设该不确定性变量为随机变量，令变量依次满足m种常见的概率分布，其概率密度函数分别为fi(x)(i=1，2，…，m)。对于不同的研究对象，可根据具体的物理背景选择候选概率分布模型。

步骤3假设该不确定性变量为稀疏变量，令其概率分布为上述除均匀分布外其余m-1 种分布的加权和，其概率密度函数见式（9），根据赤池信息准则［90］为各个概率分布分配权重wi。为了降低模型复杂度，忽略权重小于0.1 的候选概率模型。

步骤 4确定上述分布的fi(x)(i=1，2，…，m)、fmix(x)以及概率分布函数F(x)。基于K-S 检验计算检验统计量Kn，并求解在显著性水平α下的拟合优度（p值），关于p值的计算如下。

1）根据不确定性变量的观测数据，得到其经验概率分布函数Fn(x)。

2）计算KS 距离dKS，在经验概率分布和假设概率分布2 条曲线相交和不相交2 种情况下，KS距离计算的如图5 所示。

图5 KS 距离Fig.5 KS distance

式中：当i=n时，有Fn(xn+1)=Fn(∞)=1；sup表示上确界。

3）由Kn的准确概率分布P(Kn≤dKS)求解p值，p值越大说明拟合程度越优。

式中：tkk的计算详见文献［91］。

步骤5比较拟合优度最大值pmax和显著性水平α的大小，确定不确定性参数的最佳表征形式。若pmax≥α，pmax对应的分布类型为单一概率分布，不确定性变量被表征为随机变量，pmax对应的分布类型为混合加权分布，则被表征为稀疏变量；若pmax＜α，将该不确定性变量表征为区间变量。

不确定性分类表征能够科学合理地表征不确定性变量的类型，并对分布与样本数据之间的拟合优良性进行定量评价，混合加权分布的构建进一步丰富了候选模型库，为随机不确定性从多种可能的一般概率分布中确定最佳的分布模型给出了较为通用的解决方案。该表征方法适用于不确定性信息中仅包含点数据的情况，当点数据和区间数据同时存在时，方法应用受限；同时在候选模型拟合优度均较差的情况下，方法直接将不确定性表征为粗糙的区间变量，如何根据可用的样本数据对区间模型进一步细化和优化也是后续研究需要解决的问题。

4 处理稀疏点和/或区间数据的似然表征方法

上述不确定性表征方法都仅能处理点数据，实际中受时间和经济成本的限制，除了稀疏点数据，可用信息还可能以区间的形式存在。例如与仪器校准相关的不确定性或误差以及试验观测数据的不确定性等，常用区间来描述。图6 为某随机变量X的不确定性信息为稀疏点数据和区间数据，存在3 个点数据｛4.1，5.6，3.8｝和3 个区间数据［3.5，4］、［3.9，4.1］和［5，6］。对此，产生了基于似然理论和基于加权分布的概率表征方法。

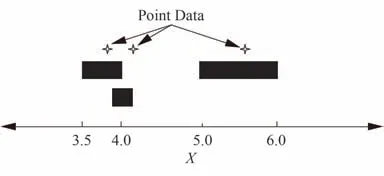
图6 点数据和区间数据同时存在Fig.6 Point data and interval data exist at the same time

通常可用概率理论处理点数据，而处理区间数据则常用区间理论，难以同时用这2 种理论来描述以区间和稀疏点数据存在的随机变量。Sankararaman 和Mahadevan 针对以点数据和/或区间数据存在的随机变量，提出了一种基于似然理论（Likelihood-Based）的方法［40］（以下简称LBM），将信息不充足情况下的随机变量统一用概率模型表征。在该方法的基础上，他们进一步分别利用贝叶斯模型平均和贝叶斯假设检验对分布类型选择导致的不确定性进行量化，进而可在后续的不确定性传播中同时考虑输入参数的随机性、分布参数的不确定性、分布类型的不确定性［92］。张鹏等［93］将这种包含离散数据与区间的变量称为稀疏混合不确定性变量，针对多种候选单一概率分布，分别利用Sankararaman 和Mahadevan［40］提出的LBM 获取不确定性变量的概率密度函数，进一步根据贝叶斯信息准则确定最合适的概率分布类型。

基于LBM 的不确定性表征可分为参数法和非参数法，如图7 所示。参数法需要提前指定不确定性变量的分布类型。然而，在很多情况下有效选择分布类型可能非常困难，而且不同的分布类型假设将导致不同的不确定性表征结果。非参数法避免了对分布类型的假设，且由于不必对分布类型抽样，可显著降低不确定性表征的计算量。接下来将分别对LBM 的2 种实现方法进行介绍。

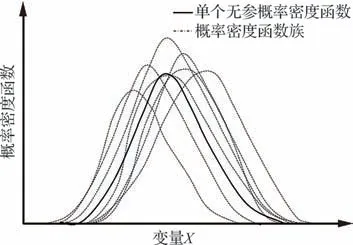
图7 分布族（有参）和单个分布（无参）Fig.7 Family of distributions（parametric method）and individual distributions（nonparametric method）

4.1 LBM 的参数法

设随机变量X存在m个稀疏点数据xi(i=1，2，…，m) 和n个区间数据[ai，bi] (i=1，2，…，n)，且这些数据来源相互独立。fX(x|P)表示X关于P的概率密度函数，P为所需要估计的参数。参数P的似然函数可表示为

不同于直接采用极大似然估计的方法，Sankararaman 和Mahadevan［40］通过全似然估计，利用贝叶斯定理得到分布参数P的概率密度函数。假设fP(P)表示参数P的联合概率密度函数，选择均匀先验概率密度，则分布参数P的后验分布为

根据fP(P)对P抽样可得随机变量X的一族PDF 曲线，导致后续不确定性传播为双层循环，计算量较大。为此，可进一步对分布参数P的不确定性积分从而得到随机变量X的平均PDF。

Sankararaman 和Mahadevan［40］详细给出了求解上式积分的方法。需要注意的是参数法需要提前假设随机变量X的分布类型，但经过积分后所得随机变量X的分布将发生改变，不再与假设相同。

4.2 LBM 的非参数法

非参数法直接基于已有的稀疏数据和/或区间数据，确定随机变量X的最大、最小值边界。然后在最大、最小值形成的区间中将X离散为有限个点qi(i=1，2，…，Q)。pi表示这些离散点上X的PDF 值，即fX(x=qi)=pi。根据这些离散点上的值，利用插值技术可得到其他点上对应的X的PDF 值。令p=(p1，p2，…，pQ)，同理可将似然函数表示为

通过优化如下问题得到p：

Sankararaman 和Mahadevan［40］对PDF 插值的3 种方法——线性插值、样条插值、高斯过程插值进行了详细介绍和探讨，认为高斯过程插值是最为通用的方法。

Peng 等［41］针对基于CFD 数值模拟的曲柄滑块机构和热交换器可靠度评估问题，采用LBM的参数法，完成了混合加权分布的不确定性表征［94-95］。魏骁［87］针对基于CFD 数值模拟的KCS船型优化设计，根据船舶测量设备记录的吃水数据，同样采用参数似然估计对吃水变量的不确定性进行了表征。Peng 等［96］又采用非参数法构建了源于稀疏采样点和区间数据的高斯过程插值模型，提出了稀疏采样点和区间数据多源数据融合方法。

4.3 基于最坏情况最大似然的方法

Zaman 等［97］指出，Sankararaman 和Mahadevan 提出的基于似然理论的不确定性表征方法［40］需要利用贝叶斯更新和积分来获取随机变量的分布，过程较为繁琐，且所得随机变量的分布类型不再与假设分布相同。而且，当所有区间数据均有共同重叠部分时，该方法给出的方差（二阶统计矩）的最大似然估计为零，不再适用，Zaman等［42］认为此时Sankararaman 和Mahadevan［40］提出的方法低估了不确定性。为此，Zaman 等［97］基于似然理论，提出了一种基于最坏情况最大似然估计（Worst-Case Maximum Likelihood Estimation，WMLE）的方法，基于此建立了稳健优化模型，并将其应用于两级入轨飞行器稳健优化问题，对其中的分离飞行轨迹角和长细比进行了不确定性表征［97］。该方法同样可以处理随机变量以稀疏点和/或区间存在的混合数据，也适用于任何类型的多区间数据，即非重叠、重叠以及非重叠和重叠组合的混合区间。

如式（17）和式（18）所示，对于m个稀疏点数据和n个区间数据，基于最坏情况最大似然的方法以外层和内层的2 层嵌套优化来估计分布参数，内层在固定稀疏点数据取值的情况下，对区间数据所有可能取值进行组合计算似然函数值，找到使似然函数最小的区间变量所取的数据值，也就是所谓最坏情况，即区间数据的不确定性所导致的似然下限；外层再通过最大化似然函数，估计分布参数，找到不确定性变量最优的分布参数p。

式中：p为分布参数；x为点数据和区间数据；xlow、xup分别为区间数据的下限和上限。

似然函数值代表概率分布支持现有样本数据的好坏程度，而对于区间数据，观测样本不再是固定的一组值，而是各个区间上所有可能取值的一系列组合。Zaman 等［42］通过搜寻使似然函数最小的这些区间上形成的某组取值，得到概率分布拟合的最坏情况，在该最坏情况下再通过最大化似然函数值来估计参数p的值，这就是基于最坏情况的最大似然的内涵。

上述已经提及，LBM 不适用于所有区间数据均有共同重叠部分的特殊情况，而且无法在仅有一个区间数据的情况下进行不确定性表征，因为此时无论什么形式的概率分布，在该区间上的似然函数值都为1。对此，Zaman 等提出了一种专门应对区间数据的概率表征方法［42］。

当不确定性变量以区间和稀疏点数据混合的形式存在时，除了上述多种基于似然理论的表征方法以外，也有研究直接认定该变量为第3 节不确定性分类中所提到的稀疏变量［41，96］，将其建模为多种单一概率分布混合加权和的形式，见式（9）。

5 处理区间数据的概率表征方法

实际上，不确定性变量的不确定信息源可能为单个或多个区间，多个区间为互不重叠或有重叠的区间。针对单个区间的情况，过去较为常用的做法是直接将区间数据形式的不确定性变量表征为该区间上的均匀分布，相当于认为变量在区间上任意位置出现的可能性是相等的，事实上变量会在区间上的哪个位置出现并不知道，很多研究也指出该处理方式并非合理［98-99］。此外，对于仅存在一个区间信息的不确定性表征问题，上一节中介绍的基于似然理论的方法无法适用。为此，Zaman 等提出了一种专门应对区间数据的概率表征方法［42］，该方法针对单个区间数据、多个互不重叠或有重叠的区间数据的情况，分别给出了统计矩边界计算以及分布拟合的解决办法。

首先建立单个区间的前四阶统计矩的计算方法，在区间上下界的约束范围内进行抽样，并对每个样本点分配概率质量函数（PMF）值，计算各阶中心距E(xk)。前四阶统计矩为

不同的概率质量分配方式对应着前四阶统计矩的无数种可能组合，通过优化即可估计单个区间数据的前四阶统计矩的上下界，找到使单个区间数据的矩最小或最大的区间端点的PMF 值：

Zaman 等［42］研究发现，对于单个区间数据的各阶统计矩的最小值和最大值，PMF 只集中在区间的2 个端点。单个区间数据的统计矩边界随区间下端点处PMF 变化的估计结果曲线，如图8 所示［42］。从图8 中可以看出，当2 个端点的PMF 均为0.5 时，二阶统计矩达到最大值；对于三阶统计矩，估计结果曲线呈对称；对于四阶统计矩，曲线呈双峰形状。

图8 单个区间数据的统计矩边界估计［42］Fig.8 Boundary estimation of statistical moments for single interval data［42］

Zaman 等［42］将单个区间的前四阶统计矩的计算方法扩展到适用于多个重叠或非重叠区间数据的二阶、三阶和四阶统计边界的优化，建立了适用于单个、多个区间数据的统计矩边界计算方法，如式（21）～式（23）所示：

式中：n为区间个数；ai、bi分别表示多个区间数据的下上界端点；xi为在区间中抽取的样本点，即ai≤xi≤bi且i=1，2，…，n。

得到统计矩上下边界后，作者认为每个边界内的各阶统计矩均服从均匀分布，进行抽样，每一组前四阶统计矩的组合都能拟合出有界约翰逊分布，通过大量抽样或基于优化的方式得到所有可能的有界约翰逊分布的分布包络，形成Jonson 概率盒，完成对区间数据的概率表征。图9［42］针对式（24）（多个非重叠区间）和式（25）（多个重叠区间）给出的2 组区间数据，分别展示了所得的Jonson 概率盒，图中粗实线为Jonson 概率盒，阶梯状细实线为数据的经验概率盒，细点线族为前4 阶统计矩的每一组可能组合对应的有界约翰逊分布曲线族。

图9 Jonson 概率盒［42］Fig.9 Jonson p-box［42］

6 随机场表征方法

上述介绍的都是关于单个不确定性参数的表征方法。由于不确定性参数的分散性，不确定性可能随空间的变化而波动，比如随机有限元中的力学空间可变材料特性为输入随机场［100］以及CFD 中雷诺应力的输入随机场［16］，此时单个不确定性参数已无法完整描述整个结构性能的分布。如何准确地描述不确定性参数随空间位置变化的特性，是建立不确定性模型重要的考量。随机场是处理具有空间变异性的不确定性参数的一种表征模型，是解决参数空间分散问题的重要手段。

随机场在其场域内的每个位置均为随机变量，即包含无限个空间相关的随机变量。处理随机场问题要通过点离散、平均离散或级数展开法等离散方法［101］将连续随机场离散为若干个相互独立的随机变量。级数展开法中的Karhunen-Loève（K-L）展开是处理随机场实现维度缩减较为有效的方法［102］。以下对较为常用的K-L 方法进行简要介绍。

设H(x，ω)表示一个随机场，其中x是有界域D ⊂Rd（d∈{1，2，3}）中的空间变量，代表一维/二维/三维空间位置坐标；ω为概率空间中的随机事件。假设随机场H(x，ω)平方可积，具有均值μ、标准差σ和协方差矩阵CH(x，x′)，x和x′为场内两点的空间位置坐标。可使用K-L 展开将H(x，ω)进行如下离散：

式中：μ和分别为随机场的确定性部分和随机部分；n为K-L 截断阶数（级数展开项数）；λi和φi(x)为随机场协方差矩阵CH(x，x′)的特征值和相应的特征函数，满足

随机场表征的核心是如何进行随机场离散，即确定均值μ、标准差σ、协方差矩阵CH(x，x′)的特征值和特征函数，本质上仍然是参数的不确定性表征。不确定性参数μ和σ可基于工程经验给出，也可通过试验测量数据的参数估计得出，CH(x，x′)定义在规则几何空间域上，与场内两点的相关距离有关，而这种相关距离由相关函数体现，常用的相关函数有高斯型、指数型、三角型、指数余弦型、二阶自回归型等［103］。蒋水华对这几种相关函数下的随机场进行了研究，发现高斯型生成随机场连续性较好、效率较高［104］，采用高斯型相关函数计算协方差矩阵的公式为

式中：1 ≤i，j≤n；δk为有界空间域D 的相关距离。

通过上述步骤，将输入随机场离散为了一系列有限个不相关、零均值、单位方差的随机变量ξi(ω)，如果随机场H(x，ω)是高斯随机场，则ξi(ω)形成一组独立的标准高斯随机变量，实现对随机场的不确定性表征，在此基础上就可以进行不确定性传播。

贾超等［105］在地下水力学渗流耦合过程的数值模拟中，考虑到渗透系数作为随机变量的空间变异性，将其不确定性表征为随机场，并根据库区钻孔水位观测资料及库区外围水文地质调查资料确定了随机场模型参数，对地下洞室涌水量进行了预测。Gravanis 等［106］建立了表征岩石边坡稳定问题中岩石材料属性的二维随机场模型，探讨了岩石材料属性的空间变异性对岩石边坡失效概率的影响。牛燚炜等［107］在此基础上提出了三维随机场的建立方法，并把底面摩擦系数和粘聚力视为高斯随机变量，分析了岩石边坡的三维稳定性问题。Feng 等［108］采用均匀随机场表征了各有限元单元弹性模量的不确定性，研究了简支梁和层流板的动力学特性。

7 非概率表征方法

上述不确定性表征方法在建模中主要按照不确定性变量存在的数据形式及数量进行不确定性分类和建模。若将不确定性分为随机和认知两大类，非概率表征方法则为认知不确定性的表征提供了有效建模手段。非概率表征方法往往需要基于专家信息去建立不确定性表征的数学模型，基于不同的数学理论基础形成了如证据理论、区间理论、模糊理论以及凸模型等众多非概率表征方法，呈现出“百花齐放”的局面。

7.1 区间理论

对于许多实际问题，获得不确定参数可能的取值范围要比获取精确概率分布容易得多。当认知水平有限，只清楚参数位于哪个区间，但是不清楚在区间内哪个部分或位置取值的可信度更高时（参数的真值可能取区间中的任意一个值，没有证据或信息表明区间内的任一值比其他值更有可能），可采用区间模型对该参数进行不确定性建模。区间（Interval）模型一般定义为［109］

在区间数学方法中，不确定参数被认为是“未知但有界”，每个不确定性参数都有上限和下限，由一个区间描述，而不具有概率形式。区间AI包含了不确定性参数所有可能的结果，可以包含参数的所有不确定性信息，其中区间中点Ac=(AL+AU)/2 是区间表达的确定性部分，区间半径Ar=(AU-AL)/2 和[-Ar，Ar]构成了区间表达的不确定性部分。区间的不确定性水平γ由区间半径与区间中点比值确定，即γ=Ar/Ac。当不确定性输入包含多个参数时，每个参数对应一个区间数AI，各个区间数组合形成区间向量，对应了不确定性问题的区间模型。

将认知不确定性表征为区间的方式在工程机械、金融经济、环境科学等领域都得到了诸多应用［110-112］。Wong 等［113］采用一阶泰勒展开对损伤结构前后的刚度参数不确定性进行了区间表征，开展了不确定性下的结构损伤判定。刘刚等［114］采用区间数对风力发电系统出力的不确定性进行描述与分析，建立了风电注入功率不确定性的配电网三相区间潮流模拟模型。

基于区间理论的非概率表征方法只需给出确定的上下边界，很大程度降低了对原始数据的要求［115］。区间表征包含了不确定性所有可能出现的情况，经过区间分析后得到的输出响应的区间可能要远大于实际区间，存在“区间扩张”现象［116］，失去工程参考价值。

7.2 概率盒理论

20 世纪90 年代，Williamson 和Downs 在累积分布函数的基础上引入了区间型边界［117］，称之为概率盒（p-box），也称p盒。概率盒定义为一组包含不确定性变量所有可能的累积分布函数曲线的上下边界或概率包络，可以表示为

如图10 所示［118］，概率盒同时适用于随机、认知以及混合不确定性的表征。对于随机不确定性以及单一区间认知不确定性的表征很容易理解，当不确定性变量以多个区间数据存在时，文献［119］提出了“经验概率盒”的概念，定义为给定区间数据集的所有可能的经验分布的集合。由于缺乏对区间数据可信度的分配，经验概率盒认为每个区间数据都是等可能的，因此如果有N个区间数据的话，经验概率盒是2 条具有1/N的恒定垂直步长的递增函数形式的阶梯曲线所构成的不确定区域。图11 和图12 分别展示了文献［119］针对6 个非重叠区间和9 个重叠区间2 种情况下的区间数据集以及相应的经验概率盒，可见每个数据点处的阶梯高度相等，反映了每个区间均被同等加权的假设。

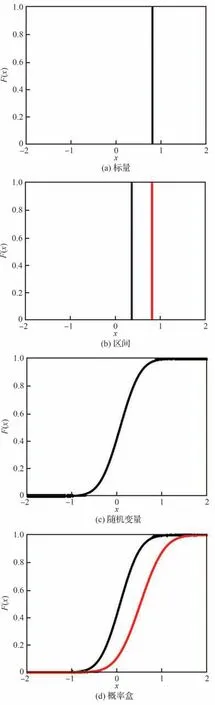
图10 各种形式下的概率盒［118］Fig.10 p-box in various forms［118］

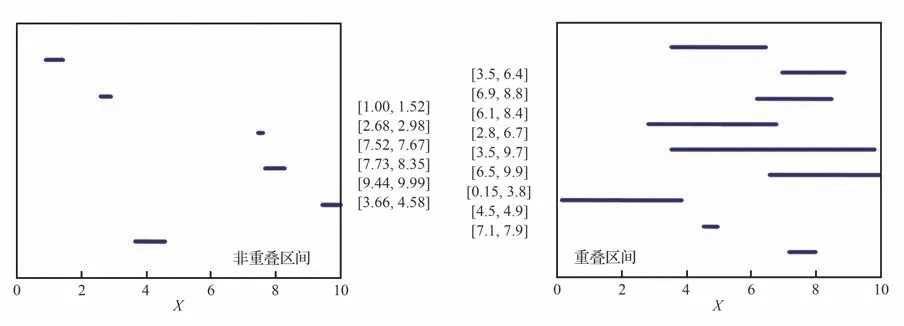
图11 非重叠（左）/重叠（右）区间数据集Fig.11 Non-overlapping（left）/overlapping（right）interval datasets

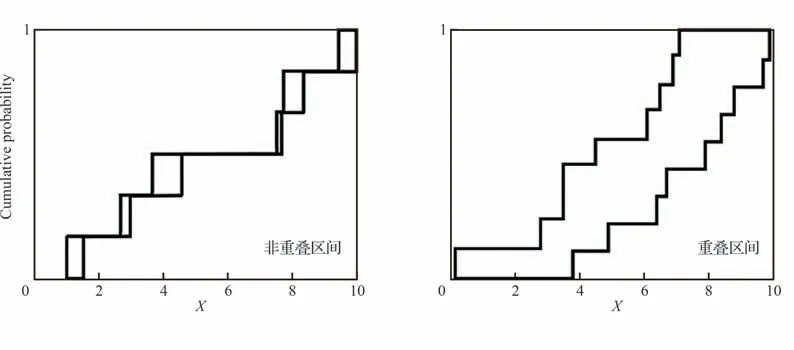
图12 非重叠（左）/重叠（右）区间数据集的经验概率盒Fig.12 Empirical p-box for non-overlapping（left）/overlapping（right）interval datasets

在某些参数的概率分布类型已知，但其分布参数却在一定范围波动的情况下，随机不确定性和认知不确定性耦合在同一个变量中，变量表现出混合不确定性，其数学模型为一族概率分布所形成的概率包络，即给定区间集上所有可能的概率分布的集合，为典型的概率盒。式（31）和式（32）分别以正态分布和均匀分布为例，给出了2 个混合不确定性变量x1和x2的数学模型。如图13所示，随机生成μ以及a和b的80 组值，绘制了变量x1和x2的CDF 函数曲线族。

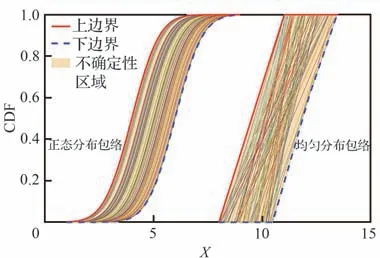
图13 混合不确定性的概率盒表征Fig.13 Characterization p-box-based of mixed uncertainty

概率盒还分为参数化概率盒和非参数化概率盒。参数化概率盒由一族同类型的累积分布函数组成，例如上述所举的混合不确定性表征实例就是典型的参数化概率盒；而非参数化概率盒由边界分布包络的不同类型CDF 曲线组成，其包络的分布函数的形式任意，并不局限于经典的分布函数类型［120］。Zhu 等［121］将汽车客舱复合材料的杨氏模量和密度表征为参数化概率盒，对声压振幅响应进行了不确定性量化。吴沐宸等［120］针对NACA0012 翼型绕流CFD 模拟的不确定性量化问题，根据来流和湍流模型系数的边界分布及其取值范围指定了非参数概率盒变量。

概率盒理论作为一种区间和概率的混合模型，兼顾了区间和概率的特性，现有的区间、概率分布和证据结构都可以转化为概率盒形式，同时适用于随机、认知以及混合不确定性的表征，是一种相对较为通用的不确定性表征方法。但概率盒表征无法直接对来自多个渠道或专家的信息进行融合，证据理论则提供了解决方案。

7.3 证据理论

证据理论起源于1967 Dempster 提出的上下概率理论，他的学生Shafer 对其进行了发展和完善［122］。证据理论通过辨识框架（Frame of Discernment，FD）、基本可信度分配（Basic Probability Assignment，BPA）、信任函数（Belief Function，Bel）和似然函数（Plausibility Function，Pl）的基本概念构成了一个不确定性建模架构。

证据理论下证据变量是表征认知不确定性的最基本变量，证据变量需给定变量的区间描述（通常称为焦元）和相应的BPA（或概率权值），BPA 往往根据工程经验或专家预测确定。以Ai和m(Ai)（i=1，2，…，n）分别表示同一个识别框架上的n个焦元及其BPA。例如证据变量x可以取区间［0，3］上的任意值，但取值落在不同区间［0，1］、［1，2］和［2，3］上的概率不同，分别是0.1、0.6 和0.3，一共有3 个焦元，其对应的BPA 分别为m(x(1))=0.1，m(x(2))=0.6，m(x(3))=0.3。

基于专家意见、仿真数据、测量结果等手段给出的证据是一个非常宽泛的概念，并且各条证据之间相互独立，因此证据理论的基本可信度分配相较于概率满足更弱的公理。根据证据的数学表现形式，基本可信度分配主要有3 种类型：贝叶斯结构（概率结构）、一致性结构（嵌套结构）和一般性结构，如图14 所示［123］。在贝叶斯结构中，辨识框架的每个焦元都会被赋予BPA；在一致性结构中，赋予BPA 的焦元之间有着相互包含的关系；一般性结构是证据最常见的一种形式，顾名思义，BPA 的分配具有一般性和任意性，焦元之间可能存在独立、相交、嵌套等多种关系。形成哪种BPA 结构取决于可用的证据信息。

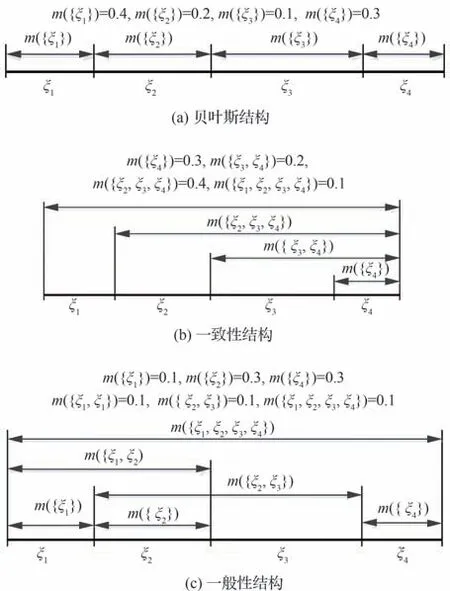
图14 3 种常见的BPA 结构［123］Fig.14 Three common BPA structures［123］

同一个变量的认知不确定性信息可能来自于不同的专家，而不同专家给出的变量区间描述和相应的概率取值往往不同，在证据理论下认为其为多源信息变量，可以按照Dempster 证据合成法则进行多源信息融合，转化为以区间和概率权值描述的证据变量［124］，从而实现多源信息的证据表征。

式中：Bi和Cj分别是来自2 条信息源的证据命题；Ak为合成后的命题；K为冲突系数，表示不同专家给出的证据间的冲突程度，K越大则冲突程度越大。

当存在多个信息源的证据时，需要证据两两之间依次融合，对N条证据重复进行N-1 次操作即可得到最终的融合结果。Dempster 证据合成法则是最经典的证据合成规则，但其不适用于高冲突的证据，因此众多学者又提出了一些改进的证据合成规则，最具代表性的是Yager［125］和Inagakill［126］提出的证据合成公式，它将证据中的冲突部分和未知部分都重新进行了分配，引入比例系数来决定分配的权重。

证据理论使用信任函数Bel 和似然函数Pl 作为不确定性度量的下界和上界。Bel 定义为完全支持命题A成立的所有子集ξ的BPA 加和，Pl 则定义为完全以及部分支持命题A成立的所有子集ξ的BPA 加和。图15 表示信任函数、似然函数、不确定性三者之间的关系，Bel（A）和Pl（A）2 个测度之间的间隔度量了不确定性。

图15 证据理论下的不确定性区间Fig.15 Uncertainty interval based on evidence theory

类似概率理论中的累积概率分布函数（CDF），在证据理论中定义累积信任函数（Cumulative Belief Function，CBF）和累积似然函数（Cumulative Plausibility Function，CPF）分别为Bel 和Pl 构成的概率边界的点集，设不确定性变量x的取值空间为D，有

式中：Θ为不确定性变量x的辨识框架；D为取值空间。

姜潮等［127］在研究汽车侧面碰撞的结构可靠性分析问题时，考虑了某型轿车门梁和B 柱加强板的厚度和材料屈服极限的认知不确定性，通过证据理论进行表征。类似地，范松等［128］在汽车正面碰撞的轻量化设计中，给出了保险杠厚度以及外板厚度等几何认知不确定性的贝叶斯BPA 结构，进行了证据理论下基于有限元仿真的可靠性优化。除了可以直接表征认知不确定性，证据理论也能实现对随机不确定性的表征，胡盛勇等［129］和Shah 等［35］分别将随机不确定变量的概率分布进行离散，得到区间+可信度形式的证据结构，从而在证据理论下进行随机和认知不确定性的统一量化，分别实现了某测试系统的稳健优化设计和RAE 2822 翼型的气动特性分析。

CBF 和CPF 分别是不确定性变量x概率分布的下界与上界，这与上一节中基于概率盒理论的不确定性表征是相通的。文献［130］和［131］也指出，Dempster-Shafer 结构形成的CBF 和CPF 与概率盒二者等价。FULVIO 提出通过平均离散法或外离散法［132］，也可将以概率包络表示的概率盒变量转化为证据结构，将概率盒上下边界的纵向值域[0，1]等离散化为n个子区间，则相应的焦元和BPA 可表示为

基本可信度分配不必满足概率可加性和单调性，因此证据理论满足比概率理论更弱的公理，使得证据理论具备直接表达知识或信息缺乏造成的“不确定”和“不知道”的能力。同时，证据理论中的证据合成公式可以综合不同专家或数据源的知识或数据，能够处理不确定信息、不完备信息、不可靠信息甚至冲突信息，这是证据理论的显著优势。但证据理论要求各条证据之间相互独立，有时这不易满足；并且当变量维数较高时，通过证据理论对不确定性进行传播，焦元上的极值分析计算面临着严重的“维数灾难”。

7.4 模糊理论

模糊理论［133］由Zadeh 教授首次提出。一个经典集合清楚地区分了集合元素和非集合元素，模糊集可看作经典集合的扩展，通过引入隶属度函数来表示域内元素隶属于模糊集的程度，将普通集合的特征函数从{0，1}推广到闭区间[0，1]，得到了模糊集合的定义为［134］

p(x)的大小反映了元素x对集合X的隶属程度，p(x)的值越接近1，说明x隶属于X的程度更高。由上述可知，隶属度函数是常规实数的一般化，隶属度函数不单独引用一个值，而是引用一组可能的值，其中每个可能的值都有自己的权重，其范围为0～1。模糊集合中的每个元素对模糊集合的隶属程度都需要通过隶属度函数来刻画，因此正确合理地建立隶属度函数是表达该模糊集合模糊度和模糊性的关键［135］。常用的隶属度函数的类型主要有高斯型、梯形型和三角型等，关于模糊变量的隶属度函数的确定方法可以参考Medasani 和Kim 等的相关研究［136］。在各种形状的隶属度函数中，三角模糊数（TFN）最流行，其隶属度函数为

式中：a和c分别用于确定三角隶属度函数左右边界；b确定顶峰位置。

如图16 所示，三角隶属度函数的纵轴表示隶属度函数p(x)的取值，α∈[0，1]表示α截集水平，通过特定的隶属度α可以将输入变量截成一系列水平截集，水平截集定义为

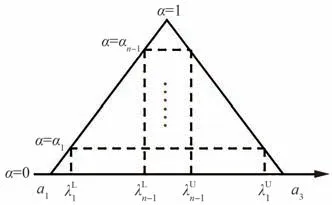
图16 三角隶属函数多水平截集示意Fig.16 Schematic of multi-level cut-sets for triangular membership function

当确定了隶属度函数的类型和参数，即完成了基于模糊理论的不确定性表征，然后在［0，1］上生成不同的截集水平，后续的不确定性传播则相当于一系列的区间分析。徐静等［137］用模糊集概念表征洪水过程模拟中雨量量级的不确定性，运用遗传算法对时段雨量在时间上进行随机解集，并通过在各子流域上采用不同的时间解集模式以同时考虑降雨时程分配和空间分布的不确定性。Mohammadi 等［138］深入研究含能源集线器的电-气联合系统优化调度问题，在计及负荷和风电出力的模糊不确定性的基础，采用梯形隶属度函数建立了预测电价的模糊模型。

不同于经典集合表达的清晰概念，模糊理论通过隶属度函数对模糊现象进行科学描述，使得类似“年轻”“多数”这样的模糊定性问题定量化。隶属度函数的确定类似经典概率统计里分布类型的假设，虽然目前对隶属度函数如何确定有了一些相关研究，但总体来说，仍然相对依赖主观而缺少客观的标准或方法，这也直接影响了基于模糊理论对不确定性表征和传播的准确性。

7.5 凸模型

20 世纪90 年代初，Ben Haim 和Elishakoff［139］提出了处理不确定性的非概率凸模型方法，将参数的不确定性表征为一个凸集合，不像概率表征需要其精确的概率分布，凸模型表征通过较少的样本即可获得不确定参数的边界，因此其在很多复杂工程问题的不确定性分析中展现出很强的适用性。在现有非概率凸模型不确定性表征中，区间模型和椭球凸模型的使用最为广泛。在此基础上，近年来还出现了平行多面体模型、一般多面体凸集模型和超参数凸模型等新型的凸集模型［140-143］。

构造凸模型时只需要确定不确定性参数的边界，而无需考虑内部的概率分布，因此在样本数量有限情况下的不确定性表征建模优势明显［144］。上述提到的区间模型仅通过上下边界描述单个变量的波动，假定所有的不确定参数之间相互独立，其不确定域为超立方体，相关性的忽略使得整个不确定区域和问题解区间变大，导致计算结果精度下降。椭球凸模型将参数不确定性表征为多维椭球，通过椭球的大小和形状描述不确定性的大小以及变量的相关程度［145］，能够很好地处理各不确定参数之间相关的问题。图17为考虑3 个不确定性参数的区间模型和椭球凸模型，可以直观地看出，区间模型不考虑不确定参数的相关性，参数之间相互独立；椭球凸模型考虑参数的相关性，并且边界光滑可导；椭球凸模型避免了一些极端的不确定性参数组合情况的出现，比如出现在三维区间模型角落附近的不确定性参数组合［146］。

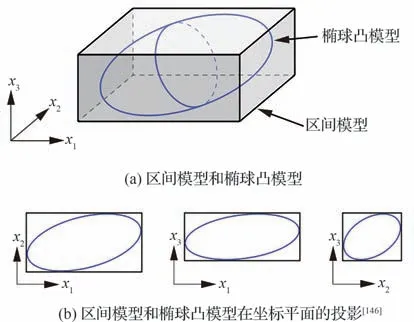
图17 考虑3 个不确定参数的区间模型和椭球凸模型Fig.17 Interval model and ellipsoid convex model considering three uncertain parameters

对任意有界不确定参数x=[x1，x2，…，xn]T，有，椭球凸模型可表示为［147］

已知xi不确定性边界的情况下，基于经验通常取为不确定性的默认值或名义值，可用区间中值替代，ei则为区间边界半径。在已有少量数据样本可用的情况下，还可以采用最小体积椭球法或NATAF 法确定最佳的椭球凸模型参数，关于该方法的具体原理可参考文献［145］和［148］。

Zhu 等［148］提出了一种基于坐标系旋转变换的椭球模型构造方法，该方法遍历基于样本的椭球主轴组合，以此寻找包络样本的最小体积椭球。Jiang 等［145］提出了不确定性多维椭球体的有效建模方法，并建立了非概率凸模型的相关分析技术。Bai 等［149］提出了基于非概率可靠性分析的响应面法，高效地构造了多维椭球体来表征不确定性参数。Kang 等［150］系统地研究构建了在给定一组样本数据的情况下构造最小体积椭球凸模型的数学公式，很好地表征了参数认知不确定性，并展示了它在现有的有界不确定结构非概率可靠性分析和优化设计中的应用。邱志平等提出了多种能高效求解结构在凸模型不确定域上的响应边界的快速算法，形成了众多的研究成果［151-153］。

目前多数文献研究中的椭球模型仍然是基于经验和假设，但对于基于试验数据样本建立椭球模型的研究也逐渐为学术界所关注的重点，使得基于椭球凸模型的参数认知不确定性表征理论也日趋完备。

7.6 不确定理论

为了表征和量化工程实践中广泛存在的随机和认知不确定性，国内外学者进行了很多尝试和研究，发展了上述一些相对比较成熟的理论和方法。清华大学刘宝碇教授近20 年来开创了一种新的研究不确定现象的公理化数学分支，称为不确定理论（Uncertainty Theory），并致力于不确定理论的研究、应用和推广。2007 年德国Springer 出版的《Uncertainty Theory》一书标志着这一理论的正式提出［154］，刘宝碇教授认为：“事件发生的频率已知称为随机，否则称为不确定”，例如掷硬币正面朝上的频率已知，因此是随机的；坠落的蛋糕奶油哪一面着地的频率未知，因此是不确定的。又或，当没有足够样本来估计概率分布时，需要依靠专家的主观信度去评估事件发生的可能性，不确定理论中提出的不确定测度（即信度）成为了解决工具。因此类似于研究随机现象的概率理论，书中提到不确定理论是研究不确定现象的公理化数学系统。

刘宝碇教授发表的多项关于不确定理论的研究成果中，讨论了“不确定理论是什么”“为什么要用不确定理论而不是概率理论”“随机性和模糊性以及不确定之间的关系”等关键问题，给出了不确定理论关于规范性、单调性、对偶性、次可加性的4 条基本公理，定义了不确定空间和变量、不确定测度和分布以及不确定的数学特征、运算法则、基本性质等等，并派生出了不确定统计、不确定规划、不确定过程、不确定集、不确定微分方程、不确定金融等数学分支和研究领域。如图18 所示［155］，刘宝碇教授认为，不确定理论是建立在概率论、可信性理论、信赖性理论3 个公理化体系基础上的数学理论，广义上还包括图中所列的模糊随机理论、随机模糊理论等，即机会理论［156］。

图18 不确定理论树形图［155］Fig.18 Tree chart of uncertainty theory［155］

《Uncertainty Theory》在定义不确定测度（即信度）时提到：不确定测度取决于个人对事件的认识，随着认识状态的变化，不确定测度也会发生变化，因此不确定测度是不确定理论能够表征认知不确定性的关键。为了在实践中应用不确定理论，首先根据不确定测度必须生成不确定分布函数。不确定变量ξ的不确定分布Φ定义为实数集上的函数，对于任意的实数x：

式中：M为件ξ≤x发生的不确定测度。

有了不确定分布的概念，即可通过不确定理论对不确定性进行表征。不确定理论定义了3 种不确定变量及其分布，分别为线性不确定变量L(a，b)、“之”字型不确定变量Z(a，b，c)、正态不确定变量N(e，σ)，对应的不确定分布函数分别见式（44）～式（46）。

在不确定理论中，不确定变量所满足的不确定分布主要由经验和已有的数据规律进行选择，体现了由于认知能力有限对客观规律认识不足所造成的认知不确定性。对不确定分布参数来说，除了可通过少量试验数据进行不确定分布参数a/b/c/e/σ的估计以外（例如不确定极大似然估计方法［157］，将不确定分布函数导数取小），还可以通过专家和经验进行分布参数的主观确定，给出事件发生的信度。因此，不同的不确定分布中的未知参数可通过不确定估计、经验确定和专家指定来获得，从而实现不确定性表征［158］。

杨晗等［158］将不确定理论应用于某牌号Cr-Mo 钢蠕变持久寿命的评估，根据工况经验、手册数据拟合、不确定极大似然估计分别表征了所考虑的4 个蠕变参数的正态不确定分布模型。王瑛等［159］在复杂装备系统风险传递的图形评审技术研究中，基于机会理论对某型战机眼镜蛇机动时飞行员处置不当的不确定性进行了表征，根据部队专家针对飞行员处置不当对飞行安全影响的评价结果，将该不确定性表征为“之”字型不确定分布，通过专家信度确定了分布参数a/b/c。整体来看，不确定理论目前仍处于发展完善之中，研究成果以及工程上的应用主要集中在国内的一些研究人员，较于其它的非概率表征方法而言，不确定理论的工程实践应用仍处于探索阶段。

8 不确定性传播

完成输入量的不确定性表征之后就可进行不确定性传播。对于概率表征方法，由于被表征为概率分布或若干已知分布的加权和，根据该概率分布、加权和分布可非常方便地进行抽样，因此可直接采用基于概率理论的蒙特卡洛仿真或混沌多项式等方法进行不确定性传播［23-24］。

对于区间变量，可单独采用区间、证据、模糊集等诸多认知不确定性处理方法进行不确定性建模和传播，也可采用概率表征方法。采用非概率表征，则要根据选择的方法，基于区间分析、概率盒、证据理论、模糊集、凸模型等各自的理论来解决认知不确定性传播的问题。若同时存在随机和认知混合不确定性，可采用外层概率理论表征随机不确定性、内层非概率方法表征认知不确定性的双层嵌套的方式传播混合不确定性，也可以将不确定性处理到同一个理论框架下进行传播［88］。为了避免双层循环计算量大的问题，文献［41］提出了一种可同时处理随机、稀疏和区间变量的数据驱动混沌多项式方法。Chen 和Qiu 针对随机和区间变量，采用类似的思路构建混沌多项式模型，对复合材料结构进行不确定性分析［160］。Shah 等［35］提出了一种结合证据理论和混沌多项式展开的混合不确定性传播方法，研究了攻角、马赫数、SA 湍流模型系数不确定性对翼型RAE 2822 气动特性的影响。屈小章等［161］基于概率理论和区间分析理论对混合不确定性系统进行可靠性分析，完成了叶片设计参数和叶轮转速对风机气动性能的影响评估。梁霄等［162］结合了概率盒理论和非嵌入混沌多项式方法，分别处理Sod 问题中多方指数的认知不确定性和炸药密度的随机不确定性，并将其应用于流体力学方程组迎风格式数值求解可信度评价的混合不确定性传播。

9 结论和展望

本文面向基于数值模拟的工程设计，综述了参数不确定性表征方法，概述了不确定性表征的研究目的和关键问题。根据不确定性因素的表现形式和可用信息，按照概率表征和非概率表征两大类总结了目前主流的不确定性表征方法，介绍了各种不确定性表征方法的基本原理、适用范围及其在工程实践中的研究、发展和应用现状。

1）不确定性表征的统一和共识

不确定性表征的概率方法均以经典概率统计为理论基础，将不确定性变量建模为概率分布，后续进行不确定性传播时可避免形成非概率表征下的嵌套双重循环而导致的计算量大的问题，同时可非常方便地集成于现有的概率不确定性设计框架，这是其相比于非概率方法的最大优势。但是，当不确定性变量信息非常少时，纯概率表征方法显然会导致较大误差，包含的认知不确定性越大，就越不能用精确的概率分布来描述该量。此时，基于贝叶斯定理的概率表征方法提供了一条有效途径。非概率表征方法在认知不确定性建模上更加合理，尤其当变量信息非常有限时。工程中尤其是航空航天领域由于装备复杂昂贵、工作环境复杂，往往数据量非常少、专家信息也非常有限，小样本下的不确定性表征是长期以来需要攻克的难题。为保证产品性能足够可靠，往往指定不确定变量的上下界，因此区间理论特别适合工程不确定性表征和传播，但后续区间扩张问题比较普遍。各种非概率表征方法基于不同的数学理论，都有其各自优势，难以评价其在认知不确定性表征上的好坏。小样本下，概率和非概率表征方法的合理性以及何种情况下应该用何类、何种方法，尚无广泛认可的评判准则，应该用概率还是非概率表征尚未达成共识。

2）稀疏数据的数据增强

本文综述的不确定性表征方法皆需根据不确定性变量的数据或专家信息对其进行建模。但数据缺乏导致的认知不确定性广泛存在，实际中由于成本限制不可能任意增加物理观测数据，数据增强技术为此提供了一条可借鉴的思路，利用生成对抗网络等深度学习技术或仿真手段来生成不确定性变量的伪数据，从而提高数据量，最终实现较为精确的不确定性概率表征。但是，这类伪数据的可信度如何评价，以及如何有效考虑伪数据的可信度对不确定性表征的影响，是面临的首要难题。

3）认知不确定性的降低

对认知不确定性进行表征和量化的目的是为了降低甚至消除它。很多认知不确定性变量，其并无实际物理意义，比如CFD 数值模拟的湍流模型系数，无法对其进行观测，仅能根据专家经验对其进行不确定性表征，复杂流动问题往往误差很大。此时，可结合贝叶斯推理等统计推断［163］或反向不确定性传播方法［164］，基于输出的流场速度或压力观测数据，对湍流模型系数的不确定性表征模型进行修正，逐步提高参数不确定性表征的合理性，降低认知不确定性，进而更加有效地评估系统输出的不确定性以供设计决策。开发高效的反向不确定性传播方法，尤其是针对高维、强非线性、多不确定性输入且具有不同形式表征的情况，尤为重要。

4）工程基准数据库构建

目前不确定性表征理论和方法研究较为丰富，但多从数理统计领域出发，皆需根据不确定性变量的数据或专家信息对其进行建模，基本都应用于缺乏物理背景的数学问题，距离真正应用于工程还存在很大差距，学术和工业界研究较为脱节。在二者的合作下，可以结合工程问题和专家经验建立若干类型（结构、气动、热等）的不确定性表征基准算例，随着产品生命周期的推进逐步更新不确定性变量的数据信息，以供学术界发展和完善新理论和新方法。比如，美国国家跨声速设施（National Transonic Facility，NTF）建立的不确定性模型，旨在研究气动力/力矩和来流特性等的不确定性［165］。工程基准算例库的构建，可极大促进不确定性表征以及后续传播理论和方法的研究发展，更容易在新旧不确定性表征方法之间达成共识。