任意边界条件下旋转功能梯度锥-柱连接壳行波模态分析

张宇航，刘文光，刘 超

（1.南昌航空大学航空制造工程学院，南昌 330063；2.哈尔滨工业大学深圳理学院，广东深圳 150001）

0 引 言

作为一种新型复合材料，功能梯度材料（functionally graded materials，FGMs）有望应用于船舶推进系统中连接壳的设计。但是连接壳通常服役于复杂的边界条件环境中并伴随着旋转运动，导致连接壳结构出现行波模态，所以研究任意边界下旋转FGMs连接壳的行波模态对于推进FGMs在船舶推进结构的动力学设计应用具有重要价值。

近些年来，关于FGMs 壳的振动问题引起了研究者的广泛关注。基于Rayleigh-Ritz 法，刘超等[1-2]推导了内环向加筋FGMs圆柱壳和含孔隙FGMs圆柱壳的模态频率方程，分析了加筋方式、数量、位置及孔隙率对FGMs 圆柱壳模态频率的影响。引入弹性支撑，黄小林等[3]采用应力函数法推导了FGMs圆锥薄壳的运动学方程，分析了含孔隙的FGMs 圆锥薄壳的振动响应。受实际因素的影响，经典边界通常难以完全实现，众多学者开始致力于研究任意边界条件下壳体结构的振动问题[4-7]。引入人工弹簧技术，Qin 等[7]以改进Fourier 级数、正交多项式和Chebyshev 多项式构造位移函数求解了圆柱壳的自由振动，比较了三者的收敛速度和计算效率，发现Chebyshev 多项式具有较高的计算速度。考虑旋转运动时壳体产生的科氏力和离心力，Bryan[8]研究了自旋转圆柱壳的动力学行为。结合改进的Fourier级数法和Rayleigh-Ritz 法，李文达等[9-10]分析了弹性边界下旋转薄壁圆柱壳的行波模态特性。利用广义微分求积方法（GDQM）[11]，Han等[12]分析了旋转FGMs圆锥壳的动力学特性；Shakouri[13]研究了热环境下旋转FGMs 圆锥壳的自由振动。采用Chebyshev 多项式描述位移容许函数，刘超等[14]分析了任意边界条件下旋转FGMs层合圆柱壳的行波模态特性，分析表明，旋转运动对壳体结构的模态有很大影响，科氏力导致旋转壳行波模态出现分叉现象。

工程实际中，壳体结构往往以连接壳的形式出现。因此，连接壳结构的振动问题也得到了研究者的关注。Irie等[15]采用传递矩阵法，建立了圆锥-圆柱连接壳体的模态频率方程，求解了不同几何参数下连接壳的模态频率。Bagheri等[16-19]研究了不同边界条件下FGMs圆柱壳、圆锥壳和球壳各种组合壳的模态频率。采用分区广义变分和最小二乘加权残值法，瞿叶高等[20-21]将振动问题转化为满足条件下的无约束泛函变分问题，分析了以圆锥壳、圆柱壳和球壳为单元的单壳与连接壳的自由振动问题。采用改进的Fourier 级数法，张帅等[22]研究了锥-柱-球组合连接壳的振动行为。考虑石墨烯增强复合材料和碳纳米管增强材料对壳体结构的作用，研究者探讨了增强复合材料对壳体结构动力学性能的影响。Soureshjani 等[23]分析了热效应对碳纳米管增强圆锥-圆锥连接壳动力学行为的影响；Damercheloo等[24]研究了不同边界条件下石墨烯增强复合材料圆锥-圆锥连接壳的自由振动特性。

虽然研究者对连接壳的振动问题进行了广泛的研究，但大多数研究通常关注静态结构下的驻波模态。由于旋转运动下，离心力会产生环向应力，提高结构的刚度；同时，科氏力会导致频率发生分叉现象，产生前后行波模态，并且由于前后行波频率不同，无法再叠加为常规的驻波模态，因此研究旋转结构的振动问题，只能从行波模态的角度出发。本文以旋转FGMs锥-柱连接壳为对象，采用弹簧模拟结构的任意边界条件和接触边界条件，推导连接壳的模态频率方程，探讨不同参数对旋转连接壳行波模态的影响。研究结果可以为FGMs连接壳的动力学设计提供理论支撑。

1 FGMs连接壳模型

1.1 几何模型

如图1 所示，FGMs 连接壳由圆锥壳和圆柱壳组成。假设两个柱坐标系（xi，θi，zi）分别建立在圆锥壳和圆柱壳中面上，壳体的厚度均为h，并且壳体绕轴线以恒定角速度Ω旋转。壳体的轴向、环向和法向的位移分别为ui、vi、wi，其下标con、cy分别表示圆锥壳和圆柱壳。以该柱坐标系为参照，圆锥壳小端中面半径为R1，大端中面半径为R2，长度为Lcon，半锥角为α0。相应的圆柱壳中面半径为Rcy=R2，长度为Lcy。

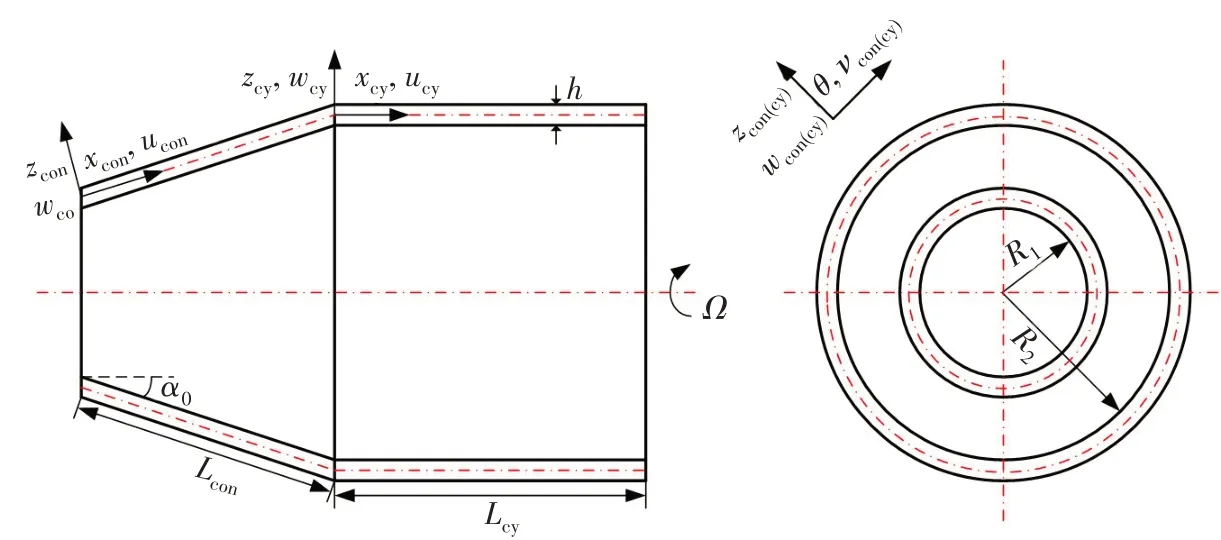
图1 旋转FGMs圆锥-圆柱连接壳的几何模型Fig.1 Geometric model of a rotating FGMs joined conical-cylindrical shell

1.2 材料属性模型

圆锥壳和圆柱壳均采用金属陶瓷材料作为梯度组分，采用幂律函数来描述陶瓷材料沿厚度方向上的体积分数[13]为

采用Voigt模型，FGMs沿壳体厚度方向的有效参数可以定义为

式中，N表示陶瓷体积分数指数，Vmi、Vci分别为金属和陶瓷的体积分数，Pmi、Pci分别为金属和陶瓷的材料属性，Pi为FGMs圆锥壳和圆柱壳的有效材料属性。

因此，FGMs连接壳的材料属性如弹性模量E、密度ρ、泊松比v可分别表示为

式中，下标m、c分别表示金属材料和陶瓷材料。

1.3 边界连续性模型

如图2所示，在结构的两端与圆柱-圆锥壳的连接处分别定义了4组连续分布的弹簧，以模拟任意边界条件和连接处的连续性。在xcon=0和xcy=Lcy处设置轴向弹簧ki

图2 边界约束弹簧和连接弹簧Fig.2 Boundary constraint springs and connecting springs

1、环向剪切弹簧ki2、径向剪切弹簧ki3与扭转弹簧ki4。同样在xcon=Lcon和xcy=0 处设置轴向弹簧kcon-cy1、环向剪切弹簧kcon-cy2、径向剪切弹簧kcon-cy3、扭转弹簧kcon-cy4。连接处的位移所满足的连续性条件可表示为

2 模态频率方程

2.1 应力应变方程

根据Love薄壳理论，连接壳的应变分量与中面位移的关系[22]可定义为

2.2 能量方程

根据弹性力学，FGMs连接壳的应变能Us可以表示为

壳体旋转时产生的动能K由方程（17）和（18）表示，环向应力产生的初始应变能Uh由方程（19）和（20）表达。根据1.3 节中连续性条件，储存在边界弹簧和接触弹簧中的弹性势能Ue可由方程（21）～（23）表达。

式中，上标“·”表示对时间的一阶导数；Ω的0次项表示因变形产生的动能；Ω的1次项表示因科氏力产生的动能；Ω的2次项表示因离心力所产生的动能；Ii

1表示惯性矩，表达式为

需要指出的是，当令转速为0 时，结构简化为静止结构，其同样适用于本文的方法进行模态分析。

2.3 位移方程

假设环向波数取n时的位移方程为

用Chebyshev多项式展开振型函数以模拟任意边界条件和接触连续性条件：

2.4 频率方程

构造拉格朗日能量函数

式中，M1、M2、K分别表示质量阵和刚度阵。

求解式（32）可得到旋转连接壳的前后行波模态频率。与旋转方向一致且小于0为前行波模态频率，相反为后行波模态频率。为了更好地比较前后行波模态，取前后行波模态频率的绝对值分析。定义无量纲转速和无量纲频率：

式中，ωb和ωf分别表示连接壳的后行波模态频率和前行波模态频率。

3 模型验证

3.1 收敛性分析

假设FGMs 连接壳的几何参数分别取：R1/Rcy=0.4，Lcy/Rcy=2.5，Rcy/h=100，α0=30°。材料参数分别取Em=2.08×1011Pa，Ec=3.22×1011Pa，ρm=8166 kg/m3，ρc=2370 kg/m3，vm=0.3177，vc=0.3。轴向波数m取1。如无特殊说明，以下数值计算取的参数不发生改变。

因模态频率与Chebyshev 多项式的截断项数以及弹簧刚度取值有关，图3 首先分析了Ω=0 时，连接弹簧和边界弹簧刚度值的收敛情况。结果表明，无论是连接弹簧还是边界弹簧，弹簧刚度值大于1012时，模态频率收敛。

图3 弹簧刚度收敛性分析（A=6）Fig.3 Convergence analysis of spring stiffness（A=6）

本文连接弹簧刚度值取1013，而边界弹簧刚度值为0时视作自由边界；边界弹簧刚度为1013时视作固支边界。因此，改变弹簧的刚度值可模拟不同的边界条件。表1所示是自由（F）、简支（S）、固支（C）各种经典边界对应的弹簧刚度取值。表2分析了自由边界条件下连接壳（R1/Rcy=0.4226，Rcy/Lcy=1，Rcy/h=100，α0=30°，Em=2.11×1011Pa，ρm=7800 kg/m3，vm=0.3）的无量纲模态频率ϖ。

表1 经典边界下弹簧刚度值Tab.1 Spring stiffness values with classical boundary conditions

表2 自由边界条件下连接壳频率收敛性分析Tab.2 Convergence analysis of joined shell with free boundary conditions

结果表明，壳的模态频率随截断项数的增加逐渐趋于收敛。所以，后续分析过程中取截断项值Ai=10。

3.2 有效性分析

将连接壳简化为静态均质圆柱壳、旋转均质圆柱壳和旋转FGMs圆锥壳以验证模型的有效性。表3 对比了不同边界均质圆柱壳（Lcy/Rcy=2，Rcy/h=500，Em=7.102×1010Pa，vm=0.3，ρm=2796 kg/m3）的模态频率。表4 显示了简支边界下旋转均质圆柱壳（Lcy/Rcy=5，R2/h=500，Ωd=0.0013，Em=1.6806×1011Pa，vm=0.3，ρm=3000 kg/m3）的前行波模态频率变化情况。通过与文献[12]微分求积法（DQM）和文献[28]广义微分求积法（GDQM）所得结果的对比，表5 分析了旋转FGMs圆锥壳（Lcon/R1=2.5，R1/h=20，Ωd=0.025，n=1，α0=45°，N=1）的后行波模态频率随圆锥角的变化情况。

表3 均质圆柱壳模态频率对比Tab.3 Comparison of frequencies of an isotropic cylindrical shell

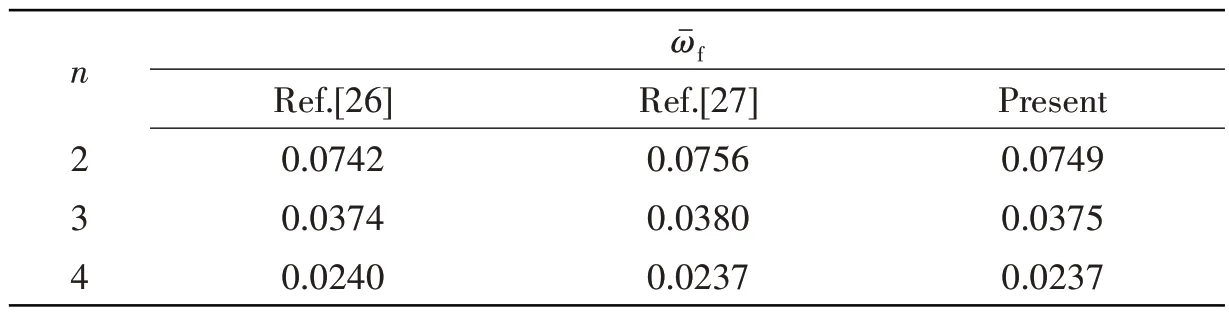
表4 旋转均质圆柱壳前行波频率对比Tab.4 Comparison of frequencies of forward wave of a rotating isotropic cylindrical shell

表5 旋转FGMs圆锥壳后行波频率对比Tab.5 Comparison of frequencies of backward wave of a rotating FGMs conical shell

结果表明，本文计算结果和文献吻合性良好，说明了理论模型的合理性。同时，对于不同边界条件只需要改变弹簧的刚度取值，就可大大降低构造满足边界条件的位移函数的复杂性。

4 行波模态频率分析

4.1 环向波数的影响

图4 比较了Ωd=0.003 时不同边界条件下旋转FGMs连接壳行波模态随环向波数的变化。结果表明，后行波频率始终大于前行波频率，两种频率均随着波数的增大呈先减小后上升趋势。在C-C 和S-S 边界下，结构最低的频率都出现在环向波数取5 的情况，而对于F-C边界，则出现在取值为3时。后续研究中，为了避免结构发生低频共振，选用对应最小频率下的波数进行分析。

图4 不同的环向波数下的行波模态频率Fig.4 Traveling wave frequencies with different circumferential wave numbers

4.2 体积分数指数的影响

图5分别比较了Ωd=0.001、0.003、0.005时，体积分数指数对FGMs锥-柱连接壳前后行波模态频率的影响。结果表明，前后行波模态频率都随体积分数指数N的增大呈下降趋势。这是由于N越大，壳体中的陶瓷含量降低，结构刚度下降。随着转速的增大，后行波模态频率上升，前行波模态频率下降，前后行波的分叉越发明显。在F-C边界条件下，前后行波模态频率随转速和体积分布指数变化最小。可以发现，当N＞5 后，频率变化对陶瓷体积分数的敏感度进一步降低，即对于旋转FGM 结构，通过调节N的大小可以在不改变结构模态频率的基础上，得到工程中所需要的材料性能，如陶瓷含量增加所提高的耐热性、金属含量增加所提高的耐腐蚀性。

图5 不同体积分数下的行波模态频率Fig.5 Traveling wave frequencies with different volume fraction exponents

4.3 旋转速度的影响

图6研究了圆锥角α0=30°、45°、60°时转速对前后行波模态频率的影响。结果表明，不同边界条件下，模态频率对于锥角的敏感程度为：F-C＞S-S＞C-C。在F-C 边界条件下，前行波的模态频率随转速的增大而下降，并将出现零频率。因此，实际中考虑F-C边界条件下，转速不宜取过大，从而避免结构失稳。不同于F-C边界，C-C和S-S边界条件下，前行波模态频率随转速增大先下降后上升。

图6 不同旋转速度下的行波模态频率Fig.6 Traveling wave frequencies with different rotational speeds

4.4 边界条件的影响

工程实际中，结构所处的边界非常复杂，因此接下来分析任意边界下连接壳的行波模态。取Ωd=0.003，图7 和图8 分别研究了k1i=k4i=0 时，由F-F 边界变化到S-S 边界连接壳前后行波模态频率的变化和k2i=k3i=1013时，由S-S 边界变化到C-C 边界连接壳前后行波模态频率的变化。结果表明，环向弹簧k2i和径向弹簧k3i对旋转FGMs连接壳的行波模态影响类似。当弹簧刚度取10-4～106时，结构的行波模态几乎不受影响。而当刚度在106～1012时，前后行波模态频率呈线性上升的趋势，最后收敛在1013处。行波模态在k1i取10-4～108时，k4i取10-4～104时，轴向弹簧k1i和扭转弹簧k4i的共同作用几乎不受影响。在k1i取108～1012以及k4i取104～108时，结构的行波模态频率快速上升，且最终分别收敛于1013、109，因此轴向弹簧的收敛速度要远低于扭转弹簧，其对结构行波模态的影响远大于扭转弹簧。可以看出，在弹性边界时，结构行波模态变化明显，因此采用弹簧模拟边界条件是必要的。

图7 两组弹簧刚度（ki2，ki3）对旋转FGMs锥-柱连接壳行波模态的影响Fig.7 Effects of two kinds of boundary spring stiffness coefficients（ki2，ki3）on the traveling wave mode for a rotating FGMs joined conical-cylindrical shell

图8 两组弹簧刚度（ki1，ki4）对旋转FGMs锥-柱连接壳行波模态的影响Fig.8 Effects of two kinds of boundary spring stiffness coefficients（ki1，ki4）on the traveling wave mode for a rotating FGMs joined conical-cylindrical shell

由图6可知，转速对壳体的行波模态影响明显，因此图9探究了转速和单组弹簧刚度共同影响下，旋转FGMs锥-柱连接壳的行波模态变化。除所讨论的边界弹簧刚度外，其他边界弹簧刚度值取1013。

图9 单组弹簧刚度和旋转速度对旋转FGMs锥-柱连接壳行波模态的影响Fig.9 Effects of single boundary spring stiffness coefficients and rotational speed on the traveling wave mode for a rotating FGMs joined conical-cylindrical shell

分析发现，轴向弹簧（k1i）对连接壳的行波模态影响最大，环向弹簧（k2i）对连接壳的行波模态作用最小，而径向弹簧（k3i）和扭转弹簧（k4i）所产生的效果类似。相比后行波模态，前行波模态对边界弹簧刚度更为敏感，在弹簧刚度取106～1012时，模态频率呈现显著上升的趋势。随着转速的提高，后行波模态一直呈现上升态势。对于前行波模态，频率总是先减小，而当转速高于0.004 时呈现增大趋势。在改变环向、径向以及扭转弹簧刚度时，旋转FGMs锥-柱连接壳行波模态频率主要受转速的影响。而在轴向弹簧与转速共同作用时，轴向弹簧对连接壳的行波模态起主要作用。

5 结 论

本文采用弹簧模拟旋转FGMs 锥-柱连接壳的任意边界条件和连接条件，推导了旋转连接壳在考虑科氏力和离心力作用下任意边界条件的理论模型，利用Chebyshev多项式和Rayleigh-Ritz 法求解了结构的行波模态频率，分析了各种参数对行波模态的影响。主要结论如下：

（1）采用人工弹簧技术，有效实现了实际工程中的弹性边界，在计算求解过程中，相比于传统能量法，减少了大量重复的计算，提高了计算效率。

（2）随着陶瓷体积分数的增大，旋转FGMs锥-柱连接壳前后行波模态频率呈现下降趋势，当N＞5后，行波模态频率的变化趋势逐渐平缓；工程实际中，可以通过合理设计N以突出梯度材料组分中某一材料的优越性能。

（3）由F-F 边界过渡到S-S 边界，环向弹簧刚度（ki2）和径向弹簧刚度（ki3）对结构行波模态的影响趋势基本一致，且行波模态收敛所对应的弹簧刚度都为1013；由S-S边界过渡到C-C边界，轴向弹簧刚度（ki1）相对扭转弹簧刚度（ki4）对结构行波模态的影响更明显，弹簧刚度分别取ki1＞1013、ki4＞109后，行波模态频率趋于收敛。

（4）针对短薄连接壳结构，轴向弹簧刚度对其行波模态影响最为显著，而轴向弹簧相较于转速对行波模态又有更显著的影响；在临界转速之前，前行波模态频率呈下降趋势，之后上升；当结构在临界转速工况下，前行波模态频率最小，结构更容易发生失稳，实际中应该避免临界转速的工况。