部分浸没充液无限长圆柱壳声辐射特性研究
2024-01-19王文涛周富霖
王文涛,王 斌,范 军,周富霖
(上海交通大学海洋工程国家重点实验室高新船舶与深海开发装备协同创新中心,上海 200240)
0 引 言
壳体是工程应用中的常见结构,例如系泊的潜艇、水面舰船、油气运输管道等均可简化为部分浸没的充液圆柱壳。近些年来,单层圆柱壳、双层圆柱壳[1]和内部加肋圆柱壳[2]等的声振特性被广泛研究,但是大多聚焦在全无限流体域中,忽略了自由液面边界的影响,因此本文开展部分浸没充液圆柱壳的研究,重点关注浸没深度和充液高度对其辐射声场的影响。
在现有研究中,Salaün[3]建立了半浸没状态下无限长圆柱壳声辐射的解析模型,研究表明自由液面对半浸没圆柱壳辐射声场具有重要影响;王斌等[4]研究了半浸没无限长圆柱壳的振动和声辐射特性,通过对比激励力位于液面上方及下方时壳体的均方振速和辐射声功率,得出壳体均方振速受激励力位置影响较小的结论;叶文兵[5]基于Flügge薄壳理论建立了半潜无限长圆柱壳振动和声辐射的解析模型,将壳体周围流体域近似为扇形,得到了部分浸没圆柱壳振动的近似理论模型,这些工作为后续研究部分浸没圆柱壳的振动和声特性奠定了理论基础。当壳体部分浸没时,壳体与流体之间的耦合面会随着浸没深度变化,严格解析解较难获得,大多采用数值仿真计算方法,因此Ergin[6]和Adams[7]等利用有限元方法讨论了部分浸没在流体中的圆柱壳自由振动特性。关于部分浸没真空圆柱壳的声辐射研究已较为成熟,而针对内部充液圆柱壳的研究,Li[8]通过波数域方法研究了半浸没全充液圆柱壳在流动的流体中的声辐射特性,并指出辐射声场与激励点位置、流体流速和壳体厚度有关;林子钦等[9]利用附带水质量法讨论了部分浸没充液圆柱壳的自由振动特性。但是上述工作对于壳体中弹性波的研究大多聚焦在定量分析而未对其机理进行深入讨论。
本文首先利用有限元软件COMSOL 建立半充液无限长圆柱壳和半浸没无限长圆柱壳的仿真模型。然后,为了研究壳体浸没深度变化对辐射特性的影响,计算了半充液无限长圆柱壳辐射声压的频率-浸没深度谱,为了研究壳体充液高度对辐射特性的影响,计算了半浸没无限长圆柱壳辐射声压的频率-充液高度谱。考虑到在后续的研究中方便与现有实际模型对比,计算参数取壳体中面半径a=0.1365 m,厚度hs=0.004 m,材料为钢,密度ρs=7850 kg/m3,杨氏模量Es=1.94201×1011Pa,泊松比σs=0.25;水介质密度ρf=1000 kg/m3,声速cf=1500 m/s,结果中呈现出两种不同的辐射共振亮线。最后,通过对壳体中弹性环绕波的激发、传播路径以及辐射的研究,分析了共振现象的产生机理,并给出共振频率的预报公式。
1 仿真建模
假设圆柱壳为弹性薄壳,沿轴向无限长,顶部施加轴向线激励F。以壳体截面圆心为原点建立柱坐标系(r,φ,z),其中φ的取值范围为0到2π。
对于部分浸没半充液无限长圆柱壳,其浸没深度动态变化,引入参量h表示壳体底部与外部流体液面间的距离,仿真模型示意图如图1所示。

图1 部分浸没半充液圆柱壳仿真模型示意图Fig.1 Simulation model of partially-immersed semi-filled cylindrical shell
为了方便对计算结果的观测,引入归一化浸没深度H,令H=(h-a)/a。当壳体下表面刚刚接触外部流体自由液面时H=-1;当壳体恰好完全浸没于壳体外部流体时H=1。因此当H的变化范围为-1~1 时表示壳体连续下潜的过程。远场辐射声压观察点取在壳体正横位置的正下方100 m 处(r=-100,φ= 3π 2,z= 0)。力源激励频率范围为20~5000 Hz。
在COMSOL 软件中添加二维轴对称几何,并设置上文所述参数和相应的区域以及边界条件,建模结果如图2所示。

图2 部分浸没半充液无限长圆柱壳建模结果Fig.2 Modeling result of partially-immersed semi-filled infinite cylindrical shell
然后扫描归一化浸没深度和激励频率,可以得到不同浸没深度下圆柱壳远场辐射声压的频谱结果,最终可得到壳体远场辐射声压的频率-浸没深度谱。
对于半浸没部分充液无限长圆柱壳,建立相同的壳体结构坐标系,如图3所示。
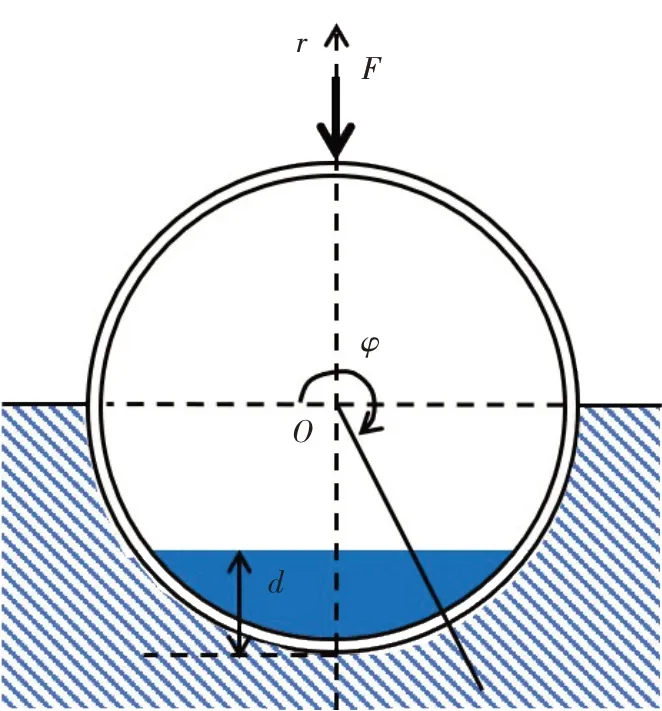
图3 半浸没部分充液圆柱壳仿真模型示意图Fig.3 Simulation model of semi-immersed partially-filled cylindrical shell
壳体内部充液高度为d,为了方便对计算结果的观测,引入归一化充液高度D,令D=(d-a)/a。当壳体内部真空时D=-1,当壳体内部完全充液时D=1。因此当D的变化范围为-1~1 时表示壳体连续充液的过程。
在COMSOL软件中采用类似的建模方法,得到的结果如图4所示。

图4 半浸没部分充液无限长圆柱壳建模结果Fig.4 Modeling result of semi-immersed partially-filled infinite cylindrical shell
通过扫描归一化充液高度和激励频率,可以得到不同充液高度下圆柱壳远场辐射声压的频谱结果,最终得到壳体远场辐射声压的频率-充液高度谱。
上述两种工况的模型计算均属于振动问题,在COMSOL 计算过程中只扫描参数的变化,原理相同。
2 半充液圆柱壳浸没深度对声辐射特性的影响研究
本章主要研究半充液圆柱壳辐射声场随浸没深度的变化规律,通过对辐射声压的频率-浸没深度谱的分析,基于弹性环绕波理论对结果中呈现出的共振现象做出机理解释。
基于第1章仿真模型和计算方法可以得到半充液圆柱壳辐射声压的频率-浸没深度谱,结果如图5 所示。其中:颜色代表声压幅值,单位为Pa;纵轴为圆柱壳归一化浸没深度H;横轴为力源激励频率f。
图5中呈现出两种明显特征:一是存在一系列规律分布且大致平行的倾斜亮线,这是由壳体内弯曲波a0辐射共振产生的[10];二是存在两段独立分布的共振亮线,如图中红色虚线框标注所示,说明壳体内还存在其他形式的波。两种特征均与激励频率以及浸没深度有关。
首先分析a0波的辐射共振规律,a0波在壳体中的传播速度分为两种情况:一是壳外流体液面低于充液液面,如图6所示;二是壳外流体液面高于充液液面,如图7所示。

图6 部分浸没半充液圆柱壳弯曲波传播路径情况一:外部流体低于充液高度Fig.6 Propagation path of bending wave of semi-filled cylindrical shell with the liquid level higher than external fluid level

图7 部分浸没半充液圆柱壳弯曲波传播路径情况二:外部流体高于充液高度Fig.7 Propagation path of bending wave of semi-filled cylindrical shell with the liquid level lower than external fluid level
对于情况一,圆柱壳浸没在水中,壳体外部与水面交于A1、B1两点,壳体内部与水面交于A2、B2两点。以顺时针传播为例,a0波的路径为A1—>A2—>B2—>B1—>A1,会途经壳体两侧均为真空的部分(A2—>B2)、壳体外部真空内部充液部分(A1—>A2、B2—>B1)和壳体两侧均为水的部分(B1—>A1)。设a0波在其中的相速度分别为。根据不同部分传播的相速度,可以得到共振频率的预报公式:
随着壳体浸没深度的增加,θ1逐渐减小,共振频率f逐渐减小,所以共振峰随着浸没深度的增加向低频方向倾斜,在频率-浸没深度谱上呈现出从左上到右下的共振亮线。
对于情况二,壳体外部与水面交于A4、B4两点,壳体内部与水面交于A3、B3两点。同样以顺时针传播为例,a0波的路径为A4—>B4—>B3—>A3—>A4,会途经壳体两侧均为真空的部分、壳体外部浸水内部真空部分(B4—>B3、A3—>A4)和壳体两侧均为水的部分。设a0波在B4—>B3、A3—>A4段传播的相速度为,由此可以得到共振频率的预报公式:
随着壳体浸没深度的增加,θ2逐渐增大,共振频率f逐渐减小,共振峰分布向低频倾斜。
由于浸没状态下的充液圆柱壳频散曲线较难获得,且a0波在圆柱壳中的传播速度与在平板中的传播速度相似,可通过相同材料、相同厚度的板中波的相速度频散曲线预报辐射共振。通过谱方法计算两侧真空的钢板、一侧真空一侧水的钢板和两侧均为水的钢板等三种工况的频散曲线,结果如图8所示。

图8 不同工况钢板的相速度频散曲线Fig.8 Phase velocity dispersion curve of different steel plates
图中横轴表示激励频率,纵轴表示不同工况钢板中a0波波速与水中声速的比值。黑色实线表示两侧均为真空的钢板中a0波相速度频散曲线(c值),红色虚线表示一侧真空一侧为水的钢板中a0波的相速度频散曲线值),蓝色点划线表示两侧均为水的钢板中a0波的相速度频散曲线(c值)。基于预报公式和频散曲线,将计算出的预报结果添加至辐射声压的频率-浸没深度谱中,结果如图9所示。

图9 a0波共振预报结果与数值计算结果对比Fig.9 Comparison between the prediction results and the numerical results of a0 wave resonance
图中白色虚线即为预报结果,可以看出预报结果与数值仿真计算结果中的亮线吻合得很好,说明导出的预报公式能够准确地解释共振现象。此外,声压的频率-浸没深度谱中除了a0波贡献的倾斜条纹外,还存在独立分布的共振亮条纹,这是由于壳体内被激发出的一系列流体附加波导致的。流体附加波只在壳体内表面流体中往返传播[11],路径如图10 中白色曲线所示。

图10 流体附加波传播路径Fig.10 Propagation path of fluid additional wave
可见流体附加波往返传播会激发较强的辐射共振,为了导出共振频率的预报公式,需要计算半充液圆柱壳中各种波的相速度频散曲线。已知壳体浸没对流体附加波的传播影响很小[12],因此本章仅针对外部真空状态下的半充液圆柱壳模型展开计算,为了避免手动插值造成结果不准确,采用COMSOL 仿真计算求解,结果如图11所示。
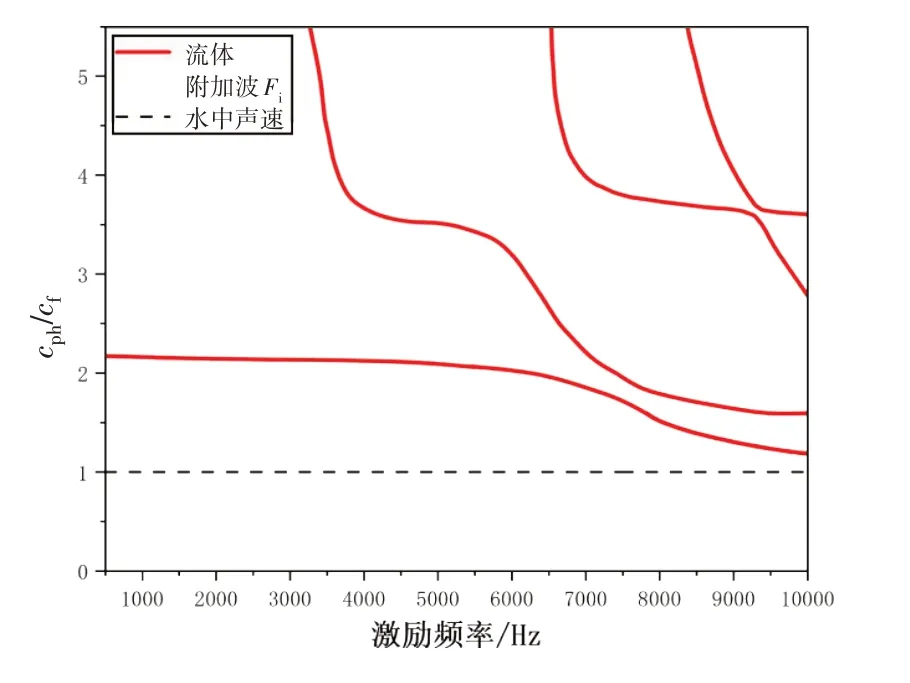
图11 半充液圆柱壳中流体附加波相速度频散曲线Fig.11 Phase velocity dispersion curve of fluid additional wave in semi-liquid filled cylindrical shell
图中横轴表示激励频率,纵轴表示真空中半充液圆柱壳内流体附加波Fi的波速与水中声速的比值。在研究频段内,起主要贡献作用的是低阶流体附加波F0和F1。由于壳体内部恒为半充液,因此共振频率的预报公式为

图12 流体附加波共振预报结果与数值计算结果对比Fig.12 Comparison of prediction results and numerical calculation results of fluid additional wave resonance
图12 中红色虚线表示F0波激发的共振峰,红色“*”线表示F1波激发的共振峰。趋势吻合说明推导的预报公式可以预报辐射声压的频率-浸没深度谱中的共振现象。但是在数值计算结果中,当H在-1~0 范围内变化时,流体附加波的辐射很弱,起主要贡献作用的是F0波,相速度几乎不变,表现为不随浸没深度变化的共振条纹;当H在0~1 范围内变化时,起主要贡献作用的是F1波,表现为随浸没深度变化的弯曲亮条纹,其中的原因有待进一步研究。
3 半浸没圆柱壳内部充液对声辐射特性的影响研究
接下来研究半浸没圆柱壳辐射声场随壳体内部充液高度的变化规律,通过对辐射声压的频率-充液高度谱的分析对呈现出的共振现象做出机理解释。
采用相同计算参数,得到半浸没圆柱壳辐射声压的频率-充液高度谱,结果如图13所示。其中颜色代表声压幅值,单位为Pa;纵轴为圆柱壳归一化充液高度D;横轴为力源激励频率f。

图13 半浸没圆柱壳辐射声压频率-充液高度谱Fig.13 Frequency height spectrum of radiated sound pressure of semi-immersed cylindrical shell
从图13 中可以观察到一系列规律分布的由a0波激发的共振峰和一条独立的由Fi波激发的共振峰。首先分析a0波辐射共振机理,a0波的传播也分为两种情况:一是充液高度低于浸没深度,如图14所示;二是充液高度高于浸没深度,如图15所示。

图14 半浸没部分充液壳体弹性波传播路径情况一:充液高度低于浸没深度Fig.14 Propagation path of elastic wave in partially-filled cylindrical shell with the lower filling height

图15 半浸没部分充液壳体弹性波传播路径情况二:充液高度高于浸没深度Fig.15 Propagation path of elastic wave in partially-filled cylindrical shell with the higher filling height
对于情况一,圆柱壳半浸没在水中,壳体外部与水面交于C2、D2两点,壳体内部与水面交于C1、D1两点。以顺时针传播为例,a0波的路径为C1—>C2—>D2—>D1—>C1,会途经壳体两侧均为真空的部分、壳体外部浸水内部真空部分和壳体两侧均为水的部分。根据不同部分传播的相速度,可以得到共振频率的预报公式:
随着壳体浸没深度的增加,γ1逐渐减小,共振频率f逐渐减小,所以共振峰随着浸没深度的增加向低频方向倾斜,在频率-浸没深度谱上呈现出从左上到右下的共振亮线。
对于情况二,壳体外部与水面交于C3、D3两点,壳体内部与水面交于C4、D4两点。同样以顺时针传播为例,a0波的路径为C4—>D4—>D3—>C3—>C4,会途经壳体两侧均为真空的部分、壳体外部真空内部充液部分和壳体两侧均为水的部分,由此可以得到共振频率的预报公式:
随着壳体浸没深度的增加,γ2逐渐增大,共振频率f逐渐减小,共振峰分布向低频倾斜。
由于预报公式中需要的a0波在不同部分的相速度均在图5中给出,因此可直接对共振峰进行预报,将预报结果添加至辐射声压的频率-充液高度谱中,结果如图16所示。

图16 a0波共振预报结果与数值计算结果对比Fig.16 Comparison between the prediction results and the numerical results of a0 wave resonance
图中白色曲线即为预报结果,可以看出预报结果与数值仿真计算结果中的亮线吻合得很好,说明了预报公式的准确性。接下来分析流体附加波的共振机理,其传播路径与上一章分析的类似,限于篇幅,在此不重复描述。计算外部真空全充液圆柱壳中各种波的相速度频散曲线,结果如图17所示。
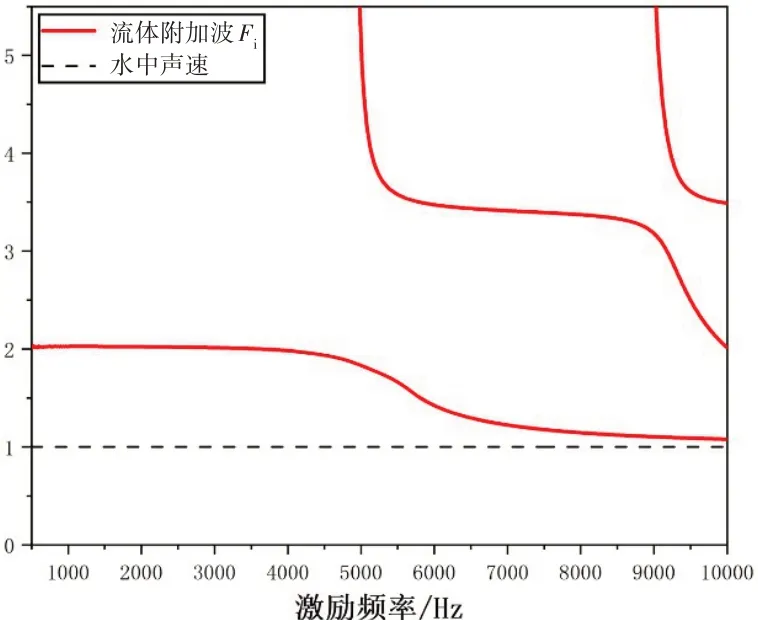
图17 全充液圆柱壳相速度频散曲线Fig.17 Phase velocity dispersion curve of fully-filled shell
图17中横轴表示激励频率,纵轴表示真空中的全充液圆柱壳内流体附加波Fi波速与水中声速的比值。可见在研究频段内,起主要贡献作用的只有F0波,可得共振频率的预报公式为
式中,β表示图11 中OC1与OD1之间的夹角。将预报结果添加至辐射声压的频率-充液高度谱中,结果如图18所示。

图18 流体附加波共振预报结果与数值计算结果对比Fig.18 Comparison of prediction results and numerical calculation results of fluid additional wave resonance
图中红色曲线即为F0波共振的预报结果。由频散曲线易知,F0波相速度在研究频段内几乎不变,表现在辐射声压的频率-充液高度谱中为近似线性分布,吻合得很好。说明了本章推导的预报公式能准确地预报辐射声压的频率-充液高度谱中的共振现象,同时解释了流体附加波对壳体辐射声场的影响规律。
4 结 论
本文分析了部分浸没圆柱壳和部分充液圆柱壳辐射声场的构成,利用有限元软件建立了部分浸没半充液无限长圆柱壳和半浸没部分充液无限长圆柱壳辐射的仿真模型,基于COMSOL 软件计算得到辐射声压的频率-浸没深度/充液高度谱。通过壳体中各种波的相速度频散曲线解释了辐射声场中呈现的辐射共振现象。得到如下结论:
(1)部分浸没半充液无限长圆柱壳和半浸没部分充液无限长圆柱壳辐射声场均呈现出一系列规律分布的共振峰,这是由于壳体中弯曲波a0在不同部分的传播速度不同导致的;
(2)部分浸没半充液圆柱壳的辐射声场中存在的独立分布的共振峰,是由壳体内低阶流体附加环绕波F0和F1激发的,其分布规律与壳体浸没深度有关;
(3)半浸没部分充液圆柱壳的辐射声场中存在的独立共振峰则主要由F0波贡献,在壳体辐射的频率-充液高度谱中近似呈现线性分布规律;
(4)基于壳体中各种波的相速度频散曲线推导出的频率预报公式能够准确地预报声场中出现的共振现象;
(5)经过验证,当壳体的厚径比改变时,共振频点间隔随之改变,但是分布规律以及产生的机理相同,因此本文结论具有普适性。
